颗粒材料在自然界中极其普遍,一般分为粉体和散体,它的力学特征可概括为“散”和“动”。“散”指颗粒形状的分散性;“动”指颗粒凝聚、聚团的破裂、破碎等。

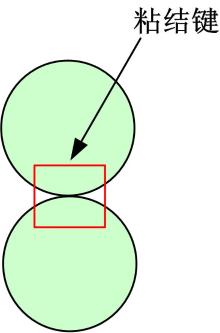
食物块可以视为一种颗粒材料,它是由大量排列紧密的离散的微颗粒组成的,微颗粒是最小的单元。用离散元法对食物块进行分析时,认为微颗粒之间是相互粘结在一起的,利用bonding模型使微颗粒粘结成一个完整的食物块大颗粒。组成食物块的微颗粒是可产生线性变形的弹性体,用离散元法研究食物块时选用软球模型,颗粒之间存在叠合量。在三维空间中,微颗粒是随机排列的,每个微颗粒可能会与周围的26个微颗粒粘结,两个微颗粒的接触点处存在粘结键,如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 微颗粒之间的粘结Fig.1 Bonding between the micro particles

当边界运动时,微颗粒受到压缩力、剪切力等作用,互相之间还存在碰撞、摩擦作用,描述微颗粒的受力以及微颗粒之间的作用力需要知道微颗粒的一些本构参数:密度、泊松比、剪切模量、碰撞恢复因数、静摩擦因数、滚动摩擦因数。微颗粒相当于食物块大颗粒的一个分支,测定食物块中微颗粒的这些本构参数时,以大颗粒的本构参数测定结果为准。

利用牙齿进行咀嚼运动时,上下第一磨牙在咬合时起主要作用,咬合的运动规律非常复杂,本文将咬合运动简化为匀速运动模式,即上磨牙不动,下磨牙以恒定的速度向上逐渐挤压食物块。咀嚼过程中,食物块与上下磨牙会有接触,牙齿作为边界,施加作用力于食物块,二者均受力。

若要分析食物块中的微颗粒与牙齿的接触作用力,必须首先确定与微颗粒接触的边界,即进行接触判断。将分析空间(包括牙齿和食物块)划分成规则的网格,对于组成食物块的每一个微颗粒来说,其所在的网格及其邻接网格内的边界可作为该微颗粒的邻居边界,其他任何单元的扰动都不能传递过来,只需要检查该微颗粒是否与邻居边界接触。完成接触判断之后,就可以计算出每个时刻食物块与牙齿边界的作用力。

利用Bonding模型描述食物块与牙齿之间的接触,随着牙齿的咀嚼运动,食物块与牙齿之间会发生碰撞、摩擦等现象,原有接触关系被不断改变,需要确定如下的参数:微颗粒与牙齿之间的碰撞恢复因数、静摩擦因数、滚动摩擦因数。测定这些参数时,以大颗粒代替微颗粒进行测定。

1.3.1 咀嚼破碎模型的基本流程

离散元法描述的是颗粒之间以及颗粒与边界之间的碰撞过程,也就是接触的产生和分离的过程,由此可以进行碰撞过程中的力学性能分析。

为了用离散元的方法模拟咀嚼破碎过程,提出了咀嚼破碎模型,实现该模型的核心是将原始的食物大颗粒替换成颗粒簇。首先定义一个食物块大颗粒,在某一个时间点,将这个大颗粒用一个颗粒体积力移出计算域;然后记录这个大颗粒原来所在的位置信息,并且以这个位置信息为中心点,在周围紧密生成一群粒径相等的微颗粒,每个微颗粒的位置信息必须在替换之前计算好;替换后,利用Bonding模型触发,任意两个微颗粒之间迅速发生粘结作用,产生粘结键,形成颗粒簇;然后下颔匀速向上挤压微颗粒组成的食物块,食物块受到剪切力、压缩力等作用,当微颗粒之间的法向应力和切向应力超过临界值时,粘结键失效,颗粒簇开始破碎。咀嚼破碎模型的基本流程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 咀嚼破碎模型流程图Fig.2 Flow chart of chewing broken model

一个由微颗粒组成的食物大颗粒在咀嚼过程中,粘结的微颗粒数目逐渐减少,失效的粘结键越来越多,咀嚼1次、2次、3次,…, n次之后,X-Y平面内粘结键被破坏的效果图如图3所示,假设食物块形状为长方体,图中线条表示被破坏的粘结键,咀嚼n次之后所有的粘结键均失效。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 粘结键破坏效果图Fig.3 Damage effect of bonding key

1.3.2 颗粒簇位置信息的获取

将食物颗粒替换成颗粒簇之前,需要计算出颗粒簇中每个微颗粒的位置信息。

首先求得微颗粒的数目。将初始食物大颗粒用Whole表示,颗粒簇中的微颗粒用Fraction表示。由于Fraction之间是相切的,这里将大颗粒Whole的填充体积分数取为0.56。

0.56·VWhole=N·VFractionn1

式中: VWhole为大颗粒的体积; VFractionn为破碎后的微颗粒体积;N为微颗粒Fraction的个数。

求得微颗粒Fraction的数目 N之后,利用离散元的方法模拟两个几何体挤压成一个Whole颗粒的过程。利用三维作图软件Catia生成两个大小一致、方向相反的两个曲面模型,二者以相同的速度相对运动,挤压成一个Whole颗粒大小的空间,空间内部生成 N个微颗粒Fraction,正好将这个空间填充满。挤压之后的示意图如图4所示,可以得到 N个微颗粒Fraction的三维坐标信息,形成数据文件。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 颗粒簇位置信息的获取Fig.4 Retrieval of particle cluster location information

用离散元法分析食物块在咀嚼过程中的受力,将食物块视为颗粒,需要赋予颗粒一些参数。

以大豆为例,从超市购买上仓杂粮家族的有机大豆若干(含水率约为13.99%)。

大豆密度 ρ由质量与体积的比值求得。从购买的大豆中分3次随机取出1000粒种子,用电子分析天平测得其千粒重,取3次的平均值。通过测得大豆的三维尺寸,计算出球形率^{[ 8]},发现大豆的球形率超过92%,因此在离散元分析时,将大豆的几何形状近似为球形,并将其假设为均质的且各向同性,再根据三维尺寸计算出等效直径^{[ 8]}。

大豆的泊松比用 λ表示,一般取经验值0.4^{[ 9]},在0.4附近取5个不同的泊松比,分析大豆颗粒受到的力是否变化。利用离散元的方法模拟质构仪探头垂直向下压缩大豆颗粒,泊松比分别取0.36、0.38、0.4、0.42、0.44,颗粒的其他参数值不变,边界向下运动的速度设为定值。每种情况模拟10次,取平均值,图5为颗粒受到的压力随泊松比变化的趋势。该图说明用离散元模拟压缩过程时,泊松比对其结果影响不大。这里将泊松比取经验值0.4。

图5

Fig.5

	Figure Option '>ViewDownloadNew Window
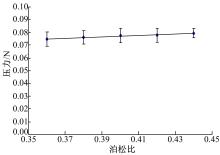'>	图5 压力随泊松比的变化趋势图Fig.5 Curves of poisson's ratio and load

大豆颗粒的剪切模量用 G表示:

G=E2(1+λ)2

式中: E为弹性模量,具体测量方法见文献[10],测量10次,取平均值。

大豆颗粒之间的碰撞恢复系数 e由高速视频摄像系统和自制跌落仪测得^{[ 11]},将大豆单侧粘合在测试平台上,以粘合形成的密集排布的大豆面作为摩擦表面,从30 cm的高度使一粒大豆跌落到摩擦表面,用高速摄像系统采集到大豆弹起的最高点,读出对应的刻度值,见图6。测量10次,取平均值。

e=h/H3

式中: h为弹起的最高点高度, H=30 cm。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 碰撞恢复系数的测试Fig.6 Test of restitution coefficient

大豆颗粒之间静摩擦因数 μ利用静摩擦因数测试装置测得^{[ 12]},见图7。将大豆单侧粘合在测试斜面上,以粘合形成的密集排布的大豆面作为摩擦表面,再把需要测定的大豆样品放在摩擦表面上(保证其不滑落),然后将斜面的倾斜角度 θ慢慢调大,当大豆开始在斜面上产生滑移时,大豆受到的力是最大静摩擦力,计算出斜面和水平面的夹角 θ,静摩擦因数 μ=tanθ。测量10次,取平均值。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 静摩擦因数测试装置Fig.7 Test of the coefficient of static friction

颗粒的摩擦因数与颗粒堆积的休止角有关^{[ 13]}。这里大豆颗粒间滚动摩擦因数 σ是利用离散元模拟颗粒堆积得到,具体方法是:在小漏斗上面的指定区域生成大豆颗粒群,颗粒群在重力作用下自由下落,缓慢提升小漏斗,使大豆颗粒缓慢流出,并堆积成堆。用量尺量出堆积角的大小,若小于真实情况的堆积角,就把滚动摩擦因数调大一些,相反调小一些,每次调整幅度为0.002,经过多次试算确定大豆的滚动摩擦因数,确保与真实堆积角的误差在±5%之间。图8为模拟大豆颗粒堆积示意图。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 模拟颗粒堆积Fig.8 Simulation of particle accumulation

大豆本构参数如下:泊松比 λ为0.4,剪切模量 G为7.1×10⁶ Pa,密度 ρ为1149 kg·m^-3,颗粒间碰撞恢复系数 e为0.356,颗粒间静摩擦因数 μ为0.403,颗粒间滚动摩擦因数 σ为0.424。

利用美国GE公司制造的Lightspeed 16层螺旋CT扫描机,获得人牙齿的二维CT图像资料,将其导入医用图像合成处理软件Mimics,进行前处理,再利用逆向工程软件Geomagic studio对点云进行滤波、删减、修补等处理,将修复完整的点云封装成多边形,再对多边形进行修补、平滑处理,划分曲面栅格,使用曲面拟合方法重构出牙颔的三维模型。同时调整好上、下颔的位置,遵循“杵-臼”模型^{[ 14]},得到重建后的牙齿三维模型。图9为牙齿三维模型。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 牙齿三维模型Fig.9 Three-dimension teeth models

人牙本质的弹性模量取18.6 GPa,泊松比取0.31^{[ 15]},密度为3.98 g/c m316。

聚乙烯纤维树脂材料与人牙弹性模量最接近^{[ 17]},选取一块10 cm×10 cm大小的聚乙烯纤维树脂复合板来测定大豆颗粒与牙齿齿面之间的碰撞恢复系数 e1、静摩擦因数 μ1、滚动摩擦因数 σ1,测试方法与2.1节相同。

大豆颗粒与边界之间的滚动摩擦因数 σ1用WCT32F微型摩擦试验机测得^{[ 12]}。选取量程为10 kg的力传感器和往复直线运动的测试模式,设置相应的参数,包括法向力-15 N、运动速度6000 mm/min、摩擦时间30 s。重复测试10次,取平均值作为样品的滚动摩擦因数。

大豆颗粒与边界之间的参数如下:碰撞恢复系数 e1为0.523,静摩擦因数 μ1为0.364,滚动摩擦因数 σ1为0.394。

2.3.1 破碎粒径的选取

以大豆(含水率约为13.99%)为例,用筛分法确定咀嚼破碎模型破碎后微颗粒的粒径。

咀嚼效果一般用食物的破碎率来衡量,破碎率用粒径小于2 mm的颗粒质量百分比来表征^{[ 14]}。破碎率达到90%以上时,就认为达到了可吞咽的程度。

按照感官评定试验的标准筛选出咀嚼功能正常、有一定分辨能力的感官鉴评人员30名,对他们进行咀嚼训练,男女各15人,然后按正常咀嚼速度分别对大豆咀嚼5、10、15、20次。

采用筛分法对咀嚼之后的破碎颗粒进行粒径统计。咀嚼时,唾液会使破碎颗粒粘结在一起,形成食物团,不便于测量其粒径,因此在筛分之前,用超声波振荡法使其分散,超声波功率为100 W,振荡20 min。分散之后,将样品置于52 ℃的烘箱中静止烘干2 h。选择一系列不同孔径的标准筛,依次摞起,从上到下分别为5目(4 mm)、6目(3.35 mm)、10目(2 mm)、12目(1.7 mm)、16目(1.18 mm)、20目(0.85 mm),手动筛分得到破碎后颗粒的质量分数。20次咀嚼循环之后的大豆样品可以筛分出4种粒径:10目筛的筛上物粒径约为3 mm,12目筛的筛上物粒径约为1.8 mm,16目筛的筛上物粒径约为1.4 mm,20目筛的筛上物粒径约为1 mm,对这4种颗粒进行称重,得到质量分数,在图10中体现。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 咀嚼后粒径质量分数Fig.10 Particle size percentage after chewing

图10的结果显示,粒径小于2 mm的颗粒质量分数为96.28%,即大豆的破碎率达到了90%以上,咀嚼20次可以吞咽。

大豆被视为一种由微颗粒组成的颗粒聚团,将咀嚼至可吞咽程度(即咀嚼20次)时筛分出的最小粒径当作组成大豆的微颗粒Fraction的粒径,后续模拟大豆咀嚼过程时选取颗粒簇的粒径为1 mm。

2.3.2 粘结参数的选取

当大颗粒被颗粒簇替换后,发生粘结作用,需要设置5个粘结参数:粘结半径、法向刚度、切向刚度、法向最大应力、切向最大应力。

颗粒簇在指定的粘结时刻发生粘结,在此之前,颗粒之间遵循默认的接触模型。粘结之后,颗粒之间遵循Bonding模型,力和力矩首先归0,每个时间步的法向力、切向力、法向力矩、切向力矩逐步叠加。当法向应力和切向应力达到预先设置的最大值时,颗粒之间的粘结键被破坏。

粘结半径 r一般等于微颗粒Fraction的半径。大豆的法向刚度 kn利用WDW-20J电子万能试验机测得^{[ 11]},大豆颗粒平放,重复测量10次,取平均值。切向刚度 kt一般取法向刚度 kn的2/3~1倍^{[ 18]},这里切向刚度取法向刚度的0.8倍。

法向最大应力和切向最大应力按照下面的公式求得:

F'n=kn·2r4F't=kt·2r5σmax=-F'nπr26τmax=-F'tπr27

式中: F'n为法向最大力; F't为切向最大力; σmax为法向最大应力; τmax为切向最大应力。

粘结参数的具体取值如下:粘结半径 r为0.5 mm,法向刚度 kn为290 000 N/m,切向刚度 kt为232 000 N/m,法向最大应力 σmax为3.7×10⁸ Pa,切向最大应力 τmax为3×10⁸ Pa。

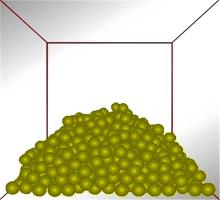
咀嚼破碎模型提供一个很大的体积力将大颗粒移出指定区域,然后生成一堆粒径相等的微颗粒,微颗粒在生成的时候会向上碰撞边界,若颗粒的剪切模量过大,会产生极大的反弹力,微颗粒之间无法实现粘结,产生爆炸现象,如图11所示。将剪切模量缩小可以解决这一问题,这里选取大豆的剪切模量比真实值小1000倍。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 颗粒爆炸现象Fig.11 Phenomenon of particles explosion

剪切模量缩小之后,仿真结果需要进行修正,仿真得到的食物块受到的压力与试验测得的压力存在如下关系:

Ys=kYt+b8

式中: Ys为离散元仿真结果; Yt为试验测得结果; k为修正系数;b为常数。

用离散元模拟大豆的咀嚼过程时,咬合运动简化为匀速运动,上颔固定不动,下颔以一定的速度向上垂直运动一次,再回到初始位置相当于一个咀嚼周期。将大豆颗粒替换成颗粒簇的替换时间设置为0.195 s,粘结时间设置为0.196 s,微颗粒Fraction的接触半径大于微颗粒自身半径的25%,下颔运动速度设置为2 mm/s^{[ 19]},位移3 mm,时间步长取1×10^-6 s,网格尺寸为微颗粒半径的3倍,咀嚼3个周期。

将颗粒工厂设置成位于第一上、下磨牙之间,在其内静态生成一个大豆颗粒,颗粒工厂体积不能小于颗粒体积,由于人在用磨牙咀嚼时大豆颗粒的位置是随机放置的,因此这里将颗粒生成位置设定为随机生成。

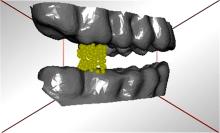
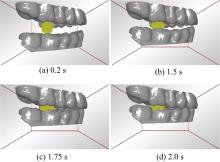
大颗粒被替换成颗粒簇之后,微颗粒之间迅速发生粘结,如图12(a)。下颔继续向上运动时,挤压大豆,当任意两个微颗粒之间的法向应力和切向应力超过最大极限值时,颗粒簇开始破碎,如图12(b)(c)(d)。达到预设的时间之后下颔向下运动回到初始位置,如此循环咀嚼3个周期。将所有微颗粒受到的压力和记为大豆颗粒受到的压力。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 咀嚼过程动态仿真Fig.12 Dynamic simulation of chewing process

图13为对大豆样品咀嚼3个周期的压力信号随时间变化的曲线。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 仿真结果Fig.13 DEM simulation results

利用逆向工程技术建立了人类第一上、下磨牙的三维模型,研制了齿形压头,压头采用仿生材料,尺寸与第一磨牙近似,在压头的根部底面中心加工螺纹,以便安装在质地测试仪器上。将齿形压头安装在CT3质构仪上,对大豆(含水率为13.99%)进行破碎,第一下磨牙安装在质构仪上,第一上磨牙置于底座上,上、下磨牙按照“杵-臼”模型^{[ 14]}规律配合放置,如图14所示。

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 齿形压头Fig.14 Dentiform indenter

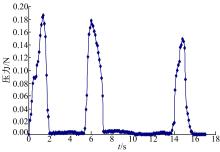
质构仪压缩速度为匀速,设置为2 mm/s,与仿真时咬合的速度一致;目标位移为3 mm;触发点负载设置为1 N;压缩模式为循环3次,每隔0.2 s记录数据。得到样品受到的压力随时间的变化曲线如图15所示。

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 齿形压头测试曲线Fig.15 Test curves of dentiform indenter

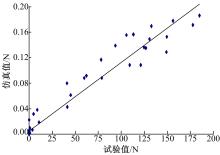
从图15可以看出:质构仪配合齿形压头压缩3次的压力变化趋势与咀嚼破碎模型咀嚼3个周期的压力变化趋势一致。对质构仪试验得到的压力值与仿真得到的压力值做一元线性回归,式(8)中修正系数 k=0.0011,b=0.005,复相关系数R为0.978,判定系数R2为0.956,回归方程的估计标准误差为0.011 952,回归方程显著性检验的概率值为0.000,试验值与仿真值的对比如图16所示。对样品进行重复试验,结果无显著差异。

图16

Fig.16

	Figure Option ViewDownloadNew Window
	图16 仿真值与试验值对比Fig.16 Comparison of simulation results and experiment results

分析表明,利用咀嚼破碎模型仿真得到的结果经过以上一元线性回归模型的修正后,能够直接分析出咀嚼过程中食物块的受力情况。