基于局部搜索和整体优化的客车杆件截面参数正向设计

引用本文

那景新, 高剑峰. 基于局部搜索和整体优化的客车杆件截面参数正向设计. 44(6): 1564-1570
NA Jing-xin, GAO Jian-feng. Top-down design method based on local search and global optimization for cross-sectional size of bus body. Journal of Jilin University Engineering and Technology Edition, 44(6): 1564-1570 复制到剪切板

Permissions

基于局部搜索和整体优化的客车杆件截面参数正向设计

那景新, 高剑峰

吉林大学汽车仿真与控制国家重点实验室,长春 130022

作者简介:那景新(1957-),男,教授,博士生导师.研究方向:汽车设计理论与轻量化技术.E-mail:najx@jlu.edu.cn

基金:国家自然科学基金项目(51075187);

摘要

首先建立了局部一维搜索方法,以客车车身线框模型与型钢截面库为基础,通过截面库优化排序、杆件局部模型一维搜索以及局部-整体迭代等优化步骤,得出一个满足多工况强度要求的车身结构杆件截面尺寸下限。然后通过灵敏度分析选择关键杆件,利用多目标遗传算法NSGA-II对选定杆件的截面尺寸在截面库的范围内进行优化,以提高整体刚度及模态性能。最后在某承载式客车车身杆件截面优化设计中,将该方法的优化结果作为设计输入,结果表明,车身结构的最终方案具有明显的轻量化效果。

关键词: 车辆工程; 客车车身; 正向设计; 截面优化; 一维搜索; 多目标遗传算法

中图分类号:U463.82 文献标志码:A 文章编号:1671-5497(2014)06-1564-07

Top-down design method based on local search and global optimization for cross-sectional size of bus body

NA Jing-xin, GAO Jian-feng

State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

Abstract

In this paper, first, the lightest structure under the strength condition was obtained via the implementation of strength optimization based on the wire-frame model of body structure and the sectional library. Sequencing optimization of the sectional library, local line search and local-global iterative process were contained in the strength optimization. Second, sensitivity analysis was carried out to select design variables, which are more sensitive to the stiffness and modal frequency of the body structure. Finally, the selected variables were optimized within the limits of sectional library to improve the performance of the body stiffness and modal frequency using the multi-objective genetic algorithm NSGA-II. This approach was implemented into the design process of an integral bus body. The results indicate that the proposed sectional optimization method is efficient and conducive to light-weighting of bus bodies.

Keyword: vehicle engineering; bus body; top-down design; sectional optimization; line search; multi-objective genetic algorithm

Show Figures

0 引言

随着对公路客车结构安全性及轻量化要求的不断提高,国内的客车正在经历由半承载式结构向全承载式结构过渡的重要阶段。与半承载式车身结构主要依靠车架大截面纵梁弯曲承载不同,全承载式车身结构的承载主体是由多根细长的小截面杆件所组成的“笼式”结构,若设计合理,就可以充分发挥细长杆件承受轴向载荷能力强的特点,尽可能地将车身上的工作载荷分解为各杆件上的轴向载荷。因此,与同等质量的半承载式车身结构相比,全承载式客车的车身骨架结构在某些性能上(例如车身刚度、侧翻安全性等)具有显著的优势^{[ 1, 2]}。

许多学者就如何提高车身结构整体性能(如刚度、模态等)进行了研究,诸如遗传算法等各类智能算法被引入到车身结构的优化中,取得了许多成果^{[ 3, 4, 5]}。但由于客车车身结构杆件数量往往数以百计,若将所有杆件截面均作为轻量化的优化对象,智能算法求解时间较长。因此,实际应用中通常通过灵敏度分析选择少部分关键车身杆件进行针对性的优化。研究证明:关键杆件的改善能够有效地提高车身刚度及模态特性^{[ 6, 7, 8]}。但在实际工程中,由于承载式客车的强度性能比刚度性能更容易出现问题^{[ 9]},为了保证车身结构具有足够的强度性能,设计人员在杆件的断面设计时多根据经验采取保守设计,因此产生的结构往往强度过剩,轻量化程度有限。因此,若能建立一种优化设计方法,先根据每根杆件的强度要求设计杆件截面尺寸,再利用智能算法对关键杆件进行优化以提高车身整体性能,就能进一步地减少因为保守设计所产生的多余质量,提高车身结构的轻量化程度。

基于上述分析,本文将局部搜索与整体优化相结合,建立车身杆件截面参数的正向设计方法。该方法以概念设计阶段的车身线框模型以及符合实际工程要求的型钢截面库为基础,首先对型钢截面库中的截面进行优化排序。然后通过局部一维搜索方法,对车身结构所有杆件进行截面尺寸的搜索优化,快速找到满足多工况强度要求的最轻车身结构方案;在此基础上通过灵敏度分析选择关键杆件作为整体性能的优化变量,利用多目标遗传算法NSGA-II对车身结构进行多目标优化,使车身整体刚度和模态性能达到目标要求。

1 杆件截面优化设计方法

强度是局部约束问题,可以通过局部分析快速求解;刚度和模态是结构的整体约束问题,需要在整体模型中分析求解。采用智能算法对整体约束问题迭代求解所需要的时间随着优化变量的增加呈几何级数上升,因此实际应用中通常选择少部分关键杆件的截面尺寸作为优化变量进行优化。在改善车身性能的同时,为了尽可能地提高车身结构的轻量化程度,本文建立了一种两级优化的方法:第一级优化中,建立局部一维搜索优化方法,对车身所有杆件的强度性能进行快速的局部搜索优化,将优化结果作为整体性能优化的强度下限;当强度优化获得的结构不满足刚度或模态等整体性能时,进行第二级优化,采用多目标遗传算法对一些选定的关键杆件进行截面尺寸加强,以提高车身各项整体性能。相比第二级整体优化,第一级局部搜索的变量范围广(所有的车身杆件),能够快速有效地提高车身结构的轻量化程度。

1.1 型钢截面库

对杆件截面进行优化设计之前,根据企业提供的型钢规格列表为车身结构各杆件建立截面库。初始截面库所包含截面类型相同的标件数量是相同的。截面库中主要包含了工程中常见的矩形断面,因为承载式客车车身结构中绝大多数承载杆件均为矩形型钢,如槽形梁、L型梁等。异形断面杆件更多是作为功能件存在,如用于固定油箱、固定座椅等。

截面库中包含了各截面的主要物理参数,即 x⁽ ⁱ⁾ ={ b⁽ ⁱ⁾, h⁽ ⁱ⁾, t⁽ ⁱ⁾, A⁽ ⁱ⁾, $\begin{matrix} {I_{y}}^{(i)} \end{matrix}$ , $\begin{matrix} {I_{z}}^{(i)} \end{matrix}$ },上标( i)表示杆件编号。 A⁽ ⁱ⁾为杆件 i的横截面积; h⁽ ⁱ⁾为杆件 i的截面高度; b⁽ ⁱ⁾为杆件 i的截面宽度; t⁽ ⁱ⁾为杆件 i的截面厚度; $\begin{matrix} I_{y}^{(i)} \end{matrix}$ 、 $\begin{matrix} I_{z}^{(i)} \end{matrix}$ 分别为杆件 i截面上沿局部坐标系 y轴和 z轴的抗弯模量。对于杆件 i,其对应的截面库记为 S⁽ ⁱ⁾,包含了变量 x⁽ ⁱ⁾的 p个取值集合,即 $\begin{matrix} x_{j}^{(i)} \end{matrix}$ ∈ S⁽ ⁱ⁾, j=1,2,…, p。矩形型钢的断面坐标系和尺寸定义如图1所示。

	Figure Option View Download New Window
	图1 矩形型钢截面Fig.1 Rectangular cross-section of profile steel

1.2 局部一维搜索方法

应力优化设计的数学模型为:

$\begin{matrix} \{\begin{matrix} \min W = \overset{n}{\sum_{i = 1}} ρ A^{(i)} L^{(i)} \\ s . t . σ_{\max}^{(i)} - [σ] \leq 0, i = 1,2, \dots, n \end{matrix} (1) \end{matrix}$

式中: W为车身质量; ρ为材料密度; L⁽ ⁱ⁾为杆件 i的长度; $\begin{matrix} σ_{\max}^{(i)} \end{matrix}$ 为杆件 i的最大应力; n为杆件数量。

有限元模型中,杆件 i被划分成 m个梁单元,根据材料力学理论,断面 k的最大等效应力为:

$\begin{matrix} σ_{k}^{(i)} = \frac{F^{(i)}}{A^{(i)}} + \frac{M_{y}_{k}^{(i)} \cdot h^{(i)}}{2 I_{y}^{(i)}} + \frac{{M_{zk}}^{(i)} \cdot b^{(i)}}{2 I_{z}^{(i)}} (2) \end{matrix}$

式中: F⁽ ⁱ⁾为杆件 i所受轴向力; $\begin{matrix} M_{y}_{k}^{(i)} \end{matrix}$ 为截平面坐标系 y方向上截面 k处所受的弯矩; $\begin{matrix} {M_{zk}}^{(i)} \end{matrix}$ 为截平面坐标系 z方向上截面 k处所受的弯矩。杆件 i的最大应力为 $\begin{matrix} σ_{\max}^{(i)} \end{matrix}$ =max{ $\begin{matrix} σ_{1}^{(i)} \end{matrix}$ , $\begin{matrix} σ_{2}^{(i)} \end{matrix}$ ,…, $\begin{matrix} σ_{m + 1}^{(i)} \end{matrix}$ }。

在强度工况下,对车身结构作暂时的静定化假设——假定各杆件内力不会随着杆件截面的改变而改变。在这种假设下,强度约束(应力约束)属于局部约束,各杆件应力计算结果只与杆件本身的截面尺寸参数有关。因此,可以通过建立杆件局部模型以取代整体模型进行优化求解。根据一维搜索的思想,将各型钢截面库按照型钢截面积升序排列,从排序后的第一个型钢开始,依次将该型钢的各项参数变量代入约束条件,若约束条件不满足,检查下一个型钢,直到满足约束条件为止。这样就从各杆件的截面库中筛选出了满足强度条件的最轻结构。

实际上,客车车身骨架这样的超静定结构,杆件断面的变化一般都会引起内力重分布,因此各杆件的满足强度条件的最轻结构还需放入整体结构中进行重复迭代,直至收敛。同时,考虑到客车骨架的实际生产工艺中对称性(即车身左右两侧结构基本对称)及统一性(例如车窗立柱,由于不同立柱的弧度、长度等基本相同,为避免焊接错误,通常要求这些杆件的截面尺寸保持一致)对提高生产效率的重要性,在优化搜索过程中,考虑以上要求,保持相关杆件截面属性的一致性。

局部模型一维搜索的具体步骤如下:

(1)对车身线框模型进行网格划分,建立车身结构梁单元模型。

(2)对车身梁单元模型进行分组,分组过程中考虑实际生产中的对称性及统一性,处于同一组中的杆件将使用同一个截面库。

(3)将截面库 S⁽ ⁱ⁾按照杆件截面积 A⁽ ⁱ⁾升序排列。

(4)将车身各杆件截面初始化为对应的截面库中的第一个截面,即 $\begin{matrix} x_{j}^{(i)} \end{matrix}$ ( j=1, i=1,2,…, n),此时车身结构显然是最轻的,但不满足强度要求。

(5)将车身结构放入各强度工况中(包括满载弯曲工况、左前轮悬空工况及右前轮悬空工况等)进行应力分析,判断各杆件所对应的最危险工况并提取各杆件在最危险工况下的杆件内力。

(6)根据应力分析结果,选出所有不满足强度条件的杆件组,按截面库中的顺序选择下一个型钢截面 $\begin{matrix} x_{j + 1}^{(i)} \end{matrix}$ ,并将该截面所包含的尺寸信息代入约束条件( $\begin{matrix} σ_{\max}^{(i)} \end{matrix}$ -[ σ]≤0),若不满足则检查下一个型钢,直到满足约束条件为止。

(7)由于杆件截面发生变化结构内力将重新分配,因此将局部搜索获得的解代入有限元模型进行强度计算,获得重分配后的杆件内力。

(8)重复步骤(5)~(7),直至结果收敛。

根据目标函数和约束函数的单调性质,此时求得的解是满足强度条件的最轻结构。利用局部模型求解应力约束,可以快速排除不满足强度约束条件的解,为后续的优化设计提供各变量的强度下限。

车身结构的强度分析由MSC.NASTRAN求解,其余子程序由FORTRAN实现,包括截面库排序、单元信息提取与统计、局部模型应力重分析,更新求解器输入文件等。

1.3 灵敏度分析

在第二级优化中,计算代价相比第一级优化大大增加,优化变量从所有的杆件变为少部分关键杆件。考虑轻量化和目标性能的要求,定义如下3个相对灵敏度系数:

$\begin{matrix} \begin{matrix} BW = \frac{Δ K_{B}}{ΔW} (3) \\ TW = \frac{Δ K_{T}}{ΔW} (4) \\ MW = \frac{Δ f_{T}}{ΔW} (5) \end{matrix} \end{matrix}$

式中: ΔK_B、 ΔK_T、 Δf_T分别为设计变量改变所引起的弯曲刚度、扭转刚度和一阶扭转频率改变量; ΔW为设计变量改变所引起的质量改变量。

1.4 多目标优化

在强度优化的基础上进行车身整体性能的优化,包括一阶扭转模态、扭转刚度及弯曲刚度,优化问题数学模型如下:

$\begin{matrix} \{\begin{matrix} \min {W (x), - K_{B} (x), - K_{T} (x), - f_{T} (x)} \\ s . t . σ_{\max} (x) - [σ] \leq 0 \\ x_{l} < x < x_{u} \end{matrix} (6) \end{matrix}$

式中: σ_max( x)为车身结构在多种强度工况下的最大应力;[ σ]为车身材料屈服极限; K_B( x)为车身弯曲刚度; K_T( x)为车身扭转刚度; f_T( x)为车身一阶扭转模态频率值, x=[ x₁, x₂,…, x_n]^T为设计变量向量; x_l、 x_u分别为 x的上、下限,且 x_l由第一轮优化获得。

本文所采用的多目标算法为NSGA-II,是Kalyanmoy等^{[ 10]}于2002年提出的一种基于快速非支配排序方法的多目标遗传算法。由于良好的分布性和快速收敛的特点,该方法已经在工程中得到了成功的应用^{[ 11, 12, 13]}。该算法流程如下:

(1)随机产生规模为 N的初始种群 P_t( t=0),对初始种群进行非支配性排序。

(2)对排序后的初始种群执行选择、交叉及变异操作,产生种群规模为 N的子代 Q_t。

(3)合并父代和子代,产生规模为2 N的新种群 R_t=P_t∪ Q_t,同时对新种群进行非支配性排序,获得非支配前端 F₁, F₂,…。

(4)计算每个个体在其所处于的非支配前端等级上的拥挤度,进行拥挤比较操作,选择种群 R_t中最好的 N个个体组成下一代父种群 P_t+₁。

(5)对父种群 P_t+₁进行选择、交叉及变异操作,形成子代 Q_t+₁。

(6)重复上述步骤,直至终止条件满足。

在这个两级优化的方法中,第一级优化的变量(车身所有杆件)完全包含第二级优化的变量(关键杆件),第二级优化只覆盖第一级的少部分优化结果,第一级优化产生的轻量化效果仍然是可观的。

2 应用实例

2.1 有限元模型及试验验证

本文选取某12 m承载式公路客车在概念设计阶段的车身线框结构作为研究对象。图2为该结构方案的三维线框示意图。

	Figure Option View Download New Window
	图2 车身骨架线框示意图Fig.2 Wireframe of body structure

在概念设计阶段,对样车进行有限元模型的验证是比较困难的。因此选取该车身结构的对标车型进行应力测试,以验证本文建模方法的有效性。对标车型车身结构同样采用梁单元与壳单元混合建模,测试载荷为乘员舱地板平面上的25000 N均布载荷,在对标车型的车身骨架上选取25个测点获取测试应力值。

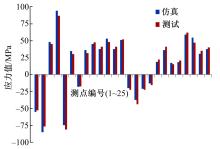
图3为对标车型的应力测试现场; 图4为测点应力值与模拟应力值的对比图。

	Figure Option View Download New Window
	图3 对标车型应力测试Fig.3 Scene of the test to target bus body

	Figure Option View Download New Window
	图4 测点应力值与模拟应力值对比图Fig.4 Stress values of test points from test data and simulation data

与试验测试结果相比,最大仿真误差为15.48%,平均误差为9.91%。这表明有限元模型的建模方法是可靠的,能够反映车身结构在选定载荷下的应力分布情况。对标车型主要性能指标为一阶扭转频率7.81 Hz;弯曲刚度1.05×10⁷ N·m·rad^-1;扭转刚度4.27×10⁴ N·m·deg^-1;车身质量2848 kg。

2.2 CAE驱动的杆件截面正向设计

在应用中,车身骨架采用梁单元进行有限元建模,部分加强板结构以壳单元进行模拟。整体模型共有9024个梁单元,3498个壳单元。建立型钢截面库,并将车身所有杆件截面初始化(定义为截面库中断面积最小的截面),模型如图5所示。

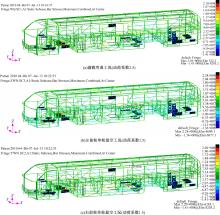
定义应力约束条件,对此初始结构进行一维搜索优化。经过8轮迭代后结果收敛,获得满足强度条件的最轻车身结构,车身骨架质量为2309 kg。图6为该车身结构在3种典型强度工况下的应力情况;该车身结构的各项指标为:一阶扭转频率7.76 Hz;弯曲刚度9.37×10⁶ N·m; 扭转刚度4.41×10⁴ Nm· deg^-1;车身质量2309 kg。

	Figure Option View Download New Window
	图5 车身整体有限元模型Fig.5 FE model of body structure

	Figure Option View Download New Window
	图6 三种典型工况下车身应力云图Fig.6 Stress distribution of body structure under 3 typical conditions

采用灵敏度分析方法,选择车身上对弯曲刚度、扭转刚度及一阶扭转模态贡献较大的杆件共63根,如图7中浅色部分所示。对所选定杆件的截面尺寸参数进行多目标优化,设定种群大小为100,迭代次数为200。通过NSGA-II获得的Pateto解的集合如表1所示。

	Figure Option View Download New Window
	图7 灵敏度较高杆件分布示意图Fig.7 Components of the bus body related to the sensitivity analysis

表1 多目标优化方案列表 Table 1 Pareto solutions obtained by NSGA-II

综合各项目标性能,选择方案19作为车身杆件截面尺寸的最终方案。从优化结果上看,车身各项主要性能明显高于目标车型,且车身质量与目标车型相比轻了10.6%。

3 结束语

建立了一种局部搜索与整体优化相结合的客车骨架杆件截面参数正向设计方法,包括基于应力的局部一维搜索优化以及车身整体性能优化两部分。并将该方法应用于某承载式客车车身杆件截面尺寸的设计中。结果表明,采用该方法所建立的车身结构方案,轻量化效果明显,能够为后续设计提供参考;强度优化中所有的搜索优化过程均在局部杆件模型中进行,计算速度快、计算代价低;该设计方法的整个过程均基于实际的型钢截面库进行,优化结果符合工程要求,具有较好的工程应用价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	刘江, 桂良进, 王青春, 等. 全承载式大客车车身结构多目标优化[J]. 汽车工程, 2008, 30(2): 170-173. Liu Jiang, Gui Liang-jin, Wang Qing-chun, et al. Multi-objective optimization on the body structure of integral bus[J]. Automotive Engineering, 2008, 30(2): 170-173. [本文引用:1] [CJCR: 0.618]
[2]	石琴, 张代胜, 谷叶水, 等. 大客车车身骨架结构强度分析及其改进设计[J]. 汽车工程, 2007, 29(1): 87-92. Shi Qin, Zhang Dai-sheng, Gu Ye-shui, et al. A study on the improvement of the strength of bus body[J]. Automotive Engineering, 2007, 29(1): 87-92. [本文引用:1] [CJCR: 0.618]
[3]	Su Rui-yi, Gui Liang-jin, Fan Zi-jie. Multi-objective optimization for bus body with strength and rollover safety constraints based on surrogate models[J]. Struct Multidisc Optim, 2011, 44(3): 431-441. [本文引用:1]
[4]	Gauchia A, Diaz V, Boada M J. Torsional stiffness and weight optimization of a real bus structure[J]. International Journal of Automotive Technology, 2010, 11(1): 41-47. [本文引用:1] [JCR: 0.69]
[5]	张军, 林程, 张国明. 基于遗传算法的客车车身骨架优化设计[J]. 北京理工大学学报, 2008, 28(1): 45-49. Zhang Jun, Lin Cheng, Zhang Guo-ming. An optimizing design method of bus body frame based on genetic algorithm[J]. Transactions of Beijing Institute of Technology, 2008, 28(1): 45-49. [本文引用:1] [CJCR: 0.529]
[6]	曹文钢, 曲令晋, 白迎春. 基于灵敏度分析的客车车身质量优化研究[J]. 汽车工程, 2009, 31(3): 278-281. Cao Wen-gang, Qu Ling-jin, Bai Ying-chun. A study on the mass optimization of bus body based on sensitivity analysis[J]. Automotive Engineering, 2009, 31(3): 278-281. [本文引用:1] [CJCR: 0.618]
[7]	张代胜, 张林涛, 谭继锦, 等. 基于刚度灵敏度分析的客车车身轻量化研究[J]. 汽车工程, 2008, 30(8): 718-720. Zhang Dai-sheng, Zhang Lin-tao, Tan Ji-jin, et al. A research on the lightweighting of bus body based on stiffness sensitivity analysis[J]. Automotive Engineering, 2008, 30(8): 718-720. [本文引用:1] [CJCR: 0.618]
[8]	Lan F, Chen J, Lin J. Comparative analysis for bus side structures and lightweight optimization[J]. Proceedings of the Institution of Mechanical Engineers Part D-Journal of Automobile Engineering, 2004, 218(D10): 1067-1075. [本文引用:1] [JCR: 0.583]
[9]	姚成, 朱铭. 全承载式客车车身结构设计[J]. 客车技术与研究, 2008(2): 13-16. Yao Cheng, Zhu Ming. Design of monocoque bus body structure[J]. Bus Technology and Research, 2008(2): 13-16. [本文引用:1] [CJCR: 0.2915]
[10]	Kalyanmoy D, Amrit P, Sameer A, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-196. [本文引用:1] [JCR: 4.81]
[11]	Zhao Wan-zhong, Wang Chun-yan, Sun Pei-kun, et al. Primary studies on integration optimization of differential steering of electric vehicle with motorized wheels based on quality engineering[J]. Science China Technological Sciences, 2011, 54(11): 3047-3053. [本文引用:1]
[12]	Gu Xian-guang, Sun Guang-yong, Li Guang-yao, et al. A comparative study on multiobjective reliable and robust optimization for crashworthiness design of vehicle structure[J]. Structural and Multidisciplinary Optimization, 2013, 48(3): 669-684. [本文引用:1] [JCR: 1.728]
[13]	Fang Lin-cun, Qin Shi-yin, Xu Gang, et al. Simultaneous optimization for hybrid electric vehicle parameters based on multi-objective genetic algorithms[J]. Energies, 2011, 4(3): 532-544. [本文引用:1] [JCR: 1.844]

2008

0.0

0.618

. 2008, 30(2):170-173

Multi-objective optimization on the body structure of integral bus

建立了全承载式大客车车身骨架的有限元模型,对车身骨架结构进行了振动模态和静力学分析.然后对车身骨架结构进行设计参数灵敏度分析,得出车身骨架扭转刚度和一阶扭转频率对各部件设计参数的灵敏度.在此基础上,以车身骨架杆件厚度为设计变量,通过两阶段结构优化设计,在整车骨架质量增加很少的条件下,提高了整车结构的扭转刚度和一阶扭转频率值;同时,一轮悬空工况下的整车结构应力峰值明显下降,应力分布更加均匀,整车骨架结构设计更为合理.

2007

0.0

0.618

. 2007, 29(1):87-92

A study on the improvement of the strength of bus body

在Unigraphics软件中建立车身骨架的线框模型后,用自行编制的接口程序生成命令流文件将模型导入到ANSYS环境中,建立了车身骨架有限元模型.用有限元理论分析了静态工况下客车车身骨架的强度特性,探讨了承载式车身骨架不同部位的受力特性.提出了通过对骨架结构进行局部改进来提高整体结构强度的方法,提出了对原结构进行改进设计的方案,并对改进前后的客车进行了强度试验,验证了改进后结构的合理性和可靠性.

2011

0.0

Struct Multidisc Optim. 2011, 44(3):431-441

Multi-objective optimization for bus body with strength and rollover safety constraints based on surrogate models

Ruiyi Su (1) , Liangjin Gui (1) , Zijie Fan (1)

1.State Key Laboratory of Automotive Safety and Energy, Department of Automotive Engineering, Tsinghua University, Beijing, 100084, China

It is important to consider the performances of lightweight, stiffness, strength and rollover safety when designing a bus body. In this paper, the finite element (FE) analysis models including strength, stiffness and rollover crashworthiness of a bus body are first built and then validated by physical tests. Based on the FE models, the design of experiment is implemented and multiple surrogate models are created with response surface method and hybrid radial basis function according to the experimental data. After that, a multi-objective optimization problem (MOP) of the bus body is formulated in which the objective is to minimize the weight and maximize the torsional stiffness of the bus body under the constraints of strength and rollover safety. The MOP is solved by employing multi-objective evolutionary algorithms to obtain the Pareto optimal set. Finally, an optimal solution of the set is chosen as the final design and compared with the original design.

2010

0.69

0.0

. 2010, 11(1):41-47 DOI:10.1007/s12239-010-0006-4

Torsional stiffness and weight optimization of a real bus structure

1.Carlos III University Mechanical Engineering Department, Research Institute of Vehicle Safety (ISVA) Avenida de la Universidad, 30 Legan’es Madrid 28911 Spain

In this paper, the structural optimization of a real bus structure is proposed. The proposed optimization has been accomplished by means of genetic algorithms. The structural behavior of the bus structure when subjected to weight and torsion was also analyzed using the finite element method (FEM). The results demonstrate that improved weight and torsional stiffness are achieved with the optimized structure.

2008

0.0

0.529

. 2008, 28(1):45-49

An optimizing design method of bus body frame based on genetic algorithm

提出一种基于遗传算法的桁架式客车车身骨架的优化设计方法.应用有限元分析软件ANSYS建立了车身骨架有限元模型并进行计算,采用遗传算法进行优化.优化后车身总质量减轻719 kg,减重比例接近25%.结果表明,基于遗传算法的优化设计明显优于常规的数学规划方法,实现了某电动大客车车身骨架的轻量化设计.

2009

0.0

0.618

. 2009, 31(3):278-281

A study on the mass optimization of bus body based on sensitivity analysis

文中将灵敏度分析引入到客车质量优化中.首先建立了某承载式客车车身的有限元模型,确定其边界条件和载荷,并对模型进行了试验验证.接着选取车架上刚度和强度相对富裕的梁作为对象进行灵敏度分析.最后根据分析结果选取车身最大应力和位移作为状态变量,以车身总质量为目标函数,进行客车车身的质量优化.

2008

0.0

0.618

. 2008, 30(8):718-720

A research on the lightweighting of bus body based on stiffness sensitivity analysis

建立了某国产全承载式客车车身有限元模型,通过静动态电测试验验证模型的准确性,进而进行刚度灵敏度分析确定优化设计变量,运用有限元分析软件进行优化.在优化的基础上提出轻量化方案,达到保证在刚度变化最小及规定强度下使车身骨架质量减轻的目标.

2004

0.583

0.0

0.2915

. , 2008(2):13-16

Design of monocoque bus body structure

介绍客车车身结构设计的力学理论,结合金旅公司已开发的具有自主知识产权的全承载车身,详细叙述全承载式客车车身结构设计采用的方法与流程,提出全承栽式客车车身制造时要注意的问题.

... 但在实际工程中,由于承载式客车的强度性能比刚度性能更容易出现问题^[9],为了保证车身结构具有足够的强度性能,设计人员在杆件的断面设计时多根据经验采取保守设计,因此产生的结构往往强度过剩,轻量化程度有限 ...

2002

4.81

0.0

... 本文所采用的多目标算法为NSGA-II,是Kalyanmoy等^[10]于2002年提出的一种基于快速非支配排序方法的多目标遗传算法 ...

2011

0.0

. 2011, 54(11):3047-3053 DOI:10.1007/s11431-011-4565-z

Primary studies on integration optimization of differential steering of electric vehicle with motorized wheels based on quality engineering

1. Department of Automotive Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China; 2. State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100086, China

The model of the differential steering system (DSS) of electric vehicle with motorized wheels and the three-degree-of-freedom dynamic model of vehicle are built. Based on these models, the concepts and quantitative expressions of steering road feel, steering portability and steering stability are proposed. Through integrating the Monte Carlo descriptive sampling, elitist non-dominated sorting genetic algorithm (NSGA-II) and Taguchi robust design method, the system parameters are optimized with steering road feel and steering portability as optimization targets, and steering stability and steering portability as constraints. The simulation results show that the system optimized based on quality engineering can improve the steering road feel, guarantee steering stability and steering portability and thus provide a theoretical basis for the design and optimization of the electric vehicle with motorized wheels system.

2013

1.728

0.0

. 2013, 48(3):669-684 DOI:10.1007/s00158-013-0921-x

A comparative study on multiobjective reliable and robust optimization for crashworthiness design of vehicle structure

<li>1.School of Mechanical and Automotive Engineering, Hefei University of Technology, 230009, Hefei, Anhui, China</li><li>4.Chery Automobile Corporation, Wuhu, 241000, China</li><li>2.State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha, 410082, China</li><li>3.School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW, 2006, Australia</li>

Abstract

Design optimization without considering uncertainties of system variables and parameters can be problematic in real life. In order to take into account the effect of uncertainties, reliable and robust design schemes have proven effective, but limited studies have been reported to compare their difference in a multiobjective framework. This paper takes a typical vehicle structure subject to offset frontal crashing scenario as an example to compare reliable and robust designs with their deterministic counterpart. The thicknesses of some key components of vehicle frontal structures were selected as design variables, the vehicle weight and energy absorption as the objectives, deceleration and firewall intrusion as the constraints. The deterministic multiobjective optimization problem was first solved by adopting Design of Experimental (DOE), metamodels and Non-dominated Sorting Genetic Algorithm II (NSGA-II). Take into account the uncertainties, a Monte Carlo Simulation (MCS) is adopted to generate random distributions of the objective and constraint functions for each design. For the reliability-based optimization the desired reliabilities of 90 %, 95 % and 99 % are considered, respectively. For the robustness-based optimization, two different formulation strategies are adopted. The optimization showed that the reliable and robust Pareto fronts are shifted away from their deterministic counterpart due to uncertainties. The different Pareto fronts yielded from the deterministic, reliable and robust designs are compared to provide some quantitative insights into how to apply these different design schemes for resolving uncertainty problems. It is shown that, compared with the baseline design, the optimizations enhance the crashworthiness of vehicle, though more conservative solutions could have been generated from the reliable and robust optimizations.

2011

1.844

0.0