选取车尾最高点、车顶最高点、车头最前端点等作为车身关键点,用参数确定这些关键点和中间过渡点的坐标以及部分曲线的端点斜率,然后用保凸曲线构成车身的三视图。俯视图和横截面图的参数是根据机件布置、乘员舒适性等空间需求确定的固定组合。把整车的长宽高、离地间隙、车轮尺寸、轮轴距作为优化问题的约束条件。车轮的尺寸、外形以及安装方式参照MIRA标准模型。

分别选择凸头车型侧视图的12个参数和凹头车型侧视图的18个参数作为优化对象,每个参数的水平数为100。

在遗传算法的评估环节中调用FLUENT等商业软件进行数值模拟计算。来流速度设为30 m/s,流模型选用可实现的 k-ε模型。为了减少计算量和计算时间,三维算例只使用半车身的计算域。通过数值试验验证,半车身算例和对称整车身算例的风阻系数 C_D值误差均小于0.1%。

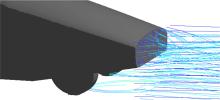
CFD计算得到的 C_D值将作为进化过程中个体适应度评估的依据,对优化方向和优化质量有着至关重要的影响,所以对CFD的计算结果进行了模型风洞试验的验证,试验模型如 图1所示。考虑到天平量程和阻塞比的问题,选用一款风阻系数较低的凸头车型带轮整车的1∶12缩比模型,在喷口面积为0.123 m²的模型风洞中进行气动试验,用六分力天平测试其气动阻力系数。连接模型和天平的支撑柱隐藏在模型的四个轮子内部,实现了试验过程中无支撑干扰。CFD结果与试验结果相比,误差小于5%,证明了本文遗传算法中使用的评估算子的可靠性。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 缩比模型的风洞试验Fig.1 Wind tunnel test for scaled model

遗传算法和车身气动优化结合的最大问题是网格生成和CFD计算的资源消耗,计算速度也是影响优化策略的重要因素。 表1列出了凸头车型三种算例的资源消耗情况。二维算例的网格生成和计算的时间和硬件需求较低,可以做几百甚至上千的大规模计算。而三维算例计算时间长、硬件需求大,只能做一百以内的小规模计算。无论是二维还是三维算例,都有一个特点:风阻系数越低,算例的收敛概率越高,收敛速度越快。可见三维算例优化更适于对风阻系数偏低的形体做中小范围调整。

表1

Table 1

表1(Table 1)

表1 不同算例的资源消耗 Table 1 Resource consumption of different cases 二维车身 三维无轮车身 带轮整车 网格数/万 20 920 920 生成时间/min 2 30 30 计算时间/h 1~4 3~10 5~15 计算资源/CPU 2 24 24

表1 不同算例的资源消耗 Table 1 Resource consumption of different cases

车身气动优化的最终目的是得到约束条件下的低风阻系数的带轮整车。因为三维算例计算量巨大,直接对带轮整车用传统遗传算法进行优化是难以实现的。二维车身能够反映三维无轮车身外流场的驻点、分离和再附着等主要流动特征。根据这个特点,可以在三维车身优化之前先利用耗时较短、硬件需求较低的二维优化阶段搜索到优化空间中的低阻区,然后再进入三维优化阶段,即在低阻区中进行局部搜索。本次优化为多参数组合优化,整个优化空间巨大。利用二维算例的灵巧性排除掉占据绝大部分的中高阻区域,为整个优化过程节约了大量时间成本。且根据前文所述低阻算例易收敛的特点,二维优化阶段可以提高后继三维优化阶段的效率。

在传统车身低阻形体求解时,车轮常被忽略。但是车轮影响车底的流场,尤其是后轮会使车底后部出现如 图2所示的回流涡,尾涡结构改变显著。而尾部流场是影响车身气动性能的最重要因素,所以在优化的过程中应该考虑车轮的影响。车轮对外流场的影响随着车轮尺寸、轮轴距的改变而改变,把车轮尺寸和位置作为约束条件之一进行优化,这种方法比在优化得到的三维无轮车身上直接添加或更换轮子的方法更符合带轮整车的气动变化规律。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 尾涡结构Fig.2 Trailing vortex structure

根据二维和三维车身算例的CFD计算特点以及气动变化规律之间的关系,确定各个阶段的优化任务及相应的优化策略。 表2为凸头车型的优化策略,凹头车型的优化策略与之基本相同。

表2

Table 2

表2(Table 2)

表2 优化策略(凸头车型) Table 2 Optimization strategy(cheese head) 阶段 二维车身 三维无轮车身 带轮整车 任务 全局搜索 局部逼近 微调 群体 60 10 10 技术 初代结合DOE 赌盘选择 赌盘选择 策略 大杂交率小 变异率 大变异率,逐渐 缩小变异步长 逐渐缩小变异 率和变异步长 代数 15 5 15 耗时 7天 5天 15天

表2 优化策略(凸头车型) Table 2 Optimization strategy(cheese head)

二维车身优化阶段的主要任务是进行全局搜索,找到邻近最优解的低阻区域。该阶段的进化初代使用了大规模的优化拉丁方分布算例(400个算例),以避免优化过程过早陷入局部优化。种群大小为60,杂交率为0.8,变异率为0.1。

三维车身和带轮整车优化阶段的主要目的是在前一阶段优化结果的基础上进行局部搜索,通过微调进一步逼近最优解。因为三维算例CFD计算的限制,后两个阶段都使用小种群进化。在这两个阶段,变异算子相当于一个环形加密算子。在带轮整车优化的最后阶段,变异率从0.8逐步缩小至0.5,变异步长从25%~40%逐步缩小至1%~10%,逐渐缩小搜索范围,直至找到最优解。

在整个优化过程中,为了防止退化,所有收敛的算例都被纳入各阶段的总库中,每一代的新群体从总库较优秀的个体中通过赌盘选择算子选择亲代进行杂交和变异。各个阶段的进化代数由实际进化情况而定。前两个阶段的优化结果不必完全收敛,一旦达到满足要求的较低 C_D值,就可以进入下一优化阶段。

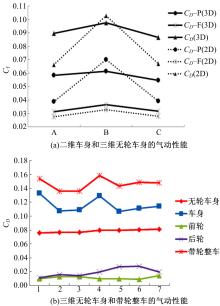
选取凸头车型的3种车身进行二维和三维无轮车身的气动性能对比试验。其中A、C车身是低尾造型,B车身为高尾造型。如 图3(a)所示,二维车身和三维车身的摩阻系数 C_f的变化趋势一致。高尾车身B和低尾车身A、C之间的二、三维的变化趋势大致相同,但低尾车身A、C之间的二、三维的变化趋势则有差异。由此可见,二维车身间的气动规律变化趋势可以反映所对应的三维车身间的气动规律的大体变化趋势,但相似车型间的变化趋势不能得到精确分辨,而这种差异会影响进化的方向和优化的质量。用二维车身进行全局搜索,探索到低阻区后转入三维车身优化阶段的方法较为合理。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同优化阶段的气动性能变化规律Fig.3 Aerodynamic performance rules for different steps

给三维无轮车身优化阶段得到的风阻系数最低的前10个车身添加轮子,淘汰不收敛算例后观查其气动规律的变化。如 图3(b)所示,带轮整车和三维无轮车身的 C_D值的变化趋势有明显的差异。7个无轮车身的 C_D值呈顺序递增趋势,而对应的带轮整车的 C_D值变化则呈无序状态。原本 C_D值最低的无轮车身在安装上轮子后 C_D值反而变成了次最大。后轮的影响比前轮的影响大,这符合前文的分析。带轮整车的 C_D约是无轮车身的1 .8 ~2 .0倍。导致 C_D增加的不仅是前后轮的风阻,最大的影响来自车身本身的风阻变化。可见车轮的增加显著改变了车身外流场的流动结构,用无轮车身不能准确预测带轮整车的 C_D变化趋势。得到低阻的三维无轮车身后继续进行带轮整车的优化,这种方法更合理并更精确。

如 图4(a)所示,凸头车型3个阶段优化结果的尾端厚度接近,头部部分轮廓线几乎重合,背部形状相似;但其中差异也较明显,例如顶点的位置,头部和后翘的形状。如 图4(b)所示,凹头车型3个阶段优化结果的尾端最高点重合,背部过渡趋势近似;带轮整车优化结果与二维车身优化结果的车头下方过渡和车头凹陷部分的形状相似。除此之外,其余部位的形状也有明显差异。这种相似性和差异性反应了分步逼近最优解的过程。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 三个阶段的优化结果侧视图Fig.4 Side views of optimization results for three steps

图5为带轮整车的优化结果,两者都为低阻车型,所以尾部流线都比较平顺,尾部侧面的拖曳涡脱落位置也比较接近。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 带轮整车优化结果图Fig.5 Oil flow diagrams of optimization results with wheels

表3为凸头车型各阶段的优化结果。如 表2和 表3所示,凸头车型二维车身优化阶段虽然进化了15代,且初代计算量较大,但只消耗了一周时间。因为有了前一阶段的铺垫,三维无轮车身优化阶段仅进化5代就得到了 C_D值低至0 .076的无轮车身。带轮整车优化阶段为了达到完全收敛状态,进化了15代使 C_D值进一步下降到0.129。 C_D值优化结果与前人通过风洞试验得到的0 .07 ~0 .09(无轮车身)、0 .14 ~0 .16(带轮整车)相比较^{[ 6]},气动性能较好。 表3中各阶段优化结果的差异进一步证实了各优化阶段气动规律的差异,也证明了分步优化的效果显著。

表3

Table 3

表3(Table 3)

表3 凸头车型各阶段的优化结果 Table 3 Optimization results of different steps(cheese head) 二维车身 优化阶段 三维无轮车身 优化阶段 带轮整车 优化阶段 二维车身 0.067 - - 三维车身 0.087 0.076 - 带轮整车 0.185 0.153 0.129

表3 凸头车型各阶段的优化结果 Table 3 Optimization results of different steps(cheese head)

整个优化过程总耗时控制在一个月内,其中带轮整车阶段花费了大半时间。如 图3(b)所示,将凸头车型三维无轮车身阶段的较优结果加上轮子后得到的带轮整车 C_D值为0 .136 ~0 .159,也处于低阻范围内。在时间和资源有限的情况下,可以选择只进行前两个阶段的优化,从而使整个优化过程缩减至两周内,可行性和实用性更高。

凹头车型带轮整车优化结果的 C_D值为0.124,其气动性能比凸头车型更好。对于凹头车型,3个阶段优化结果中头部和尾部的3个关键参数的差异小于10%。剩下的15个参数中,第2阶段和第1阶段优化结果有5个参数值差异小于10%;第3阶段优化结果有8个参数值相比第1阶段优化结果明显更靠近于第2阶段优化结果,其中有2个参数值差异小于10%。第3阶段和第1阶段优化结果没有参数值差异小于10%的参数。相隔一个阶段的第3阶段和第1阶段的继承关系较弱,说明第2阶段的过渡作用不可忽略。

凹头车型第2阶段和第1阶段优化结果的参数组合的线性相关系数为0.35,为低度线性相关关系;第3阶段和第1阶段、第2阶段的优化结果的参数组合的线性相关系数分别为0.09和0.40,前者不存在线性关系,后者为低度线性相关关系。第2阶段和第1阶段优化结果的参数组合的欧拉距离为160;第3阶段和第1阶段、第2阶段的优化结果的参数组合的线性相关系数分别为186和158,明显与前者距离大,与后者距离小。相邻两阶段优化结果的线性关系比相隔两阶段优化结果的线性关系明显,欧拉距离明显比相隔两阶段优化结果的欧拉距离小,进一步说明相邻两代具有逐步继承关系及中间阶段过渡作用的不可或缺。