基于模拟半车的悬挂自振特性试验

引用本文

王秀刚, 苏建, 曹晓宁, 林慧英, 张益瑞, 杨小敏. 基于模拟半车的悬挂自振特性试验. 44(6): 1583-1590
WANG Xiu-gang, SU Jian, CAO Xiao-ning, LIN Hui-ying, ZHANG Yi-rui, YANG Xiao-min. Experiment on natural vibration characteristics of suspension based on simulation of semi-vehicle. Journal of Jilin University Engineering and Technology Edition, 44(6): 1583-1590 复制到剪切板

Permissions

基于模拟半车的悬挂自振特性试验

王秀刚¹, 苏建¹, 曹晓宁², 林慧英¹, 张益瑞¹, 杨小敏¹

1.吉林大学交通学院,长春 130022

2.德尔福(上海)动力推进系统有限公司,上海 200131

通信作者:苏建(1954-),男,教授,博士生导师.研究方向:车辆智能检测与轨道车辆.E-mail:sujianjd@163.com

作者简介:王秀刚(1986-),男,博士研究生.研究方向:车辆智能检测与轨道车辆.

基金:吉林大学研究生创新基金项目(20121076,20121091); 中央高校基本科研业务费专项资金项目(450060487415);

摘要

建立了车体-构架双质量系统的垂向及横向振动测试模型。以齐次旋转矩阵理论为基础搭建了激振平台位姿反解模型,并对各激振器控制指令进行计算。对某型转向架悬挂实现垂向振型自振频率测试,试验结果与理论值一致,验证了本文方法的准确性。

关键词: 车辆工程; 转向架; 模拟半车; 自振频率; 位姿反解

中图分类号:U260.331 文献标志码:A 文章编号:1671-5497(2014)06-1583-08

Experiment on natural vibration characteristics of suspension based on simulation of semi-vehicle

WANG Xiu-gang¹, SU Jian¹, CAO Xiao-ning², LIN Hui-ying¹, ZHANG Yi-rui¹, YANG Xiao-min¹

1.College of Transportation, Jilin University, Changchun 130022,China

2.Delphi Shanghai Dynamics and Propulsion Systems Co., Ltd., Shanghai 200131,China

Abstract

In this paper the vertical and lateral test models of vehicle body-frame double mass system were established. The inverse displacement analysis model of the excitation platform was put forward, which was based on the theory of homogeneous rotation matrix. The control command for the vibration exciter was solved via the inverse displacement analysis model. Meanwhile, a vehicle test for vertical natural frequency was conducted. The test result was consistent with theoretical value, which proved the accuracy of the test method.

Keyword: vehicle engineering; bogie; simulation of semi-vehicle; natural frequency; inverse displacement analysis

Show Figures

轨道车辆是多自由度复杂系统,车辆行驶过程中各种激扰的耦合作用使其产生复杂的振动。准确地确定车辆振动时各振型的自振频率,避免其固有频率与外界激励频率重合,是提高车辆运行平稳性以及整车动力学性能的关键^{[ 1]}。目前悬挂自振特性的测试方法主要集中于理论计算以及室内台架试验两种方法,理论计算需对被试车辆进行简化,其结果与真实值有差异,可作为参考;室内台架试验方面,青岛四方车辆研究所及西南交通大学开发的机车车辆滚振台^{[ 2]},通过试验台的垂向、横向激振器可实现整车落成状态下的悬挂自振特性的测定,但不能够实现独立转向架自振特性的测定,具有一定的局限性。针对此类情况,吉林大学汽车运输工程研究所研发了一套可实现转向架动静态参数、车端关系以及悬挂自振特性测试的综合性试验台^{[ 3]},满足了整车落成状态以及独立转向架状态悬挂自振频率特性参数测试的需要。

本文提出了一种基于半车质量模拟的悬挂自振特性的测定方法,阐述了试验台的结构以及测试原理。建立了双质量-多自由系统的垂向及横向自振特性测试模型。搭建了基于旋转矩阵的激振台位姿反解模型,并以此为基础对各激振器控制指令进行解算。针对某型转向架实现对车体及构架垂向振型自振频率的测试,试验结果与理论值相差较小,验证了本文试验方法的准确性,为转向架设计以及悬挂参数的匹配优化提供了技术支持。

1 试验设备及方法

1.1 试验设备

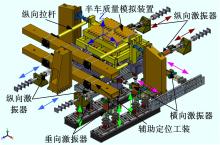
图1为转向架悬挂自振频率试验台模型,测试设备主要由半车质量模拟装置(模拟半车)、三轴向激振系统、四套纵向约束拉杆以及辅助定位工装组成。其中,半车质量模拟装置模拟车辆整备状态下转向架载荷,并由试验台下部双六自由度激振平台施加激励信号,通过三轴向激振系统(横向、纵向及垂向激振器)完成转向架在沉浮、横移、摇头、侧滚等的空间姿态模拟,实现相应振型的测定。四套纵向约束拉杆通过球铰将半车质量模拟装置与纵向支撑横梁连接在一起,四连杆机构约束了模拟车体的三个自由度,确保其能够沿 Z轴沉浮、沿 Y轴横摆和绕 X轴侧滚转动,为模拟车辆真实运行状态提供了条件。

	Figure Option View Download New Window
	图1 自振频率试验台模型Fig.1 Model of test bench for the natural frequency

1.2 试验方法

轨道车辆转向架为多自由度振动的复杂刚体,其振动环境复杂、随机性强,故采用正弦扫频试验模拟车辆的复杂振动。正弦扫频试验分为定频扫频试验及线性变频扫频试验,考虑到线性变频试验可获得较细的频率刻度,扫描精度高,试验台三轴向激振系统选用线性变频正弦激励,以一定的频率间隔从低频线性变化到高频对被试转向架进行扫频振动试验。

试验过程中,激振系统对转向架对进行正弦激振,所选择的激振频带需包含振动系统中与簧载质量及非簧载质量振动相关的主频率。同时,依据标准TB/T3115-2005(《机车车辆动力学性能台架试验方法》)有关悬挂自振特性试验的要求,设定试验扫频速度,采用激光位移传感器测定构架、车体的位移响应,并记录连续变化的响应曲线,根据车体或构架的最大振动响应点的振动频率,确定构架和车体相应振型下的自振频率。

假定激振扫频起始时刻为 t₀,相应的低频频率值为 f₀,扫频终止时刻 t对应的高频为 f₁,则频率线性变化的数学描述为:

$\begin{matrix} f = k (t - t_{0}) + f_{0} (1) \end{matrix}$

式中: k为试验扫频的速度。

根据技术协议要求,本文线性扫频激振由0时刻开始,起始频率为0.1 Hz,终止频率为10 Hz,扫频速度设定为0.035 Hz/s,频率线性变化表达式为:

$\begin{matrix} f = 0.035 t + 0.1 (2) \end{matrix}$

2 悬挂系统振动测试模型

为便于叙述,将测试模型中所涉及的参数进行汇总,如表1所示。

表1 测试模型中的相关参数 Table 1 Relevant parameters

2.1 垂向振动测试模型

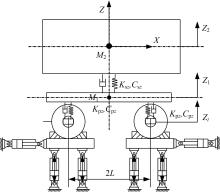
试验时,轮对与下部双六自由度平台固连,约束成一刚体,通过垂向激振器对转向架进行激励。针对本文模拟半车的测试方案,四连杆约束机构的作用,使得垂向激振时模拟半车及转向架构架垂向方向仅存在沉浮运动,同时耦合产生构架绕 Y轴的点头运动,但因垂向激振引发的构架点头角很小(最大为0.024°),故忽略该耦合运动,建立模拟半车、构架沉浮运动的2自由度垂向振动模型。系统的簧下质量只考虑其垂直方向的振动。图2为悬挂垂向振动测试模型。

	Figure Option View Download New Window
	图2 垂向振动测试模型Fig.2 Test model of vertical vibration

激振系统采用稳态正弦激励的方式,下部激振平台施加幅值为 A、频率为 ω的正弦扫频激励,即系统激励信号为: Z_t=Asin( ωt)。依据牛顿第二定律,建立系统强迫振动微分方程,以模拟车体、转向架构架沉浮运动:

$\begin{matrix} \{\begin{matrix} M_{2} {\overset{\cdot \cdot}{Z}}_{2} + 2 K_{sz} (Z_{2} - Z_{1}) + 2 C_{sz} ({\overset{\cdot}{Z}}_{2} - \overset{\cdot}{Z_{1}}) = 0; \\ M_{1} {\overset{\cdot \cdot}{Z}}_{1} - 2 K_{sz} (Z_{2} - Z_{1}) - 2 C_{sz} ({\overset{\cdot}{Z}}_{2} - {\overset{\cdot}{Z}}_{1}) + \\ 4 K_{pz} (Z_{1} - Z_{t}) + 4 C_{pz} ({\overset{\cdot}{Z}}_{1} - {\overset{\cdot}{Z}}_{t}) = 0 \end{matrix} (3) \end{matrix}$

垂向激振过程中,车体及构架的沉浮运动是耦合的,为了便于描述,引入以下参量:

m₁ = $\begin{matrix} \frac{2 K_{sz}}{M_{2}} \end{matrix}$ , m₂ = $\begin{matrix} \frac{2 C_{sz}}{M_{2}} \end{matrix}$ , m₃ = $\begin{matrix} \frac{2 K_{sz}}{M_{1}} \end{matrix}$ , m₄ = $\begin{matrix} \frac{2 C_{sz}}{M_{1}} \end{matrix}$ ,

m₅ = $\begin{matrix} \frac{(2 K_{sz} + 4 K_{pz})}{M_{1}} \end{matrix}$ , m₆ = $\begin{matrix} \frac{(2 C_{sz} + 4 C_{pz})}{M_{1}} \end{matrix}$ ,

m₇ = $\begin{matrix} \frac{4 K_{pz}}{M_{1}} \end{matrix}$ , m₈ = $\begin{matrix} \frac{4 C_{pz}}{M_{1}} \end{matrix}$ , M=A $\begin{matrix} \sqrt[]{m_{7}^{2} + w^{2} m_{8}^{2}} \end{matrix}$ ,

φ=arctan( ω $\begin{matrix} \frac{m_{8}}{m_{7}} \end{matrix}$ )

方程组(3)整理得:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot \cdot}{Z}}_{2} + m_{2} {\overset{\cdot}{Z}}_{2} - m_{2} {\overset{\cdot}{Z}}_{1} + m_{1} Z_{2} - m_{1} Z_{1} = 0; \\ {\overset{\cdot \cdot}{Z}}_{1} - m_{4} {\overset{\cdot}{Z}}_{2} + m_{6} {\overset{\cdot}{Z}}_{1} - m_{3} Z_{2} + m_{5} Z_{1} = \\ Msin (ωt + φ) 。 \end{matrix} (4) \end{matrix}$

系统的稳态强迫振动,即为方程组(4)的特解方程,设其特解为: Z₁ =λ₁sin( ωt+φ) +λ₂cos( ωt+φ); Z₂ =λ₃sin( ωt+φ) +λ₄cos( ωt+φ)。代入到式(4)得:

$\begin{matrix} \{\begin{matrix} [- m_{1} λ_{1} + m_{2} ω λ_{2} + (m_{1} - ω^{2}) λ_{3} - \\ m_{2} ω λ_{4}] \sin (ωt + φ) + \\ [- m_{2} ω λ_{1} - m_{1} λ_{2} + m_{2} ω λ_{3} + \\ (m_{1} - ω^{2}) λ_{4}] \cos (ωt + φ) = 0; \\ [(- ω^{2} + m_{5}) λ_{1} - m_{6} ω λ_{2} - \\ m_{3} λ_{3} + m_{4} ω λ_{4}] \sin (ωt + φ) + \\ [m_{6} ω λ_{1} + (- ω^{2} + m_{5}) λ_{2} - m_{4} ω λ_{3} + \\ m_{3} λ_{4}] \cos (ωt + φ) = Msin (ωt + φ) 。 \end{matrix} (5) \end{matrix}$

式(5)中按sin( ωt+φ)和cos( ωt+φ)归类消项后,得到求解系数 λ₁、 λ₂、 λ₃、 λ₄的方程组,即:

$\begin{matrix} \{\begin{matrix} - m_{1} λ_{1} + m_{2} ω λ_{2} + (m_{1} - ω^{2}) λ_{3} - m_{2} ω λ_{4} = 0; \\ - m_{2} ωλ - m_{1} λ_{2} + m_{2} ω λ_{3} + (m_{1} - ω^{2}) λ_{4} = 0; \\ (- ω^{2} + m_{5}) λ_{1} - m_{6} ω λ_{2} - m_{3} λ_{3} + m_{4} ω λ_{4} = M; \\ m_{6} ω λ_{1} + (- ω^{2} + m_{5}) λ_{2} - m_{4} ω λ_{3} + m_{3} λ_{4} = 0 。 \end{matrix} (6) \end{matrix}$

根据克莱姆线性方程组求解定理,求得各系数的值为:

$\begin{matrix} \begin{matrix} λ_{1} = \frac{|\begin{matrix} 0 & m_{2} ω & m_{1} - ω^{2} & - m_{2} ω \\ 0 & - m_{1} & m_{2} ω & m_{1} - ω^{2} \\ M & - m_{6} ω & - m_{3} & m_{4} ω \\ 0 & - ω^{2} + m_{5} & - m_{4} ω & m_{3} \end{matrix}|}{Γ} (7) \\ λ_{2} = \frac{|\begin{matrix} - m_{1} & 0 & m_{1} - ω^{2} & - m_{2} ω \\ - m_{2} ω & 0 & m_{2} ω λ_{3} & m_{1} - ω^{2} \\ - ω^{2} + m_{5} & 0 & - m_{3} & m_{4} ω \\ m_{6} ω & M & - m_{4} ω & m_{3} \end{matrix}|}{Γ} (8) \\ λ_{3} = \frac{|\begin{matrix} - m_{1} & m_{2} ω_{2} & 0 & - m_{2} ω \\ - m_{2} ω & - m_{1} & 0 & m_{1} - ω^{2} \\ - ω^{2} + m_{5} & - m_{6} ω & M & m_{4} ω \\ m_{6} ω & - ω^{2} + m_{5} & 0 & m_{3} \end{matrix}|}{Γ} (9) \\ λ_{4} = \frac{|\begin{matrix} - m_{1} & m_{2} ω_{2} & m_{1} - ω^{2} & 0 \\ - m_{2} ω & - m_{1} & m_{2} ω & 0 \\ - ω^{2} + m_{5} & - m_{6} ω & - m_{3} & M \\ m_{6} ω & - ω^{2} + m_{5} & - m_{4} ω & 0 \end{matrix}|}{Γ} (10) \\ Γ = |\begin{matrix} - m_{1} & m_{2} ω_{2} & m_{1} - ω^{2} & - m_{2} ω \\ - m_{2} ω & - m_{1} & m_{2} ω & m_{1} - ω^{2} \\ - ω^{2} + m_{5} & - m_{6} ω & - m_{3} & m_{4} ω \\ m_{6} ω & - ω^{2} + m_{5} & - m_{4} ω & m_{3} \end{matrix}| \end{matrix} \end{matrix}$

故强迫系统强迫振动时,车体及构架振动规律为:

Z₁ =λ₁sin( ωt+φ) +λ₂cos( ωt+φ) =

$\begin{matrix} \sqrt[]{{λ_{1}}^{2} + {λ_{2}}^{2}} \end{matrix}$ sin( ωt+φ+τ₁);

Z₂ =λ₃sin( ωt+φ) +λ₄cos( ωt+φ) =

$\begin{matrix} \sqrt[]{{λ_{3}}^{2} + {λ_{4}}^{2}} \end{matrix}$ sin( ωt+φ+τ₂)。

式中: τ₁为构架强迫浮沉振动与耦合激振波形的相位差, τ₁ =arctan( λ₂ /λ₁); τ₂为车体强迫浮沉振动与耦合激振波形的相位差, τ₂ =arctan( λ₄ /λ₃)。

结合车体及构架的运动规律,测试过程中运用位移传感器分别测定构架垂向的四个端头及模拟车体横向中心面下部点的垂向位移响应,并基于系统共振特性原理,测得模拟半车及构架垂向位移最大位移量时的频率值即为相应振型的自振频率。

2.2 横向振动测试模型

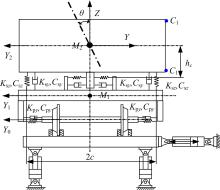
试验时,轮对与下部双六自由度平台固连成一整体,通过横向激振器对轮对进行激励。考虑到模拟半车测试方案中四连杆机构纵向方向的约束作用,使模拟车体在横向激励过程中具有横摆、侧滚2个自由度,构架在横向激励过程中具有横摆、侧滚及摇头3个自由度。但横向激励耦合产生的构架摇头角及侧滚角很小,故可忽略构架摇头、侧滚的自由度,即建立模拟半车横摆、侧滚运动及构架横摆运动的3自由度横向振动模型。图3为悬挂横向振动测试模型。

	Figure Option View Download New Window
	图3 横向振动测试模型Fig.3 Test model of lateral vibration

试验台横向激振器对转向架施加幅值为 D、频率为 ω的正弦扫频激励,即系统激励信号为: Y₀ =Dsin( ωt)。根据牛顿第二定律,建立系统强迫振动微分方程,以模拟车体横摆、侧滚运动以及构架横摆运动:

$\begin{matrix} \{\begin{matrix} M_{2} {\overset{\cdot \cdot}{Y}}_{2} + 2 K_{ssy} (Y_{2} - Y_{1} + h_{c} θ) + \\ 2 C_{sy} ({\overset{\cdot}{Y}}_{2} - {\overset{\cdot}{Y}}_{1} + h_{c} \overset{\cdot}{θ}) = 0 \\ J_{c} \overset{\cdot \cdot}{θ} - 2 K_{sz} c^{2} θ - 2 C_{sz} c^{2} \overset{\cdot}{θ} - 2 K_{sy} h_{c} (Y_{2} - Y_{1} + h_{c} θ) - \\ 2 C_{sy} h_{c} ({\overset{\cdot}{Y}}_{2} - {\overset{\cdot}{Y}}_{1} + h_{c} \overset{\cdot}{θ}) - m_{2} g h_{c} θ = 0 \\ M_{1} {\overset{\cdot \cdot}{Y}}_{1} - 2 K_{sy} (Y_{2} - Y_{1} + h_{c} θ) - 2 C_{sy} ({\overset{\cdot}{Y}}_{2} - {\overset{\cdot}{Y}}_{1} + \\ h_{c} \overset{\cdot}{θ}) - 4 K_{py} (Y_{1} - Y_{0}) + 4 C_{pz} ({\overset{\cdot}{Y}}_{1} - {\overset{\cdot}{Y}}_{0}) = 0 \end{matrix} (11) \end{matrix}$

横向激振过程中,车体横摆、侧滚运动以及构架横摆运动是耦合的,为便于描述,引入以下参量:

k₁ = $\begin{matrix} \frac{2 c^{2} C_{sz} + 2 {h_{c}}^{2} C_{sy}}{J_{c}} \end{matrix}$ ,

k₂ = $\begin{matrix} \frac{2 c^{2} K_{sz} + 2 {h_{c}}^{2} K_{sy} + M_{2} g h_{c}}{J_{c}} \end{matrix}$ ,

k₃ = $\begin{matrix} \frac{2 h_{c} K_{sy}}{J_{c}} \end{matrix}$ , k₄ = $\begin{matrix} \frac{2 h_{c} C_{sy}}{J_{c}} \end{matrix}$ ; a₁ = $\begin{matrix} \frac{2 C_{sy}}{M_{2}} \end{matrix}$ ,

a₂ = $\begin{matrix} \frac{2 K_{sy}}{M_{2}} \end{matrix}$ ; b₁ = $\begin{matrix} \frac{2 C_{sy}}{M_{1}} \end{matrix}$ , b₂ = $\begin{matrix} \frac{2 K_{sy}}{M_{1}} \end{matrix}$ ,

b₃ = $\begin{matrix} \frac{2 K_{sy} - 4 K_{py}}{M_{1}} \end{matrix}$ , b₄ = $\begin{matrix} \frac{2 C_{sy} + 4 C_{py}}{M_{1}} \end{matrix}$ 。

则方程组(11)整理得:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot \cdot}{Y}}_{2} + a_{1} h_{c} \overset{\cdot}{θ} + a_{2} h_{c} θ + a_{2} Y_{2} + a_{1} {\overset{\cdot}{Y}}_{2} - a_{2} Y_{1} - a_{1} \overset{\cdot}{Y_{1}} = 0; \\ \overset{\cdot \cdot}{θ} - K_{1} \overset{\cdot}{θ} - K_{2} θ - K_{3} Y_{2} - K_{4} {\overset{\cdot}{Y}}_{2} + K_{3} Y_{1} + K_{4} {\overset{\cdot}{Y}}_{1} = 0; \\ {\overset{\cdot \cdot}{Y}}_{1} - b_{1} h_{c} \overset{\cdot}{θ} - b_{2} h_{c} θ - b_{2} Y_{2} - b_{1} {\overset{\cdot}{Y}}_{2} + b_{3} Y_{1} + b_{4} {\overset{\cdot}{Y}}_{1} = \\ (b_{4} - b_{1}) {\overset{\cdot}{Y}}_{0} + (b_{3} - b_{2}) Y_{0} 。 \end{matrix} (12) \end{matrix}$

设方程组(12)非齐次微分方程的解为:

$\begin{matrix} \{\begin{matrix} Y_{1} = B_{1} \sin (ωt + φ) + B_{2} \cos (ωt + φ); \\ Y_{2} = C_{1} \sin (ωt + φ) + C_{2} \cos (ωt + φ); \\ θ = A_{1} \sin (ωt + φ) + A_{2} \cos (ωt + φ) 。 \end{matrix} \end{matrix}$

代入到式(12),归类、消项整理得:

$\begin{matrix} \{\begin{matrix} [a_{2} h_{c} A_{1} - a_{1} h_{c} ω A_{2} - a_{2} B_{1} + a_{1} ω B_{2} + \\ (a_{2} - ω^{2}) C_{1} - a_{1} ω C_{2}] \sin (ωt + φ) + \\ [a_{1} h_{c} A_{1} + a_{2} h_{c} A_{2} - a_{1} ω B_{1} - a_{2} B_{2} + \\ a_{1} ω C_{1} + (a_{2} - ω^{2}) C_{2}] \cos (ωt + φ) = 0; \\ [(- ω^{2} - k_{2}) A_{1} + k_{1} ω A_{2} + k_{3} B_{1} - k_{4} ω B_{2} - \\ k_{3} C_{1} + k_{4} ω C_{2}] \sin (ωt + φ) + [- k_{1} A_{1} + \\ (- ω^{2} - k_{2}) A_{2} + k_{4} ω B_{1} + k_{3} B_{2} - \\ k_{4} ω C_{1} - k_{3} C_{2}] \cos (ωt + φ) = 0; \\ [- b_{2} h_{c} A_{1} + b_{1} h_{c} ω A_{2} + (b_{3} - ω^{2}) B_{1} - \\ b_{4} ω B_{2} - b_{2} C_{1} + b_{1} ω C_{2}] \sin (ωt + φ) + \\ [- b_{1} h_{c} ω A_{1} - b_{2} h_{c} A_{2} + b_{4} ω B_{1} + (b_{3} - \\ ω^{2}) B_{2} - b_{4} ω C_{1} - b_{3} C_{2}] \cos (ωt + φ) = \\ (b_{3} - b_{2}) Dsin (ωt + φ) + \\ (b_{4} - b_{1}) Dωcos (ωt + φ) 。 \end{matrix} \end{matrix}$ (13)

由方程组(13)得到求解待定系数 A₁、 A₂、 B₁、 B₂、 C₁、 C₂的6个联立方程,即:

$\begin{matrix} \{\begin{matrix} a_{2} h_{c} A_{1} - a_{1} h_{c} ω A_{2} - a_{2} B_{1} + a_{1} ω B_{2} + \\ (a_{2} - ω^{2}) C_{1} - a_{1} ω C_{2} = 0; \\ a_{1} h_{c} A_{1} + a_{2} h_{c} A_{2} - a_{1} ω B_{1} - a_{2} B_{2} + \\ a_{1} ω C_{1} + (a_{2} - ω^{2}) C_{2} = 0; \\ (- ω^{2} - k_{2}) A_{1} + k_{1} ω A_{2} + k_{3} B_{1} - \\ k_{4} ω B_{2} - k_{3} C_{1} + k_{4} ω C_{2} = 0; \\ - k_{1} A_{1} + (- ω^{2} - k_{2}) A_{2} + k_{4} ω B_{1} + \\ k_{3} B_{2} - k_{4} ω C_{1} - k_{3} C_{2} = 0; \\ - b_{2} h_{c} A_{1} + b_{1} h_{c} ω A_{2} + (b_{3} - ω^{2}) B_{1} - \\ b_{4} ω B_{2} - b_{2} C_{1} + b_{1} ω C_{2} = D (b_{3} - b_{2}) - \\ b_{1} h_{c} ω A_{1} - b_{2} h_{c} A_{2} + b_{4} ω B_{1} + (b_{3} - \\ ω^{2}) B_{2} - b_{4} ω C_{1} - b_{3} C_{2} = Dω (b_{4} - b_{1}) 。 \end{matrix} (14) \end{matrix}$

根据克莱姆线性方程组求解定理,解方程组(14)可求得各系数的值,即:

A₁ =

$\begin{matrix} \frac{|\begin{matrix} 0 & - a_{1} h_{c} ω & - a_{2} & a_{1} ω & a_{2} - ω^{2} & - a_{1} ω \\ 0 & a_{2} h_{c} & - a_{1} ω & - a_{2} & a_{1} ω & a_{2} - ω^{2} \\ 0 & k_{1} ω & k_{3} & - k_{4} ω & - k_{3} & k_{4} ω \\ 0 & - ω^{2} & - k_{2} & k_{4} ω & k_{3} & - k_{4} ω & - k_{3} \\ D (b_{3} - b_{2}) & b_{1} h_{c} ω & b_{3} - ω^{2} & - b_{4} ω & - b_{2} & b_{1} ω \\ Dω (b_{4} - b_{1}) & - b_{2} h_{c} & b_{4} ω & b_{3} - ω^{2} & - b_{4} ω & - b_{3} \end{matrix}|}{Λ} \end{matrix}$

A₂ =

$\begin{matrix} \frac{|\begin{matrix} a_{2} h_{c} & 0 & - a_{2} & a_{1} ω & a_{2} - ω^{2} & - a_{1} ω \\ a_{1} h_{c} & 0 & - a_{1} ω & - a_{2} & a_{1} ω & a_{2} - ω^{2} \\ - ω^{2} - k_{2} & 0 & k_{3} & - k_{4} ω & - k_{3} & k_{4} ω \\ - k_{1} & 0 & - k_{2} & k_{4} ω & k_{3} & - k_{4} ω & - k_{3} \\ - b_{2} h_{c} & D (b_{3} - b_{2}) & b_{3} - ω^{2} & - b_{4} ω & - b_{2} & b_{1} ω \\ - b_{1} h_{c} ω & Dω (b_{4} - b_{1}) & b_{4} ω & b_{3} - ω^{2} & - b_{4} ω & - b_{3} \end{matrix}|}{Λ} \end{matrix}$

Λ=

$\begin{matrix} |\begin{matrix} a_{2} h_{c} & - a_{1} h_{c} ω & - a_{2} & a_{1} ω & a_{2} - ω^{2} & - a_{1} ω \\ a_{1} h_{c} & a_{2} h_{c} & - a_{1} ω & - a_{2} & a_{1} ω & a_{2} - ω^{2} \\ - ω^{2} - k_{2} & k_{1} ω & k_{3} & - k_{4} ω & - k_{3} & k_{4} ω \\ - k_{1} & - ω^{2} & - k_{2} & k_{4} ω & k_{3} & - k_{4} ω & - k_{3} \\ - b_{2} h_{c} & b_{1} h_{c} ω & b_{3} - ω^{2} & - b_{4} ω & - b_{2} & b_{1} ω \\ - b_{1} h_{c} ω & - b_{2} h_{c} & b_{4} ω & b_{3} - ω^{2} & - b_{4} ω & - b_{3} \end{matrix}| \end{matrix}$

同理,可求得 B₁、 B₂、 C₁、 C₂的解,由此便可求得横向强迫振动时车体横摆、侧滚运动及构架横摆运动的振动规律,即:

$\begin{matrix} \{\begin{matrix} Y_{1} = B_{1} \sin (ωt + φ) + B_{2} \sin (ωt + φ) = \\ \sqrt[]{{B_{1}}^{2} + {B_{2}}^{2}} \sin (ωt + φ + δ_{1}); \\ Y_{2} = C_{1} \sin (ωt + φ) + C_{2} \sin (ωt + φ) = \\ \sqrt[]{{C_{1}}^{2} + {C_{2}}^{2}} \sin (ωt + φ + δ_{2}); \\ θ = A_{1} \sin (ωt + φ) + A_{2} \sin (ωt + φ) = \\ \sqrt[]{{A_{1}}^{2} + {A_{2}}^{2}} \sin (ωt + φ + δ_{3}) 。 \end{matrix} \end{matrix}$

式中: δ₁为构架横摆强迫振动与耦合激振波形的相位差, δ₁ =arctan( B₂ /B₁); δ₂为车体横摆强迫振动与耦合激振波形的相位差, δ₂ =arctan( C₂ /C₁); δ₃为车体横摆强迫振动与耦合激振波形的相位差, δ₃ =arctan( A₂ /A₁)。

由于车辆本身结构及一二系悬挂弹性约束的作用,车体横摆及侧滚运动是耦合叠加的,并表现为车体下心滚摆和上心滚摆^{[ 4]}。试验过程中,结合车体横摆、侧滚的振动规律,运用激光位移传感器实时测定模拟车体侧墙上部点( C₁)及下部点( C₂)的横向位移量,依据上、下部点横向位移的相位关系判定车体振型。

当车体以某一低频 ω₁作耦合的横摆及侧滚振动时,二者是同相位的,两种耦合振动的绕点在车体重心以下,亦即下心滚摆;当车体以某一高频 ω₂作耦合的横摆及侧滚振动时,二者是反相位的,两种耦合振动的绕点在车体重心以上,亦即上心滚摆。同时,对模拟车体侧墙上下部点的时域信号做FFT变换求得车体相应振型下的自振频率。

3 试验测点布局

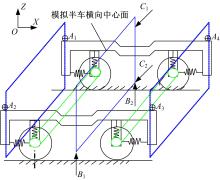
依据本文模拟半车的测试方案,测点的布局需反映车体及构架的主要振型。试验过程中,运用试验台三轴向激振系统对轮对进行激励,对被试转向架施加正弦变频加载。同时,结合模拟半车的结构特点,选用多点测量方式,以能反映车体及构架的振动特性及相互的关系。试验各测试点的布局如图4所示。

	Figure Option View Download New Window
	图4 测点布局示意图Fig.4 Schematic diagram of measuring point position

将位移传感器布置在车体横向中心面(实线框),即模拟半车垂向自振特性测点为 B₁、 B₂,测定模拟车体两下部点垂向位移响应;横向振动测点为 C₁、 C₂,测定模拟车体上下部点的横向位移响应。测定构架垂向自振特性时,将转向架划分为2个截面(虚线框),每个截面布置2个测点(见图4中 A₁、 A₂、 A₃、 A₄),即测点布置在构架垂向四个端头。

4 位姿反解

上述测试的实现需在建立试验台位姿反解基础上,将解算指令输入到各向激振器,实现相应振型的测试。结合试验台结构,将其简化为如图5所示的形式。建立全局坐标系(地面静坐标系) O-XYZ,取列车行驶方向为 X轴、平行于轮轴的方向为 Y轴、垂直轨面的方向为 Z轴;建立两下六自由度平台的局部坐标系(体坐标系) O₁ -x₁ y₁ z₁及 O₂ -x₂ y₂ z₂,选取下平台横向作动器横向中心线与两纵向作动器横向间距中线的交点为局部坐标系坐标原点 O₁、 O₂。

体坐标相对于静坐标的位姿表述采用广义坐标 q=( q₁, q₂, q₃, q₄, q₅, q₆)描述, q_i( i=1,2,3)为体坐标系相对于静坐标系的3个绕 x, y, z轴的旋转量; q_i( i=4,5,6)为体坐标原点相对于静坐标系沿 x, y, z三个坐标轴的平移量^[5 ^-^6]。图5中1 ~14为作动器下铰链点;1 '~14 '为作动器上铰链点; l₁ ~l₄、 v₁ ~v₂、 h₁ ~h₄为试验台几何关系参量。

	Figure Option View Download New Window
	图5 试验台简图Fig.5 Sketch of the test-bed

结合试验台几何尺寸关系,建立作动器1~7上铰链点 A₁、下铰链点 B₁在局部坐标系中的坐标向量:

$\begin{matrix} \begin{matrix} A_{1} = [\begin{matrix} l_{1} & l_{1} & - l_{1} & - l_{1} & l_{2} & l_{2} & 0 \\ - h_{1} & h_{1} & h_{1} & - h_{1} & - h_{2} & h_{2} & h_{3} \\ - v_{1} & - v_{1} & - v_{1} & - v_{1} & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{matrix}] \\ B_{1} = [\begin{matrix} l_{1} & l_{1} & - l_{1} & - l_{1} & l_{2} & l_{2} & 0 \\ - h_{1} & h_{1} & h_{1} & - h_{1} & - h_{2} & h_{2} & h_{3} \\ - v_{2} & - v_{2} & - v_{2} & - v_{2} & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{matrix}] (15) \end{matrix} \end{matrix}$

作动器8~14上铰链点 A₂、下铰链点 B₂在局部坐标系中的坐标向量:

$\begin{matrix} \begin{matrix} A_{2} = [\begin{matrix} - l_{1} & - l_{1} & l_{1} & l_{1} & - l_{2} & - l_{2} & 0 \\ - h_{1} & h_{1} & h_{1} & - h_{1} & - h_{2} & h_{2} & h_{3} \\ - v_{1} & - v_{1} & - v_{1} & - v_{1} & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{matrix}] \\ B_{2} = [\begin{matrix} - l_{1} & - l_{1} & l_{1} & l_{1} & - l_{2} & - l_{2} & 0 \\ - h_{1} & h_{1} & h_{1} & - h_{1} & - h_{2} & h_{2} & h_{3} \\ - v_{2} & - v_{2} & - v_{2} & - v_{2} & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{matrix}] (16) \end{matrix} \end{matrix}$

体坐标系相对于静坐标系进行 ZYX旋转矩阵变换,得到齐次变换矩阵 $\begin{matrix} {T_{i}}^{[7 - 8]} \end{matrix}$ ,即:

$\begin{matrix} T_{i} = [\begin{matrix} \cos q_{2} \cos q_{3} & - \cos q_{1} \sin q_{3} + \sin q_{1} \sin q_{2} \cos q_{3} & \sin q_{1} \sin q_{3} + \cos q_{1} \sin q_{2} \cos q_{3} & q_{4} \\ \cos q_{2} \sin q_{3} & \cos q_{1} \cos q_{3} + \sin q_{1} \sin q_{2} \sin q_{3} & - \sin q_{1} \cos q_{3} + \cos q_{1} \sin q_{2} \sin q_{3} & q_{5} \\ - \sin q_{2} & \sin q_{1} \cos q_{2} & \cos q_{1} \cos q_{2} & q_{6} \\ 0 & 0 & 0 & 1 \end{matrix}] (17) \end{matrix}$

综上所述,作动器伸缩量分别为:

$\begin{matrix} \begin{matrix} Δ L_{ij} = ‖ A_{i} T_{i} - B_{i} ‖- L_{ij}^{0} (18) \\ i = 1,2, 3; j = 1,2, \dots, 7 \end{matrix} \end{matrix}$

式中: $\begin{matrix} L_{ij}^{0} \end{matrix}$ 为作动器初始伸长量。

结合文中建立的位姿解算模型,运用MATLAB编程实现悬挂自振特性试验各作动器位移指令的实时计算,并将控制命令输入到下部双六自由度平台各激振器,实现各振型自振特性的测定。

5 实车试验

以某型转向架进行模拟半车质量下的悬挂自振频率测试。图6为转向架构架垂向自振频率试验测点 A₁、 A₂、 A₃、 A₄的时域及频域曲线,以及车体浮沉自振频率试验测点 B₁、 B₂的时域及频域曲线。本文仅对悬挂垂直自振特性进行分析,该型车整备状态下总质量为44 t,试验采用模拟半车质量为22.1 t,接近实车状态。试验时,试验台下

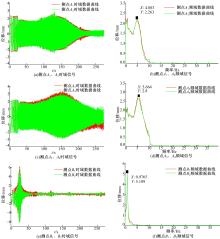	Figure Option View Download New Window
	图6 测点 A₁、 A₂、 A₃、 A₄、 B₁、 B₂的时域和频域信号Fig.6 Time domain signal and frequency domain signal of measuring point A₁, A₂, A₃, A₄, B₁ and B₂

部垂向激振器对被试转向架的轮对施加正弦线性扫频激励,激励振幅为2 mm,激励频率为0.1~10 Hz,扫频速度为0.035 Hz/s;同时,根据第3节所确定的测点布局进行激光位移传感器的布置,测定记录构架及车体在垂向方向上的位移变化,根据车体及构架的最大振动响应点的振动频率,确定其垂向振型下的自振频率。

测点 A₁、 A₂布置在靠近试验台四连杆机构一侧的构架两端头;测点 A₃、 A₄布置在另一侧的构架两端头。依据时域曲线分析可知,测点 A₁、 A₂及 A₃、 A₄的位移响应总的变化趋势基本一致,但在高频扫频阶段测点 A₁、 A₂位移响应的衰减速度快于测点 A₃、 A₄,且在共振点时的位移量较测点 A₃、 A₄小。由图6(a)(b)(c)(d)的幅频特性曲线可知,测点 A₁、 A₂处的自振频率值为4.883 Hz;测点 A₃、 A₄处的自振频率值为5.664 Hz,其理论值为6.23 Hz,其误差为9%,误差较小。同时,可判定一系悬挂弹簧阻尼等参数匹配具有差异性,对优化车辆整体设计具有指导作用。

测点 B₁、 B₂布置于模拟半车横向中心面的底端,测定车体的垂向自振频率。由图6(e)(f)可知,测点 B₁及测点 B₂位移响应的变化趋势吻合,但达到最大位移响应点后,测点 B₂的衰减速度较快;由幅频特性曲线分析,可知车体浮沉的自振频率较低,其值为0.9765 Hz,且两测点的值一致,其理论值为0.93 Hz,误差为4.9%,误差较小。同时判定二系悬挂弹簧阻尼等参数匹配较合理。另外,结合图6(a)(b)(c)(d)的时域信号曲线可知,由于车体及构架浮沉运动的耦合性,在低频扫频阶段构架同样产生了较大位移量。

综上所述,车体、构架双质量弹簧系统的浮沉运动主要表现为两种振型,在强迫振动的低频扫频阶段产生低频共振,即车身型振动;在强迫振动的高频扫频阶段产生高频共振,即构架型振动。

6 结束语

提出了基于半车质量模拟的悬挂自振特性测定方法,阐述了试验台的结构以及测试原理;建立了针对悬挂浮沉、车体上心滚摆及下心滚摆振型自振频率的测试模型。结合试验台结构,借助于齐次旋转矩阵方法搭建了激振台位姿反解模型,并以此为基础对各激振器控制指令进行计算。对模型转向架进行了悬挂垂向自振频率的测试, 结

果与理论计算相一致,误差较小,验证了测试模型及方法的可行性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王贺鹏. 车体自振频率的研究[D]. 大连: 大连交通大学交通运输工程学院, 2004. Wang He-peng. Car body self-vibration frequency study[D]. Dalian: School of Transportation Engineering, Dalian Jiaotong University, 2004. [本文引用:1] [CJCR: 0.2584]
[2]	黄丽湘, 张卫华, 马启文. 机车车辆整车滚动振动试验台设计[J]. 铁道车辆, 2007, 45(1): 5-9. Huang Li-xiang, Zhang Wei-hua, Ma Qi-wen. Design of rolling and vibration test rig for complete locomotive and rolling stock[J]. Rolling Stock, 2007, 45(1): 5-9. [本文引用:1] [CJCR: 0.1319]
[3]	吉林大学. 一种龙门框架式轨道车辆转向架参数测定试验台[P]. 中国: ZL201220476652. 9, 2013-03-27. [本文引用:1]
[4]	陈林. 基于试验模态分析的动车组动态设计研究[D]. 成都: 西南交通大学交通运输与物流学院, 2009. Chen Lin. Study on dynamic design of EMU based on experimental modal analysis[D]. School of Transportation and Logistics, Southwest Jiaotong University, 2009. [本文引用:1]
[5]	王秀刚, 苏建, 曹晓宁, 等. 转向架三轴向转动惯量测试方法[J]. 华南理工大学学报: 自然科学版, 2012, 40(11): 71-77. Wang Xiu-gang, Su Jian, Cao Xiao-ning, et al. Test method for 3-axis rotational inertia of bogie[J]. Journal of South China University of Technology (Natural Science), 2012, 40(11): 71-77. [本文引用:1] [CJCR: 0.726]
[6]	Bai S P, Hansen M R, Angeles J. A robust forward-displacement analysis of spherical parallel robots[J]. Mechanism and Machine Theory2009, 44(12): 2204-2216. [本文引用:1] [JCR: 1.214]
[7]	任敬轶. 一种三分支空间机器人的位姿反解[J]. 机械工程学报, 2001, 37(10): 64-68. Ren Jing-yi. Inverse displacement solution to a three-branch space robot system[J]. Chinese Journal of Mechanical Engineering, 2001, 37(10): 64-68. [本文引用:1] [JCR: 0.263] [CJCR: 0.6991]
[8]	张尚盈, 赵慧, 韩俊伟. 六自由度运动平台实时控制的正/反解算法[J]. 机床与液压, 2003(3): 133-135. Zhang Shang-ying, Zhao Hui, Han Jun-wei. Direct and reverse algorithms for real-time control of 6-DOF platform[J]. Machine Tool & Hydraulics, 2003(3): 133-135. [本文引用:1]

2004

0.0

0.2584

... 准确地确定车辆振动时各振型的自振频率,避免其固有频率与外界激励频率重合,是提高车辆运行平稳性以及整车动力学性能的关键^[1] ...

2007

0.0

0.1319

... 室内台架试验方面,青岛四方车辆研究所及西南交通大学开发的机车车辆滚振台^[2],通过试验台的垂向、横向激振器可实现整车落成状态下的悬挂自振特性的测定,但不能够实现独立转向架自振特性的测定,具有一定的局限性 ...

0.0

... 针对此类情况,吉林大学汽车运输工程研究所研发了一套可实现转向架动静态参数、车端关系以及悬挂自振特性测试的综合性试验台^[3],满足了整车落成状态以及独立转向架状态悬挂自振频率特性参数测试的需要 ...

2009

0.0

... 由于车辆本身结构及一二系悬挂弹性约束的作用,车体横摆及侧滚运动是耦合叠加的,并表现为车体下心滚摆和上心滚摆^[4] ...

2012

0.0

0.726

2009

1.214

0.0

. 2009, 44(12):2204-2216 DOI:10.1016/j.mechmachtheory.2009.07.005

A robust forward-displacement analysis of spherical parallel robots

Abstract

The forward-displacement analysis of spherical parallel robots (SPRs) is revisited. A robust approach, based on the input–output (I/O) equation of spherical four-bar linkages, is proposed. In this approach, the closed-loop kinematic chain of a SPR is partitioned into two four-bar spherical chains, whose I/O equations are at the core of the analysis reported here. These equations lead to a trigonometric equation in the joint angles, which is solved semigraphically to obtain the joint variables for the determination of the moving plate orientation. Examples are included to demonstrate the application of the method.

... q_i(i=4,5,6)为体坐标原点相对于静坐标系沿x,y,z三个坐标轴的平移量^[5^-^6] ...

2001

0.263

0.6991

. 2001, 37(10):64-68

Inverse displacement solution to a three-branch space robot system

具有多分支的空间机器人系统在不久的将来应会成为宇宙空间探索的有利工具.这样的系统与常见的串联或并联机器人有许多不同之处,它同时具有串联机器人和并联机器人的一些特点.为此,提出了一种具有三分支的空间机器人模型,根据该模型所具有的结构特征并结合并联机器人位姿正解方面的研究成果,给出了一种计算这种机器人位姿反解的方法.运用该算法可以方便、快捷地算出系统所有可能的位姿反解.

0.0

. , 2003(3):133-135

Direct and reverse algorithms for real-time control of 6-DOF platform

本文详细研究了六自由度运动平台的正解和反解,提出的正解算法具有算法简单、解算效率高和易于编程实现等优点,可应用于六自由度运动平台的实时控制中.本算法已经在MATLAB的Simulink中利用xPC Target技术和模块编程的思想得到实现.最后,文中通过一实例说明了该算法的高效性.