基于速度和加速度概率分布的电动汽车能耗计算模型

引用本文

隗海林, 赖祥翔, 黄朝胜, 施树明, 王海洲. 基于速度和加速度概率分布的电动汽车能耗计算模型. 44(6): 1591-1595
KUI Hai-lin, LAI Xiang-xiang, HUANG Chao-sheng, SHI Shu-ming, WANG Hai-zhou. EV calculation model of energy consumption based on velocity and acceleration distribution. Journal of Jilin University Engineering and Technology Edition, 44(6): 1591-1595 复制到剪切板

Permissions

基于速度和加速度概率分布的电动汽车能耗计算模型

隗海林¹, 赖祥翔^1,², 黄朝胜³, 施树明¹, 王海洲¹

1.吉林大学交通学院,长春 130022

2.上海汽车集团股份有限公司乘用车技术中心,上海 201804

3.中国第一汽车集团公司技术中心,长春 130011

通信作者:施树明(1965-)男,教授,博士生导师.研究方向:车辆运行仿真.E-mail:shishuming@jlu.edu.cn

作者简介:隗海林(1969)男,教授,博士生导师.研究方向:车辆节能技术.E-mail：khl69@163.com

基金:“973”国家重点基础研究发展计划项目(2010CB736101);

摘要

根据随机过程遍历性理论以及电动汽车能耗在速度时间序列上的时间平均与在VA(速度-加速度)相空间的统计平均之间的等价关系,建立了基于VA概率分布的电动汽车能耗计算模型。相比以往的利用速度时间序列计算能耗,基于VA概率分布能耗模型的计算效率得到了很大提高,能够满足电动汽车道路能耗实时计算的要求。通过道路试验能耗与基于VA概率分布能耗模型仿真计算结果的对比,表明模型具有较高的计算精度。

关键词: 车辆工程; 电动汽车能耗; 遍历性理论; 能耗计算效率

中图分类号:U471.23 文献标志码:A 文章编号:1671-5497(2014)06-1591-05

EV calculation model of energy consumption based on velocity and acceleration distribution

KUI Hai-lin¹, LAI Xiang-xiang^1,², HUANG Chao-sheng³, SHI Shu-ming¹, WANG Hai-zhou¹

1.College of Transportation, Jilin University, Changchun 130022,China

2.Passenger Car Technology Center, SAIC Motor Co., Ltd., Shanghai 201804, China

3.R&D Center, China FAW Group Corporation, Changchun 130011, China

Abstract

According to the theory of ergodic property of stochastic process and the equivalence relation between time average of the energy consumption in velocity time series and statistical average of energy consumption in Velocity-and-Acceleration (VA) phase space, a model, which can calculate EV energy consumption based on VA probability distribution, was built up. Compared to the energy consumption model based on velocity time series, the efficiency of energy consumption calculation of the new model is greatly improved, meeting the demand of real-time calculation of EV energy consumption in urban route. The calculation accuracy of the model is validated by comparative tests between EV trial on the route of Changchun city and energy consumption simulation using the proposed model.

Keyword: vehicle engineering; energy consumption of EV; theory of ergodic property; efficiency of energy consumption calculation

Show Figures

0 引言

评价电动汽车能耗水平的模型一般分为两类:一类为宏观能耗计算模型;另一类为微观能耗计算模型^{[ 1]}。它们的主要区别在于计算能耗的方法和时间尺度不同。宏观能耗计算模型主要是采用调查和统计的方法,通过采集和统计能耗数据得出一段时间内的汽车平均能耗数值,计算的时间尺度达到了月甚至年,主要的目的就是用来总体评价一段时间内汽车的平均能耗情况,具有代表性的模型为美国环保署开发的MOBILE6^{[ 2]};微观能耗计算模型主要是根据整车在具体道路上运行的特征数据进行瞬时能耗计算,时间尺度一般为秒、分或者小时。微观能耗模型主要分为两种:一种通过拟合方法建立汽车运行状态与能耗之间的关系,具有代表性的模型是美国弗吉尼亚理工大学交通系的Ahn和土木工程系的Rakha、Trani合作开发的VT micro model^{[ 3]};另一种是通过整车动力学分析建立整车瞬时运行状态与能耗的关系,具有代表性的模型是美国通用汽车研究实验室Gino和Mark的基于车辆运行工况速度时间序列的汽车能耗计算模型^{[ 4]}。

本文研究了电动汽车瞬时能耗的计算方法,为电动汽车通过实时计算能耗来选择节能路径进而提高续驶里程提供了有效依据。由于电动汽车和传统燃油汽车在动力学分析上没有本质区别^{[ 5]},以动力学分析为基础建立的电动汽车能耗模型的分析方法与传统燃油汽车差别很小,因此本文方法也适用于传统燃油汽车。

1 已有瞬时能耗计算模型的局限性

已有的基于速度时间序列汽车瞬时能耗计算模型是在整车动力学分析基础之上,根据电动汽车运行状态的速度时间序列来计算能耗的^{[ 6, 7]}。

已知汽车行驶方程式^{[ 8]}:

$\begin{matrix} F = mgf + mgi + δm \frac{dv}{dt} + \frac{ρ C_{D} A}{2} v^{2} (1) \end{matrix}$

式中: m为汽车的整备质量,kg; f为滚动阻力系数; i为道路坡度,城市道路坡度变化不大,坡度一般取为零; δ为旋转质量换算系数; ρ为空气密度,一般取 ρ=1.2258 kg/m³; C_D为空气阻力系数; A为迎风面积; v为车速,m/s。

当电动汽车处于匀速或加速行驶状态时,忽略坡度的影响,驱动力为:

$\begin{matrix} F_{t} = mgf + δm \frac{dv}{dt} + \frac{ρ C_{D} A}{2} v^{2} (2) \end{matrix}$

式中: F_t为驱动力;则驱动消耗的能量(kWh)为:

$\begin{matrix} E_{t} = \overset{t_{1}}{\sum_{t = 1}} \frac{F_{t} v}{1000} Δt / 3600 (3) \end{matrix}$

同理,当电动汽车处于减速状态时,制动力为:

$\begin{matrix} F_{b} = mgf + δm \frac{dv}{dt} + \frac{ρ C_{D} A}{2} v^{2} (4) \end{matrix}$

式中: F_b为道路滚动阻力;则制动消耗的能量(kWh)为:

$\begin{matrix} E_{b} = \overset{t_{2}}{\sum_{t = t_{1}}} \frac{F_{b} v}{1000} Δt / 3600 (5) \end{matrix}$

又设整个行驶过程整车附件消耗功率(kW)为 P_a,则附件能耗(kWh)为:

$\begin{matrix} E_{a} = \overset{t_{2}}{\sum_{t = 0}} P_{a} Δt / 3600 (6) \end{matrix}$

总能耗为:

$\begin{matrix} E_{tal} = E_{t} / η_{m} η - E_{b} η_{b} + E_{a} (7) \end{matrix}$

式中: η_m为电动汽车传动系机械传动效率; η为电动效率,可以根据效率MAP图插值获得; η_b为电动汽车制动能量回收效率。

图1为车辆在长春市内某路上行驶的速度时间序列数据(数据时间长度约为1550 s)。车辆的能耗计算需要将上述数据带入式(7)进行逐点计算,通过累加单个数据点的能耗值,最后得到总的能耗,计算所需时间长。

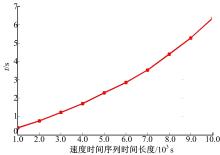
	Figure Option View Download New Window
	图1 车辆在长春市某路上行驶的速度时间序列数据Fig.1 Velocity time series data of car driving at one road in Changchun

为了分析模型计算对耗时的影响,作者对模型1000 s、2000 s、…、10000 s等10组不同时间长度的数据耗时进行了统计,每组时间长度选取12段不同的数据,并对其模型计算耗时求平均值,统计结果见图2。

	Figure Option View Download New Window
	图2 速度时间序列模型能耗计算的平均时间Fig.2 Average calculation time of velocity time series energy consumption model

从图2可以看到:时间长度越大,能耗计算时间越长,几乎成线性增长。无法满足电动汽车通过能耗实时计算来选择节能路径的需求,因此需要改进瞬时能耗计算模型,提高计算效率。

2 VA概率分布

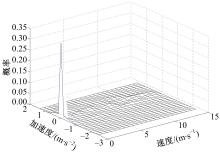
将汽车运行工况的速度时间序列进行一定的处理得到相关的加速度时间序列,然后将速度、加速度数据进行离散化处理^{[ 9]},计算每一段数据点的速度、加速度状态对应的概率,就得到了一个VA概率分布矩阵。VA概率矩阵反映了不同速度、加速度对应的状态所出现的概率,反映了汽车运行的状态特征。图3为长春市某道路上车辆行驶速度时间序列转换的VA概率分布矩阵的三维图。

	Figure Option View Download New Window
	图3 VA概率分布三维图Fig.3 The 3D map of VA probability distribution

由于城市汽车运行速度状态具有马尔可夫性^{[ 10]},而具有马尔可夫性的随机过程也同时满足遍历性^{[ 11]}。根据遍历性原理可以推出相关函数的时间平均等于统计平均^{[ 12, 13]}:

$\begin{matrix} \lim_{T \to \infty} \frac{1}{T} \int_{0}^{T} Q (t) dt = \int_{0}^{x} Q (x) p (x) dx (8) \end{matrix}$

式中: Q( t)为物理量 Q的时间序列; Q( x)为物理量 Q在相空间中的状态; p( x)为物理量 Q在相空间的概率密度(如果 Q为离散变量,则 p( x)为分布概率)。

根据上述分析,可以利用VA概率分布矩阵的统计平均替代速度时间序列的时间平均来用于车辆能耗的计算,这样可以解决已有能耗计算模型在进行大数据量计算时效率低的缺点。

3 能耗模型的建立

令速度时间序列中数据样本的个数为 n,速度单位为m/s,时间长度为 T,单位为s,VA概率矩阵为 C_M×N。

总功率(kW)等于每个速度状态点所求得的功率之和,即:

$\begin{matrix} P = \overset{n}{\sum_{k = 1}} P_{k} = \overset{n}{\sum_{k = 1}} (F_{k} v_{k} / 1000) (9) \end{matrix}$

式中: F_k为运用汽车行驶方程式得到的每个速度状态对应的行驶阻力,是速度 v_k和加速度d v_k/d t的函数。

此时每一个VA状态点的平均功率(kW)为:

$\begin{matrix} P_{ij}^{(1)} = F_{ij} v_{i} / 1000 (10) \end{matrix}$

式中: F_ij为不同VA状态下所求得的汽车行驶阻力。

则所有VA状态点功率的统计平均(数学期望)(kW)为:

$\begin{matrix} {\bar{P}}_{t} = \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} (F_{ij} v_{i} p_{ij} / 1000) (11) \end{matrix}$

根据遍历性的性质可知,功率的时间平均等于功率的统计平均,即:

$\begin{matrix} \frac{1}{n} \overset{n}{\sum_{k = 1}} (F_{k} v_{k} / 1000) = \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} (F_{ij} v_{i} p_{ij} / 1000) (12) \end{matrix}$

式(12)两边同时乘以 n,则变为:

$\begin{matrix} \overset{n}{\sum_{k = 1}} (F_{k} v_{k} / 1000) = \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} (F_{ij} v_{i} p_{ij} / 1000) n (13) \end{matrix}$

另外,由每个VA状态点的功率可知,在相同VA状态下的所有状态点的功率(同一个VA状态对应的点的个数有可能大于1,此时通过样本点的总数 n以及每个状态的分布概率 p_ij就可以求出每个状态中具体的样本点个数 np_ij)之和为:

$\begin{matrix} P_{ij} = P_{ij}^{(1)} p_{ij} n = F_{ij} v_{i} p_{ij} n / 1000 (14) \end{matrix}$

总的功率为:

$\begin{matrix} P_{t} = \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} (F_{ij} v_{i} p_{ij} / 1000) n (15) \end{matrix}$

由此可知,在速度时间序列具有遍历性的前提下,通过VA分布矩阵求得的总功率等于在速度时间序列中求得的总功率。能耗 E_t(kWh)为:

$\begin{matrix} \begin{matrix} E_{t} = \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} (F_{ij} v_{i} p_{ij} / 1000) n \frac{T}{n} \frac{1}{3600} \\ 即 : E_{t} = \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} (F_{ij} v_{i} p_{ij} / 1000) T \frac{1}{3600} (16) \end{matrix} \end{matrix}$

当驱动力大于或等于零时,汽车处于加速或匀速驱动状态,则驱动能耗为:

$\begin{matrix} \begin{matrix} E_{t} = \overset{M}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} ((mgf + δm \frac{d v_{i}}{dt} + \\ \frac{ρ C_{D} A}{2} v_{i}^{2}) \frac{v_{i} p_{ij}}{1000}) T \frac{1}{3600} (17) \end{matrix} \end{matrix}$

当驱动力小于零时,汽车处于减速制动状态,则制动能耗为:

$\begin{matrix} \begin{matrix} E_{b} = \overset{M}{\sum_{i = K}} \overset{N}{\sum_{j = 1}} ((mgf + δm \frac{d v_{i}}{dt} + \\ \frac{ρ C_{D} A}{2} v_{i}^{2}) \frac{v_{i} p_{ij}}{1000}) T \frac{1}{3600} (18) \end{matrix} \end{matrix}$

行驶过程中电动汽车附件能耗为:

$\begin{matrix} E_{a} = P_{a} \frac{T}{n} \frac{1}{3600} (19) \end{matrix}$

综合电动汽车驱动能耗、制动能耗和整车附件能耗,电动汽车在行驶过程中的总能耗可根据式(7)计算得到。

4 能耗模型计算结果分析

4.1 模型的计算时间

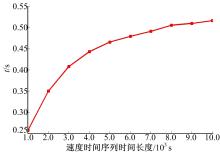
本文将VA概率矩阵划分状态设为90×90区间,使用前文所用的10组不同的时间长度数据,统计VA概率分布模型计算耗时长度,每组仍是计算12段不同数据所耗时间的平均值,统计结果如图4所示。

	Figure Option View Download New Window
	图4 VA能耗模型能耗计算的平均时间Fig.4 Average calculation time of VA energy consumption model

对比图2和图4可以看出:基于VA概率分布能耗模型所需计算时间明显减少,而且随着数据量的增加,能耗模型计算时间不会随着速度时间序列时间长度的增加而快速增加。主要原因是汽车运行状态是有限的,利用VA概率矩阵计算能耗主要就是根据汽车运行状态进行能耗计算,所以计算时间不会持续增加,特别在大数据量的能耗计算时,优势更加明显。

4.2 两种方法计算能耗的一致性

分别用已有的基于速度时间序列能耗模型和本文开发的VA概率能耗模型(VA矩阵状态划分为90×90)计算能耗,结果如图5所示。

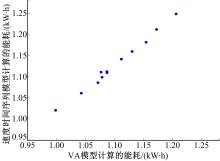	Figure Option View Download New Window
	图5 两种模型的能耗计算结果相关度分析Fig.5 Correlation analyse of calculation result from two energy consumption models

从图5可以看到:两模型计算结果相关度为99.64%,一致性较好。理论上,VA矩阵是由速度时间序列转化而成的,利用速度时间序列计算能耗与利用VA概率计算能耗计算结果应该一致,但由于速度时间序列数据离散化处理转化为VA状态矩阵过程中带有不可避免存在统计误差,以及计算能耗过程中根据插值方法计算电机效率存在的计算误差,这些误差导致了两类模型在实际计算中产生了不一致性。但从计算结果上看,相对误差是在一个可以接受的范围内,这就验证了理论上通过将速度时间序列转化为VA矩阵进行能耗计算的合理性。

4.3 能耗模型的试验验证

利用奔腾B50实车试验采集的电动汽车电机输入电流 I( t)、电压 U( t)以及车辆行驶的速度时间序列数据分别计算电动汽车的道路试验能耗和基于VA概率分布能耗模型的仿真能耗。数据的采集频率都为10 Hz。

由采集数据得到的电机输入功率(kW)为:

$\begin{matrix} P (t) = U (t) I (t) / 1000 (20) \end{matrix}$

当数据个数为 n时计算所得能耗为:

$\begin{matrix} E = \overset{n}{\sum_{i = 0}} [P (t) \times 0.1] / 3600 (21) \end{matrix}$

相对误差计算公式为:

$\begin{matrix} err = \frac{E_{M} - E_{test}}{E_{test}} \times 100 % (22) \end{matrix}$

式中: E_M为能耗模型仿真能耗; E_test为道路试验能耗。

根据式(20)(21)计算所得的道路试验能耗和能耗模型仿真能耗结果对比如图6所示,试验结果与模型仿真计算结果的相关度为93.74%,说明了能耗模型的计算结果比较准确。

	Figure Option View Download New Window
	图6 仿真能耗与试验能耗的相关度分析Fig.6 Correlation analyse between simulation of models and result of tests

5 结论

(1)采用新的建模思路,基于遍历性随机过程得到了电动汽车能耗的统计平均等于时间平均的特性,建立了基于VA概率分布的电动汽车能耗计算模型,大幅提高了以往利用速度时间序列计算能耗的时间效率。

(2)本文建立的能耗计算模型是根据汽车运行状态划分来计算能耗的。由于城市中汽车运行状态是有限的,这就使能耗模型计算时间不会随着数据量的增大而增加,大数据量计算时优势明显。

(3)VA概率能耗模型的能耗计算值与试验测试能耗值的相关度为93.74%,计算精度较高。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ahn K, Rakha H. The effects of route choice decisions on vehicle energy consumption and emissions[J]. Transportation Research Part D: Transport and Environment, 2008, 13(3): 151-167. [本文引用:1] [JCR: 1.291]
[2]	Assessment and stand ards division office of transportation and air quality US environmental protection agency. Updating fuel economy estimates in MOBILE6. 3[R]. US: EPA, 2002. [本文引用:1]
[3]	Ahn K, Rakha H, Trani A, et al. Estimating vehicle fuel consumption and emissions based on instantaneous speed and acceleration levels[J]. Journal of Transportation Engineering, 2002, 128(2): 182-190. [本文引用:1] [JCR: 0.863]
[4]	Gino S, Mark S B. Formulae for the tractive energy requirem-ents of vehicle driving the EPA schedules[C]//SAE Paper, 810184. [本文引用:1]
[5]	陈清泉, 孙逢春, 祝嘉光. 现代电动汽车技术[M]北京: 北京理工大学出版社, 2002. [本文引用:1]
[6]	Mehrdad E, Gao Y M, Ali E. 现代电动汽车、混合动力电动汽车和燃料电池车——基本原理、理论和设计[M]. 第2版. 倪光正, 倪培宏, 熊素铭译. 北京: 机械工业出版社, 2010. [本文引用:1]
[7]	王志新, 王军, 魏跃远. 基于行驶工况的电动车比能耗计算与分析[J]. 车辆与动力技术, 2005(4): 39-43. Wang Zhi-xin, Wang Jun, Wei Yue-yuan. Calculation and analysis of specific energy of EV based on running schedule[J]. Vehicle & Power Technology, 2005(4): 39-43. [本文引用:1]
[8]	余志生. 汽车理论[M]. 4版. 北京: 机械工业出版社, 2006. [本文引用:1]
[9]	刘丽. 轿车城区瞬态运行工况的组合设计方法研究[D]. 长春: 吉林大学交通学院, 2007. Liu Li. Title of dissertation: study on the combined design method of urban transient driving cycles for passenger car[D]. Changchun: College of Transportation, Jilin University, 2007. [本文引用:1]
[10]	张岩. 面向混合动力汽车能量管理策略的汽车运行工况多尺度预测方法[D]. 长春: 吉林大学交通学院, 2013. Zhang Yan. Multi-scale prediction method of driving cycle for HEV energy management strategy[D]. Changchun: College of Transportation, Jilin University, 2013. [本文引用:1] [CJCR: 0.1885]
[11]	盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 第三版. 北京: 高等教育出版社, 2001. [本文引用:1]
[12]	刘次华. 随机过程[M]. 第四版. 武汉: 华中科技大学出版社, 2008. [本文引用:1]
[13]	刘秉正, 彭建华. 非线性动力学[M]. 北京: 高等教育出版社, 2004. [本文引用:1]

2008

1.291

0.0

. 2008, 13(3):151-167 DOI:10.1016/j.trd.2008.01.005

The effects of route choice decisions on vehicle energy consumption and emissions

Abstract

Motorists typically select routes that minimize their travel time or generalized cost. This may entail traveling on longer but faster routes. This raises questions concerning whether traveling along a longer but faster route results in energy and/or air quality improvements. We investigate the impacts of route choice decisions on vehicle energy consumption and emission rates for different vehicle types using microscopic and macroscopic emission estimation tools. The results demonstrate that the faster highway route choice is not always the best from an environmental and energy consumption perspective. Specifically, significant improvements to energy and air quality can be achieved when motorists utilize a slower arterial route although they incur additional travel time. The study also demonstrates that macroscopic emission estimation tools (e.g., MOBILE6) can produce erroneous conclusions given that they ignore transient vehicle behavior along a route. The findings suggest that an emission- and energy-optimized traffic assignment can significantly improve emissions over the standard user equilibrium and system optimum assignment formulations. Finally, the study demonstrates that a small portion of the entire trip involves high engine-load conditions that produce significant increases in emissions; demonstrating that by minimizing high-emitting driving behavior, air quality can be improved significantly.

... 另一类为微观能耗计算模型^[1] ...

2002

0.0

... 宏观能耗计算模型主要是采用调查和统计的方法,通过采集和统计能耗数据得出一段时间内的汽车平均能耗数值,计算的时间尺度达到了月甚至年,主要的目的就是用来总体评价一段时间内汽车的平均能耗情况,具有代表性的模型为美国环保署开发的MOBILE6^[2] ...

2002

0.863

0.0

... 微观能耗模型主要分为两种:一种通过拟合方法建立汽车运行状态与能耗之间的关系,具有代表性的模型是美国弗吉尼亚理工大学交通系的Ahn和土木工程系的Rakha、Trani合作开发的VT micro model^[3] ...

0.0

... 另一种是通过整车动力学分析建立整车瞬时运行状态与能耗的关系,具有代表性的模型是美国通用汽车研究实验室Gino和Mark的基于车辆运行工况速度时间序列的汽车能耗计算模型^[4] ...

2002

0.0

... 由于电动汽车和传统燃油汽车在动力学分析上没有本质区别^[5],以动力学分析为基础建立的电动汽车能耗模型的分析方法与传统燃油汽车差别很小,因此本文方法也适用于传统燃油汽车 ...

2010

0.0

2006

0.0

... 已知汽车行驶方程式^[8]: ...

2007

0.0

... 2 VA概率分布将汽车运行工况的速度时间序列进行一定的处理得到相关的加速度时间序列,然后将速度、加速度数据进行离散化处理^[9],计算每一段数据点的速度、加速度状态对应的概率,就得到了一个VA概率分布矩阵 ...

2013

0.0

0.1885

... 由于城市汽车运行速度状态具有马尔可夫性^[10],而具有马尔可夫性的随机过程也同时满足遍历性^[11] ...

2001

0.0

... 由于城市汽车运行速度状态具有马尔可夫性^[10],而具有马尔可夫性的随机过程也同时满足遍历性^[11] ...

2008

0.0

2004

0.0