高速公路交通流运行稳定性分析

引用本文

杨庆芳, 马明辉, 杨聚芬, 邴其春, 梁士栋. 高速公路交通流运行稳定性分析. 44(6): 1596-1603
YANG Qing-fang, MA Ming-hui, YANG Ju-fen, BING Qi-chun, LIANG Shi-dong. Analysis of the traffic flow operating stability on highway. Journal of Jilin University Engineering and Technology Edition, 44(6): 1596-1603 复制到剪切板

Permissions

高速公路交通流运行稳定性分析

杨庆芳^1,², 马明辉², 杨聚芬², 邴其春², 梁士栋²

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.吉林大学交通学院,长春 130022

通信作者:马明辉(1989-),女,博士研究生.研究方向:高速公路可变限速控制,交通诱导.

作者简介:杨庆芳(1966-),女,教授,博士生导师.研究方向:智能交通运输系统.E-mail:yangqf@jlu.edu.cn

基金:“863”国家高技术研究发展计划项目(2012AA112307);

摘要

为了提升高速公路限速值设置的可信度,确保速度控制方法选择的合理性,从高速公路交通流运行的时间特性和空间特性角度出发,对单截面和双截面采集的交通流参数数据进行分析,分别构建了以速度差为基础的稳定性分析模型,并进行优化组合,提出了高速公路交通流稳定性识别方法。采用山东某高速公路微波实测数据和VISSIM微观仿真软件对其进行实证分析,结果表明:高速公路交通流稳定性识别方法能够高效地识别出道路交通流的离散度,并能够定量地、较好地描述交通流运行的稳定性,从而为高速公路的动态限速管理及限速值的确定提供可靠的决策依据。

关键词: 交通运输系统工程; 高速公路; 稳定性分析; 动态限速; 速度差

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2014)06-1596-08

Analysis of the traffic flow operating stability on highway

YANG Qing-fang^1,², MA Ming-hui², YANG Ju-fen², BING Qi-chun², LIANG Shi-dong²

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022,China

2.College of Transportation, Jilin University, Changchun 130022,China

Abstract

In order to enhance the credibility of the highway speed limit setting and ensure reasonable selection of speed control method, this paper analyzes the traffic flow data collected by single section and double section. The analysis is from the perspective of spatial and temporal characteristics of highway. Then three stability analysis models are constructed, which treat speed difference as the main research focus. Further, a recognition method of traffic flow stability is presented. The three new models are verified with the microwave monitoring data on a highway in Shandong province using WISSIM simulation software. The results show that identification model of traffic flow stability can identify the dispersion of traffic flow and describe the stability of traffic flow efficiently, which will provide reliable decision basis for highway management of dynamic speed limits.

Keyword: engineering of communications and transportation system; freeway; stability analysis; dynamic speed limit; velocity difference

Show Figures

高速公路动态限速管理是解决高速公路事故频发问题的有效手段。与传统限速不同,动态限速是根据道路动态信息对限速值进行约束^{[ 1]}。根据应用方法不同,动态限速控制模型主要包括以交通流理论为基础的动态限速模型^{[ 2, 3, 4]}、以人工智能算法为基础的动态限速模型^{[ 5, 6, 7]}等。但在各种模型中对于高速公路在何种条件或状态下进行动态限速控制的研究却非常少。道路环境状态的识别关系到动态限速值确定的合理性,直接影响着交通流运行的安全和效率^{[ 8]}。因此,本文从单、双截面交通流运行特性问题入手,分别设计了以速度差为基础的单、双截面交通流离散度分析模型,并以此为基础提出了一种高速公路主线路段交通流稳定性分析方法,以提高动态限速值的可靠性,为高速公路动态限速管理提供实时、准确的决策依据。

1 动态限速前期预判基本思路

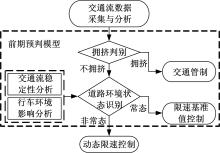
高速公路动态限速控制前期预判主要思路是根据在线采集的实时交通流参数数据,进行实时交通流拥挤判别,再通过道路环境状态识别模型对交通流参数数据进行二次识别,进而确定交通流运行的稳定程度。

高速公路动态限速控制前期预判方法主要包括拥挤判别和道路环境状态识别两部分。研究的主要技术路线如图1所示。

	Figure Option View Download New Window
	图1 高速公路动态速度控制技术路线Fig.1 Technical route of highway dynamic speed control

拥挤判别的目的是为交通决策提供必要的支持^{[ 9]}。如一旦发现交通拥挤,交通管理部门能依据判别结果及时采取措施,疏导交通流^{[ 10]}。目前,国内外学者已经针对高速公路拥堵识别问题进行了大量的研究,交通拥挤判别相关研究成果已较为成熟^{[ 11, 12]},因此,本文将不再对交通拥挤模型进行研究。

与交通状态判别不同,道路环境状态识别主要包括交通流稳定性和道路环境(天气、路边环境等)状态识别两部分。道路环境状态识别的主要目的是识别不同交通情境下的交通流运行的稳定程度,进而为动态限速值的设置提供依据。由于道路环境状态判别存在着巨大的研究空间,且道路环境状态信息很难量化,因此,本文将道路环境状态判别中交通流稳定性分析作为重点研究内容。

2 交通流稳定性分析方法设计

为了提高动态限速模型的鲁棒性,分别从交通流的时间特性和空间特性出发,提出高速公路交通流稳定性分析(Stability analysis of traffic flow,SATF)算法。SATF模型主要描述为在满足高速公路限速基准值要求的前提下,根据相应的算法模型对单截面和双截面采集的数据进行融合处理,从而对高速公路交通流稳定性进行分析。

2.1 限速基准值的确定

限速基准值 V₀指的是理想条件下车辆通过道路平直路段的运行速度,其中理性条件包括良好的路面条件、最佳的天气状况、自由流状态等。但由于不同道路线形条件下驾驶速度会有所不同,显然,对所有道路应用统一的限速标准是不合理的。因此,应根据具体检测路段车辆行驶速度的历史数据确定该路段的限速基准值,作为该路段车辆驾驶的极限限速值。本文参考文献[13]将调查路段正常交通状态条件下的85%分位和15%分位速度作为检测路段的最高和最低限速基准值,分别表示为 V_0(85%)和 V_0(15%),其所构成的限速范围( V_0(15%),V_0(85%))表示为R。

2.2 单截面稳定性分析模型

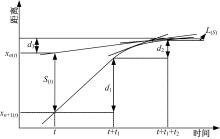
单截面采集的交通流参数数据能够有效地反应高速公路交通流的时间特性及运行的紧密程度,因而结合单检测器采集的数据进行限速前期状态判别具有重要意义。根据单截面采集的交通流数据特点,本文从交通流的时间序列差异的角度出发,对NEWELL提出的低阶跟驰模型^{[ 14]}进行改进,将单体车辆绝对静止跟驰模型扩展为以时间群为研究对象的车辆相对静止交通流稳定性分析模型,并定义为单截面稳定性分析(Single-section stability analysis,S-SA)模型,单截面交通流运行示意图如图2所示。

	Figure Option View Download New Window
	图2 单截面交通流运行示意图Fig.2 Single section traffic state diagram

由图2可以看出,在 t时刻 n+1车和前方相邻车辆 n车的车头时距为 S₍ _t₎,即 S₍ _t₎ =( x_n₍ _t₎ -x_n+₁₍ _t₎)。当 n+1车感知到前方 n车速度较慢或持续减速时,在无法换道超车的情况下,为了确保驾驶安全,便需要采取制动措施进行减速,此过程主要包括驾驶员反应阶段和制动阶段。由图2可知, d₁为反应时间 t₁内 n+1车行驶的距离,根据经验取 t₁ =2 .5 s; d₂为 n+1车在时间 t₂内驶过的距离。当 n+1车的车速和 n车车速基本保持一致时,两车将保持一定的距离继续行驶,两车行驶的最小安全距离为 L( s)。与此同时, n车继续以原有的速度行进,且在时间( t₁ +t₂)内的行驶距离为 d₃。进一步分析可知:

$\begin{matrix} d_{1} + d_{2} + L (s) - d_{3} \leq x_{n} (t) - x_{n + 1} (t) = S_{(t)} (1) \end{matrix}$

式中: d₁为识别距离:

$\begin{matrix} d_{1} = v_{n + 1} (t) \cdot t_{1} (2) \end{matrix}$

d₂为制动距离:

$\begin{matrix} d_{2} = \frac{{v_{0}}^{2} - v_{n + 1} {(t)}^{2}}{2 a} = \frac{{v_{0}}^{2} - v_{n + 1} {(t)}^{2}}{2 g \cdot (f - i)} (3) \end{matrix}$

d₃为 n车行驶距离:

$\begin{matrix} \begin{matrix} a t_{2} = (v_{n + 1} (t) - v_{0}) \\ d_{3} = (t_{1} + t_{2}) \cdot v_{n} (t) = t_{1} \cdot v_{n} (t) + \\ \frac{v_{n + 1} (t) - v_{0}}{g \cdot (f - i)} \cdot v_{n} (t) (4) \end{matrix} \end{matrix}$

式中: a为 n+1车的制动减速度; g为重力加速度,取值9.8 m/s²; f为地面摩擦因数; i为道路坡度, i=h/l,其中上坡取 +i,下坡取 -i; t₂为车辆制动速度降到 v₀的时间; v₀为( t+t₁ +t₂)时刻 n+1车的速度, v₀≤ v_n。

将式(2)~(4)带入式(1)中可知:

$\begin{matrix} \begin{matrix} v_{n + 1} (t) \cdot t_{1} + \frac{{v_{0}}^{2} - v_{n + 1} {(t)}^{2}}{2 g \cdot (f - i)} + L (s) - t_{1} \cdot v_{n} (t) + \\ \frac{v_{n + 1} (t) - v_{0}}{g \cdot (f - i)} \cdot v_{n} (t) \leq S_{(t)} (5) \end{matrix} \end{matrix}$

将已知基本参数 t₁ =2 .5 s, g=9 .8 m/s²带入公式(5)中,同时将基本单位换算为m和s,即可得到S-SA模型计算公式:

$\begin{matrix} \begin{matrix} Δv \leq \sqrt[]{{[88 (f - i)]}^{2} + 254 (f - i) (S_{(t)} - L (s))} \\ - 88 (f - i) Δv = (v_{n + 1} (t) - v_{n} (t)) (6) \end{matrix} \end{matrix}$

根据历史数据对单截面的速度离差阈值 K进行标定,即 Δv≤ K,对单截面的交通流运行的离散程度进行识别。

2.3 双截面稳定性分析模型

交通流理论中常采用平均速度差^{[ 15]}(统计时段内单车道车流中连续通过截面的相邻车辆速度差绝对值的均值)对交通流的离散性进行描述,其主要依靠单截面检测数据对交通流的运行特性进行分析,偏向于反映车辆时间序列上的交通流分布情况,导致对交通流运行特性的分析比较单一、研究范围受限,并且无法在空间位置上对交通流运行的差异进行分析。而依靠双截面检测获取的数据信息稳定性较强,能够高质量地获得两检测截面交通流运行特征数据。因此,本文在考虑交通流空间运行特性的基础上,提出了一种新的离散度指标计算方法,即将双截面实时采集到的交通流参数数据同历史数据相结合,并应用时间窗对历史数据进行动态更新,为模型应用提供必要的历史数据支持,定义该模型为双截面稳定性分析(Dual-section stability analysis,D-SA)模型。

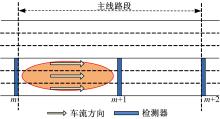
多截面检测路段示意图如图3所示,本文采用 m及 m+1截面间的路段进行双截面交通流稳定性分析。由于检测器的布设间距直接影响到D-SA模型的精度,如检测器之间布设间距过小将会导致通过两截面的车辆速度无明显差异,而检测器布设间距过大可能导致通过两截面的交通流状态截然不同,便缺乏了可对比性,因此,本文根据式(7)对连续截面间的布设间距进行设置:

$\begin{matrix} S_{\max} = \frac{v_{\max}^{2} - v_{\min}^{2}}{2 \min (a_{br}, a_{su})} (7) \end{matrix}$

式中: S_max为连续两截面布设的最大间距; a_br、 a_su分别为车辆最大制动减速度和启动加速度; v_max, v_min分别为路段上车辆行驶的最大速度和最小车速(一般为0)。

	Figure Option View Download New Window
	图3 多截面检测路段示意图Fig.3 Multi-section detection sections diagram

将采集间隔内通过观测地点 m及 m+1截面的车辆分别取平均值并取其差值,进而通过对历史数据纵向时间序列的计算得到两观测点历史速度离差(历史数据以5个窗体为单位,实时更新),取二者比值作为两相邻观测点对应采样间隔内交通流离散度指标,计算公式为:

$\begin{matrix} l_{i} = \frac{|{\bar{v}}_{m} (i) - {\bar{v}}_{m + 1} (i)|}{b + \frac{1}{n} \overset{n}{\sum_{k = 1}} |{\bar{v}}_{mi} (j) - {\bar{v}}_{(m + 1) i} (j)|} (8) \end{matrix}$

式中: $\begin{matrix} {\bar{v}}_{m} \end{matrix}$ ( i)为截面 m在第 i个采样间隔内的车辆速度均值; n为采用正常条件下历史数据的个数; b=0 .0001为防止分母为零而设定的极小定值; $\begin{matrix} {\bar{v}}_{mi} \end{matrix}$ ( j)为截面 m在 j时段的第 i个采样间隔内车辆速度均值,其中 j为历史数据采样时间段的分布。

在正常交通流条件下, | $\begin{matrix} {\bar{v}}_{m} \end{matrix}$ ( i) - $\begin{matrix} {\bar{v}}_{m + 1} \end{matrix}$ ( i) |在比较稳定的范围内波动,定义波动范围为 Q。由于在两检测地点处车辆到达率相对独立, Y_n服从二项分布,则:

$\begin{matrix} Y_{n} = \{\begin{matrix} 0, |{\bar{v}}_{m} (i) - {\bar{v}}_{m + 1} (i)| \notin Q \\ 1, |{\bar{v}}_{m} (i) - {\bar{v}}_{m + 1} (i)| \in Q \end{matrix}, X_{n} = \overset{N}{\sum_{n = 1}} Y_{n} (9) \end{matrix}$

式中: X_n表示在 N个检测数据中测得 $\begin{matrix} |{\bar{v}}_{m} (i) - {\bar{v}}_{m + 1} (i)| \end{matrix}$ 在范围 Q内出现的频次,显然 X_n是个随机变量且每次检测数据之间的关系式相互独立,故有:

$\begin{matrix} \begin{matrix} E [X_{N}] = E [Y_{1} + Y_{2} + \dots + Y_{N}] = E (Y_{1}) + \\ E (Y_{2}) + \dots + E (Y_{N}) = Np (10) \\ D [X_{N}] = D [Y_{1} + Y_{2} + \dots + Y_{N}] = D (Y_{1}) + \\ D (Y_{2}) + \dots + D (Y_{N}) = Np (1 - p) (11) \end{matrix} \end{matrix}$

显然,本文提出的离散度指数精度取决于 D $\begin{matrix} [\frac{X_{N}}{N}] \end{matrix}$ ,其表达式如下:

$\begin{matrix} D [\frac{X_{N}}{N}] = \frac{1}{N^{2}} Np (1 - p) = \frac{1}{N} p (1 - p) (12) \end{matrix}$

随机变量 X_N/N服从二项分布,则由de Moivre-Laplace中心极限定理^{[ 16, 17]}可知:

$\begin{matrix} \lim_{N \to \infty} P \{\frac{(\frac{X_{N}}{N}) - p}{\sqrt[]{D [\frac{X_{N}}{N}]}} \leq I\} = \int_{{-∞}_{}}^{I_{}} \frac{1}{\sqrt[]{2 π}} e^{- \frac{1}{2} μ^{2}} dμ (13) \end{matrix}$

当 N充分大时,则有 W= $\begin{matrix} \frac{(\frac{X_{N}}{N}) - p}{\sqrt[]{D [\frac{X_{N}}{N}]}} \end{matrix}$ 服从 N(0,1)标准正态分布,因此:

$\begin{matrix} \begin{matrix} P \{|\frac{(\frac{X_{N}}{N}) - p}{\sqrt[]{D [\frac{X_{N}}{N}]}}| \leq W_{1 - α / 2}\} = \\ P \{(\frac{X_{N}}{N}) - p \leq W_{1 - α / 2} \sqrt[]{D [\frac{X_{N}}{N}]}\} = 1 - α (14) \end{matrix} \end{matrix}$

式中:1 -α为置信度; W₁ _-α/₂为置信度为1 -α的正态分布临界值。

新的离散度指标具有明显的物理意义,其反映了相邻检测器交通流运行速度的相互关系,从空间角度上将交通流平稳性进行量化,为交通流状态识别提供了空间识别支持。

3 SATF算法基本流程

SATF算法是指在限速基准值约束的前提下,通过对单、双检测截面的优缺点分析,将S-SA模型与D-SA模型融合,并通过对交通流参数数据的计算,对高速公路检测区域交通流运行稳定性进行识别。

$\begin{matrix} ψ = \{\begin{matrix} 0, 交通流不稳定 \\ 1, 交通流稳定 \end{matrix} (15) \end{matrix}$

图3为高速公路主线示意图, m截面至 m+1截面为交通流平稳性检测区域,车流方向为 m截面至 m+1截面方向,以该图为例说明本文设计的SATF算法的基本流程:

(1)当 m(或 m+1)检测地点采集到的速度 v连续多次超出相应检测地点的阈值范围R _m(或R _m+₁)时, ψ=0,截面的交通流处于不稳定状态,则执行步骤(4);否则执行步骤(2)。根据车流运行特征及S-SA模型分析的要求,将 m截面归属于本检测路段,而 m+1截面则归属于下一检测路段。

(2)根据S-SA模型对在检测路段起始点,即 m截面采集到的交通流参数数据进行计算,判断截面车速的离散程度。当连续出现 Δv≤ K时,不对其进行任何处理,同时对历史数据进行更新,阈值更新,执行步骤(3);否则当连续多次出现 Δv>K时,则 ψ=0,截面的交通流处于不稳定状态,执行步骤(4)。

(3)根据D-SA模型对 m截面和 m+1截面采集的交通流参数数据进行融合计算。当连续多次出现 l_i≤ l_标时,执行步骤(5);否则执行步骤(4)。

(4)根据检测路段的交通流运行情况及道路环境对其实施动态限速值控制。

(5)对两截面的基准限速值进行加权平均计算,设置区域静态限速值。

算法流程中需要对阈值进行多次判断,研究表明一般选取连续3次作为判别依据。

4 实证分析

4.1 方案设计

试验方案设计主要分为两部分:第一部分是通过应用山东省某高速公路实测数据对SATF模型对交通流变稳定性识别的敏感度进行分析校验;第二部分则采用文献[18]提出的可变限速模型并通过VISSIM微观仿真软件对检测路段车辆的尾气排放量、速度及行程时间等指标进行输出,进而对SATF模型的实效性进行验证。

(1)SATF模型敏感度分析

敏感度分析采用的实证数据来源于山东省某高速公路主线路段的微波检测器。用 m截面和 m+1截面正常交通状态下采集到的5个星期的周一数据(如表1)作为历史数据,采用2011年10月29日和2011年11月12日存在异常交通状况的两个周一交通流数据作为测试数据,分别标记为A组和B组,其中将A组数据和B组数据中在 m截面采集到的数据分别标记为A _m组和B _m组。

(2)SATF模型实效性验证

文献[18]根据高速公路动态限速控制是一个非线性时变系统这一特点,提出了基于神经网络控制模型优化的动态限速值方法,并对其进行分析研究,验证了方法的可行性,并得到广泛的应用。因此,本文将该方法和VISSIM微观仿真软件相结合对SATF模型的实效性进行验证分析。验证方案选取两种方案对比分析模式,其中方案一为应用SATF模型的动态限速控制路网仿真;方案二为不应用SATF模型的动态限速控制路网仿真,两种方案采取同样的路网设置和基本参数设置。

表1 正常交通流参数5 min合成数据部分示例 Table 1 Normal traffic flow parameters 5 minutes synthetic data part of the sample

为了更直观地表现应用SATF模型对动态速度控制的影响,利用VISSIM微观仿真软件对其进行模拟。仿真环境:良好天气状况下高速公路双向四车道的平直路段,路段长度为1 km,假设在700 m处有交通事故发生。交通组成选用小汽车、大客车及货车,比例分别为80%,15%及5%。由于VISSIM仿真软件中车辆的到达成随机分布,故仿真5次,每次的随机种子取值分别为42、47、58、64和69。

每次仿真时间为1800 s,时段0~600 s输入交通量为1200 pcu/h(约为路段两车道通行能力的30%);时段600~1200 s输入交通流量为2400 pcu/h(约为路段两车道通行能力的60%),时段1200~1800 s输入交通流量为1200 pcu/h。

4.2 试验效果分析

通过对 m截面和 m+1截面的历史数据进行计算,得到 m截面和 m+1截面的最高、最低限速基准值,如表2所示。

表2 m截面和 m+1截面最高、最低限速基准值 Table 2 Maximum and minimum speed reference value on m section and m+1 section

由表2可知, m截面和 m+1截面限速基准值分别为(60,120)和(65,115),根据限速范围对历史数据和测试数据进行筛选:对于历史数据需剔除不满足条件的数据,剩余数据用于后续模块的应用分析;对于实测数据连续多次超出限速范围的情况,则采用动态限速值进行控制,反之剩余数据进行下一模块的应用分析。

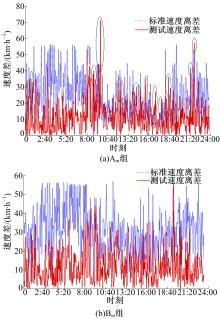
根据式(6)对在A组、B组的 m截面采集的数据进行计算分析,得出不同车间距条件下对速度离差的限制要求,如图4所示。

	Figure Option View Download New Window
	图4 A _m组和B _m组测试数据分析图Fig.4 A _m and B _m group of test data analysis diagram

从图4(a)可以看出,A _m组测试数据的速度离差与相同时刻的标准速度离差相比波动较大,其中椭圆形标记处表示数据的测试速度离差超出标准速度离差范围,不能满足安全行车的要求。对应表3可知,在时间段9∶42~9∶52内,A _m组数据的测试速度离差连续4次超出标准速度离差,说明此状态非偶然现象,因此,需要对 m截面进行应急管理,建议直接对 m截面采用动态限速控制,以确保交通流安全、稳定运行。

表3 A _m组部分测试数据 Table 3 A _m group of partial test data

从图4(b)可以看出,相对于A _m组测试数据,B _m组测试数据波动幅度较为缓和,测试速度离差基本上保持在标准速度离差范围内波动。但针对B _m组测试数据的分析结果只能用于对 m截面附近小范围内的交通流变化情况进行判断,无法对检测区域内道路环境状态进行识别,因此,需对B组 m截面和 m+1截面采集的数据进行二次识别。

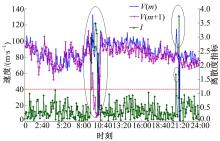
通过对历史数据计算分析,确定当交通流处于稳定的状态下时, l_标值在(0,1.14)之间波动,当交通流处于不稳定状态时其波动幅度较大。根据式(9)~(14)计算得知,当 l_标值处于(0,1.14)之间波动时,其置信度为0.95,试验的精度 $\begin{matrix} |\frac{X_{N}}{N} - p| \end{matrix}$ 达到0.001。由此可以说明,D-SA模型能够有效地检测出两检测地点采集数据的离散程度。

根据式(8)对B组测试数据进行计算分析,得到对应时间点的离散度指标,部分示例如表4所示。将获得的离散度指标与标准离散度指标进行对比分析,如图5所示。

表4 部分异常数据和正常数据对比分析示例表 Table 4 Comparative analysis of abnormal data and normal data sample table

从表4可以看出,异常数据示例中显示的 m截面和 m+1截面的检测速度离差较大,对应的 l_i数值也超出了标准离散度指数范围,而正常数据示例中显示的 m截面和 m+1截面的检测速度离差变化较小,对应的 l_i数值均在标准离散度指数变化范围内波动。异常数据示例同正常数据示例相比,其速度离差变化浮动较大,对应的离散度指标对比变化较为显著(超出标准波动范围)。

从图5中可以看出,本文提出的离散度指标同两截面速度的离散程度变化是相互对应的。当离散度指标处于标准阈值范围内时两截面速度的离差变化较小;当离散度指标出现越界时两截面速度的离差变化较大。在9∶00~10∶15时间段内测试数据的离散度指标 l连续多次超出标准阈值范围,此时交通流处于不稳定状态,道路安全受到威胁,因此需要根据实际的路况采用动态限速控制设置动态限速值对交通流速度进行限制;在11∶00~20∶00时间段内测试数据的离散度指标 l波动比较稳定,基本保持在标准阈值范围内,因此应根据实际路况选择动态限速控制设置固定限速值(限速基准值)进行交通流速度控制。

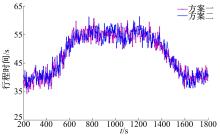
	Figure Option View Download New Window
	图5 双截面数据分析Fig.5 Double interfacial data analysis

通过VISSIM微观仿真软件得到方案一和方案二对环境的影响(CO,CO₂排放量)、平均速度、燃油消耗及行程时间的对比分析情况,如表5和图6所示。

表5 两种方案的CO,CO₂排放量 Table 5 Two schemes of CO,CO₂ emission comparison

	Figure Option View Download New Window
	图6 两种方案的行程时间对比分析图Fig.6 Schemes of travel time comparison

道路行车驾驶中高频的加速或减速行为会导致燃油消耗增加,尾气排放量的增加也会使环境的污染程度加重。由表5可以看出,方案一中的CO、CO₂排放量及燃油消耗低于方案二中的各对应指标。虽然各项指标从数值上相对变化幅度较小(波动幅度为1.5%~2.5%),但相关研究表明^{[ 18]},汽车尾气中含有CO、CO₂及有害颗粒等对人体及环境的危害极大。因此综合分析各项影响因素,实施方案一比实施方案二更具有优势。

由图6可以看出,相对方案二而言,方案一中动态限速的实施使得车辆平均速度降低,因此同样的行车里程应需要花费较长的行程时间。然而两种方案的行程时间并没有较大的变化,均具有相同的变化趋势,数值也极为相近。产生这种现象的原因最大可能是方案二中交通流运行的速度变化率较大,也就是说方案二中车辆加速和减速行为较为频繁,交通流的波动性较大。因此,应用SATF模型的方案一更加具有现实意义,起到了平稳交通流,提高交通运行安全的效用。

5 结束语

针对高速公路动态限速前期状态识别问题,从速度离差角度出发,对道路交通流的运行状态进行了稳定性分析,确保动态限速控制限速值选取的合理性。采用山东某高速公路微波实测数据及VISSIM微观仿真模型,对提出的SATF模型进行了分析验证,结果表明,SATF模型能够有效地检测交通流运行的离散度,并能够较好地描述交通流运行的稳定性,进一步提高了高速公路动态限速控制限速值选取的准确性和可靠性,为高速公路管理部门提供了较好的决策依据。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Elvik R. A restatement of the case for speed limit[J]. Transport Policy, 2010, 17(3): 196-204. [本文引用:1]
[2]	Carlson R C, Papamichail I, Papageorgiou M. Local feedback-based mainstream traffic flow control on motorways using variable speed limits[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(4): 1261-1276. [本文引用:1] [JCR: 3.064]
[3]	Kang K P, Chang G L, Zou N. Optimal dynamic speed-limit control for highway work zone operations[J]. Transportation Research Record: Journal of the Transportation Research Board, 2004, 1877(1): 77-84. [本文引用:1]
[4]	干宏程, 孙立军. 高速公路可变限速控制技术研究[J]. 交通科技, 2004(6): 91-93. Gan Hong-cheng, Sun Li-jun. A study on the variable speed limits technology for freeway[J]. Transportation Science & Technology, 2004(6): 91-93. [本文引用:1]
[5]	Chien C C, Ioannou P, Chu C K. Fuzzy traffic density homogenizer for automated highway system[C]∥Fuzzy Systems, 1994, IEEE World Congress on Computational Intelligence, Proceedings of the Third IEEE Conference on. IEEE, 1994: 968-973. [本文引用:1]
[6]	程国柱. 高速道路车速限制方法研究[D]. 哈尔滨: 哈尔滨工业大学交通科学与工程学院, 2007. Cheng Guo-zhu. Research on the method of setting speed limits on freeway and urban expressway[D]. Harbin: Harbin Institute of Technology, School of Transportation Science and Engineering, 2007. [本文引用:1]
[7]	陈大山. 高速公路主线可变限速控制研究[D]. 西安: 长安大学电子与控制工程学院, 2009. Chen Da-shan. Research on variable speed control for Freeway[D]. Xi'an: Chang'an University, College of Electronics and Control Engineering, 2009. [本文引用:1]
[8]	隽志才, 姚宏伟, 贾洪飞, 等. 高速公路可变限速系统的社会经济影响评价[J]. 公路交通科技, 2004, 21(5): 104-108. Juan Zhi-cai, Yao Hong-wei, Jia Hong-fei, et al. Expressway socio-economic impact assessment for variable speed limits[J]. Journal of Highway and Transportation Research and Development, 2004, 21(5): 104-108. [本文引用:1] [CJCR: 0.844]
[9]	De Palma A, Lindsey R. Traffic congestion pricing methodologies and technologies[J]. Transportation Research Part C: Emerging Technologies, 2011, 19(6): 1377-1399. [本文引用:1] [JCR: 2.006]
[10]	Arnott R. A bathtub model of downtown traffic congestion[J]. Journal of Urban Economics, 2013, 76: 110-121. [本文引用:1]
[11]	Lu Jia, Cao Li. A quantization method of traffic congestion evaluation based on fuzzy logic[C]∥IEEE International Conference on System, Man & Cybernetics, Washington DC, USA, 2003: 3348-3351. [本文引用:1]
[12]	Kerner B S. Synchronized flow as a new traffic phase and related problems for traffic flow modeling[J]. Mathematical and Computer Modeling, 2002, 35(5-6): 481-508. [本文引用:1]
[13]	贺玉龙, 孙小端. 公路速度限制与速度控制技术[M]. 北京: 人民交通出版社, 2011. [本文引用:1]
[14]	Newell G F. A simplified car-following theory: a lower order model[J]. Transportation Research Part B: Methodological, 2002, 36(3): 195-205. [本文引用:1] [JCR: 2.944]
[15]	Wang H, Wang W, Chen X W, et al. Experimental features and characteristics of speed dispersion in urban freeway traffic[J]. Transportation Research Record: Journal of the Transportation Research Board, 2007, 1999(1): 150-160. [本文引用:1]
[16]	Dedecker J. A central limit theorem for stationary rand om fields[J]. Probability Theory and Related Fields, 1998, 110(3): 397-426. [本文引用:1] [JCR: 1.394]
[17]	Lai T L, Qian L F, Shao Q M. Asymptotic Theory in Probability and Statistics with Applications[M]. Beijing: Higher Education Publishing House, 2007. [本文引用:1]
[18]	Lee C, Hellinga B, Saccomanno F. Evaluation of variable speed limits to improve traffic safety[J]. Transportation Research Part C: Emerging Technologies, 2006, 14(3): 213-228. [本文引用:1] [JCR: 2.006]

2010

0.0

. 2010, 17(3):196-204 DOI:10.1016/j.tranpol.2009.12.006

A restatement of the case for speed limit

Abstract

This paper provides a restatement of the case for speed limits. The paper argues that driver speed choice cannot be granted any normative status (i.e. be regarded as optimal from a societal point of view) unless it is “objectively” rational, even if it can be reasonably interpreted as “subjectively” rational. A distinction between “subjective” and “objective” rationality is very rarely made in modern analyses relying on the theory of rational choice, but it makes sense with respect to the choice of speed. Studies that have assessed which impacts of speed drivers consider, whether drivers correctly assess these impacts, and how drivers coordinate their choice of speed with other drivers are reviewed. It is concluded that driver speed choice is not “objectively” rational. It is concluded that the lack of rationality in driver speed choice implies that this choice needs to be regulated by means of speed limits.

... 与传统限速不同,动态限速是根据道路动态信息对限速值进行约束^[1] ...

2011

3.064

0.0

2004

0.0

1994

0.0

2007

0.0

2009

0.0

2004

0.0

0.844

. 2004, 21(5):104-108

Expressway socio-economic impact assessment for variable speed limits

运用计算机对高速公路典型路段可变限速系统进行模拟,模拟结果表明在交通量等于或大于2800veh/h出现明显的效益.根据行程时间和实际服务流量确定不同交通量情况下可变限速的最佳值,并基于行程时间的节省测度出各交通量条件下实施可变限速货币化的增量效益,进行了成本效益分析.采用DEA方法进行多目标综合评价,评价结果显示,在DEA的各方案中3200、3400、3600、3800veh/h所对应的DMU是DEA有效的.本文还证明了DEA对ITS项目评价是很有适用价值的,它能够描述用货币单位难以测度,但可用某种定量指标表述的重要影响.

... 道路环境状态的识别关系到动态限速值确定的合理性,直接影响着交通流运行的安全和效率^[8] ...

2011

2.006

0.0

. 2011, 19(6):1377-1399 DOI:10.1016/j.trc.2011.02.010

Traffic congestion pricing methodologies and technologies

Abstract

This paper reviews the methods and technologies for congestion pricing of roads. Congestion tolls can be implemented at scales ranging from individual lanes on single links to national road networks. Tolls can be differentiated by time of day, road type and vehicle characteristics, and even set in real time according to current traffic conditions. Conventional toll booths have largely given way to electronic toll collection technologies. The main technology categories are roadside-only systems employing digital photography, tag & beacon systems that use short-range microwave technology, and in-vehicle-only systems based on either satellite or cellular network communications. The best technology choice depends on the application. The rate at which congestion pricing is implemented, and its ultimate scope, will depend on what technology is used and on what other functions and services it can perform.

Highlights

? This paper reviews the methods and technologies for congestion pricing of roads. ? Tolling schemes range in scale from individual lanes to national road networks. ? The main technology options use cameras, transponders, satellites & cellular networks. ? The best scale depends on what other functions the technology can perform.

... 拥挤判别的目的是为交通决策提供必要的支持^[9] ...

2013

0.0

. 2013, 76:null-null

A bathtub model of downtown traffic congestion

... 如一旦发现交通拥挤,交通管理部门能依据判别结果及时采取措施,疏导交通流^[10] ...

2003

0.0

2002

0.0

. 2002, 35(5-6):null-null

Synchronized flow as a new traffic phase and related problems for traffic flow modeling

2011

0.0

2002

2.944

0.0

. 2002, 36(3):null-null

A simplified car-following theory: a lower order model

... 根据单截面采集的交通流数据特点,本文从交通流的时间序列差异的角度出发,对NEWELL提出的低阶跟驰模型^[14]进行改进,将单体车辆绝对静止跟驰模型扩展为以时间群为研究对象的车辆相对静止交通流稳定性分析模型,并定义为单截面稳定性分析(Single-section stability analysis,S-SA)模型,单截面交通流运行示意图如图2所示 ...

2007

0.0

... 3 双截面稳定性分析模型交通流理论中常采用平均速度差^[15](统计时段内单车道车流中连续通过截面的相邻车辆速度差绝对值的均值)对交通流的离散性进行描述,其主要依靠单截面检测数据对交通流的运行特性进行分析,偏向于反映车辆时间序列上的交通流分布情况,导致对交通流运行特性的分析比较单一、研究范围受限,并且无法在空间位置上对交通流运行的差异进行分析 ...

1998

1.394

0.0

Probab Theory Relat Fields. 1998, 110(3):397-426

A central limit theorem for stationary random fields

Jérôme Dedecker (A1)

A1.URA n° 0743 CNRS, Université de Paris-Sud, Bât. 425, Mathématique, F-91405Orsay Cedex, Francee-mail:Jerome.Dedecker@matups.matups.fr, FR

We prove a central limit theorem for strictly stationary random fields under a projective assumption. Our criterion is similar to projective criteria for stationary sequences derived from Gordin's theorem about approximating martingales. However our approach is completely different, for we establish our result by adapting Lindeberg's method. The criterion that it provides is weaker than martingale-type conditions, and moreover we obtain as a straightforward consequence, central limit theorems for α-mixing or φ-mixing random fields.

2007

0.0

2006

2.006

0.0

. 2006, 14(3):null-null

Evaluation of variable speed limits to improve traffic safety

... 5%),但相关研究表明^[18],汽车尾气中含有CO、CO₂及有害颗粒等对人体及环境的危害极大 ...