考虑侧向偏移的车辆跟驰行为建模及仿真

引用本文

徐程, 曲昭伟, 金盛. 考虑侧向偏移的车辆跟驰行为建模及仿真. 44(6): 1609-1615
XU Cheng, QU Zhao-wei, JIN Sheng. Modeling and simulation of car following behavior considering lateral separation. Journal of Jilin University Engineering and Technology Edition, 44(6): 1609-1615 复制到剪切板

Permissions

考虑侧向偏移的车辆跟驰行为建模及仿真

徐程^1,², 曲昭伟², 金盛³

1.浙江警察学院治安系, 杭州 310053

2.吉林大学交通学院, 长春 130022

3.浙江大学建筑工程学院, 杭州 310058

通信作者:金盛(1982-),男,讲师,博士.研究方向:交通流理论,交通控制.E-mail:jinsheng@zju.edu.cn

作者简介:徐程(1985-),女,硕士.研究方向:交通管理,智能交通.E-mail:grazia_xu@126.com

基金:国家自然科学基金项目(51278220,51208462,51278454); 中央高校基本科研业务费专项基金项目;

摘要

为了描述真实交通环境中车辆交错跟驰的现象,在全速度差模型的基础上引入了视觉角和侧向偏移角的概念,采用侧向偏移角变化率作为衡量车辆横向运动的关键参数并建立了考虑侧向偏移的车辆跟驰模型。通过线性稳定性分析得到了新模型的稳定性条件。理论分析和数值仿真结果表明:改进模型能够有效地描述车辆交错跟驰行为对交通流稳定性的影响,侧向偏移会减少交通流稳定区间,更容易使稳定车流变成时走时停交通流。

关键词: 交通运输系统工程; 跟驰模型; 视觉角; 侧向偏移

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2014)06-1609-07

Modeling and simulation of car following behavior considering lateral separation

XU Cheng^1,², QU Zhao-wei², JIN Sheng³

1.Department of Public Order, Zhejiang Police College, Hangzhou 310053, China

2.College of Transportation, Jilin University, Changchun 130022, China

3.College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

Abstract

In order to describe staggered car following behavior in real traffic environment, a novel car following model was proposed based on Full Velocity Difference (FVD) model by incorporating the visual angle. The rate of change of the lateral separation angle is taken as a key parameter to describe the effect of lateral separation distance. The stability condition of the model was obtained using the linear stability theory. Then the characteristic of the model was investigated by theoretical analysis and numerical simulation. Results show that the lateral separation leads the stability of the proposed model smaller and the easy formation of stop and go traffic. The above findings have great practical significance to improve the stability of traffic flow and analyze car-following characteristics considering the lateral movement.

Keyword: engineering of communications and transportation system; car following model; visual angle; lateral separation

Show Figures

0 引言

车辆跟驰模型是描述在限制超车的单车道上,行驶车队中由于前导车运动状态的变化而引起跟驰车相应反应的模型。20世纪50年代初,Pipes首先开展了对车辆跟驰理论的研究^{[ 1]}。经过60多年的发展,跟驰理论的研究取得了许多富有重要意义的成果^{[ 2, 3]},车辆跟驰理论已成为现代交通流理论的重要组成部分,在交通仿真、智能车辆、交通安全等诸多领域^{[ 4, 5, 6]}都有广泛的应用。

Bando等^{[ 7]}于1995年提出了著名的优化速度(OV)模型,通过微观车辆动力学模型来反应交通流的各种宏观非线性现象。国内外相关学者围绕优化速度模型进行了一系列扩展性的基础研究工作。

Helbing等^{[ 8]}考虑了跟驰车与前导车之间的负速度差效应,建立了广义力(GF)模型。Jiang等^{[ 9]}在GF模型的基础上同时考虑了正速度差的影响,建立了全速度差(FVD)模型。随着智能交通系统的逐渐普及应用,许多学者从理论层面研究多种信息综合作用下的车辆跟驰模型,并探讨了多车跟驰行为对交通流稳定性的影响。Nagatani^{[ 10]}考虑了次邻近前导车对交通流稳定性的影响。Ge等^{[ 11]}提出了双速度差跟驰模型,将前方两辆车的速度差作为调节变量,理论推导并仿真验证了其对改进交通流稳定性具有重要作用。金盛等^{[ 12]}提出了考虑前方交通状态的车辆跟驰行为模型,更加实际地描述了前方多辆车对驾驶行为的影响。

上述研究极大地促进了优化速度模型的发展。这些模型一般都假设车辆在跟驰状态下处于车道中心线位置,即车辆跟驰行为是基于车道的(Lane-based)。然而,由于实际交通环境的复杂性,车辆不可能完全处于车道中心线行驶。特别是在发展中国家,由于道路标志标线不清晰、驾驶行为不规范、道路条件不佳等原因,车辆交错跟驰的现象广泛存在^{[ 13, 14]}。车辆交错跟驰是指跟驰车辆并非完全处于车道中心线位置,跟驰车与前导车之间存在一定的侧向偏移距离,一般称这种现象为非基于车道的(non-lane-based)跟驰行为。这种交错跟驰行为并不能采用传统的优化速度模型进行描述。Tang等^{[ 15]}首先考虑了相邻车道车辆对跟驰行为的影响,进而提出了双车道车辆跟驰模型并进行了交通流稳定性条件分析,结果表明,考虑相邻车道车辆的影响能够有效地增强交通流的稳定性。宋现敏等^{[ 16]}基于人工势能场理论,建立了考虑侧向偏移的车辆跟驰模型并进行了仿真验证。然而,Tang等^{[ 15]}仅考虑了相邻车道前导车与跟驰车之间距离对跟驰行为的影响,而未考虑两辆车之间的运行速度、方位、侧向偏移距离等因素,而这些因素正是影响跟驰车行为的关键因素。

基于此,本文通过对车辆交错跟驰行为特性进行分析,借鉴心理学中驾驶员对信息感知的相关研究成果,以车辆之间的侧偏角变化率作为驾驶员判断车辆横向运动的重要依据,提出了考虑侧向偏移的车辆跟驰行为模型,并对模型进行理论分析和数值仿真,进一步验证了模型的有效性。

1 模型建立

心理学的相关理论和试验研究结论都表明:驾驶员在实际驾驶环境中并不能精确地估计距离、速度、加速度等参数,而是通过前导车在驾驶员眼中的收缩和扩展来判断跟驰车是远离还是接近前导车^{[ 17]}。基于这样的假设,Jin等^{[ 18]}提出了视觉角车辆跟驰模型(VAM),通过在FVD模型中引入视觉角变量,改进了原有模型,使之更加符合实际情况。图1为考虑侧向偏移情况下的车辆跟驰行为示意图。从图中可以看出,前导车与跟驰车运动方向中心线之间存在着一个侧向偏移距离 b,从而导致了两车之间存在一个偏移角 φ。因此,可以采用侧向偏移角及其变化率来表征跟驰车与前导车之间侧向偏移的变化情况,而这种侧向偏移距离的变化会对跟驰车的运动行为产生影响。

	Figure Option View Download New Window
	图1 考虑侧向偏移的车辆跟驰行为示意图Fig.1 Diagram of car following behavior considering lateral separation

通过上述分析可知,采用视觉角和偏移角变量可以有效地描述两车之间纵向和横向运行的关系,因此,将视觉角 θ和偏移角 φ引入到FVD模型中,建立了考虑侧向偏移的车辆跟驰模型,其公式如下:

$\begin{matrix} \begin{matrix} a_{n} (t) = \\ α \{V [θ_{n} (t)] - v_{n} (t)\} - λ_{1} \frac{d}{dt} θ_{n} (t) + λ_{2} \frac{d}{dt} φ_{n} (t) (1) \end{matrix} \end{matrix}$

式中: θ_n( t)为 t时刻第 n辆车驾驶员观察前导车的视觉角; φ_n( t)为 t时刻第 n辆车与其前导车之间的侧向偏移角; V(·)为基于视觉角的优化速度函数; v_n( t)为 t时刻第 n辆车的速度; α为优化速度与当前速度差异的敏感系数; λ₁和 λ₂分别为视觉角 θ与偏移角 φ变化率的敏感系数。其中,视觉角和偏移角为:

$\begin{matrix} \begin{matrix} θ_{n} (t) = \frac{w_{n - 1}}{Δ x_{n} (t) - l_{n - 1}} (2) \\ φ_{n} (t) = \frac{b_{n}}{Δ x_{n} (t) - l_{n - 1}} (3) \end{matrix} \end{matrix}$

式中: Δx_n( t)为 t时刻第 n辆车与前导车之间的车头间距; w_n-₁、 l_n-₁分别为第 n-1辆车的车身宽度和车身长度; b_n为两车之间的侧向偏移距离。

为了能够与FVD模型等其他类似的优化速度模型进行对比分析,在本文的模型中,优化速度函数可以采用1998年Helbing和Tilch^{[ 8]}提出并标定的优化速度函数形式:

$\begin{matrix} V [θ_{n} (t)] = V_{1} + V_{2} \tanh \{C_{1} [w_{n - 1} / θ_{n} (t)] - C_{2}\} (4) \end{matrix}$

式中:相关参数标定结果分别为 V₁=6.75 m/s, V₂=7.91 m/s, C₁=0.13 m^-1, C₂=1.57。

从式(1)可以看出,模型包括两项视觉角变化率的影响项。 -λ₁d θ_n( t) /d t为视觉角变化率对跟驰车辆加速度的影响项。当跟驰车辆远离前导车时,视觉角变化率为负值,因此,视觉角变化率项为正值,车辆会加速前进;反之,视觉角变化率项为负值,跟驰车辆需要减速以避免碰撞。 λ₂d φ_n( t) /d t为侧向偏移角变化率对跟驰车辆加速度的影响项。当前导车逐渐远离跟驰车所在车道中心线,即侧向偏移距离增加时,侧偏角就会随之变大,此时跟驰车就可以进一步加速运行;反之,当前导车逐渐靠近跟驰车所在车道中心线,即侧向偏移距离减少时,侧偏角就会变小,这时跟驰车就需要减速以避免碰撞。当 λ₂=0时,即不考虑侧向偏移效应,模型就简化为视觉角模型^{[ 18]}。上述两项分别定量描述了跟驰车与前导车之间的纵向视觉角和侧向偏移角变化对跟驰车加速度的影响。

2 线性稳定性分析

假设初始状态为稳定态,则所有车辆均以固定的车头间距 h运行。其对应的稳态优化速度为 V( θ₀),同时视觉角变化率为零,则任意车辆的位置可以表示为:

$\begin{matrix} x_{n}^{0} (t) = hn + V (θ_{0}) t (5) \end{matrix}$

式中: θ₀为稳态下的视觉角, θ₀ =w_n-₁ /( h-l_n-₁)。

定义 y_n( t)为对车辆所施加的微小扰动,则:

$\begin{matrix} x_{n} (t) = x_{n}^{0} (t) + y_{n} (t) (6) \end{matrix}$

引入微小扰动后,重新改写式(2)可以得到:

$\begin{matrix} \begin{matrix} θ_{n} (t) = \frac{w_{n - 1}}{h + Δ y_{n} (t) - l_{n - 1}} = \\ \frac{w_{n - 1} [(h - l_{n - 1}) - Δ y_{n} (t)]}{(h - l_{n - 1})^{2} - {[Δ y_{n} (t)]}^{2}} (7 a) \end{matrix} \end{matrix}$

将式(7a)中 Δy_n( t)的高阶项去掉,并对时间进行求导,可以得到视觉角及视觉角变化率的最终表达式为:

$\begin{matrix} \begin{matrix} θ_{n} (t) = \frac{w_{n - 1}}{(h - l_{n - 1})} - \frac{w_{n - 1}}{(h - l_{n - 1})^{2}} Δ y_{n} (t) \\ (7 b) \\ \frac{d}{dt} θ_{n} (t) = - \frac{w_{n - 1}}{(h - l_{n - 1})^{2}} Δy'_{n} (t) (8) \end{matrix} \end{matrix}$

类似地,将式(3)重新进行改写并对时间进行求导,可以得到:

$\begin{matrix} \begin{matrix} φ_{n} (t) = \frac{b_{n}}{h + Δ y_{n} (t) - l_{n - 1}} = \\ \frac{b_{n} [(h - l_{n - 1}) - Δ y_{n} (t)]}{(h - l_{n - 1})^{2} - {[Δ y_{n} (t)]}^{2}} (9 a) \\ φ_{n} (t) = \frac{b_{n}}{(h - l_{n - 1})} - \frac{b_{n}}{(h - l_{n - 1})^{2}} Δ y_{n} (t) (9 b) \\ \frac{d}{dt} φ_{n} (t) = - \frac{b_{n}}{(h - l_{n - 1})^{2}} Δy'_{n} (t) (10) \end{matrix} \end{matrix}$

将式(7b)(8)(10)代入模型,并进行线性化可以得到:

$\begin{matrix} \begin{matrix} y ″_{n} (t) = \\ α \{V' (θ_{0}) [- \frac{w_{n - 1}}{{(h - l_{n - 1})}^{2}} Δ y_{n} (t)] - y'_{n} (t)\} + \\ \frac{λ_{1} w_{n - 1} - λ_{2} b_{n}}{{(h - l_{n - 1})}^{2}} Δy'_{n} (t) (11) \\ V' (θ_{0}) = {\frac{dV (θ)}{dθ}|}_{θ = θ_{0}} (12) \end{matrix} \end{matrix}$

将式(11)中的 y_n( t)以傅立叶模式展开为 y_n( t) =Aexp( ikn+zt),这样就可以得到如下公式:

$\begin{matrix} \begin{matrix} z^{2} = α [- V' (θ_{0}) \frac{w_{n - 1}}{(h - l_{n - 1})^{2}} (e^{ik} - 1) - z] + \\ \frac{λ_{1} w_{n - 1} - λ_{2} b_{n}}{{(h - l_{n - 1})}^{2}} z (e^{ik} - 1) (13) \end{matrix} \end{matrix}$

将 z展开为 z=z₁( ik) +z₂( ik)² +…形式,并带入式(13),舍去高阶项,则 z的一阶和二阶项系数分别为:

$\begin{matrix} \{\begin{matrix} z_{1} = - \frac{w_{n - 1}}{{(h - l_{n - 1})}^{2}} V' (θ_{0}); \\ z_{2} = - \frac{V' (θ_{0}) w_{n - 1}}{α {(h - l_{n - 1})}^{2}} \{\frac{α}{2} + \\ \frac{w_{n - 1} [V' (θ_{0}) + λ_{1}] - λ_{2} b_{n}}{{(h - l_{n - 1})}^{2}}\} \end{matrix} (14) \end{matrix}$

当 z₂ =0时,即得到临界稳定条件:

$\begin{matrix} V' (θ_{0}) = - \frac{α {(h - l_{n - 1})}^{2}}{2 w_{n - 1}} - (λ_{1} - λ_{2} \frac{b_{n}}{w_{n - 1}}) (15) \end{matrix}$

当 λ₂ =0或 b_n=0时,稳定性条件被简化,与文献[18]中的稳定性条件一致,这也证明了视觉角模型是该模型的一个特殊形式。

图2(a)给出了在 λ₁ =20, λ₂ =10时,不同 b值下的临界稳定曲线示意图。在临界曲线下方,交通流是非稳定的,即均匀车流最终会发展成拥挤车流。随着侧向偏移距离 b的增加,临界曲线变得越来越高,即稳定区间变小。这表明,随着车辆侧向偏移距离的增加,车辆之间的侧偏角变化率也会随之增加,这样就加剧了车流的不稳定性。从图2(a)中可以明显看出,临界稳定性曲线呈现不对称特性,造成这一特性的主要原因是:在较大车头间距下,驾驶员对视觉角的变化率较为不敏感,车辆的微小运动不易被驾驶员所察觉,当这些微小的变化积累到一定程度后,驾驶员才做出较大的反应,从而导致稳定性区间变小;而在较小的车头间距下,驾驶员对视觉角的微小变化都会立即做出相应的反应,因而稳定性区间较大,车流更易于稳定。同理,由于驾驶员对视觉角变化率的敏感程度随着车头间距的增加而减小,随着侧向偏移距离的增加,不稳定性区域在小车头间距下要比大车头间距下增加得更快。

图2(b)给出了在 λ₁ =20, b=1 .0时,不同 λ₂值下的临界稳定曲线示意图。从图中可以看出,其具有与图2(a)类似的性质,随着 λ₂的增加,交通流的稳定性区间减小。该图所表现出来的交通流在畅通和拥挤状态下的非对称特性能够更加真实地反映驾驶员的真实驾驶行为。

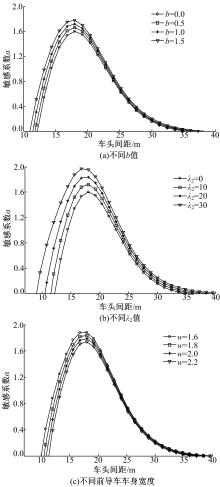	Figure Option View Download New Window
	图2 不同 b值、 λ₂值和前导车车身宽度下的车头间距与敏感系数 α之间的临界曲线Fig.2 Critical curves between headway and sensitivity α under different parameter values b, λ₂ and front vehicle lengths

根据式(1)可知,前导车的车身宽度会直接影响视觉角及侧偏角的大小,进而会对跟驰车的动力学特性产生重要影响。为了验证车身宽度对交通流稳定性特性的影响, 图2(c)给出了车身宽度从1.6 m变化到2.2 m情况下的临界稳定曲线。从图中可以看出,随着前导车车身宽度的增加,交通流临界稳定性曲线明显下降,交通流的稳定性区间增大。产生这一现象的主要原因是:在相同的距离变化情况下,随着前导车车身宽度的增大,驾驶员感知到的前导车侧偏角变化率也会随之增大。也就是说,驾驶员对大车的刺激更加敏感,因而能够更快地做出相应的反应。这一结论与实际驾驶行为是一致的,即驾驶员在跟驰大车时,会给予更多的关注以避免发生危险。上述结论为分析车辆类型对交通流稳定性的影响提供了一种新思路。

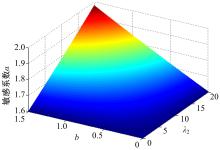
为了进一步分析参数 b和 λ₂与交通流临界稳定曲线的关系, 图3给出了不同参数组合下的临界曲线顶点变化图。从图中可以看出:随着参数值的增大,稳定性曲线临界点也随之增大,这表明随着侧向偏移距离及敏感系数的增大,交通流的非稳定性区间逐渐增大,导致交通流严重失稳,均匀交通流逐渐演化为时走时停交通流。上述结论与实际经验中车辆换道行为会对交通流稳定性产生影响以及文献[15-16]中的结论类似。

	Figure Option View Download New Window
	图3 不同 λ₂值和 b值组合下临界点三维图Fig.3 Three-dimensional map of the critical point under different parameter values λ₂ and b

3 数值仿真及分析

为了进一步分析所建立模型的相关动力学特性以及验证理论分析的正确性,下面将对跟驰模型进行数值仿真,以此来验证仿真结果与理论分析的一致性。在跟驰模型仿真中采用如下的更新规则:

$\begin{matrix} \{\begin{matrix} v_{n} (t + Δt) = v_{n} (t) + Δt \cdot a_{n} (t) \\ x_{n} (t + Δt) = x_{n} (t) + Δt \cdot [v_{n} (t) + \\ v_{n} (t + Δt)] / 2 \end{matrix} (16) \end{matrix}$

在仿真中采用周期边界条件,环路长度 L=1500 m,车辆数 N=100,敏感系数 α=0.41,仿真时间间隔Δ t=0.1 s。此外,模型中采用固定的车身宽度及车身长度值,即 w₀=1.8 m, l₀=5 m。同时,前后两车之间的侧向偏移距离也认为是相同的。仿真初始条件为:

$\begin{matrix} \{\begin{matrix} x_{1} (0) = 1 m \\ x_{n} (0) = (n - 1) L / Nforn \neq 1 \\ v_{n} (0) = V [w_{0} / (L / N - l_{0})] \end{matrix} (17) \end{matrix}$

	Figure Option View Download New Window
	图4 不同参数组合下的车辆时空图Fig.4 Space-time diagram under different model parameters

图4给出了在 λ₁=40、 λ₂=20时,前后两车之间的侧向偏移距离 b分别为0、0.5、1.0和1.5 m时,在经过较长时间运行后,从2000 s到2100 s之间的车辆车头间距时空分布图。根据临界稳定性条件可知,在 b=0时,如图4(a)中交通流处于稳定区间内,模型就简化为视觉角模型^{[ 18]},这时始终能够维持车辆均匀,微小扰动传播并不会扩大。随着车辆之间侧向偏移距离 b的增大, 图4(b)(c)(d)中密度波的振幅也逐渐增大,均匀交通流逐渐发展成为时走时停交通流。这时交通流存在明显的分界,一部分车流处于拥挤状态,速度很低,密度很大;另一部分车流处于自由行驶状态,速度较快。这与线性稳定性理论分析的结果是一致的,表明随着侧向偏移距离的增大,将会导致交通流不稳定性加剧。因此,本文提出的模型不仅能够描述车辆纵向运动之间的关系,同时能够表达前后车辆之间横向位置变化对交通流稳定性的影响。

	Figure Option View Download New Window
	图5 不同参数下车辆速度分布图Fig.5 Distribution of vehicle speeds under different model parameters

图5给出了侧偏角变化率敏感参数 λ₂取不同值时,车辆在仿真300 s及2000 s后的速度分布图,其中 λ₁=40、 b=1.0 m。随着 λ₂值的增加,车辆速度分布呈现越来越明显的波动特性,交通流时走时停现象加剧。同时,从速度分布图中可以看出明显的加减速非对称特性,这与其他研究中的结论是一致的^{[ 18, 19]}。随着 λ₂值的增加,这种非对称性越发明显,车辆从低速加速到最大速度所经历的时间要远远大于从最大速度减速到低速的时间。造成这一现象的本质原因是由于视觉角及侧偏角在加速和减速过程中其变化率是不对称的。当车辆较为接近时,由于车头间距较小,相同的距离变化导致视觉角变化率远大于较大车头间距下的情况。因此,引入视觉角及侧偏角作为影响驾驶员行为的关键变量能够更加真实地反应驾驶中人的行为特性。

4 结论

(1)采用视觉角和侧偏角指标比单纯的速度、距离指标能够更好地反映前导车对跟驰车的影响,通过视觉角及其变化率可以反映前导车速度、距离的综合变化,而侧偏角变化率可以反映前导车相对于跟驰车横向位置的变化。

(2)引入侧向偏移参数后,能够表达车辆之间横向位置变化对交通流稳定性的影响。理论分析和仿真测试结果都表明,侧向偏移距离会导致交通流失稳。这进一步说明了相邻车道车辆、路边停车、路边障碍物等因素都会对交通流稳定性产生影响,这一结论与实际情况是一致的。

(3)视觉角和侧偏角变量的引入能够表现出车辆加减速的非对称特性,也更加符合真实交通环境中驾驶员对前导车运行状况所作出的行为反应特性。

(4)通过模型分析可知,车辆宽度会对交通流稳定性产生影响,随着前导车宽度的增大,跟驰车对其产生的刺激也具有更大的敏感性,因而对交通流具有致稳作用。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Pipes L A. An operational analysis of traffic dynamics[J]. Journal of Applied Physics, 1953, 24(3): 274-281. [本文引用:1] [JCR: 2.21]
[2]	Brackstone M, Mcdonald M. Car-following: a historical review[J]. Transportation Research Part F, 1999, 2(4): 181-196. [本文引用:1]
[3]	Chowdhury D, Santen L, Schadschneider A. Statistical physics of vehicular traffic and some related systems[J]. Physical Report, 2000, 329(4): 199-329. [本文引用:1]
[4]	Meng Q, Qu X. Estimation of rear-end vehicle crash frequencies in urban road tunnels[J]. Accident Analysis and Prevention, 2012, 48(1): 254-263. [本文引用:1]
[5]	Qu X, Meng Q, Yuanita V, et al. Design and implementation of a quantitative risk assessment software tool for singapore's road tunnels[J]. Expert Systems with Applications, 2011, 38(11): 13827-13834. [本文引用:1] [JCR: 1.854]
[6]	Meng Q, Qu X, Yong K T, et al. QRA model-based risk impact analysis of traffic flow in urban road tunnels[J]. Risk Analysis, 2011, 31(12): 1872-1882. [本文引用:1] [JCR: 2.278]
[7]	Band o M, Hasebe K, Nakayama A, et al. Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51(2): 1035-1042. [本文引用:1] [JCR: 2.313]
[8]	Helbing D, Tilch B. Generalized force model of traffic dynamics[J]. Physical Review E, 1998, 58(1): 133-138. [本文引用:2] [JCR: 2.313]
[9]	Jiang R, Wu Q S, Zhu Z J. Full velocity difference model for a car-following theory[J]. Physical Review E, 2001, 64(1): 7101-7104. [本文引用:1] [JCR: 2.313]
[10]	Nagatani T. Stabilization and enhancement of traffic flow by the next-nearest-neighbor interaction[J]. Physical Review E, 1999, 60(6): 6395-6401. [本文引用:1] [JCR: 2.313]
[11]	Ge H X, Cheng R J, Li Z P. Two velocity difference model for a car following theory[J]. Physica A, 2008, 387(21): 5239-5245. [本文引用:1] [JCR: 1.676]
[12]	金盛, 王殿海. 考虑前方交通状态的车辆跟驰模型与数值仿真[J]. 北京工业大学学报, 2012, 38(8): 1236-1241. Jin Sheng, Wang Dian-hai. Car following model and simulation considering front traffic situation[J]. Journal of Beijing Polytechnic University, 2012, 38(8): 1236-1241. [本文引用:1]
[13]	Gunay B. Car following theory with lateral discomfort[J]. Transportation Research Part B, 2007, 41(7): 722-735. [本文引用:1] [JCR: 2.944]
[14]	Jin S, Wang D H, Tao P F, et al. Non-lane-based full velocity difference car following model[J]. Physica A, 2010, 389(21): 4654-4662. [本文引用:1] [JCR: 1.676]
[15]	Tang T Q, Huang H J, Gao Z Y. Stability of the car-following model on two lanes[J]. Physical Review E, 2005, 72(6): 6142-6148. 宋现敏, 金盛, 王殿海, 等. 考虑侧向偏移的车辆跟驰模型[J]. 吉林大学学报: 工学版, 2011, 41(2): 333-337. Song Xian-min, Jin Sheng, Wang Dian-hai, et al. Vehicle-following model considering lateral offset[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(2): 333-337. [本文引用:]
	[本文引用:2] [JCR: 2.313]
[17]	Andersen G J, Sauer C W. Optical information for car following: the driving by visual angle(DVA) model[J]. Human Factors, 2007, 49(5): 878-896. [本文引用:1]
[18]	Jin S, Wang D H, Huang Z Y, et al. Visual angle model for car following theory[J]. Physica A, 2011, 390(11): 1931-1940. [本文引用:3] [JCR: 1.676]
[19]	Gong H X, Liu H C, Wang B H. An asymmetric full velocity difference car-following model[J]. Physica A, 2008, 387(11): 2595-2602. [本文引用:1] [JCR: 1.676]

1953

2.21

0.0

... 20世纪50年代初,Pipes首先开展了对车辆跟驰理论的研究^[1] ...

1999

0.0

. 1999, 2(4):null-null

Car-following: a historical review

2000

0.0

. 2000, 329(4):null-null

Statistical physics of vehicular traffic and some related systems

2012

0.0

. 2012, 48(1):null-null

Estimation of rear-end vehicle crash frequencies in urban road tunnels

2011

1.854

0.0

. 2011, 38(11):13827-13834 DOI:10.1016/j.eswa.2011.04.186

Design and implementation of a quantitative risk assessment software tool for singapore's road tunnels

Abstract

This paper presents an interesting approach to develop a quantitative risk assessment (QRA) software tool for road tunnels. It first introduces a QRA model for road tunnels, consisting of event trees, fault trees and consequence estimation models. The model is developed by taking into account the unique characteristics of Singapore road tunnels. The paper proceeds to describe design of the QRA software tool based on the QRA model by means of the object oriented design (OOD) method and eXtensible Markup Language (XML) technique. The XML files are used to store the numerous tree structures in the proposed model thus making the programming much more efficiently and effectively. The QRA software tool is robust and flexible such that users can easily add or modify the event trees, fault trees and the consequence estimation models. An application to Singapore road tunnels has been carried out to assess the robustness and effectiveness of the QRA software tool.

Highlights

? A risk assessment software tool for road tunnels. ? Tree structures are represented by XML files. ? Object oriented software design.

2011

2.278

0.0

. 2011, 31(12):1872-1882

QRA Model-Based Risk Impact Analysis of Traffic Flow in Urban Road Tunnels

Qiang Meng †,* ,Xiaobo Qu † ,Kum Thong Yong ‡ andYoke Heng Wong ‡

<sup>*</sup> Assoc Prof. Qiang Meng, Department of Civil and Enviornment Engineering, National University of Singapore, 10 Kent Ridge Crescent, Singapore 117576; tel: +65-65165494; fax: +65-67791635; <a href="mailto:cvemq@nus.edu.sg" title="Link to email address" shape="rect">cvemq@nus.edu.sg</a>.

Road tunnels are vital infrastructures providing underground vehicular passageways for commuters and motorists. Various quantitative risk assessment (QRA) models have recently been developed and employed to evaluate the safety levels of road tunnels in terms of societal risk (as measured by the F/N curve). For a particular road tunnel, traffic volume and proportion of heavy goods vehicles (HGVs) are two adjustable parameters that may significantly affect the societal risk, and are thus very useful in implementing risk reduction solutions. To evaluate the impact the two contributing factors have on the risk, this article first presents an approach that employs a QRA model to generate societal risk for a series of possible combinations of the two factors. Some combinations may result in F/N curves that do not fulfill a predetermined safety target. This article thus proposes an “excess risk index” in order to quantify the road tunnel risk magnitudes that do not pass the safety target. The two-factor impact analysis can be illustrated by a contour chart based on the excess risk. Finally, the methodology has been applied to Singapore's KPE road tunnel and the results show that in terms of meeting the test safety target for societal risk, the traffic capacity of the tunnel should be no more than 1,200 vehs/h/lane, with a maximum proportion of 18% HGVs.

1995

2.313

0.0

. 1995, 51(2):chrome=1" http-equiv="X-UA-Compatible" /><title>Phys. Rev. E 51, 1035-null

... Bando等^[7]于1995年提出了著名的优化速度(OV)模型,通过微观车辆动力学模型来反应交通流的各种宏观非线性现象 ...

1998

2.313

0.0

. 1998, 58(1):chrome=1" http-equiv="X-UA-Compatible" /><title>Phys. Rev. E 58, 133-null

... Helbing等^[8]考虑了跟驰车与前导车之间的负速度差效应,建立了广义力(GF)模型 ...

... 为了能够与FVD模型等其他类似的优化速度模型进行对比分析,在本文的模型中,优化速度函数可以采用1998年Helbing和Tilch^[8]提出并标定的优化速度函数形式: ...

2001

2.313

0.0

... Jiang等^[9]在GF模型的基础上同时考虑了正速度差的影响,建立了全速度差(FVD)模型 ...

1999

2.313

0.0

. 1999, 60(6):chrome=1" http-equiv="X-UA-Compatible" /><title>Phys. Rev. E 60, 6395-null

... Nagatani^[10]考虑了次邻近前导车对交通流稳定性的影响 ...

2008

1.676

0.0

. 2008, 387(21):null-null

Two velocity difference model for a car following theory

... Ge等^[11]提出了双速度差跟驰模型,将前方两辆车的速度差作为调节变量,理论推导并仿真验证了其对改进交通流稳定性具有重要作用 ...

2012

0.0

... 金盛等^[12]提出了考虑前方交通状态的车辆跟驰行为模型,更加实际地描述了前方多辆车对驾驶行为的影响 ...

2007

2.944

0.0

. 2007, 41(7):722-735 DOI:10.1016/j.trb.2007.02.002

Car following theory with lateral discomfort

Abstract

A car following model has been developed with particular reference to weak discipline of lane-based driving. The theory is based on the discomfort caused by lateral friction between vehicles. The movement of the following vehicle was formulated as a function of the off-centre effects of its leader(s). This incorporation of lateral friction offers a potential breakthrough in the fields of car following theory and microscopic simulation of traffic flow. Using a stopping-distance car following approach, the simulation presented in the paper pointed out the effect of the travel path width on the speed of the following vehicle, and the reduced following distance with increased lateral separation between the leader and follower. It was also shown that a special case of the proposed model (i.e. when the maximum escape speed is zero) produced the same results as the base model did for the conventional car following case. The simulation behaved rationally giving credibility to the author’s staggered car following theory.

2010

1.676

0.0

. 2010, 389(21):null-null

Non-lane-based full velocity difference car following model

2005

2.313

0.0

... Tang等^[15]首先考虑了相邻车道车辆对跟驰行为的影响,进而提出了双车道车辆跟驰模型并进行了交通流稳定性条件分析,结果表明,考虑相邻车道车辆的影响能够有效地增强交通流的稳定性 ...

... 然而,Tang等^[15]仅考虑了相邻车道前导车与跟驰车之间距离对跟驰行为的影响,而未考虑两辆车之间的运行速度、方位、侧向偏移距离等因素,而这些因素正是影响跟驰车行为的关键因素 ...

2007

0.0

... 1 模型建立心理学的相关理论和试验研究结论都表明:驾驶员在实际驾驶环境中并不能精确地估计距离、速度、加速度等参数,而是通过前导车在驾驶员眼中的收缩和扩展来判断跟驰车是远离还是接近前导车^[17] ...

2011

1.676

0.0

. 2011, 390(11):null-null

Visual angle model for car following theory

... 基于这样的假设,Jin等^[18]提出了视觉角车辆跟驰模型(VAM),通过在FVD模型中引入视觉角变量,改进了原有模型,使之更加符合实际情况 ...

... ₂=0时,即不考虑侧向偏移效应,模型就简化为视觉角模型^[18] ...

... 根据临界稳定性条件可知,在b=0时,如图4(a)中交通流处于稳定区间内,模型就简化为视觉角模型^[18],这时始终能够维持车辆均匀,微小扰动传播并不会扩大 ...

2008

1.676

0.0

. 2008, 387(11):null-null

An asymmetric full velocity difference car-following model