随机交通网络环境下自适应最可靠路径问题

引用本文

潘义勇, 孙璐. 随机交通网络环境下自适应最可靠路径问题. 44(6): 1622-1627
PAN Yi-yong, SUN Lu. Adaptive reliable shortest path problem in stochastic traffic network. Journal of Jilin University Engineering and Technology Edition, 44(6): 1622-1627 复制到剪切板

Permissions

随机交通网络环境下自适应最可靠路径问题

潘义勇^1,², 孙璐^2,³

1.南京林业大学汽车与交通工程学院

2.东南大学交通学院,南京 210096

3.美国Catholic大学土木工程系,美国华盛顿特区 200064

通信作者:孙璐(1972-),男,教授,博士生导师.研究方向:交通工程,道路工程.E-mail:sunl@cua.edu.cn

作者简介:潘义勇(1980-),男,博士研究生.研究方向:交通网络最优路径.E-mail:uoupanyg@gmail.com

基金:国家自然科学基金重点项目(U1134206); 国家自然科学基金外青学者项目(51250110075, 51050110143); 交通运输部西部项目(0901005C); 江苏省自然科学基金创新学者攀登计划项目(SBK200910046); 美国国家科学基金总统奖项目(CMMI-0408390); 美国国家科学基金项目(CMMI-0644552);

摘要

为了研究交通网络耗时最优路径选择问题,建立了随机网络环境下自适应最可靠路径问题的数学模型。首先,建立随机网络模型反映交通网络的耗时随机特性;其次,在该网络环境下定义最可靠路径策略和最可靠状态链,并且证明最可靠状态链满足动态规划的 Bellman's准则;第三,构造基于动态规划的逐次逼近算法求解该问题,并且证明提出的逐次逼近算法是多项式时间算法;最后,编写基于MATLAB计算机语言的算法程序,并针对实际交通网络Sioux Falls (SF) network展开数值试验,计算结果验证了该算法的正确性和可行性。

关键词: 智能交通; 随机网络; 可靠性; 动态规划; 最短路

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2014)06-1622-06

Adaptive reliable shortest path problem in stochastic traffic network

PAN Yi-yong^1,², SUN Lu^2,³

1.College of Automobile and Traffic Engineering,Nanjing Forestry University,Nanjing 210037,China

2.School of Transportation, Southeast University, Nanjing 210096, China

3.Department of Civil Engineering, The Catholic University of America, Washington DC 200064, USA

Abstract

In order to analyze the problem of selecting optimal path in traffic network, adaptive reliable shortest path problem is addressed in stochastic network. First, the mathematical model of stochastic traffic network is established to reflect the stochastic characteristic of traffic time in traffic network. Second, the optimal-reliable routing policy and optimal-reliable state chain based on reliability theory are uniformly defined in stochastic network; and the optimal-reliable state chain satisfies Bellman's principle that is the core of dynamic programming. Third, a successive approximation algorithm based on the dynamic programming is developed to solve the adaptive reliable shortest path problem in stochastic network, whose complexity is polynomial time. Finally, a computer program using Matlab language is developed to compute on the Sioux-Falls (SF) network. Numerical results in typical transportation network show the validity and feasibility of the successive approximation algorithm.

Keyword: intelligent transportation; stochastic network; reliability; dynamic programming; shortest path

Show Figures

0 引言

最优路径问题是智能交通系统(Intelligent transportation system,ITS)中路径诱导子系统(Route guidance system,RGS)的核心问题。近年来,交通拥挤、道路阻塞和交通事故的频繁发生正越来越严重地困扰着世界各国的大城市。为了提高运输网络使用效率,解决交通拥挤和交通安全问题,美国、日本和欧盟等发达国家均加大了对智能交通系统的研究。智能交通系统是解决现代社会交通需求与交通供给两者之间矛盾的重要途径之一^{[ 1]}。作为智能交通系统核心子系统之一的路径诱导系统(RGS)是各国竞相角逐的研究热点^{[ 2, 3]},交通网络最优路径问题是路径诱导系统的核心问题之一。

随机网络指网络的边的权值是随机变量。可以描述交通网络行程时间的随机特性。例如,将交通网络中通过某路段的时间耗费看作网络中边的权值,该网络边的权值是不确定的,是一个服从一定概率分布函数的随机变量^{[ 4]}。

随机路径分为两种路径:先验路径和自适应路径,Hall^{[ 3]}在1986年指出自适应路径比先验路径更优,并且给出了小的算例验证了该定理的正确性。2006年Gao and Chabini^{[ 5]}和2012年Gao and Huang^{[ 8]}也对这个结论给出了验证。另外,基于先进旅行者信息系统(ATIS)的车载导航系统(in-vehicle route guidance system)的发展和广泛应用,在线的自适应路径问题越来越受到重视,有必要针对随机网络环境下自适应路径问题展开研究。

在随机交通网络环境下,路径目标策略常常把最小期望值看成是最优策略^{[ 5, 6, 7, 8, 9]},但是最小期望值的路径不能保证方差最小,可能该路径的风险很大,对于风险规避的行驶者是不可取的。大量的实证研究表明行驶者不仅关注行程时间的节省而且关注行程时间的可靠性^{[ 10, 11, 12, 13]}。可靠度作为可靠性理论的重要指标,在工程上已经得到了广泛应用^{[ 14]}。另外一种最优策略是可靠度最大,寻找在给定的预留时间内到达目的地的最大概率的路径。目前,国内外鲜有文献对随机交通网络环境下自适应最可靠路径问题及其求解算法展开讨论,而这正是本研究的目的。首先,建立随机网络模型反映交通网络的耗时随机特性;其次,在此网络环境下基于可靠性理论定义最可靠路径策略和最可靠状态链,并且证明最可靠状态链满足动态规划的Bellman’s准则;第三,构造基于动态规划的逐次逼近算法求解该问题,并且证明该算法是收敛的,且为多项式时间算法;最后,通过MATLAB计算机语言实现了算法程序,并针对实际交通网络:Sioux Falls(SF)network展开数值试验,计算结果验证了该算法的正确性和可行性。

1 问题模型

1.1 随机交通网络

随机网络 G=( N, A, $\begin{matrix} \tilde{X} \end{matrix}$ ), N( $\begin{matrix} |N| \end{matrix}$ =n)是节点的集合, A( $\begin{matrix} |A| \end{matrix}$ =m)是边的集合。每个节点 i都有若干前节点和后节点与之连接,前节点的集合记为 Φ( i) = $\begin{matrix} \{j, (i, j) \in A\} \end{matrix}$ ,后节点的集合记为 Φ^-¹( i) = $\begin{matrix} \{k, (k, i) \in A\} \end{matrix}$ 。边( i, j)的行程时间可以建模为连续型的随机变量 $\begin{matrix} {\tilde{X}}_{ij} \end{matrix}$ 。对于每一个边( i, j), $\begin{matrix} {\tilde{X}}_{ij} \end{matrix}$ 是服从概率分布密度函数 f_ij( x)的连续型随机变量。另外,随机网络中每条边( i, j)的随机变量 $\begin{matrix} {\tilde{X}}_{ij} \end{matrix}$ 是独立的。

1.2 自适应最可靠路径问题

假设行驶者在决策点 i∈ N,根据当前的状态 x_i=( i, b)选择下一个节点,其 i是当前节点, b∈ B是当前的行程时间预算,其中 B是行程时间预算的集合。

定义 N和集合 B的笛卡尔积的集合:

Ω=N×B

自适应路径策略是集合 Ω到集合 N的函数:

μ: Ω→ N

μ( i, b)表示根据当前的状态选择的下一个节点。

假设行驶者根据自适应路径策略 μ: Ω→ N选择的下一个节点是 j,下一个节点的当前状态 x_j= $\begin{matrix} \{j, \tilde{b}\} \end{matrix}$ 是不确定的, $\begin{matrix} \tilde{b} \end{matrix}$ 是随机变量。边( i, j)的行程时间 ij是随机变量,所以下一个节点 j的行程时间预算 $\begin{matrix} \tilde{b} \end{matrix}$ =b-ij也是随机变量。

定义状态链 μ^od={ x_o,…, x_i, x_j,…, x_d}为行驶者根据自适应路径策略 μ: Ω→ N在行程中所经历状态的时间序列,其中 x_o=( o, b)和 x_d=( d, $\begin{matrix} \tilde{b} \end{matrix}$ )分别是起点 o∈ N和终点 d∈ N的状态。旅行者根据自适应路径策略 μ: Ω→ N可能经历不同的状态链。给定起始状态 x_o=( o, b)和自适应路径策略 μ: Ω→ N,起点和终点之间的行程时间为随机变量 $\begin{matrix} {\tilde{S}}_{μ}^{od} \end{matrix}$ 。终点的当前状态 x_d=( d, $\begin{matrix} \tilde{b} \end{matrix}$ )是不确定的,终点的行程时间预算 $\begin{matrix} \tilde{b} \end{matrix}$ =b- $\begin{matrix} {\tilde{S}}_{μ}^{od} \end{matrix}$ 是随机变量。状态链的当前节点构成了一条路径。

设 U_μ( x_o) =P( $\begin{matrix} {\tilde{S}}_{μ}^{od} \end{matrix}$ ≤ b)为事件 $\begin{matrix} {\tilde{S}}_{μ}^{od} \end{matrix}$ ≤ b发生的概率,则自适应最可靠路径问题定义为:

$\begin{matrix} U_{μ}^{*} \end{matrix}$ ( x_o) =max $\begin{matrix} \{P ({\tilde{S}}_{μ}^{od} \leq b), \forall μ\} \end{matrix}$ ,

μ^*( x_o) =argmax $\begin{matrix} \{P ({\tilde{S}}_{μ}^{od} \leq b), \forall μ\} \end{matrix}$

定义1( b-最可靠路径策略).给定行程时间预算 b,路径策略 μ^*是 b-最可靠的策略当且仅当

μ^*( i, b-x) =argmax $\begin{matrix} \{U_{μ} (i, b - x), \forall μ\} \end{matrix}$ ,∀ i∈ N, x∈[0, b)。

定义2( b-最可靠状态链) .依据 b-最可靠路径策略 μ^*所构成的时间序列链{ x_i, x_j,…, x_d}称为 b-最可靠状态链。

定理1 b-最可靠状态链的任意子链都是 b-最可靠状态链。

证明(反证法) 假设{ x_i, x_j,…, x_d}是 b-最可靠状态链,并且它的子链{ x_j,…, x_k}不是 b-最可靠状态链。因此,存在路径策略 μ'使得对某一个 z∈[0, b), P( $\begin{matrix} {\tilde{S}}_{_{μ^{*}}}^{jk} \end{matrix}$ ≤ b-z) <P( $\begin{matrix} {\tilde{S}}_{_{μ'}}^{jk} \end{matrix}$ ≤ b-z)。

$\begin{matrix} {\tilde{S}}_{μ}^{id} \end{matrix}$ 和 $\begin{matrix} {\tilde{S}}_{μ}^{jk} \end{matrix}$ 的关系是:

$\begin{matrix} {\tilde{S}}_{μ}^{id} \end{matrix}$ = $\begin{matrix} {\tilde{X}}_{ij} \end{matrix}$ + $\begin{matrix} {\tilde{S}}_{μ}^{jk} \end{matrix}$ + $\begin{matrix} {\tilde{X}}_{kd} \end{matrix}$

因此: U_μ( i, b) =P $\begin{matrix} ({\tilde{X}}_{ij} + {\tilde{S}}_{μ}^{jk} + {\tilde{X}}_{kd} \leq b) \end{matrix}$ =

$\begin{matrix} \int_{0}^{b} \end{matrix}$ f_ij( x) $\begin{matrix} \int_{0_{}}^{{b-x}_{}} \end{matrix}$ f_kd( y) ×P $\begin{matrix} ({\tilde{S}}_{μ}^{jk} \leq b - x - y) \end{matrix}$ d yd x

因为对某一个 z∈[0, b),

P $\begin{matrix} ({\tilde{S}}_{_{μ^{*}}}^{jk} \leq b - z) \end{matrix}$ <P $\begin{matrix} ({\tilde{S}}_{_{μ'}}^{jk} \leq b - z) \end{matrix}$ ,所以

$\begin{matrix} \begin{matrix} U_{_{μ^{*}}} (i, b) = P ({\tilde{X}}_{ij} + {\tilde{S}}_{_{μ^{*}}}^{jk} + {\tilde{X}}_{kd} \leq b) = \\ \int_{0}^{b} f_{ij} (x) \int_{0_{}}^{{b-x}_{}} f_{kd} (y) \times P ({\tilde{S}}_{_{μ^{*}}}^{jk} \leq \\ b - x - y) dydx < \\ \int_{0}^{b} f_{ij} (x) \int_{0_{}}^{{b-x}_{}} f_{kd} (y) \times P ({\tilde{S}}_{_{μ'}}^{jk} \leq \\ b - x - y) dydx = U'_{μ} (i, b) \end{matrix} \end{matrix}$

这与假设{ x_i, x_j,…, x_d}是 b-最可靠状态链相矛盾。

定理2在随机网络环境下, b-最可靠状态链不包含回路。

证明(反证法) 假设状态链 μ^id={ x_i,…, x_d}和 l^id={ x_i,…, x_i,…, x_d}都是 b-最可靠状态链,其中状态链 l^id={ x_i,…, x_i,…, x_d}包含了起点和终点都是节点 i的回路。注意任何的回路都可以看成是一个子路径,因此得:

U_l( i, b-y) =

$\begin{matrix} \int_{0_{}}^{{b-y}_{}} \end{matrix}$ f_i-i( x) ×U_μ( i, b-y-x)d x,∀ y∈[0, b]

其中 f_i-i( x)是回路 i-i随机行程时间的概率密度函数。因为:

U_μ( i, b-x-y)≤ U_μ( i, b-y)

其中不等式成立是因为累积概率分布函数的单调性得到的,因此对∀ y∈[0, b],

$\begin{matrix} \begin{matrix} U_{l} (i, b - y) = \\ \int_{0_{}}^{{b-y}_{}} f_{i - i} (x) \times U_{μ} (i, b - y - x) dx \leq \\ \int_{0_{}}^{{b-y}_{}} f_{i - i} (x) \times U_{μ} (i, b - y) dx = \\ U_{μ} (i, b - y) \times \int_{0_{}}^{{b-y}_{}} f_{i - i} (x) dx < \\ U_{μ} (i, b - y) \end{matrix} \end{matrix}$

其中第一个不等式成立是由累积概率分布函数的单调性得到的,第二个不等式成立是由于 $\begin{matrix} \int_{0_{}}^{{b-y}_{}} \end{matrix}$ f_i-i( x)d x<1。因为 μ^id={ x_i,…, x_d}的存在,所以 l^id={ x_i,…, x_i,…, x_d}不是 b-最可靠状态链,与假设相矛盾。

定理1表明可以通过基于动态规划的算法来求解自适应最可靠路径问题,因为 b-最可靠状态链满足动态规划的Bellman’s准则。随机网络环境下自适应最可靠路径问题可以推导为以下形式的问题:

For a given travel time budget b,

$\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x) =

$\begin{matrix} \max_{j \in Φ (i)} \end{matrix} \begin{matrix} \{\int_{0}^{b} f_{ij} (x) \times U_{_{μ^{*}}} (j, b - x) dx\} \end{matrix}$ ,

∀ i≠ d, x∈[0, b)

$\begin{matrix} μ_{(}^{*} \end{matrix}$ i, b-x) =

$\begin{matrix} \underset{j \in Φ (i)}{argmax} \end{matrix} \begin{matrix} \{\int_{0}^{b} f_{ij} (x) \times U_{_{μ^{*}}} (j, b - x) dx\} \end{matrix}$ ,

∀ i≠ d, x∈[0, b)

$\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( d, b-x) =1,∀ x∈[0, b)

μ^*( d, b-x) =d,∀ x∈[0, b)。

2 算法及计算复杂性分析

2.1 逐次逼近算法

本节设计基于动态规划的逐次逼近算法求解随机网络环境下自适应最可靠路径问题,如表1所示,给定行程时间预算 b,寻找 b-最可靠路径策略 μ^*( i, b),也就是选择下一个最优节点。

算法在第 k迭代时, $\begin{matrix} U_{μ}^{k} \end{matrix}$ ( i, b-x)表示根据路径策略 μ,从起点 i出发在行程时间预算 b-x内到达终点的概率,并且该路径不超过 k条边。 μ^k( i, b-x)表示根据 $\begin{matrix} U_{μ}^{k} \end{matrix}$ ( i, b-x)所得的下一个节点。 $\begin{matrix} U_{μ}^{k} \end{matrix}$ ( i, b-x)随着 k的增大不断接近最优值 $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x),并且近似误差随着 k的增大而减小,当 k的取值是最优路径所包含边的条数时 $\begin{matrix} U_{μ}^{k} \end{matrix}$ ( i, b-x) = $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)。

表1 算法ORRPP Table 1 Algorithm ORRPP

2.2 算法的计算复杂性分析

定理3 算法Algorithm ORRPP 的迭代次数是有限的。

证明一方面,由定理2可知, b-最可靠状态链不包含回路。另一方面,在每次迭代 k, $\begin{matrix} U_{μ}^{k} \end{matrix}$ ( i, b-x)表示根据路径策略 μ,从起点 i出发在行程时间 b-x内到达终点的概率,并且该路径包含不超过 k条边。所以 k不可能超过网络边的总数 $\begin{matrix} |A| \end{matrix}$ =m。

定理4 算法Algorithm ORRPP 的计算复杂度是 O( nb+nmb+mb²),其中 b表示区间[0, b)的长度, m是网络边的总数, n是网络节点的总数。

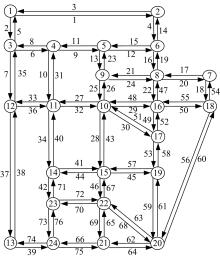
证明在Step0,初始化需要 O( nb)的计算复杂度。最复杂的情况是当 k= $\begin{matrix} |A| \end{matrix}$ =m时算法才终止,所以Step1 and Step2必须运行 k= $\begin{matrix} |A| \end{matrix}$ =m次。在Step1总的需要 O( b²)的计算复杂度。在Step2,判断终止条件需要 O( nb)的计算复杂度。所以算法Algorithm ORRPP总的计算复杂度为 O( nb) +m( O( b²) +O( nb))≈ O( nb+nmb+mb²)。

3 数值试验

本节数值实验的目标是通过实际网络Sioux falls (SF) network检验算法的可行性和正确性。所有算法都是通过MATLAB计算机语言编程并且在Windows-XP(64)工作站(two 2.00 GHz Xeon CPUs and 4G RAM)条件下运行的。Sioux Falls(SF)network的拓扑结构如图1所示^{[ 15]}。边的随机行程时间 $\begin{matrix} {\tilde{X}}_{ij} \end{matrix}$ 服从 Gamma( α_ij, β_ij)分布

f_ij( x) = $\begin{matrix} \frac{(β_{ij})^{α_{ij}} x^{α_{ij} - 1} e^{- β_{ij} x}}{Γ (α_{ij})} \end{matrix}$

其中: α_ij=0 .4log₁₀⁽¹⁰ ⁺⁰ ^.⁸ ⁱ⁺⁰ ^.⁷ ^j⁾;

β_ij=2log₁₀⁽¹² ⁺¹ ^.² ⁱ⁺⁰ ^.⁸ ^j⁾。

Gamma分布的期望值和方差分别是 α_ij/β_ij和 α_ij/ $\begin{matrix} (β_{ij})^{2} \end{matrix}$ 。

	Figure Option View Download New Window
	图1 苏福尔斯网络Fig.1 Sioux Falls network

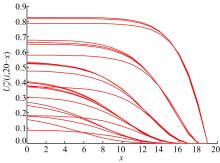
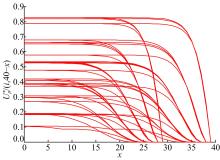
图2表示从节点 i=1,2,…,23时刻出发在 b-x( b=20)时间内到达终点 N=24的最大概率值 $\begin{matrix} U_{μ}^{*} \end{matrix}$ ( i, b-x)关于 x的函数图。图3表示从节点 i=1,2,…,23时刻出发在 b-x( b=30)时间内到达终点 N=24的最大概率值 $\begin{matrix} U_{μ}^{*} \end{matrix}$ ( i, b-x)关于 x的函数图。图4表示从节点 i=1,2,…,23时刻出发在 b-x( b=40)时间内到达终点 N=24的最大概率值 $\begin{matrix} U_{μ}^{*} \end{matrix}$ ( i, b-x)关于 x的函数图。

	Figure Option View Download New Window
	图2 $\begin{matrix} U_{μ}^{} \end{matrix}$ ( i,20 -x)关于 x的变化图Fig.2* $\begin{matrix} U_{μ}^{*} \end{matrix}$ ( i,20 -x) following the x

	Figure Option View Download New Window
	图3 $\begin{matrix} U_{μ}^{} \end{matrix}$ ( i,30 -x)关于 x的变化图Fig.3* $\begin{matrix} U_{μ}^{*} \end{matrix}$ ( i,30 -x) following the x

	Figure Option View Download New Window
	图4 $\begin{matrix} U_{μ}^{} \end{matrix}$ ( i,40 -x)关于 x的变化图Fig.4* $\begin{matrix} U_{μ}^{*} \end{matrix}$ ( i,40 -x) following the x

从以上的计算结果可以得出以下结论:

(1)函数 $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)在终点一致的情况下的取值不仅取决于起点的位置,而且取决于行程时间预算 b-x,函数 $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)的取值与起点、终点、时间预算 b-x取值都有关,是一个多元函数,这符合实际交通网络最可靠路径选择情形。

(2)在给定起点和终点的情况下,所有的 $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)都是关于 b-x的单调递减函数,这与理论推导是一致的,符合实际交通随机网络的情形。

(3)因为本算例中边的权值的概率分布函数都是假定为Gamma概率分布函数,所以当终点一致起点 i的位置相邻近时, $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)关于 x的函数非常接近。虽然在每个图中都有23条曲线,但是相邻点的 $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)关于 x的函数曲线图有一定的重合。连接起点和终点之间路径所包含节点数越多,则相应 $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)的函数值会越小。相反,连接起点和终点之间路径所包含节点数越少,则相应 $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)的函数值会越大。数值结果证实了这种趋势,从图中可以看出,从23个起点出发的23条曲线分成了4或者5类。起点离终点越远则相应的概率 $\begin{matrix} U_{_{μ^{*}}} \end{matrix}$ ( i, b-x)取值越低。

4 结论

研究了基于可靠性理论的随机交通网络自适应最可靠路径问题。证明了该问题满足动态规划的Bellman's 准则, 构造了逐次逼近算法求解该问题。通过对实际交通网络的计算对提出的方法进行了验证。结果表明, 结合用户的不同行程时间预算,提出的算法可以获得随机交通网络的最可靠路径。但是,本文只考虑了行程时间的随机特性, 没有涉及动态特性, 动态随机交通网络环境下最可靠路径问题需要进一步研究。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	黄卫, 张宁. 智能交通系统理论研究与实践[M]. 南京: 江苏科学技术出版社, 2011. [本文引用:1]
[2]	杨兆升. 城市交通流诱导系统理论与模型[M]. 北京: 人民交通出版社, 2000. [本文引用:1]
[3]	Hall R W. The fastest path through a network with rand om time-dependent travel times[J]. Transportation Science, 1986, 20(3): 182-188. [本文引用:1] [JCR: 1.814]
[4]	Schrank D, Lomax T. The 2012 annual urban mobility report[R]. Texas: Texas Transportation Institute, The Texas A&M University, 2012. [本文引用:1]
[5]	Gao S, Chabini I. Optimal routing policy problems in stochastic time-dependent networks[J]. Transportation Research Part B: Methodological, 2006, 40(2): 93-122. [本文引用:1] [JCR: 2.944]
[6]	Miller-Hooks E D. Adaptive least-expected time paths in stochastic, time-varying transportation and data networks[J]. Networks, 2001, 37(1): 35-52. [本文引用:1] [JCR: 0.645]
[7]	Miller-Hooks E D, Mahmassani H S. Least expected time paths in stochastic, time-varying transportation networks[J]. Transportation Science, 2000, 34(2): 198-215. [本文引用:1] [JCR: 1.814]
[8]	Huang H, Gao S. Optimal paths in dynamic networks with dependent rand om link travel times[J]. Transportation Research Part B: Methodological, 2012, 46(5): 579-598. [本文引用:1] [JCR: 2.944]
[9]	Gao S, Huang H. Real-time traveler information for optimal adaptive routing in stochastic time-dependent networks[J]. Transportation Research Part C: Emerging Technologies, 2012, 21(1): 196-213. [本文引用:1] [JCR: 2.006]
[10]	Wu X, Nie Y. Modeling heterogeneous risk-taking behavior in route choice: a stochastic dominance approach[J]. Transportation Research Part A, 2011, 45(9): 896-915. [本文引用:1]
[11]	Miller-Hooks E D, Mahmassani H S. Path comparisons for a priori and time-adaptive decisions in stochastic, time-varying networks[J]. European Journal of Operational Research, 2003, 146(2): 67-82. [本文引用:1] [JCR: 2.038]
[12]	Miller-Hooks E D, Mahmassani H S. Least possible time paths in stochastic, time-varying transportation networks[J]. Computers & Operations Research, 1998, 25(12): 1107-1125. [本文引用:1]
[13]	Nie Y M, Wu X. Reliable a Priori Shortest Path Problem with Limited Spatial and Temporal Dependencies [M]. Transportation and traffic theory 2009: golden jubilee. Springer US, 2009: 169-195. [本文引用:1]
[14]	张志华. 可靠性理论及工程应用[M]. 北京: 科学出版社, 2012. [本文引用:1]
[15]	Bar-Gera H. Transportation network test problems website[EB/OL]. http://www.bgu.ac.jl/~bargera/tntp/.2011-1-1/2013-12-1. [本文引用:1]

2011

0.0

... 智能交通系统是解决现代社会交通需求与交通供给两者之间矛盾的重要途径之一^[1] ...

2000

0.0

1986

1.814

0.0

... 随机路径分为两种路径:先验路径和自适应路径,Hall^[3]在1986年指出自适应路径比先验路径更优,并且给出了小的算例验证了该定理的正确性 ...

2012

0.0

... 例如,将交通网络中通过某路段的时间耗费看作网络中边的权值,该网络边的权值是不确定的,是一个服从一定概率分布函数的随机变量^[4] ...

2006

2.944

0.0

. 2006, 40(2):null-null

Optimal routing policy problems in stochastic time-dependent networks

... 2006年Gao and Chabini^[5]和2012年Gao and Huang^[8]也对这个结论给出了验证 ...

2001

0.645

0.0

. 2001, 37(1):35-52

Adaptive least-expected time paths in stochastic, time-varying transportation and data networks

Elise Miller-Hooks *

Department of Civil & Environmental Engineering, 212 Sackett Building, The Pennsylvania State University University Park, Pennsylvania 16802<br/><sup>*</sup>Department of Civil & Environmental Engineering, 212 Sackett Building, The Pennsylvania State University University Park, Pennsylvania 16802

In congested transportation and data networks, travel (or transmission) times are time-varying quantities that are at best known a priori with uncertainty. In such stochastic, time-varying (or STV) networks, one can choose to use the a priori least-expected time (LET) path or one can make improved routing decisions en route as traversal times on traveled arcs are experienced and arrival times at intermediate locations are revealed. In this context, for a given origin-destination pair at a specific departure time, a single path may not provide an adequate solution, because the optimal path depends on intermediate information concerning experienced traversal times on traveled arcs. Thus, a set of strategies, referred to as hyperpaths, are generated to provide directions to the destination node conditioned upon arrival times at intermediate locations. In this paper, an efficient label-setting-based algorithm is presented for determining the adaptive LET hyperpaths in STV networks. Such a procedure is useful in making critical routing decisions in Intelligent Transportation Systems (ITS) and data communication networks. A side-by-side comparison of this procedure with a label-correcting-based algorithm for solving the same problem is made. Results of extensive computational tests to assess and compare the performance of both algorithms, as well as to investigate the characteristics of the resulting hyperpaths, are presented. An illustrative example of both procedures is provided. © 2001 John Wiley & Sons, Inc.

2000

1.814

0.0

2012

2.944

0.0

. 2012, 46(5):null-null

Optimal paths in dynamic networks with dependent random link travel times

... 2006年Gao and Chabini^[5]和2012年Gao and Huang^[8]也对这个结论给出了验证 ...

2012

2.006

0.0

. 2012, 21(1):null-null

Real-time traveler information for optimal adaptive routing in stochastic time-dependent networks

2011

0.0

. 2011, 45(9):896-915 DOI:10.1016/j.tra.2011.04.009

Modeling heterogeneous risk-taking behavior in route choice: a stochastic dominance approach

Abstract

This paper proposes a unified approach to modeling heterogonous risk-taking behavior in route choice based on the theory of stochastic dominance (SD). Specifically, the first-, second-, and third-order stochastic dominance (FSD, SSD, TSD) are respectively linked to insatiability, risk-aversion and ruin-aversion within the framework of utility maximization. The paths that may be selected by travelers of different risk-taking preferences can be obtained from the corresponding SD-admissible paths, which can be generated using general dynamic programming. This paper also analyzes the relationship between the SD-based approach and other route choice models that consider risk-taking behavior. These route choice models employ a variety of reliability indexes, which often make the problem of finding optimal paths intractable. We show that the optimal paths with respect to these reliability indexes often belong to one of the three SD-admissible path sets. This finding offers not only an interpretation of risk-taking behavior consistent with the SD theory for these route choice models, but also a unified and computationally viable solution approach through SD-admissible path sets, which are usually small and can be generated without having to enumerate all paths. A generic label-correcting algorithm is proposed to generate FSD-, SSD-, and TSD-admissible paths, and numerical experiments are conducted to test the algorithm and to verify the analytical results.

Research highlights

? A unified approach is proposed to model heterogonous risk-taking behavior in route choice based on the theory of stochastic dominance (SD). ? Optimal paths for many existing reliability-based route choice models belong to one of the three SD-admissible path sets. ? SD-admissible path sets can be generated without having to enumerate all paths. ? A unified and computationally viable solution approach is proposed to generate SD-admissible path sets.

2003

2.038

0.0

. 2003, 146(2):null-null

Path comparisons for a priori and time-adaptive decisions in stochastic, time-varying networks

1998

0.0

2009

0.0

2012

0.0

... 可靠度作为可靠性理论的重要指标,在工程上已经得到了广泛应用^[14] ...

0.0

... Sioux Falls(SF)network的拓扑结构如图1所示^[15] ...