1990年,我国首座钢管混凝土拱桥——四川省广元市旺苍东河大桥建成通车。此后,钢管混凝土拱桥迅速发展,2000年后成为中国公路拱桥修建之首。据文献[1]统计,已建钢管混凝土拱桥中,56.3%的跨径超过百米,属大跨径桥梁。

相比于大跨钢管混凝土拱桥在工程中的广泛应用,其抗震性能的研究及抗震设计规程规范较为滞后。我国现行公路工程抗震设计规范于1990年开始施行,仅适用于主跨不超过150 m的梁桥和拱桥,对于一座已建成通车的钢管混凝土拱桥,其抗震设计在规范中尚未考虑;美国AASHTO的抗震设计则明确指出,该规范只适用于主跨不超过150 m的普通钢或混凝土梁桥;欧洲规范及日本的桥梁规范均适用于跨度不超过200 m的桥梁^{[ 2]}。我国于2008年对《公路工程抗震设计规范》(JTJ004-89)的桥梁抗震设计部分进行了修订,颁布了《公路桥梁抗震设计细则》(JTG/T B02-01-2008),细则中对单跨跨径超过150 m的特大跨径拱桥给出了抗震设计原则,且对位于抗震设防烈度大于9度地区的桥梁和有特殊要求的大跨径或特殊桥梁,细则规定其抗震设计应做专门研究,按有关规定执行。简言之,处于抗震设防烈度超过8度地区的大跨径桥梁,仍没有相应规范以供参考。

纵观国内近年来的几次大地震:2008年5月12日,四川汶川发生8.0级地震,地震烈度达11度;2010年4月14日,青海玉树发生7.1级地震,地震烈度达9度;2013年4月20日,四川雅安发生7.0级地震,地震烈度达9度。地震发生后,道路桥梁的损毁程度以及对其修复的速度极大程度上决定着救援工作的成败。因此,急需研究分析大跨钢管混凝土拱桥在强震作用下的抗震性能,通过弹塑性时程分析得出地震作用各时刻结构的内力及变形状态,给出结构塑性发展的部位、方向和顺序,发现应力和塑性变形集中的部位,从而判断结构的屈服机制、薄弱环节及可能的破坏模式,以此作为大跨钢管混凝土拱桥进行正确有效抗震设计的理论依据,对钢管混凝土拱桥的抗震设计给出指导。

根据现有文献,大跨钢管混凝土拱桥的研究多集中于静力稳定性分析和地震作用下的结构内力、位移响应的求解上,鲜有研究者把抗震性能的研究与大跨钢管混凝土拱桥的动力稳定性联系起来。本文针对大跨钢管混凝土拱桥自身的动力特性,由某大跨钢管混凝土拱桥强震作用下的弹塑性时程分析入手,从动力稳定性的角度出发,研究桥梁结构在强震作用下的动力破坏过程,确定其破坏模式及机理。

由于外部作用与时间参数间关系的多样性,结构的动力稳定问题远比静力稳定问题复杂,但研究者对动力稳定问题的认识却同样遵循着由分叉问题到极值问题的演变。根据经典Liapunov弹性动力稳定性理论,动力屈曲是指离散时间点上的动力分叉解。由上述弹性动力屈曲概念,依据地震波持续时间及时间间隔的不同,结构在一个地震持时内可能出现有限个动力平衡状态,得出结构在某个时间点或区段上稳定而在其他时间点或区段上不稳定的结论,据此结论结构的最终状态可能是稳定的或是不稳定的。但是,结构在强震作用下的稳定—不稳定—倒塌是一个必然的过程,在此过程中惯性力与阻尼力阻碍结构变形的发展,结构倒塌前可能会有塑性变形的发生和发展,并伴随结构刚度下降和内力重分布的产生,结构的稳定临界荷载及失稳模式随之改变,动力稳定由弹性的动力分叉问题转化为涉及材料及变形双重非线性的动力极值问题^{[ 3, 4]}。

计入非线性因素后的动力失稳机理复杂,尚没有统一的动力稳定性判别准则,而判别准则的选取对动力稳定性分析起着决定性作用。本文选用了为许多学者所接受的B-R准则,该准则与静力稳定理论中的二类稳定问题相近,直接求解运动方程得到荷载-位移关系;将荷载的微小增量导致位移剧烈变化时的荷载定义为结构的动力稳定性临界荷载^{[ 4]}。

B-R准则源于阶跃荷载下浅球壳结构的动力稳定分析,可是地震作用输入的不确定性使其比阶跃荷载的模拟要复杂。为实现地震作用下结构性能的分析,近年常用动态增量法(Incremental dynamic analysis,IDA)来模拟不同强度的地震波,思路与静力pushover相近。按照IDA,引入一系列调整系数对地震加速度进行放大或缩小,并对由此得到的这组地震动作用下的结构进行时程分析,通过结构性能参数与地震峰值加速度水平之间的关系评价结构的抗震性能^{[ 5, 6]}。

本文以一座中承式钢管混凝土拱桥为例,建模过程中涉及的主要参数详见 表1^{[ 7]}。建模过程中,以双线性随动强化模型定义钢管混凝土拱肋的材料特性^{[ 8, 9]},其余构件材料均为弹性;除吊杆采用空间杆元,桥面板采用空间壳元以外,其余构件均以空间梁元模拟,全桥空间有限元模型见 图1。

表1

Table 1

表1(Table 1)

表1 全桥模型主要参数 Table 1 Key parameters of FEM 名称 参数 说明 跨度 360 m 计算跨径,344 m 拱肋轴线 m=2、 k=1.317 悬链线 拱肋弦管 外钢管:⌀750 mm×18 mm 核心混凝土:C50 CFST 横撑-弦杆 ⌀500 mm×12 mm 圆钢管 横撑-腹杆 ⌀350 mm×10 mm 圆钢管 立柱 外钢管:⌀1000 mm×20 mm 核心混凝土:C30 CFST 吊杆 91根⌀7镀锌高强钢丝束 fu=1670 MPa 横梁 工字形变截面钢梁 按刚度等效, 等截面梁模拟 桥面板 厚度22 cm 预制RC板,考虑其上 12 cm厚铺装层自重

表1 全桥模型主要参数 Table 1 Key parameters of FEM

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 有限元模型Fig.1 Finite element model

钢管混凝土拱肋双线性随动强化模型主要参数包括钢管混凝土组合轴压强度标准值 fscy、弹性组合模量 E_sc及强化段组合模量 Esch,分别按下列公式式取值。

fscy=1.212+Bξ+Cξ2fck1式中:B=0.1759fy/235+0.974C=-0.1038fck/20+0.0309

式中: ξ为套箍系数 A_s f_y /A_c f_ck; f_ck, f_y分别为混凝土轴心抗压强度标准值及钢材屈服强度值, A_s, A_c分别为钢管及核心混凝土的截面积。

Esc=fscp/εscp2

式中: fscp为钢管混凝土轴压组合比例极限,其表达式为:

fscp=0.192(fy/235)+0.488fscy

钢管混凝土强化段组合模量仅与套箍系数有关,按下式求得,

ξ≥1时,Esch=420ξ+550(3)ξ<1时,Esch=400ξ-150(4)

本文借助ANSYS软件,将El-centro地震加速度作为基本地震动输入,以0.1 g为增量,结合IDA方法对算例进行三维地震作用下的时程分析。首先对算例进行仅考虑几何非线性的弹性时程分析,当由拱肋单元应力确定构件进入弹塑性工作阶段后,开始进行考虑双重非线性的弹塑性时程分析。当两级地震动输入之间特征响应变化剧烈,且伴随有拱肋节点位移时程的发散时,则定义此时的结构动力失稳,对应的地震峰值加速度为结构的动力稳定极限承载力。

3.2 算例时程分析结果及其抗震性能

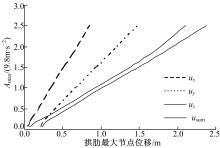
分析结果表明,峰值加速度( A_max)达1.49 g以前,拱肋处于弹性工作阶段,拱肋节点各向位移最大值、拱肋应变能峰值及单元应变能峰值均随地震动峰值加速度的增大而大。地震波峰值加速度达0.25 g之前,拱肋节点位移由竖向位移所占比重最大逐渐转化为竖位移与横向位移所占比重相当,0.25 g之后拱肋横向位移的增大幅度显著高于其他两个方向的位移分量,拱肋节点位移逐渐以拱肋横向位移为主(详见 图2)。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 拱肋最大节点位移IDA曲线Fig.2 IDA curve for displacement maximums

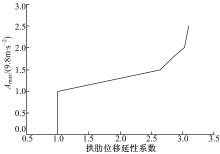
当 A_max达1.49 g时,经过11.68 s,在左拱脚处拱肋杆件首先产生塑性变形,标志拱肋进入弹塑性工作阶段。由 图3、 图4可见,相应的拱肋塑性应变能峰值IDA曲线

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 拱肋塑性应变能峰值IDA曲线Fig.3 IDA curve for peak plastic strain energy in arch-rib

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 单元塑性应变能峰值IDA曲线Fig.4 IDA curve for peak plastic strain energy of elements

及单元塑性应变能峰值IDA曲线均出现明显折点;由 图5、 图6可见,拱肋应变能峰值IDA曲线及单元应变能IDA曲线的斜率明显减小;拱肋最大节点位移基本随地震峰值加速度的增大呈线性增长,拱肋最大节点位移达1.48 m,节点位移延性系数为2.6( 图7)。峰值加速度达1.5 g时,左拱脚处拱肋截面塑性程度加深,杆件内积蓄的塑性应变能为1.49 g时的18倍,但沿拱肋跨度方向的塑性程度无进一步的发展。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 拱肋应变能峰值IDA曲线Fig.5 IDA curve for peak strain energy in arch-rib

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 单元应变能峰值IDA曲线Fig.6 IDA curve for peak strain energy of elements

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 拱肋位移延性系数IDA曲线Fig.7 IDA curve for ductility factor of arch-rib displacement

A_max为1.8 g时,结构刚度进一步降低,此时拱肋节点位移继续增加且以横向变形为主,拱顶总位移达到1.76 m(其中横向位移分量为1.63 m)。与 A_max为1.49 g时相比,拱肋进入弹塑性工作阶段的时间明显提前,截面塑性发展程度更深,沿结构跨度方向塑性区域加大。具体过程如下:3.08 s时左拱脚处拱肋首先进入塑性;3.76 s时,拱肋与立柱交汇处(左)进入塑性;7.04 s时右拱脚处拱肋截面进入塑性,此时拱肋塑性应变能峰值约为 A_max=1.49 g时的1467.8倍,由 图3、 图4可见,此时曲线斜率明显变小。相应的应变能峰值IDA曲线斜率继续减小,拱肋延性系数为2.9。

随 A_max的继续增加,拱肋进入塑性的时间继续提前,截面及构件直至整个拱肋的塑性发展程度逐步加深。 A_max增至2.0 g时,左拱脚于3.02 s即进入塑性,之后左1/4跨处杆件于3.62 s时进入塑性;持时达3.70 s、5.08 s时,拱肋与桥面交汇处、距离左拱脚5/6跨处相继产生塑性变形;7.00 s,右拱脚处杆件进入塑性,且此时拱肋塑性应变能增至1.49 g时的4729.9倍,相应IDA曲线的斜率继续减小,各指标曲线增长更为迅速。延性系数为3.0,拱顶处最大节点位移达到1.93 m,而横向位移分量为1.78 m。

当 A_max=2.5 g时,左拱脚处拱肋更早进入塑性(1.64 s),沿跨度方向拱肋塑性区域进一步扩大。左右拱脚、1/4及3/4跨、拱肋与桥面交汇处、1/6及5/6跨等处杆件及其附件杆件先后进入塑性,拱肋塑性应变能达2527342J,约为 A_max=1.49 g时的2万余倍。拱肋最大节点位移在拱顶附近,达到2.37 m,此时的拱肋延性系数为3.1。 A_max增加至2.55 g时,拱肋最大节点位移达到3.56 m,拱肋节点位移响应于5.08 s迅速发散,说明结构已无法维持原有位形继续承受地震作用,拱肋节点位移急剧增长发生动力失稳破坏。由本文对动力稳定极限承载力的定义,此算例的动力极限荷载为2.5 g。

综上,地震动峰值加速度越大,拱肋构件越早进入塑性,拱肋塑性发展程度越深,结构刚度削弱越大,拱肋节点位移随之逐渐加大。当地震动强度足够大时,结构最终会由于急剧增大的位形变化无法继续承受地震的作用而导致动力失稳破坏。弹塑性时程分析的结果表明,当拱肋最大节点位移尚未发生急剧变化时,拱肋塑性应变能就已经在 A_max达到1.8 g、2.0 g时出现了较大增长,相应塑性应变能IDA曲线明显转折。并且,在 A_max的增长过程中,拱肋最大节点位移始终发生在拱顶及其附近,而拱脚则一直是拱肋塑性开展的起点和塑性发展程度最深的位置,可见应依靠多项响应指标,从宏观和微观两个方面入手才能较为全面地评价大跨钢管混凝土拱桥的抗震性能。

本文借助ANSYS软件,采用IDA方法输入具有不同峰值加速度的地震波(基本地震波为El-centro波),对一大跨钢管混凝土拱桥进行了三维弹塑性时程分析,引入多个响应指标依据B-R准则最终确定了本文算例在地震作用下的动力稳定极限承载力。通过分析得出以下结论:

(1)拱肋节点位移随地震动峰值加速度的提高而加大,最大位移发生在拱顶及其附近位置,且以横向位移为主。当峰值加速度足够大时,结构最终由于位形的急剧变化无法继续承受地震作用,发生动力失稳破坏。

(2)地震动峰值加速度越大,拱肋越早进入弹塑性工作阶段,拱肋塑性开展程度越深,在拱肋节点位移急剧增大之前,拱肋塑性应变能有明显提高。

(3)就本文算例而言,在拱肋进入弹塑性工作阶段以后,随地震动峰值加速度的提高,拱肋位移延性系数基本维持在3.0左右。可见,峰值加速度对于结构构件进入弹塑性工作阶段后的变形增长无显著影响。

由于桥梁工程在灾后救援中的重要地位,对于桥梁工程大震不倒的理解应为“地震后可能产生较大破坏,但不出现整体倒塌,经抢修后可限速通车,结构处于弹塑性工作阶段”而非“在大震作用下,结构物可能产生重大破坏,但不致倒塌”^{[ 2]}。从这个角度出发,对于大跨钢管混凝土拱桥强震下抗震性能的研究更应该从位移和能量两个角度入手,不仅要控制变形更要控制主要结构构件塑性变形的位置及其发展深度,以达到桥梁的灾后抢修和快速恢复通车的目的。