四轴抛光平台综合误差建模及分析

引用本文

赵帼娟, 张雷, 卢磊, 韩飞飞, 赵继. 四轴抛光平台综合误差建模及分析. 44(6): 1676-1683
ZHAO Guo-juan, ZHANG Lei, LU Lei, HAN Fei-fei, ZHAO Ji. Modeling and analysis of the volumetric errors of four-axis polishing platform. Journal of Jilin University Engineering and Technology Edition, 44(6): 1676-1683 复制到剪切板

Permissions

四轴抛光平台综合误差建模及分析

赵帼娟, 张雷, 卢磊, 韩飞飞, 赵继

吉林大学机械科学与工程学院,长春 130022

通信作者:张雷( 1970-),男,教授,博士生导师.研究方向:智能精密制造.E-mail:zhanglei@jlu.edu.cn

作者简介:赵帼娟(1987-),女,博士研究生.研究方向:智能精密制造.E-mail:zhaogj09@mails.jlu.edu.cn

基金:“973”国家重点基础研究发展计划项目(2011CB706702);

摘要

针对两个直线电机驱动的以气浮平台和两个旋转台为主要运动单元的四轴抛光系统,利用多体系统理论,建立了同时考虑位置误差和方向误差的综合误差模型。运用激光干涉仪对气浮平台各单项几何误差和旋转台的定位误差进行测量。对测量结果分析发现,气浮平台定位误差没有明显的线性增加或减小的趋势,竖直直线度大于定位误差和水平直线度,与传统滚珠丝杠驱动的运动平台误差相比有很大的不同。通过将试验与理论相结合的定量研究,得到了在气浮平台单项几何误差及其相互之间的垂直度误差共同影响下的两轴联动工况下综合误差的位置和方向分量,发现气浮平台综合误差竖直方向的分量很显著,揭示了气浮平台产生几何误差的原因,为抛光平台的几何误差补偿提供了理论依据。

关键词: 机床; 气浮平台; 综合误差; 几何误差; 多体系统

中图分类号:TH161 文献标志码:A 文章编号:1671-5497(2014)06-1676-08

Modeling and analysis of the volumetric errors of four-axis polishing platform

ZHAO Guo-juan, ZHANG Lei, LU Lei, HAN Fei-fei, ZHAO Ji

College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

Abstract

The volumetric error of a four-axis polishing platform with two aerostatic stages driven by linear motors and two rotational stages is modeled considering both position error and direction error by multi-body system theory. The individual geometric errors of the motion parts are measured by laser interferometer. The measuring results indicate that, for aerostatic stage, the position error shows neither linear increasing nor decreasing trend; the vertical straightness is larger than the position error and the vertical st4aightness, which is obviously different from the errors of traditional ball screw driven platform. The position component and direction component of the volumetric error of the resultant motion of two linear axes are investigated theoretically and experimentally considering the comprehensive influence of the individual geometric errors of the aerostatic stages. It is found that the vertical component of the volumetric error of the aerostatic stage is obvious. The causes of the geometric errors of the aerostatic stages are revealed, which provides the theoretical basis for geometric error compensation of the polishing platform.

Keyword: machine tool technology; aerostatic stage; volumetric error; geometric error; multi-body system

Show Figures

0 引言

随着现代制造技术的飞速发展,精密、超精密加工应用广泛,对数控机床的加工精度提出了更高的要求。而机床的加工精度是由刀具与工件之间的相对位移决定的,刀具与工件之间的综合误差(位置和方向误差)会影响刀具与工件间相对位姿,要提高机床加工精度必须对机床误差进行补偿^{[ 1, 2]}。误差补偿需要对误差来源及其作用规律建模分析,以提高误差补偿的准确性和效率。目前,以多体系统理论为基础的误差建模分析方法被广泛应用。国内外学者有关数控机床误差建模、分析和补偿方法的研究取得了很大进展,并将研究重点由传统的三轴数控机床转向五轴数控机床^{[ 3, 4, 5, 6, 7, 8, 9]},但是相关研究仍集中在滚珠丝杠副传动方式引起的数控机床运动误差建模和补偿方面。

直线电机驱动气浮平台的传动方式越来越多地应用在半导体制造设备、超精密机床和测量仪器上,气浮平台自身的运动误差直接影响系统的性能,最终影响加工和测量精度^{[ 10]}。文献[11]对精密线性气浮平台各单项运动误差进行了测量和分析。文献[12-13]在对气体静压导轨精度研究中,重点对气体静压导轨表面轮廓误差与几何误差之间的关系进行了理论和试验研究,在二维条件下分析了导轨轮廓误差、供气压与竖直方向的直线度误差、俯仰误差之间的耦合关系。文献[14]基于多体系统理论建立了两个线性气浮导轨系统的综合误差模型,并在该模型基础上应用小波理论对误差进行相关性分析,进一步识别系统误差源。

本文应用多体系统理论对研发的四轴抛光平台(该平台以两个直线电机驱动的气浮平台和两个旋转台为主要运动单元)建立了同时考虑位置误差和方向误差的综合误差模型,利用激光干涉仪对平台主要运动部件的各单项几何误差(定位误差、直线度、转角误差等)进行测量,并将获得的气浮平台的单项误差与传统的滚珠丝杠驱动的运动平台单项误差进行了对比。发现由直线电机驱动的气浮平台竖直方向的直线度和综合误差分量很显著。理论分析结果显示当存在两个转动副做四轴联动时,转动副转动角度以及角度误差会对位置误差产生耦合影响。最后将单项几何误差测量结果代入综合误差模型,得到抛光平台位置误差和方向误差的分布规律。

1 综合误差模型建立

1.1 四轴抛光平台拓扑结构及坐标系建立

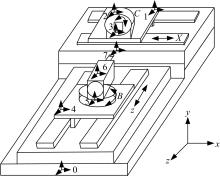
图1为研发的四轴抛光平台结构简图。 X、 Z轴拖板相互垂直, Y轴由右手定则确定。 B轴转台安装在 Z轴拖板上, C轴转台安装在 X轴拖板上。刀具安装在主轴上,工件安装在 C轴转台上。

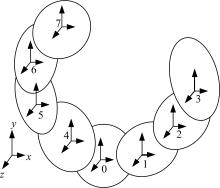
	Figure Option View Download New Window
	图1 四轴抛光平台结构简图Fig.1 Sketch of four-axis polishing platform

建立抛光平台拓扑结构如图2所示。为了建模方便,所有坐标系均采用右手笛卡尔坐标系。规定移动误差正负与坐标轴方向相同。转角误差正负按右手螺旋定则确定。对于工件链:在床身(惯性体0)上建立参考坐标系0;在 X轴拖板(低序体1)上建立坐标系1;在工件转台( C轴,低序体2)上建立坐标系2;在工件(低序体3)上建立坐标系3。对于刀具链:在 Z轴拖板(低序体4)上建立坐标系4;在主轴转台( B轴,低序体5)上建立坐标系5;在主轴(低序体6)上建立坐标系6;在刀具(低序体7)上建立坐标系7。

	Figure Option View Download New Window
	图2 抛光平台拓扑结构Fig.2 Topology structure of polishing platform

机床几何误差包括制造和装配误差、工件和刀具安装误差、运动副误差和热变形误差等。为了消除空间误差模型中的偏移,使模型复杂度降低,基于刚体假设,本文不考虑机床受热变形、刀具和工件安装误差的影响,并且假设主轴与主轴转台固定无相对运动误差,刀具与主轴固定无相对运动误差。规定转换矩阵的方向为从工件坐标系转换到刀具坐标系,以及垂直度误差的基准为 X轴,垂直度误差以两轴正向夹角增大为正。

1.2 相邻体间变换矩阵

(1)理想无误差条件下相邻体间变换矩阵

设 X、 Z轴分别移动 x、 z, B轴、 C轴分别转动 θ_B、 θ_C。

工件链:从参考坐标系0到 X轴拖板坐标系1的齐次变换矩阵为 T_01, _i;从 X轴拖板坐标系1到 C轴坐标系2的齐次坐标变换矩阵为 T_12, _i;工件与 C轴无相对运动,因此从坐标系2到坐标系3的齐次坐标变换矩阵 T_23, _i为单位矩阵。

$\begin{matrix} \begin{matrix} T_{01, i} = [\begin{matrix} 1 & 0 & 0 & x \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (1) \\ T_{12 i} = [\begin{matrix} \cos θ_{C} & - \sin θ_{C} & 0 & 0 \\ \sin θ_{C} & \cos θ_{C} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (2) \\ T_{23, i} = I_{4 \times 4} (3) \end{matrix} \end{matrix}$

刀具链:从参考坐标系0到 Z轴拖板坐标系4的齐次变换矩阵为 T_04, _i;从 Z轴拖板坐标系4到 B轴坐标系5的齐次坐标变换矩阵为 T_45, _i;主轴与 C轴无相对运动、刀具与主轴无相对运动,因此从坐标系5到坐标系6的齐次坐标变换矩阵 T_56, _i、坐标系6到坐标系7的齐次坐标变换矩阵 T_67, _i均为单位矩阵。

$\begin{matrix} \begin{matrix} T_{04 i} = [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & z \\ 0 & 0 & 0 & 1 \end{matrix}] (4) \\ T_{45, i} = [\begin{matrix} \cos θ_{B} & 0 & \sin θ_{B} & 0 \\ 0 & 1 & 0 & 0 \\ - \sin θ_{B} & 0 & \cos θ_{B} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] (5) \\ T_{56, i} = T_{67, i} = I_{4 \times 4} (6) \end{matrix} \end{matrix}$

理想无误差条件下,刀具和工件两个典型体之间的齐次坐标变换矩阵为:

$\begin{matrix} \begin{matrix} T_{37, i} = {[T_{01 i} T_{12, i} T_{23, i}]}^{- 1} T_{04, i} T_{45, i} T_{56, i} T_{67, i} = \\ [\begin{matrix} \cos θ_{B} \cos θ_{C} & \sin θ_{C} & \sin θ_{B} \cos θ_{C} & - xcos θ_{C} \\ - si n θ_{C} \cos θ_{B} & \cos θ_{C} & - \sin θ_{B} \sin θ_{C} & xsin θ_{C} \\ - \sin θ_{B} & 0 & \cos θ_{B} & z \\ 0 & 0 & 0 & 1 \end{matrix}] (7) \end{matrix} \end{matrix}$

(2)存在运动误差条件下相邻体间误差变换矩阵为:

$\begin{matrix} Δ T_{01, e} = [\begin{matrix} 1 & - ε_{zX} & ε_{yX} & δ_{xX} \\ ε_{zX} & 1 & - ε_{xX} & δ_{yX} \\ - ε_{yX} & ε_{xX} & 1 & δ_{zX} \\ 0 & 0 & 0 & 1 \end{matrix}] (8) \end{matrix}$

式中: T_01, _e表示存在运动误差条件下 X轴拖板移动 x时从参考坐标系0到 X轴拖板坐标系1的误差变换矩阵; δ_xX、 δ_yX、 δ_zX、 ε_xX、 ε_yX、 ε_zX分别为定位误差、竖直直线度误差、水平直线度误差、滚转角误差、偏摆角误差和俯仰角误差。

$\begin{matrix} Δ T_{12, e} = [\begin{matrix} 1 & - ε_{z θ_{C}} & ε_{y θ_{C}} & δ_{x θ_{C}} \\ ε_{z θ_{C}} & 1 & - ε_{x θ_{C}} & δ_{y θ_{C}} \\ - ε_{y θ_{C}} & ε_{x θ_{C}} & 1 & δ_{z θ_{C}} \\ 0 & 0 & 0 & 1 \end{matrix}] (9) \end{matrix}$

式中: ΔT_12, _e表示存在运动误差条件下 C轴转动 θ_C时从 X轴拖板坐标系1到 C轴坐标系2的误差变换矩阵; δ_xθC、 δ_yθC、 δ_zθC、 ε_xθC、 ε_yθC、 ε_zθC分别为 C轴转动 θ_c角度时,沿 x轴径向误差、沿 y轴径向误差、沿 z轴轴向误差、两个倾斜角误差和定位误差。

$\begin{matrix} Δ T_{04, e} = [\begin{matrix} 1 & - ε_{zZ} & ε_{yZ} & δ_{xZ} - z S_{xZ} \\ ε_{zZ} & 1 & - ε_{xZ} & δ_{yZ} \\ - ε_{yZ} & ε_{xZ} & 1 & δ_{zZ} \\ 0 & 0 & 0 & 1 \end{matrix}] (10) \end{matrix}$

式中: ΔT_04, _e表示存在运动误差条件下 Z轴拖板移动 z时从参考坐标系0到 Z轴拖板坐标系4的误差变换矩阵; δ_xZ、 δ_yZ、 δ_zZ、 ε_xZ、 ε_yZ、 ε_zZ分别为 Z轴拖板运动时水平直线度误差、竖直直线度误差、定位误差、俯仰角误差、偏摆角误差和滚转角误差。 S_xZ为 Z轴与 Z轴的垂直度误差。

$\begin{matrix} \begin{matrix} Δ T_{45, e} = [\begin{matrix} 1 & - ε_{z θ_{B}} & ε_{y θ_{B}} & δ_{x θ_{B}} \\ ε_{z θ_{B}} & 1 & - ε_{x θ_{B}} & δ_{y θ_{B}} \\ - ε_{y θ_{B}} & ε_{x θ_{B}} & 1 & δ_{z θ_{B}} \\ 0 & 0 & 0 & 1 \end{matrix}] \\ (11) \end{matrix} \end{matrix}$

式中: ΔT_45, _e表示存在运动误差条件下 B轴转动 θ_B时从 Z轴拖板坐标系4到 B坐标系5的误差变换矩阵; $\begin{matrix} δ_{x θ_{B}} \end{matrix}$ 、 $\begin{matrix} δ_{y θ_{B}} \end{matrix}$ 、 $\begin{matrix} δ_{z θ_{B}} \end{matrix}$ 、 $\begin{matrix} ε_{x θ_{B}} \end{matrix}$ 、 $\begin{matrix} ε_{y θ_{B}} \end{matrix}$ 、 $\begin{matrix} ε_{z θ_{B}} \end{matrix}$ 分别为 B轴转动 θ_B角度时, x向径向误差、 y向径向误差、 z向径向误差、 x向倾斜角误差、 y向倾斜角误差和 z向倾斜角误差。

实际存在误差条件下,刀具和工件两个典型体之间的齐次坐标变换矩阵为:

$\begin{matrix} \begin{matrix} T_{37} = {[T_{01 i} Δ T_{01, e} T_{12, i} Δ T_{12, e} T_{23, i}]}^{- 1} T_{04, i} Δ T_{04, e} \times \\ T_{45, i} Δ T_{45, e} T_{56, i} T_{67, i} (12) \end{matrix} \end{matrix}$

(3)基于小误差假设,工件坐标系3到刀具坐标系7的综合误差变换矩阵为^{[ 15]}:

$\begin{matrix} \begin{matrix} ΔE = T_{37} - T_{37, i} = \\ [\begin{matrix} 1 & - Δ ε_{z} & Δ ε_{y} & Δx \\ Δ ε_{z} & 1 & - Δ ε_{x} & Δy \\ - Δ ε_{y} & Δ ε_{x} & 1 & Δ z \\ 0 & 0 & 0 & 1 \end{matrix}] (13) \end{matrix} \end{matrix}$

式中: Δx、 Δy、 Δz为刀具实际切削点相对理想切削点的位置误差; Δε_x、 Δε_y、 Δε_z为刀具实际切削点相对理想切削点的方向误差。

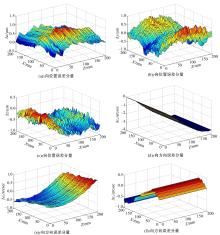
综上所述,基于小误差假设并忽略二阶及二阶以上小量,可得到四轴抛光平台综合误差空间分量:

$\begin{matrix} \begin{matrix} Δx = \cos θ_{C} δ_{x θ_{B}} + \cos θ_{C} δ_{xZ} - zcos θ_{C} S_{xZ} + \\ \sin θ_{C} δ_{y θ_{B}} + \sin θ_{C} δ_{yZ} - zcos θ_{C} ε_{yX} + zsin θ_{C} ε_{xX} - \\ z ε_{y θ_{C}} - \cos θ_{C} δ_{x θ_{C}} + xsin θ_{C} ε_{z θ_{C}} + xsin θ_{C} ε_{z θ_{C}} - \\ \cos θ_{C} δ_{xX} - \sin θ_{C} δ_{y θ_{C}} - \sin θ_{C} δ_{yX} (14) \\ Δy = - \sin θ_{C} δ_{x θ_{B}} - \sin θ_{C} δ_{xZ} + zsin θ_{C} δ_{xZ} + \\ \cos θ_{C} δ_{y θ_{B}} + \cos θ_{C} δ_{yZ} + zsin θ_{C} ε_{yX} + zcos θ_{C} ε_{xX} - \\ z ε_{x θ_{C}} + \sin θ_{C} δ_{x θ_{C}} + \sin θ_{C} δ_{xx} + xcos θ_{C} ε_{xZ} - \\ \cos θ_{C} δ_{y θ_{C}} + xcos θ_{C} ε_{z θ_{C}} - \cos θ_{C} δ_{yX} (15) \\ Δz = δ_{z θ_{B}} + δ_{zZ} - xcos θ_{C} ε_{y θ_{C}} - xsin θ_{C} ε_{x θ_{C}} - \\ x ε_{yx} + δ_{x θ_{C}} + δ_{zX} (16) \\ Δ ε_{x} = \sin θ_{C} ε_{y θ_{C}} - \cos θ_{C} ε_{x θ_{C}} - ε_{xX} + ε_{xZ} + \\ \sin θ_{B} ε_{z θ_{B}} + \cos θ_{B} ε_{y θ_{B}} (17) \\ Δ ε_{y} = \cos θ_{B} \cos θ_{C} ε_{y θ_{B}} - \sin θ_{B} \sin θ_{C} ε_{z θ_{C}} - \\ \sin θ_{B} \sin θ_{C} ε_{zX} + \cos θ_{B} \cos θ_{C} ε_{yZ} + \\ \sin θ_{B} \cos θ_{C} ε_{zZ} - \sin θ_{C} ε_{x θ_{B}} - \cos θ_{B} \sin θ_{C} ε_{xZ} - \\ \cos θ_{B} \cos θ_{C} ε_{yX} + \cos θ_{B} \sin θ_{C} ε_{xX} - \cos θ_{B} ε_{y θ_{C}} (18) \\ Δ ε_{z} = - \cos θ_{B} \cos θ_{C} ε_{z θ_{C}} - \cos θ_{B} \cos θ_{C} ε_{zX} + \\ \sin θ_{B} \sin θ_{C} ε_{y θ_{B}} + \sin θ_{B} \sin θ_{C} ε_{yZ} + \\ \cos θ_{B} \cos θ_{C} ε_{zZ} + \cos θ_{C} ε_{z θ_{B}} + \sin θ_{B} \cos θ_{C} ε_{x Z} - \\ \sin θ_{B} \sin θ_{C} ε_{yX} - \sin θ_{B} \cos θ_{C} ε_{xX} + \sin θ_{B} ε_{x θ_{C}} (19) \end{matrix} \end{matrix}$

当两个旋转轴不动,即 θ_B=0和 θ_C=0,由式(14) ~式(19)可得 X轴和 Z轴联动工况下各轴的位置误差和方向误差分量为:

$\begin{matrix} \{\begin{matrix} Δx = δ_{xZ} - z ε_{yX} - z S_{xZ} - δ_{xX} \\ Δy = δ_{yZ} + z ε_{xX} + x ε_{zX} - δ_{yX} \\ Δz = δ_{zZ} - x ε_{yX} + δ_{zX} \\ Δ ε_{x} = - ε_{xX} + ε_{xZ} \\ Δ ε_{y} = ε_{yZ} - ε_{yX} \\ Δ ε_{z} = - ε_{zX} + ε_{zZ} \end{matrix} \end{matrix}$

当 C轴不动( θ_C=0), B轴转动 θ_B角时,由式(14) ~式(19)可得 B轴、 X轴和 Z轴联动工况下各轴的位置误差和方向误差分量为:

$\begin{matrix} \{\begin{matrix} Δx = \cos θ_{B} δ_{x θ_{B}} + \sin θ_{B} δ_{z θ_{B}} + δ_{xZ} - z ε_{yX} - \\ z S_{xZ} - δ_{xX} \\ Δy = δ_{y θ_{B}} + δ_{yZ} + z ε_{xX} + x ε_{xZ} - δ_{yX} \\ Δz = - \sin θ_{B} δ_{x θ_{B}} + c os θ_{B} δ_{z θ_{B}} + δ_{zZ} - x ε_{yX} + δ_{zX} \\ Δ ε_{x} = - ε_{xX} + ε_{xZ} + \sin θ_{B} ε_{z θ_{B}} + \cos θ_{B} ε_{y θ_{B}} \\ Δ ε_{y} = \cos θ_{B} ε_{y θ_{B}} + \cos θ_{B} ε_{yZ} + \sin θ_{B} ε_{zZ} - \\ \sin θ_{C} ε_{x θ_{B}} - \cos θ_{B} ε_{yZ} \\ Δ ε_{z} = - \cos θ_{B} ε_{zX} + \cos θ_{B} ε_{zZ} + ε_{z θ_{B}} + \\ \sin θ_{B} ε_{xZ} - \sin θ_{B} ε_{xX} \end{matrix} \end{matrix}$

2 单项误差测量和综合误差分析

2.1 各轴单项误差测量试验条件

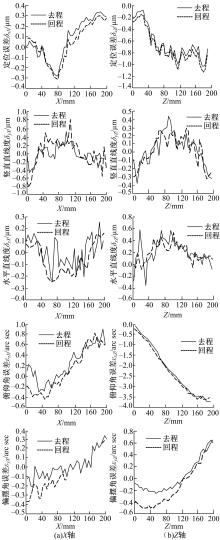
针对抛光平台 X轴和 Z轴的定位误差、水平直线度、竖直直线度、俯仰角误差和偏摆角误差以及 B轴转台的角度定位误差,利用雷尼绍(Renishaw)公司的XL-80激光干涉仪系统进行测量。其余单项误差源均假设为零。

2.2 各轴单项测量结果分析

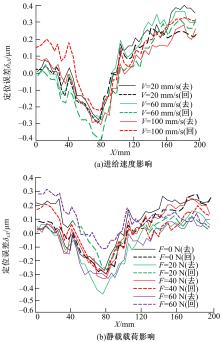
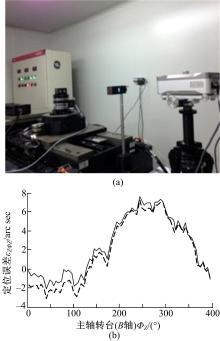
测量数据处理按ISO 230-2标准进行。图3为在不同速度和不同载荷情况下 X轴定位误差测量结果。结果表明,不同载荷和速度对 X轴定位误差没有显著影响。将其测量结果同文献[16]的滚珠丝杠驱动运动平台的定位误差进行比较,发现气浮平台定位误差没有明显的线性增加或减小的趋势。这是由于滚珠丝杠螺距误差的累积导致其定位误差具有明显的线性增长或减小趋势,而影响气浮平台定位误差的主要因素是直线电机特性和导轨面几何误差。图4为 B轴转台定位误差测量现场及测量结果。

	Figure Option View Download New Window
	图3 不同载荷与速度下 X轴定位误差Fig.3 Positioning error of X-axis under different loads and speeds

	Figure Option View Download New Window
	图4 B轴转台定位误差Fig.4 Positioning error of B-axis rotary table

图5为 X轴和 Z轴的各单项几何误差测量结果。由图5不难看出,竖直直线度大于定位误差和水平直线度,而文献[16]中滚珠丝杠驱动运动平台的竖直直线度要明显小于定位误差。所以对于采用气浮平台的超精密测量和加工设备,竖直直线度是一个不可忽视的误差源。

	Figure Option View Download New Window
	图5 X轴和 Z轴几何误差Fig.5 Geometric errors of X and Z axes

由图6(a)可得到 Z轴斜度为-663.4180 μm/m;由图6(b)可得到 X轴斜度为748.1532 μm/m,从而得到垂直度误差为 S_XY=-103.6429 μm/m。

	Figure Option View Download New Window
	图6 X轴和 Z轴垂直度误差Fig.6 Squareness errors between X and Y-axes

2.3 抛光平台综合误差分析

将试验测得的各单项几何误差数据代入综合误差模型,得到如图7所示的 X轴和 Z轴联动工况下,综合误差在 x、 y、 z向的位置误差分量和方向误差分量。 X轴和 Z轴的运动范围为0~200 mm。从图7中可以看出: y向位置误差分量为-1~1 μm,明显大于 x向和 z向的位置误差分量。 x向方向误差分量远大于 y、 z向方向误差分量,分析其原因是抛光平台 Z轴存在很大的俯仰角。

	Figure Option View Download New Window
	图7 四轴抛光平台综合误差分析Fig.7 Components of the volumetric error for four-axis polishing platform

4 结束语

利用多体系统理论建立了由两个直线电机驱动的气浮平台和两个旋转台组成的四轴抛光平台的综合误差模型。针对四轴抛光平台移动轴和旋转轴存在耦合的情况,通过定量分析确定了影响综合误差的显著因素。应用激光干涉仪对四轴抛光平台各轴的定位误差、直线度、俯仰角和偏摆角等几何误差进行反复测量,将测量结果代入综合误差模型获得综合误差在 x、 y、 z向的位置误差分量和方向误差分量的变化规律,为通过软件补偿提高抛光加工精度奠定了理论基础。将直线电机驱动的气浮平台的几何误差测量结果与滚珠丝杠驱动平台的几何误差进行对比分析,发现直线电机驱动的气浮平台的竖直方向直线度是不可忽略的误差因素。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	杨建国. 数控机床误差补偿技术现状与展望[J]. 航空制造技术, 2012(5): 40-45. Yang Jian-guo. Present situation and prospect of error compensation technology for NC machine tool[J]. Aeronautical Manufacturing Technology, 2012(5): 40-45. [本文引用:1] [CJCR: 0.3783]
[2]	王维, 杨建国, 姚晓栋, 等. 数控机床几何误差与热误差综合建模及其实时补偿[J]. 机械工程学报, 2012, 48(7): 165-170. Wang Wei, Yang Jian-guo, Yao Xiao-dong, et al. Synthesis modeling and real-time compensation of geometric error and thermal error for CNC machine tools[J]. Journal of Mechanical Engineering, 2012, 48(7): 165-170. [本文引用:1] [CJCR: 0.544]
[3]	王秀山, 杨建国, 闫嘉钰. 基于多体系统理论的五轴机床综合误差建模技术[J]. 上海交通大学学报, 2008, 42(5): 761-764. Wang Xiu-shan, Yang Jian-guo, Yan Jia-yu. Synthesis error modeling of the five axis machine tools based on multi-body system theory[J]. Journal of Shanghai Jiaotong University, 2008, 42(5): 761-764. [本文引用:1]
[4]	Lee R S, Lin Y H. Applying bidirectional kinematics to assembly error analysis for five-axis machine tools with general orthogonal configuration[J]. International Journal of Advanced Manufacturing Technology, 2012, 62(9-11): 1261-1272. [本文引用:1] [JCR: 1.205]
[5]	Zhang Yi, Yang Jian-guo, Zhang Kun. Geometric error measurement and compensation for the rotary table of five-axis machine tool with double ballbar[J]. International Journal of Advanced Manufacturing Technology, 2013, 65(1-4): 275-281. [本文引用:1] [JCR: 1.205]
[6]	范晋伟, 宋贝贝, 王称心, 等. TTTRR型五轴数控机床通用几何误差补偿关键技术的研究[J]. 机械设计与制造, 2012(5): 171-173. Fan Jin-wei, Song Bei-bei, Wang Chen-xin, et al. Research on key technology of general geometric error compensation of “TTTRR” type 5-axis numerical control machine[J]. Machinery Design & Manufacture, 2012(5): 171-173. [本文引用:1]
[7]	Kong L B, Cheung C F, To S, et al. A kinematics and experimental analysis of form error compensation in ultra-precision machining[J]. International Journal of Machine Tools and Manufacture, 2008, 48(12-13): 1408-1419. [本文引用:1] [JCR: 2.262]
[8]	刘志峰, 刘广博, 程强, 等. 基于多体系统理论的精密立式加工中心精度建模与预测[J]. 吉林大学学报: 工学版, 2012, 42(2): 388-391. Liu Zhi-feng, Liu Guang-bo, Cheng Qiang, et al. Precision modeling and prediction of precise vertical machining center based on theory of multi-body system[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(2): 388-391. [本文引用:1] [CJCR: 0.701]
[9]	粟时平, 李圣怡. 五轴数控机床综合空间误差的多体系统运动学建模[J]. 组合机床与自动化加工技术, 2003(5): 15-18. Su Shi-ping, Li Sheng-yi. Modeling the volumetric synthesis error of 5-axis machine tools based on multi-body system kinematics[J]. Modular Machine Tools and Automatic Manufacturing Technique, 2003(5): 15-18. [本文引用:1]
[10]	Chow J H, Zhong Z W, Lin W, et al. A study of thermal deformation in the carriage of a permanent magnet direct drive linear motor stage[J]. Applied Thermal Engineering, 2012, 48: 89-96. [本文引用:1] [JCR: 2.127]
[11]	Gao W, Arai Y, Shibuya A, et al. Measurement of multi-degree-of-freedom error motions of a precision linear air-bearing stage[J]. Precision Engineering, 2006, 30(1): 96-103. [本文引用:1] [JCR: 1.393]
[12]	Ekinci T O, Mayer J R R. Relationships between straightness and angular kinematic errors in machines[J]. International Journal of Machine Tools and Manufacture, 2007, 47(12-13): 1997-2004. [本文引用:1] [JCR: 2.262]
[13]	Onat E T, Mayer J R R, Cloutier G M. Investigation of accuracy of aerostatic guideways[J]. International Journal of Machine Tools and Manufacture, 2009, 49(6): 478-487. [本文引用:1] [JCR: 2.262]
[14]	Mu Dong-hui, Chen Dong-ju, Fan Jin-wei, et al. Carriage error identification based on cross-correlation analysis and wavelet transformation[J]. Sensors, 2012, 12: 9551-9565. [本文引用:1] [JCR: 1.953]
[15]	杨建国, 范开国, 杜正春, 等. 数控机床误差实时补偿技术[M]. 北京: 机械工业出版社, 2013. [本文引用:1]
[16]	韩飞飞, 赵继, 张雷, 等. 数控机床几何精度综合解析与试验研究[J]. 机械工程学报, 2012, 48(21): 141-148. Han Fei-fei, Zhao Ji, Zhang Lei, et al. Synthetical analysis and experimental study of the geometric accuracy of CNC machine tools[J]. Journal of Mechanical Engineering, 2012, 48(21): 141-148. [本文引用:1] [CJCR: 0.544]

0.0

0.3783

2012

0.0

0.544

2008

0.0

. 2008, 42(5):761-764

Synthesis error modeling of the five axis machine tools based on multi-body system theory

采用多体系统理论完成了五轴数控机床的综合误差建模,对平动轴间垂直度误差做了建模分析,改进了热误差的建模和辨识.该方法简便、明确,不受机床结构和运动复杂程度的限制,为计算机床误差、实现误差实时补偿、修正控制指令和提高加工精度提供了理论基础.

2012

1.205

0.0

. 2012, 62(9-11):1261-1272 DOI:10.1007/s00170-011-3860-y

Applying bidirectional kinematics to assembly error analysis for five-axis machine tools with general orthogonal configuration

<li>1.National Cheng Kung University, Tainan, Taiwan, Republic of China</li>

Abstract
Since a five-axis machine tool has two more rotary axes and two more degrees of freedom than a three-axis machine tool, it can manufacture a complex surface more efficiently. However, there are more error terms due to the extra axes. Error sources for machine tools include structural error, dynamic error, and static error. The static error, which includes thermal and geometric errors, is the main source of machining inaccuracy in machine tools. Although a large number of studies have been made on geometric errors, the influence of individual error term on volumetric error is seldom discussed. This paper analyzes assembly error that belongs to the category of static error, and the analytic method can be applied to general orthogonal configurations. By adopting the machine tool form-shaping function, the effect of assembly errors on volumetric errors has been investigated. And the error terms that cannot be compensated by driving single control axis have been recognized and explored for general orthogonal configurations.

2013

1.205

0.0

. 2013, 65(1-4):275-281 DOI:10.1007/s00170-012-4166-4

Geometric error measurement and compensation for the rotary table of five-axis machine tool with double ballbar

<li>1.School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China</li>

Abstract

This paper proposes a novel measuring method for geometric error identification of the rotary table on five-axis machine tools by using double ballbar (DBB) as the measuring instrument. This measuring method greatly simplifies the measurement setup, for only a DBB system and a height-adjustable fixture are needed to evaluate simultaneously five errors including one axial error, two radial errors, and two tilt errors caused by the rotary table. Two DBB-measuring paths are designed in different horizontal planes so as to decouple the linear and angular errors. The theoretical measuring patterns caused by different errors are simulated on the basis of the error model. Finally, the proposed method is applied to a vertical five-axis machining center for error measurement and compensation. The experimental results show that this measuring method is quite convenient and effective to identify geometric errors caused by the rotary table on five-axis machine tools.

0.0

2008

2.262

0.0

. 2008, 48(12-13):null-null

A kinematics and experimental analysis of form error compensation in ultra-precision machining

2012

0.0

0.701

. 2012, 42(2):388-391

Precision modeling and prediction of precise vertical machining center based on theory of multi-body system

College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, China

In order to predict the machining precision of the machine tool and validate its design concept, the geometric errors of a precise vertical machining center were analyzed, and its precision prediction model was established based on the multi-body system theory. The correlations among the multi-bodies were described with the topology structure and the low-order body array. The coordinate transformation relationships between multi-bodies were described based on the homogeneous transformation matrix. The characteristic matrix and the relative motion equations of the motions between 2 arbitrary adjacent objects of the multi-body system were derived. A precision prediction model was built for the precise vertical machining center. Based on the simulated machining of a typical workpiece, the precision prediction of the machine tool was realized. The results showed that the proposed precision model can describe the systemic structure of the vertical machining center effectively and abstractively, predict the machining precision reasonably, provide a basis for the improvement of the machine tool design concept and the precision deployment.

为了对机床加工精度进行事先预测并验证设计方案的合理性,分析了几何误差因素,基于多体系统理论建立了精密立式加工中心的精度预测模型。用拓扑结构和低序体阵列描述了多体系统间的关联性。基于齐次变换矩阵描述体与体之间的坐标变换关系,推导出多体系统中任意两相邻体之间各种运动的特征矩阵和相对运动方程,最终建立了精密立式加工中心精度预测模型,并以模拟加工典型试件为基础,实现了对机床的精度预测。预测分析表明,基于多体系统的精度建模可以有效抽象地描述精密立式加工中心的系统结构,并实现加工精度的合理预测,为机床设计方案的改进及精度分配提供了重要的依据。

0.0

. , 2003(5):15-18

Modeling the volumetric synthesis error of 5-axis machine tools based on multi-body system kinematics

基于多体系统运动学理论的基本原理,结合RRTTT型五轴立式数控机床,阐述了多体系统的拓扑结构和低序体阵列,提出了特征矩阵的基本概念和构建方法,分析了多体系统有误差运动的基本规律,研究了根据特征矩阵得到综合空间误差的算法.理论分析和实例建模都显示所述方法能很好地解决误差建模的正确性、速度、通用性和自动化问题,为五轴数控机床精度分析和误差补偿提供了一种理想的误差建模技术.

2012

2.127

0.0

. 2012, 48:null-null

A study of thermal deformation in the carriage of a permanent magnet direct drive linear motor stage

... 直线电机驱动气浮平台的传动方式越来越多地应用在半导体制造设备、超精密机床和测量仪器上,气浮平台自身的运动误差直接影响系统的性能,最终影响加工和测量精度^[10] ...

2006

1.393

0.0

. 2006, 30(1):null-null

Measurement of multi-degree-of-freedom error motions of a precision linear air-bearing stage

2007

2.262

0.0

. 2007, 47(12-13):null-null

Relationships between straightness and angular kinematic errors in machines

2009

2.262

0.0

. 2009, 49(6):478-487 DOI:10.1016/j.ijmachtools.2009.01.001

Investigation of accuracy of aerostatic guideways

Abstract

Aerostatic guideways are often used in machines requiring very high motion accuracy such as coordinate measuring machines. Currently, positioning error analysis for such machines focuses on the relationship between volumetric errors on one hand and axes’ motion errors and axes’ relative location errors on the other. The internal mechanisms causing motion errors are rarely considered. In order to gain a deeper understanding of aerostatic guideways, this paper investigates the relationship between the motion errors of the axis’ carriage and the guideways’ geometric errors both mathematically and experimentally. The analytical model uses bearings location and stiffness, guideway geometry and static equilibrium to produce a model in matrix form. Validation experiments are conducted on a machine axis moving on aerostatic guideways with and without preload.

2012

1.953

0.0

2013

0.0

... (3)基于小误差假设,工件坐标系3到刀具坐标系7的综合误差变换矩阵为^[15]: ...

2012

0.0

0.544