多孔仿生射流表面减阻特性数值模拟

引用本文

李芳, 赵刚, 刘维新, 孙壮志. 多孔仿生射流表面减阻特性数值模拟. 44(6): 1698-1703
LI Fang, ZHAO Gang, LIU Wei-xin, SUN Zhuang-zhi. Numerical simulation of drag reduction characteristics of a bionic jet surface with multiple holes. Journal of Jilin University Engineering and Technology Edition, 44(6): 1698-1703 复制到剪切板

Permissions

多孔仿生射流表面减阻特性数值模拟

李芳, 赵刚, 刘维新, 孙壮志

哈尔滨工程大学机电工程学院,哈尔滨 150001

作者简介:李芳(1985-),女,博士研究生.研究方向:仿生射流减阻技术.E-mail:lifang71118@163.com

基金:国家自然科学基金项目(51275102);

摘要

利用RNGk-ε湍流模型对流体在多孔仿生射流表面上的流动特性进行了数值模拟。结果表明:减阻率和流速比呈线性关系,流速比越大减阻效果越好,最大减阻率为59.02%;单孔射流表面中心线上的摩擦阻力系数先减小后增大,局部减阻率最大为111.8%;射流孔越多,减阻效果越好。探讨了仿生射流表面减阻机理:射流通过改变其表面附近的流场结构,使得边界层黏性底层的厚度增加,垂直于壁面的法向速度梯度减小,达到了显著的减阻效果;同时产生稳定的流向涡结构,并在壁面处形成小的二次涡,抑制了流体间的动量交换,减小了摩擦阻力。

关键词: 工程仿生学; 仿生射流表面; 数值模拟; 减阻; 边界层

中图分类号:TB17 文献标志码:A 文章编号:1671-5497(2014)06-1698-06

Numerical simulation of drag reduction characteristics of a bionic jet surface with multiple holes

LI Fang, ZHAO Gang, LIU Wei-xin, SUN Zhuang-zhi

College of Mechanical and Electrical Engineering,Harbin Engineering University, Harbin 150001, China

Abstract

Numerical simulation is carried out to study the drag reduction characteristics of porous bionic jet surface according to RNGk-ε turbulence model. The results show that there exists a linear dependency of the drag reduction on the rate of velocity, that is, the higher the rate of the velocity, the better the effect of drag reduction. The maximal efficiency of drag reduction is 59.02%. Friction coefficient decreases at first, and then increases along with the central line of the bionic jet surface with single hole. The efficiency of drag reduction in local region can be up to 111.8%. Furthermore, the more the number of jet holes, the better the drag reduction effect. The mechanism of the drag reduction of the bionic jet surface is studied. It is found that the jet-flow increases the thickness of the viscous sublayer in the boundary layer by changing the structure of the flow field in the vicinity of the jet surface. As a result, the gradient of normal velocity, perpendicular to the surface, is decreased, which contributes to remarkable drag reduction. Meanwhile, the gradient of normal velocity generates streamwise vortex structure and develops small secondary vortex on the surface, which results in inhibiting momentum exchange between fluids, thus, reducing the friction on the jet surface.

Keyword: engineering bionics; bionic jet surface; numerical simulation; drag reduction; boundary layer

Show Figures

仿生学家发现鲨鱼表皮沿流向排列的V型微沟槽结构是有利于其射流减阻的体表形态^{[ 1]},受此启发,国内外学者对微沟槽结构^{[ 2, 3, 4]}、凹坑和凸包等结构^{[ 5, 6]}进行了大量研究,但针对射流表面减阻技术的研究相对较少,且主要集中在超声速飞行器表面减阻领域^{[ 7]}。尽管射流表面减阻技术在超声速航行体表面取得了较好的效果,但水下环境更为复杂,在航空领域得到的射流减阻特性是否适用于水下环境有待进一步研究。另外,前期对仿生射流减阻技术的研究都是基于单孔射流^{[ 8]},而多孔射流表面的流场结构与单孔相比具有较大的不同,多孔射流表面是否能够减阻以及减阻特性如何也有待进一步研究。因此,本文建立了类似鲨鱼鳃部结构的多孔射流表面模型,并对流体在其表面的流动特性进行了数值模拟,研究流速比和射流孔个数对减阻效果的影响规律,分析矩形多孔射流表面的减阻机理。

1 计算域的建立和离散化

1.1 仿生射流表面模型的建立

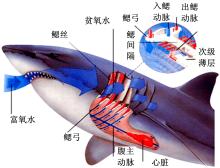
本文的仿生对象为白斑星鲨,俗称白点鲨、星鲨、鲨皮,软骨鱼纲、真鲨目、皱唇鲨科、星鲨属。体长701.5 mm,头长170.5 mm,头部两侧共有5对鳃裂,鳃裂长度12.5~20 mm,鳃裂宽度1.5~5 mm,鳃间隔5.5~10 mm。鲨鱼在游动的过程中,富氧水进入口咽腔,经鳃部进行气体交换后,贫氧水从鳃裂部位流出形成射流,如图1所示。

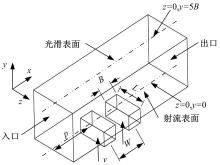
	Figure Option View Download New Window
	图1 鲨鱼鳃部的呼吸射流过程Fig.1 Breathing and jet process of Shark gills

分布于鲨鱼头部两侧的鳃裂相对于第一背鳍具有对称性,现以一侧鳃裂为例,将鳃裂周围鲨鱼的体表结构简化为平板,鳃裂简化为分布在平板上游的射流孔,将鳃裂部位喷水的过程简化为连续的射流过程,通过射流孔向主流场中进行连续射流以改变射流表面附近的流场结构。为评价仿鲨鱼鳃部射流表面模型的减阻效果,将上表面作为对照表面,通过对比相同流场条件下光滑表面和开有射流孔的射流表面的摩擦阻力来评价其减阻效果。根据白斑星鲨头部一侧的鳃裂数,建立了五孔射流表面模型,研究发现相邻两个射流孔的流体存在相互作用,为研究这种相互作用对减阻效果的影响,以最简单的双孔射流为例进行研究,再将多孔射流与单孔射流进行对比,以研究多孔射流和单孔射流之间的关系,建立仿生射流表面模型如图2所示。

	Figure Option View Download New Window
	图2 仿生射流表面模型Fig.2 Model for bionic jet surface

图2为双孔射流表面模型计算域示意图,单孔模型为只有第一个射流孔的情况,五孔模型则依次排列5个射流孔。射流孔宽度 B=2 mm,本文中尺寸均与射流孔宽度 B对比进行量纲归一化处理。 x、 y、 z分别为流向、法向和展向方向,计算域长、宽、高比值为7 ∶2 ∶1;第一个射流孔的中心位置位于坐标原点,其入口距离 p=-5 B、距两侧壁等距离,射流孔长度 L=7 .5 B,射流角度为90 °,与主流速度方向垂直;相邻两个射流孔中心间距 W=4 B,射流孔中心分别位于 x/B=0、4、8、12、16处;各个模型的射流孔参数相同;主流方向速度为 V,射流速度为 v。

1.2 网格划分

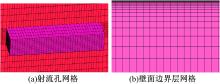
利用ICEM CFD14.0对计算域进行结构化网格划分,对于单孔射流表面模型在主流速度为10 m/s时进行计算域网格划分,将网格节点数从24.5万加密到42.7万时计算误差在0.5%以内,达到了计算精度的要求。全局网格尺寸参数设置为0.8 mm,在射流表面和光滑表面进行网格加密处理,壁面第一层网格的高度为0.002 mm,网格增长率为1.1,在主流速度为10 m/s时满足 y⁺=1。 y⁺为第一层网格到壁面的无量纲距离。本文所建立模型的网格节点总数在(24.5~32.5)万之间,网格划分情况如图3所示。

	Figure Option View Download New Window
	图3 仿生射流表面网格划分示意图Fig.3 Sketch map of bionic jet surface meshes

1.3 湍流模型

标准 k-ε模型是一种高雷诺数的模型,而RNG k-ε模型提供了一个考虑低雷诺数流动黏性的解析公式,使得RNG k-ε模型比标准 k-ε模型具有更高的可信度和精度。由于需要研究近壁面流体的流动情况,所以本文选用RNG k-ε模型和增强型壁面函数。

$\begin{matrix} \begin{matrix} \frac{\partial (ρk)}{\partial t} + \frac{\partial (ρ u_{i} k)}{\partial x_{i}} = - \frac{\partial}{\partial x_{j}} (μ_{0} + \frac{μ_{t}}{σ_{k}}) \frac{\partial k}{\partial x_{j}} + p_{k} - ρε (1) \\ \frac{\partial (ρε)}{\partial t} + \frac{\partial (ρ u_{i} ε)}{\partial x_{i}} = \frac{\partial}{\partial x_{j}} (μ_{0} + \frac{μ_{t}}{σ_{ε}}) \frac{\partial ε}{\partial x_{j}} + \\ C_{ε 1} p_{k} \frac{ε}{k} - C_{ε 2} ρ \frac{ε^{2}}{k} - R_{ε} (2) \end{matrix} \end{matrix}$

式中: ρ为流体密度; k为湍流运动能量; ε为湍流耗散系数;漩涡 μ_t=ρC_μk² /ε;湍动能产生项 p_k=μ_tS², S= $\begin{matrix} \sqrt[]{2 S i_{j} S_{ij}} \end{matrix}$ , S_ij=1 /2( ∂u_i/∂x_j+∂u_i/∂x_i);控制项 R_ε=C_μρη³(1 -η/η₀) ε² /[ k(1 +βη³)], η=Sk/ε;常系数 σ_k=1 .39; σ_ε=1 .39; C_ε₁ =1 .42; C_ε₂ =1 .68; C_μ=0 .084; η₀ =4 .38; β=0 .012。

1.4 边界条件和求解方法

求解方法选择基于压力求解器中的SIMPLEC算法,离散格式选择二阶迎风格式。计算域主流场分别采用速度入口和压力出口边界条件,射流孔入口采用速度入口边界条件,光滑表面和射流表面均为无滑移绝热壁面;选用水作为流体介质,主流孔入口速度分别为10、15和20 m/s,射流孔入口速度分别为0.6、1、1.5、2、2.5、3、4、4.5、6 m/s;能量方程的残差设为1×10^-6,其余方程残差均设为1×10^-4。

2 数值模拟结果

流体流过固体表面时,所受到的阻力包括摩擦阻力和压差阻力两部分,其中压差阻力属于形状阻力,光滑表面和射流表面均与流场方向平行,因此本文忽略压差阻力,只考虑摩擦阻力。模型表面的摩擦阻力包括 x、 y、 z三个方向的力,但是相对于 x方向而言,其余两个方向的分力可以忽略不计,文中所指的摩擦阻力为 x方向分力。

2.1 减阻效果评价

减阻率为:

$\begin{matrix} R = \frac{C_{fs} - C_{fj}}{C_{fs}} \times 100 % (3) \end{matrix}$

式中: R为减阻率; C_fs为光滑表面摩擦阻力系数; C_fj为射流表面摩擦阻力系数。

流速比 R_v为:

$\begin{matrix} R_{v} = v / V (4) \end{matrix}$

射流流量为:

$\begin{matrix} Q = Av (5) \end{matrix}$

式中: A为单个射流孔面积。

2.2 摩擦阻力特性分析

2.2.1 流速比对减阻效果的影响

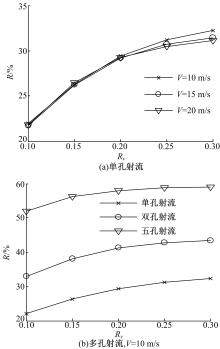
流速比对减阻效果的影响规律如图4所示。图4(a)为单孔射流表面模型主流速度变化时的减阻率曲线。分析图4(a)可知,同时改变主流速度和射流速度使之保持流速比不变,减阻率几乎保持不变,说明流速比是影响射流流场的主要因素^{[ 9]};减阻率与流速比呈线性关系,随着流速比的增大,减阻率逐渐增大。分析图4(b)可知,射流孔个数越多减阻效果越好,最大减阻率为59.02%。单孔、双孔和五孔射流的减阻率与流速比呈近似线性关系,即当主流速度不变时,射流速度越大减阻效果越好^{[ 10]}。

	Figure Option View Download New Window
	图4 仿生射流表面减阻率曲线Fig.4 Drag reduction ratio of bionic jet surface

2.2.2 射流孔个数对减阻效果的影响

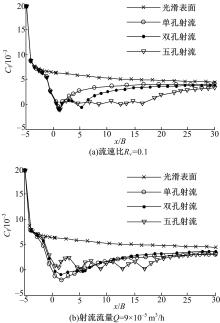
图5为单孔、双孔和五孔射流表面模型光滑表面和射流表面中心线上的摩擦阻力系数(光滑表面中心线: z=0、 y=5 B;射流表面中心线 z=0、 y=0)。图5(a)为流速比固定不变时具有不同射流孔个数的射流表面和光滑表面的摩擦阻力系数曲线。分析图5(a)可知,当 x/B>-2时,射流表面的摩擦阻力系数小于光滑表面的摩擦阻力系数,实现了减阻。射流表面的摩擦阻力系数 C_f与 x/B呈波浪形,波谷位于射流孔下游,波谷的个数与射流孔的个数相等,即在射流孔附近出现局部的最小值点,距离射流孔越远,摩擦阻力系数越大,但始终低于光滑表面的摩擦阻力系数。在第一个射流孔的背流面摩擦阻力系数最小,局部减阻率达111.8%。

	Figure Option View Download New Window
	图5 光滑表面和射流表面中心线上的摩擦阻力系数Fig.5 Variation of C_f with x/B in the center line of smooth and jet surface

根据普朗特公式得到光滑表面平板的摩擦阻力系数为5.014×10^-3,见式(6)。由图5可知,本文光滑表面的平均摩擦阻力系数为5.002×10^-3,相对误差为0.24%,证明了本文数值模拟结果的准确性。

$\begin{matrix} C_{f} = 0.074 R e_{L_{x}}^{- 1 / 5} = 0.074 {(\frac{V L_{x}}{ν})}^{- \frac{1}{5}} (6) \end{matrix}$

式中: $\begin{matrix} R e_{L_{x}} \end{matrix}$ 为基于流场长度的雷诺数; L_x为光滑表面沿流向的长度;本文取 L_x=70 mm; V=10 m/s; ν=1.0×10^-6 m²/s。

分析图5(a)可知,当流速比固定不变时,射流孔个数越多,射流表面的平均摩擦阻力系数越小,减阻效果越好。其原因是:沿流向排布的射流孔个数越多,射流流量越大,射流流体沿流向作用的区域越大,减阻效果越好。单孔射流和双孔射流在第一个射流孔的迎流面和背流面均出现逆流区,五孔射流只在第一个射流孔附近出现逆流区。其原因是:第一个射流孔对主流产生遮挡作用,使两个射流孔之间的流体速度低于主流速度,使其与射流流体的相互作用减弱。

图5(b)为射流流量固定不变时光滑表面和多孔射流表面中心线上的摩擦阻力系数沿 x方向的变化曲线。当单孔射流 R_v=0 .3、双孔射流 R_v=0 .15、五孔射流 R_v=0 .06时,单孔、双孔、五孔射流表面模型的射流流量均为9×10^-5 m³/h。分析图5(b)可知,单孔、双孔、五孔射流表面中心线上的摩擦阻力系数均低于光滑表面;五孔射流表面的平均摩擦阻力系数最小,双孔其次,单孔最大。射流流量固定不变时,射流孔个数越多减阻效果越好。其原因是:多孔射流相对于单孔射流而言射流速度减小,消耗的湍动能减小,湍流雷诺应力减小,继而减小了射流表面的摩擦阻力。

综上所述,射流孔个数越多,射流表面的减阻效果越好。多孔射流的减阻效果优于单孔射流,但是小于多个单孔射流的减阻率之和。原因是:在本文所建立的模型中第一个射流孔的射流流体对其下游的全部区域产生影响,而其他射流孔的射流影响射流表面的区域减小了;相邻两个射流孔的射流流体存在相互作用,消耗了更多的湍动能;第一个射流孔的射流流体对主流的阻碍作用最为明显,其余射流孔的射流流体对主流的遮挡作用减弱,射流孔下游局部摩擦阻力系数降低的幅度减小。

3 仿生射流表面减阻机理

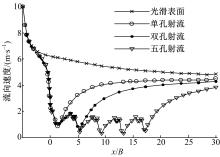
当 R_v=0 .1时,光滑表面和射流表面模型中底面附近 x/B=-5 ~30, y/B=0 .015, z/B=0( δ⁺≈0 .08, δ⁺为监测点至壁面的距离与边界层厚度 δ的比值)直线上主流方向速度大小如图6所示。分析图6可知,射流表面边界层内流向速度由于射流的遮挡作用呈现出锯齿形,射流表面附近的平均流向速度小于光滑表面,说明由于射流的存在使得射流表面边界层内的流速降低,其作用相当于增加边界层的厚度。

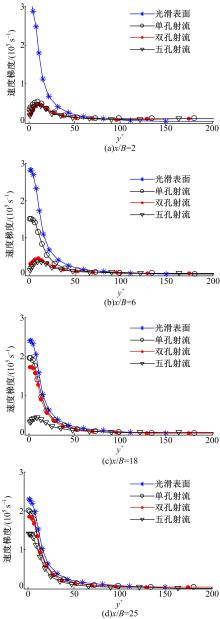
	Figure Option View Download New Window
	图6 射流表面与光滑表面近壁面区域速度对比Fig.6 Comparison of x-velocities near wall between the jet

由于射流流体的作用也会对主流方向速度产生影响,在垂直于射流表面法线方向上的不同位置取主流方向速度,并与相应位置的光滑表面速度进行对比。所取直线在射流表面的投影坐标分别为( x/B=2, z/B=0)、( x/B=6, z/B=0)、( x/B=18, z/B=0)、( x/B=25, z/B=0)。光滑表面、单孔、双孔、五孔射流表面法线方向上主流速度变化率如图7所示。分析图7可知,在靠近壁面处,射流孔附近的法向速度梯度先增大后减小,距离壁面越远,法向速度梯度越小,当 y⁺>50时光滑表面和射流表面的速度梯度均减小到最小值并保持不变;单孔、双孔、五孔射流表面附近的速度变化率均明显低于光滑表面,可以得出射流表面的壁面剪应力小于光滑表面。射流流体的存在改变了射流表面附近流体的流动情况,使得射流表面附近的法向速度梯度减小,达到了减阻效果。

	Figure Option View Download New Window
	图7 壁面法向直线上速度梯度分布Fig.7 Velocity gradient in the straight line

当单孔射流表面模型 R_v=0 .3时,垂直于主流方向( x/B=2)的法向速度云图如图8所示。分析图8可知,与光滑表面相比,射流表面由于射流流体的作用改变了法向速度,在流动方向上形成了稳定的大涡结构,并在壁面处诱导出了一些小的二次涡。二次涡抑制了流体的展向运动,从而抑制了流体间的动量交换。同时壁面附近稳定的流向涡和二次涡隔绝了主流高速流体对壁面的扫掠,达到减小壁面剪应力的效果。

	Figure Option View Download New Window
	图8 平面 x/B=2的法向速度云图Fig.8 Contour of y-velocity at the plane x/B=2

综上所述:射流是通过改变射流表面附近的流场的流动结构来达到减阻目的的。射流流体的存在使得壁面附近流体形成沿流向方向的锯齿形运动,增加了边界层黏性底层的厚度,使得边界层内速度梯度减小,从而减小了壁面剪应力。同时在流动方向上形成稳定的大涡结构,并在射流表面附近诱导出一些小的二次涡,阻隔了主流高速流体对壁面的扫掠,从而减小了射流表面的摩擦阻力。

4 结束语

(1)在分析鲨鱼呼吸过程的基础上,提出了仿生射流表面减阻法。利用数值模拟方法研究了单孔、双孔、五孔射流表面模型的减阻特性,结果表明:仿生射流表面的减阻率与流速比呈线性关系,减阻率随着流速比增大而增大,射流孔个数越多减阻效果越好,在不考虑射流能量的情况下,最大减阻率为59.02%。

(2)同时改变主流速度和射流速度使得流速比保持不变时,不同的主流速度具有相同的减阻率,表明流速比是影响减阻率的主要因素。

(3)射流中心对称面上的摩擦阻力系数随 x/B呈波浪形变化,在第一个射流孔下游摩擦阻力系数 C_f降低最为明显,局部减阻率达111.8%。

(4)射流改变了射流表面附近的流场结构,使得射流表面附近的边界层厚度增大,射流表面的法向速度梯度减小,继而实现了减阻效果。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Bechert D W, Bruse M, Hage W. Experiments with three-dimensional riblets as an idealized model of shark skin[J]. Experiments in Fluids, 2000, 28(5): 403-412. [本文引用:1] [JCR: 1.572]
[2]	Lee S J, Lim H C, Han M, et al. Flow control of circular cylinder with a V-grooved micro-riblet film[J]. Fluid Dynamics Research, 2005, 37(4): 246-266. [本文引用:1] [JCR: 0.758]
[3]	Lee S J, Lee S H. Flow field analysis of a turbulent boundary layer over a riblet surface[J]. Experiments in Fluid, 2001, 30(2): 153-166. [本文引用:1] [JCR: 1.572]
[4]	El-Samni O A, Chun H H, Yoon H S. Drag reduction of turbulent flow over thin rectangular riblets[J]. International Journal of Engineering Science, 2007, 45(2-8): 436-454. [本文引用:1] [JCR: 1.691]
[5]	张成春, 任露泉, 王晶. 旋成体仿生凹环表面减阻试验分析及数值模拟[J]. 吉林大学学报: 工学版, 2007, 37(1): 100-105. Zhang Cheng-chun, Ren Lu-quan, Wang Jing. Experiment and numerical simulation on drag reduction for bodies of revolution using bionic scrobiculate ringed surface[J]. Journal of Jilin University(Engineering and Technology Edition), 2007, 37(1): 100-105. [本文引用:1] [CJCR: 0.701]
[6]	谷云庆, 赵刚, 刘浩, 等. 气动灭火炮弹体橡胶圈仿生凹坑表面减阻特性[J]. 吉林大学学报: 工学版, 2013, 43(4): 983-990. Gu Yun-qing, Zhao Gang, Liu Hao, et al. Characteristics of drag reduction of bionic dimpled surface of shell rubber ring of aerodynamic extinguishing cannon[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 983-990. [本文引用:1] [CJCR: 0.701]
[7]	Endwell O D, Victor E P, Wang Ten S, et al. Dynamics of shock dispersion and interactions in supersonic freestreams with counterflowing jets[J]. AIAA Journal, 2009, 47(6): 1313-1326. [本文引用:1] [JCR: 1.08]
[8]	Zhao G, Zhao H L, Shu H S, et al. Simulation study of bionic jetting direction influence on drag reduction effect[J]. Advances in Nature Science, 2010, 3(2): 17-26. [本文引用:1]
[9]	曾玉红, 槐文信. 横流中三维圆形垂直浮力射流特性数值分析[J]. 应用基础与工程科学学报, 2005, 13(2): 120-128. Zeng Yu-hong, Huai Wen-xin. Numerical analysis for a round turbulent buoyant jet in a cross flow[J]. Journal of Basic Science and Engineering, 2005, 13(2): 120-128. [本文引用:1] [CJCR: 0.474]
[10]	谷云庆, 赵刚, 郑金兴, 等. 射流表面的主流场速度与射流速度耦合减阻特性[J]. 中南大学学报: 自然科学版, 2012, 43(12): 4713-4721. Gu Yun-qing, Zhao Gang, Zheng Jin-xing, et al. Characteristics of drag reduction on coupling of jet surface main flow field velocity and jet velocity[J]. Journal of Central South University (Science and Technology), 2012, 43(12): 4713-4721. [本文引用:1] [CJCR: 0.789]

2000

1.572

0.0

. 2000, 28(5):403-412 DOI:10.1007/s003480050400

Experiments with three-dimensional riblets as an idealized model of shark skin

1.Department of Turbulence Research Institute of Propulsion Technology German Aerospace Center (DLR) Mueller-Breslau-Strasse 8 D-10623 Berlin Germany DE DE

The skin of fast sharks exhibits a rather intriguing three-dimensional rib pattern. Therefore, the question arises whether or not such three-dimensional riblet surfaces may produce an equivalent or even higher drag reduction than straight two-dimensional riblets. Previously, the latter have been shown to reduce turbulent wall shear stress by up to 10%. Hence, the drag reduction by three-dimensional riblet surfaces is investigated experimentally. Our idealized 3D-surface consists of sharp-edged fin-shaped elements arranged in an interlocking array. The turbulent wall shear stress on this surface is measured using direct force balances. In a first attempt, wind tunnel experiments with about 365,000 tiny fin elements per test surface have been carried out. Due to the complexity of the surface manufacturing process, a comprehensive parametric study was not possible. These initial wind tunnel data, however, hinted at an appreciable drag reduction. Subsequently, in order to have a better judgement on the potential of these 3D-surfaces, oil channel experiments are carried out. In our new oil channel, the geometrical dimensions of the fins can be magnified 10 times in size as compared to the initial wind tunnel experiments, i.e., from typically 0.5 mm to 5 mm. For these latter oil channel experiments, novel test plates with variable fin configuration have been manufactured, with 1,920–4,000 fins. This enhanced variability permits measurements with a comparatively large parameter range. As a result of our measurements, it can be concluded, that 3D-riblet surfaces do indeed produce an appreciable drag reduction. We found as much as 7.3% decreased turbulent shear stress, as compared to a smooth reference plate. However, in direct comparison with 2D riblets, the performance of 3D-riblets is still inferior by about 1.7%. On the other hand, it appears conceivable, with a careful design of the fin shape (possibly supported by theory), that this inferiority in performance might be reduced. Nevertheless, at present, it seems to be rather unlikely, that 3D-riblets can significantly outperform 2D-riblets. Finally, one interesting finding remains to be mentioned: The optimum drag reduction for short 3D-riblets occurs at a lower rib height than for longer 3D-riblets or for infinitely long 2D-riblets. The same observation had been made previously on shark scales of different species with differing rib lengths, but no explanation could be given.

... 仿生学家发现鲨鱼表皮沿流向排列的V型微沟槽结构是有利于其射流减阻的体表形态^[1],受此启发,国内外学者对微沟槽结构^[2,3,4]、凹坑和凸包等结构^[5,6]进行了大量研究,但针对射流表面减阻技术的研究相对较少,且主要集中在超声速飞行器表面减阻领域^[7] ...

2005

0.758

0.0

Fluid Dyn. Res.. 2005, 37(4):246-null

Flow control of circular cylinder with a V-grooved micro-riblet film

Sang-Joon Lee 1 , Hee-Chang Lim 2,3 , Manhee Han 1 and Seung S Lee 1

<a href="mailto:hclim@soton.ac.uk" class="link" title="send mail to hclim@soton.ac.uk">hclim@soton.ac.uk</a>1Department of Mechanical Engineering, Pohang University of Science and Technology, Pohang 790-784, Korea 2School of Engineering Sciences, University of Southampton, Highfield, Southampton, SO17 1BJ, UK 3Corresponding author

Flow structure around a circular cylinder with a V-grooved micro-riblet is investigated experimentally. The results are compared with that of a smooth cylinder having the same diameter. A flexible V-shaped micro-riblet with peak-to-peak spacing of 300 μm is made using a MEMS fabrication process of PDMS (Polydimethylsiloxane) replica. The flexible micro-riblet is attached on a circular cylinder with which grooves are aligned with the streamwise flow direction. Drag force acting on the cylinder is measured for Reynolds numbers based on a cylinder diameter (D = 18 mm) in the range Re_D = 2.5 × 10³–3.8 × 10⁴. At Re_D = 3.6 × 10³ (U₀ = 3 m/s), the V-grooved micro-riblet cylinder reduces drag coefficient by 7.6%, compared with a cylinder with smooth PDMS surface. However, it increases drag coefficient about 4.2% at Re_D = 3.6 × 10⁴ (U₀ = 30 m/s). Flow field around the micro-riblet cylinder is measured by using a 2-frame PIV velocity field measurement technique. Several hundreds instantaneous velocity fields are ensemble-averaged to get the spatial distributions of turbulent statistics including turbulence intensities and turbulent kinetic energy. For the case of drag reduction at Re_D = 4.8 × 10³, the vortex formation region behind the V-grooved MRF cylinder is reduced about 10%, compared with the smooth cylinder due to enhanced entrainment of ambient inviscid fluid into the wake region. In addition, the total number of secondary vortices located inside the near wake region is decreased about 20%.

2001

1.572

0.0

. 2001, 30(2):153-166 DOI:10.1007/s003480000150

Flow field analysis of a turbulent boundary layer over a riblet surface

1.Department of Mechanical Engineering Pohang University of Science and Technology San 31 Hyoja-dong, Nam-gu, Pohang 790-784, South Korea KR

The near-wall flow structures of a turbulent boundary layer over a riblet surface with semi-circular grooves were investigated experimentally for the cases of drag decreasing (s ⁺=25.2) and drag increasing (s ⁺=40.6). One thousand instantaneous velocity fields over riblets were measured using the velocity field measurement technique and compared with those above a smooth flat plate. The field of view was 6.75 × 6.75 mm² in physical dimension, containing two grooves. Those instantaneous velocity fields were ensemble averaged to get turbulent statistics including turbulent intensities and turbulent kinetic energy. To see the global flow structure qualitatively, flow visualization was also carried out using the synchronized smoke-wire technique under the same experimental conditions. For the case of drag decreasing (s ⁺=25.2), most of the streamwise vortices stay above the riblets, interacting with the riblet tips frequently. The riblet tips impede the spanwise movement of the streamwise vortices and induce secondary vortices. The normalized rms velocity fluctuations and turbulent kinetic energy are small near the riblet surface, compared with those over a smooth flat plate. Inside the riblet valleys, these are sufficiently small that the increased wetted surface area of the riblets can be compensated. In addition, in the outer region (y ⁺ > 30), these values are almost equal to or slightly smaller than those for the smooth plate. For the case of drag increasing (s ⁺=40.6), however, most of the streamwise vortices stay inside the riblet valleys and contact directly with the riblet surface. The high-speed down-wash flow penetrating into the riblet valley interacts actively with the wetted riblet surface and increases the skin friction. The rms velocity fluctuations and turbulent kinetic energy have larger values compared with those over a smooth flat plate.

2007

1.691

0.0

. 2007, 45(2-8):null-null

Drag reduction of turbulent flow over thin rectangular riblets

2007

0.0

0.701

. 2007, 37(1):100-105

Experiment and numerical simulation on drag reduction for bodies of revolution using bionic scrobiculate ringed surface

1.Key Laboratory for TerrainMachine Bionics Engineering,Ministry of Education,Jilin University,Changchun 130022,China;2.College of Agricultu re,Jilin University,Changchun 130062,China

The effects of the scrobiculate rings arranged on the rearward of bodies of revolution on the base drag, skin friction drag and shock wave drag were investigated through wind tunnel tests and numerical simulation. The wind tunnel tests with Ma=1.79, and the Re=1.5×106 based on the maximal diameter of the body indicat that the scrobiculate ringed surface can reduce the base drag evidently, but it increases the viscous forebody drag including the skin friction drag and shock wave drag. The numerical simulation with SST k-ω turbulence model shows that the scrobiculate ringed surface reduces the viscous drag by 22.4% due to the vortex cushioning effect and driving effect produced by the low speed rotating flows formed in the rings. The scrobiculate rings also weaken the pumping action of the external flow on the base dead water region behind the body of revolution, and accordingly the base drag is reduced. However, the rings only reduce the pressure drag by 0.4% because the rings disturb the external flow and increase the shock wave drag.

通过风洞试验及数值模拟分析了置于旋成体后部的凹环表面结构对其底部阻力、摩擦
阻力及激波阻力的影响。马赫数为1.79、基于旋成体最大直径的雷诺数为1.5×10⁶的风洞
试验表明：凹环表面可显著减小旋成体的底部阻力，但却增大了包含摩擦阻力和激波阻力的粘
性前部阻力。利用SST k-ω湍流模型对试验优选模型进行了数值模拟，结果表明：凹环
内部低速旋转气流产生的涡垫效应和推动效应致使旋成体的摩擦阻力减小了22.4%，
凹环还能减弱外部气流对旋成体截尾底部死水区的抽吸作用，显著降低了底部阻力。但由
于凹环对气流的扰动增加了激波阻力，故包含底部阻力及激波阻力的压差阻力减小并不显
著，仅为0.4%。

2013

0.0

0.701

. 2013, 43(4):983-990 DOI:10.7964/jdxbgxb201304023

Characteristics of drag reduction of bionic dimpled surface of shell rubber ring of aerodynamic extinguishing cannon

1. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China; 2. College of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500,China; 3. Qiqihar Heavy CNC Equipment Co., Ltd., Qiqihar 161005, China

To reduce the frictional resistance between the barrel and the rubber seal ring of shell body during the launching process of aerodynamic extinguishing cannon, a bionic drag reduction technology of dimpled surface was applied to the rubber ring. The motion model was established for the dimpled drag reduction surface of the rubber seal ring. The effects of the characteristic diameter of bionic dimples on the rubber seal ring and the shell speed on the frictional resistance between barrel and shell body were investigated by numerical simulation. Results show that, at the same shell speed, with dimple characteristic diameter of 2 mm, the highest drag reduction effect, 17.191%, was obtained; with dimple characteristic diameter of 4 mm, the lowest drag reduction effect, 3.158, was obtained. It is revealed that the mechanism of the drag reduction is that, during moving inside the barrel, the lubricant stored in the dimples on the seal ring of shell spills over to lubricate the barrel wall and seal ring, which reduces the frictional resistance and thus increases the launching speed.

针对气动灭火炮炮弹发射过程中弹体橡胶密封圈与炮管之间摩擦阻力大的问题,将仿生凹坑表面减阻技术应用于弹体橡胶密封圈上。建立气动灭火炮橡胶密封圈仿生凹坑减阻运动模型,采用数值模拟方法,研究弹体橡胶密封圈仿生凹坑特征直径及弹体速度对橡胶密封圈与炮管之间摩擦阻力的影响。结果表明:在相同的弹体速度下,当灭火炮弹体橡胶密封圈仿生凹坑特征直径为2 mm时,减阻效果最佳,凹坑特征直径为4 mm时,减阻效果最差;最大减阻率为17.191%,最小减阻率为3.158%。仿生凹坑中存储的润滑油在弹体运动时,润滑油产生拖拽泼洒而溢流到炮管内壁,对炮管内壁和橡胶密封圈起到润滑作用,达到减小摩擦阻力以及提高炮弹发射速度的目的。

2009

1.08

0.0

2010

0.0

... 另外,前期对仿生射流减阻技术的研究都是基于单孔射流^[8],而多孔射流表面的流场结构与单孔相比具有较大的不同,多孔射流表面是否能够减阻以及减阻特性如何也有待进一步研究 ...

2005

0.0

0.474

. 2005, 13(2):120-128

Numerical analysis for a round turbulent buoyant jet in a cross flow

采用k-ε双方程模型,结合混合有限分析方法对横流中三维圆形垂直热水浮力射流进行了数值模拟.计算所得的温升分布与试验值较为吻合.对射流的流动结构、分叉现象、射流轨迹线等进行了预报,得出了基于速度场和温度场的射流轨迹线不同,横断面上的两个高温区的夹角范围与空气中所得结论一致,影响射流的主要因素是射流对来流的流速比等结论,从而证明了运用该数学模型对横流中三维圆形垂直热水浮力射流进行数值研究的有效性.

... 分析图4(a)可知,同时改变主流速度和射流速度使之保持流速比不变,减阻率几乎保持不变,说明流速比是影响射流流场的主要因素^[9] ...

2012

0.0

0.789

... 单孔、双孔和五孔射流的减阻率与流速比呈近似线性关系,即当主流速度不变时,射流速度越大减阻效果越好^[10] ...