基于遗传算法优化的BP神经网络的材料疲劳寿命预测

引用本文

闫楚良, 郝云霄, 刘克格. 基于遗传算法优化的BP神经网络的材料疲劳寿命预测. 44(6): 1710-1715
YAN Chu-liang, HAO Yun-xiao, LIU Ke-ge. Fatigue life prediction of materials based on BP neural networks optimized by genetic algorithm. Journal of Jilin University Engineering and Technology Edition, 44(6): 1710-1715 复制到剪切板

Permissions

基于遗传算法优化的BP神经网络的材料疲劳寿命预测

闫楚良, 郝云霄, 刘克格

北京飞机强度研究所,北京 100083

通信作者:郝云霄(1983-),女,博士.研究方向:飞机结构寿命与可靠性.E-mail:haoyunxiao_123@163.com

作者简介:闫楚良(1947-),男,研究员,博士生导师.研究方向:飞机结构寿命与可靠性.E-mail:yancl@sina.cn

基金:国家自然科学基金项目(50135010);

摘要

针对传统的材料疲劳寿命计算方法(概率统计法)误差较大的问题,在对材料疲劳寿命数据进行分类的基础上,采用基于遗传算法优化的BP神经网络方法,建立了应力集中系数、应力均值、应力幅值和材料的中值寿命之间的关系模型,针对具有有限寿命的数据进行寿命预测。实例验证结果表明,利用本文方法获得的预测结果与试验数据的相对误差均在5%以下,优于传统算法的预测精度,可以作为获取材料疲劳寿命数据的一种更为有效的手段。

关键词: 材料疲劳寿命; BP神经网络; 遗传算法; 疲劳寿命预测

中图分类号:O346.2;V215.5 文献标志码:A 文章编号:1671-5497(2014)06-1710-06

Fatigue life prediction of materials based on BP neural networks optimized by genetic algorithm

YAN Chu-liang, HAO Yun-xiao, LIU Ke-ge

Beijing Aircraft Strength Institute, Beijing 100083, China

Abstract

The error of traditional fatigue life algorithms of materials is big. To overcome this problem, a model of the relationship among stress concentration factor (K_t), stress average (S_m), stress amplitude (S_a) and median life (N50) was built using BP neural network combined with genetic algorithm. This model is based on the classification of fatigue life data of materials, and it can be used to predict fatigue lift of materials with finite life data. Experiment results show that, using this model the relative prediction error is below 5%, in another word, the prediction accuracy of this model is higher than that of the traditional prediction algorithms. So this model can be applied to prediction the fatigue life of materials.

Keyword: fatigue life of materials; BP neural networks; genetic algorithm; fatigue life prediction

Show Figures

0 引言

材料的P-S-N曲线是结构件进行寿命分析和疲劳可靠性设计的重要依据^{[ 1, 2, 3, 4, 5]}。获得P-S-N曲线的常规方法主要是基于传统的概率统计方法,近年来一些学者对此方法进行了相关的研究和改进,如建立广义S-N曲面^{[ 6]}、采用加权最小二乘法估计^{[ 7]}、使用Monte Carlo方法修正^{[ 8]}等。随着模拟仿真技术的发展,人工神经网络等技术被引入这方面研究中^{[ 9, 10, 11]},其中BP神经网络是目前应用最为广泛的一种误差逆传播神经网络^{[ 12]},可以为材料疲劳寿命估计提供一种新的方法。但该网络的初始权值和阈值是随机获取的,容易导致网络训练陷入局部最优以及延长收敛时间,通常采用遗传算法(GA)对其进行优化^{[ 13, 14, 15, 16]}。

本文采用BP神经网络方法预测材料的疲劳寿命,并引入遗传算法对其进行优化,建立预测模型;利用一个算例对此模型进行训练和检验。通过比较网络的训练效果,选择适当的网络参数,并将预测值与使用传统方法得到的计算值进行对比来验证此模型预测材料疲劳寿命的优势。

1 传统计算方法简介

由于构件在各种工况下受到随机循环载荷的作用,所以构件的疲劳寿命实际上是由循环应力幅值 S_a和循环应力均值 S_m共同控制的。循环最大应力 S_max与疲劳寿命 N的关系可用三参数 S-N曲线方程表示为:

$\begin{matrix} (S_{\max} - S_{0})^{m} N = C (1) \end{matrix}$

式中:三参数 S₀、 m、 C与材料、集合形状和应力比有关。其中 S₀为“理论疲劳极限”,即当 N→ ¥时的应力。

在给定应力均值 $\begin{matrix} S_{m}^{*} \end{matrix}$ 时:

$\begin{matrix} S_{\max} = S_{m}^{*} + S_{a} (2) \end{matrix}$

将式(2)代入式(1)得:

$\begin{matrix} S_{a} = {(\frac{C}{N})}^{\frac{1}{m}} + S_{0} - S_{m}^{*} (3) \end{matrix}$

引入等寿命曲线方程,本文采用对于塑性材料较为适用的Gerber方程:

$\begin{matrix} S_{a} = σ_{- 1} (1 - \frac{{S_{m}}^{2}}{{σ_{b}}^{2}}) (4) \end{matrix}$

式中: σ_b为抗拉强度; σ_-₁为对称循环疲劳强度。

将式(3)和 S_m = $\begin{matrix} S_{m}^{*} \end{matrix}$ 代入式(4)得:

$\begin{matrix} σ_{- 1} = \frac{{(\frac{C}{N})}^{\frac{1}{m}} + S_{0} - S_{m}^{*}}{1 - {S_{m}^{*}}^{2} / {σ_{b}}^{2}} (5) \end{matrix}$

将式(5)代入式(4),可得Gerber型广义 S-N曲面方程为:

$\begin{matrix} N = \frac{C}{[\frac{(σ_{b}^{2} - S_{m}^{* 2}) S_{a} + (σ_{b}^{2} - S_{m}^{2}) S_{m}^{*}}{σ_{b}^{2} - S_{m}^{2}} - S_{0}]^{m}} (6) \end{matrix}$

式中: σ_b、 $\begin{matrix} S_{m}^{*} \end{matrix}$ 为已知量;待定常数 S₀、 m、 C根据式(1)对材料疲劳寿命的试验数据统计处理求得。

对于航空领域常用材料LC4高强度铝合金板材,根据疲劳寿命试验数据^{[ 17]},求得其在不同应力集中系数 K_t和给定应力均值 $\begin{matrix} S_{m}^{*} \end{matrix}$ 下的Gerber型广义 S-N曲面方程。从数据中随机抽取5组样本,利用求得的 S-N曲面方程进行计算,并对比计算值与试验值,如表1所示。从表中可以看出,第2个样本和第4个样本的相对误差很大,均超过10%。这是由于经验公式本身以及概率统计处理过程都带有一定的不确定性,导致数据结果与真实值之间存在一定的偏差。

表1 LC4高强度铝合金板材的部分寿命试验值与计算值比较 Table 1 Comparison between the patial experimental data and computed data of fatigue life about LC4

2 神经网络预测模型

2.1 基于疲劳寿命特征的模型

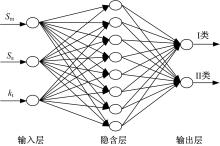
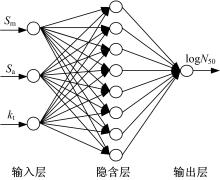
通常将材料的寿命分为长、中、短三个寿命区,中、长寿命区的分界线一般为10⁷次,若寿命超过10⁷次,可视为无限寿命,反之则视为有限寿命。无限寿命可不进行数值预测,有限寿命利用神经网络进行预测。设计两种BP神经网络模型分别实现分类和数值预测的功能。构件的寿命与多种因素有关,其中材料本身的性质、应力集中系数以及应力水平是主要影响因素,因此以应力集中系数 k_t、应力均值 S_m、应力幅值 S_a作为输入变量来描述材料的中值寿命 N₅₀。

2.2 BP神经网络模型

BP神经网络是一种单向传播的多层前向网络,包括输入层、隐含层和输出层,采用的算法是误差反向传播算法,即BP算法^{[ 9]}。该算法依次计算隐含层输出 H_j=g( $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ w_ij-a_j)和输出层的输出 f_k= $\begin{matrix} \overset{l}{\sum_{j = 1}} \end{matrix}$ H_jw_jk-b_k,根据输出值和真实值的误差 e=y_k-f_k更新网络的权值和阈值为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} w_{ij} = w_{ij} + η H_{j} (1 - H_{j}) x_{i} \overset{m}{\sum_{k = 1}} w_{jk} e_{k} \\ w_{jk} = w_{jk} + η H_{j} e_{k} \\ a_{j} = a_{j} + η H_{j} (1 - H_{j}) \overset{m}{\sum_{k = 1}} w_{jk} e_{k} \\ b_{k} = b_{k} + e_{k} \end{matrix} \\ (7) \end{matrix} \end{matrix}$

式中: j=1,2,…, l,其中 l为隐含层节点数; k=1,2,…, m,其中 m为输出层节点数; n为输入层节点数; g为隐含层和输出层神经元之间的传递函数; w_ij和 a_j分别为隐含层的权值和阈值; w_jk和 b_k分别为输出层的权值和阈值; η为网络学习速率。

选取模型的输入层均为 k_t、 S_m、 S_a三个单元,分类网络输出层为有限寿命所属的Ⅰ类和无限寿命所属的Ⅱ类两个节点单元;预测网络的输出层为log N₅₀一个节点单元;隐含层节点数 l根据公式 l= $\begin{matrix} \sqrt[]{n + m} \end{matrix}$ +a( a∈[1,10])可得范围为[3,12],本文取值8;学习速率 η取0.2,隐含层和输出层神经元之间的传递函数采用Sigmoid函数 g( x) =1 /(1 +e^-x), 其结构图如图1和图2所示。

	Figure Option View Download New Window
	图1 分类功能的BP神经网络结构图Fig.1 BP neural network with classification

	Figure Option View Download New Window
	图2 预测功能的BP神经网络结构图Fig.2 BP neural network with prediction

2.3 预测网络模型的遗传算法优化

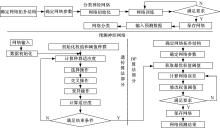
GA算法的基本思想是用个体代表网络的初始权值和阈值,用个体值初始化的BP神经网络交叉、变异操作寻找最优个体,即最优的BP神经网络权值和阈值。本文通过在MATLAB软件中编程实现GA算法,主要包括以下步骤:

(1)使用浮点数编码方式实现种群初始化。个体编码长度为网络所有权值个数( n×m+l×m)和阈值个数( l+m)之和。

(2)把BP网络的预测输出值和真实值之间的误差平方和作为个体适应度,计算表达式为: F=c $\begin{matrix} \overset{m}{\sum_{i = 1}} \end{matrix}$ ( y_i-f( x_i))²,式中 m为网络输出层节点数; y_i为真实值; f( x_i)为预测值; c为惩罚参数。

(3)选择操作采用最优保存策略,每一代群体中的最优个体直接进入下一代,余下个体采用轮盘赌法选择,每个个体被选择到下一代参加遗传操作的概率为 p_i=f_i/ $\begin{matrix} \overset{N}{\sum_{j = 1}} \end{matrix}$ f_j,式中 f_i=k/F_i, F_i为个体 i的适应度值, k表示染色体的次序。

(4)交叉操作采用实数交叉法,第 k个染色体 a_k和第 l个染色体 a_l在 j位的交叉操作方法如下:

$\begin{matrix} \begin{matrix} a_{kj} = a_{kj} (1 - b) + a_{lj} b \\ a_{lj} = a_{lj} (1 - b) + a_{kj} b (8) \end{matrix} \end{matrix}$

式中: b是[0,1]间的随机数。

(5)变异操作方法如下:

$\begin{matrix} \begin{matrix} a_{ij} = \{\begin{matrix} a_{ij} = a_{ij} + (a_{ij} - a_{\max}) \times f (g), r > 0.5 \\ a_{ij} = a_{ij} + (a_{\min} - a_{ij}) \times f (g), r \leq 0.5 \end{matrix} \\ (9) \end{matrix} \end{matrix}$

式中: a_max为 a_ij的上界; a_min为 a_ij的下界; f( g) =r₂ $\begin{matrix} (1 - g / G_{\max})^{2} \end{matrix}$ , r₂为一个随机数; g为当前迭代次数; G_max是最大进化次数; r为[0,1]间的随机数。

整个算法流程如图3所示。

	Figure Option View Download New Window
	图3 算法流程图Fig.3 Flow diagram of BP neural network with genetic algorithm

3 实例及对比

选用LC4高强度铝合金板材的疲劳寿命试验数据作为神经网络的样本^{[ 17]}。样本共有78对数据,其中66对属于Ⅰ类(有限寿命),12对属于Ⅱ类(无限寿命)。进行分类时,Ⅱ类的样本较少,会导致神经网络的泛化性降低,因此利用插值法将Ⅱ类数据扩展为36对。从中随机抽取Ⅰ类数据中的34对、Ⅱ类数据中的24对作为训练样本,余下数据作为测试样本。

由于 k_t、 S_m、 S_a和 N₅₀的数值分布范围较广且较分散,为保证网络在训练过程中收敛,避免因为输入输出数据数量级差别较大而造成网络预测误差较大。在训练之前,首先对其进行归一化处理,使输入和输出变量的值处于[-1,1]之间。训练结束后,再将数据进行反归一化,还原成实际值。数据归一化方法采用最大最小法。函数形式如下:

$\begin{matrix} x_{k} = (x_{k} - x_{\min} \frac{)}{(} x_{\max} - x_{\min}) (10) \end{matrix}$

式中: x_min为数据序列中的最小值; x_max为数据序列中的最大值。

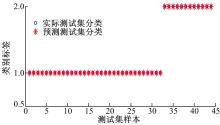
分类结果如图4所示,从图中可以看出,分类结果完全正确。

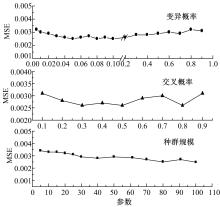
	Figure Option View Download New Window
	图4 测试样本的实际分类和预测分类比较Fig.4 Predicted classification and true classification about test data

从Ⅰ类的66对样本中随机抽取61对数据作为训练样本,5对数据作为检测样本。遗传算法部分影响网络性能的参数为种群规模、交叉概率和变异概率,根据相关研究^{[ 13, 14, 15]},这三者的经验取值范围分别为20~160、0.25~1.0、0.005~0.1,随着参数取值的变化,网络性能的变化与所研究的具体对象有关。本文使用预测值与实际值的均方误差和(MSE)作为衡量网络性能最常用的参考指标,MSE越小,表示网络预测性能越好。结合寿命预测实例,研究了在上述取值范围内,遗传算法进化次数为100时,三个参数对网络训练性能的影响,其结果如图5所示。

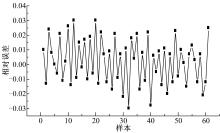
	Figure Option View Download New Window
	图5 遗传算法参数对网络性能的影响Fig.5 Influence of parameter in genetic algorithm to network property

由图5可知,随着种群规模的增大,MSE逐渐缓慢减小。种群规模越小,遗传算法的运算速度越高,但是种群的多样性降低,容易引起遗传算法早熟,出现假收敛,但种群规模较大时,又会使运算效率降低。随着交叉概率的增大,MSE逐渐减小,在0.3~0.5范围内,MSE趋于平缓,而后又逐渐增大。这是由于交叉概率越大,群体中产生的新模式越多,但已形成的优良模式也越容易遭到破坏,使搜索的随机性太大;而太小则会使发现优良新个体的速度太慢,导致搜索阻滞。变异概率的变化对MSE的影响与交叉概率相似,取值太大使遗传算法在整个搜索空间内跳跃幅度增大,成为随机搜索;太小则使其在特别区域进行局部搜索,引起遗传算法早熟,对于本文的模型,取值为0.05~0.1时MSE较小且变化平稳。当上述三个参数取值分别为85、0.45、0.06时,训练样本预测值与真实值的相对误差如图6所示。

从图6中可以看出,预测值和真实值的相对误差均在5%以内,训练效果较为理想。

	Figure Option View Download New Window
	图6 训练样本预测值与真实值的相对误差Fig.6 Relative error between the prediction and true value of training data

利用测试样本对训练好的网络进行验证。预测值、利用传统方法得到的计算值以及它们与试验结果的误差均列于表2中。比较预测值和计算值的相对误差可以看出,5个样本预测值的相对误差绝对值均在5%以内;第1、3、5个样本计算值的相对误差绝对值在5%以内,而第2个和第4个样本的计算值却超过10%,偏离较大;除第1个样本预测值的相对误差略大于计算值外,其他几个样本的相对误差都小于计算值。从整体数据对比可以看出,预测值要优于计算值,预测效果比较理想。

表2 神经网络预测结果 Table 2 Prediction of neutral network

4 结论

针对传统的材料疲劳寿命计算方法与实际值之间误差较大的问题,建立了基于遗传算法优化的BP神经网络的寿命预测模型。实例预测结果表明:

(1)利用该模型预测的材料疲劳寿命与真实值的相对误差绝对值均在5%以内,预测精度较高,满足使用要求。

(2)与利用广义S-N曲面方程的传统计算方法相比,预测误差相对较小,整体上更为接近真实值,可以作为获取材料的疲劳寿命数据的一种更为有效的手段。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	高镇同, 熊峻江. 疲劳可靠性[M]. 北京: 北京航空航天大学出版社, 2000. [本文引用:1]
[2]	闫楚良, 刘克格. 飞机结构经济寿命设计与可靠性评定[M]. 北京: 航空工业出版社, 2010. [本文引用:1]
[3]	Yan Chu-liang, Liu Ke-ge. Fatigue scatter factor of whole life and reliability of aircraft structure service life[J]. Advanced Materials Research, 2008, 44-46: 739-744. [本文引用:1]
[4]	Yan Chu-liang, Liu Ke-ge. Theory of active reliability-based design for predetermined life of structures[J]. Advanced Materials Research, 2008, 44-46: 745-750. [本文引用:1]
[5]	Yan Chu-liang, Liu Ke-ge. Theory of economic life prediction and reliability assessment of aircraft structures[J]. Chinese Journal of Aeronautics, 2011, 24: 164-170. [本文引用:1] [JCR: 0.438] [CJCR: 0.665]
[6]	闫楚良, 高镇同. 疲劳性能广义S-N曲面[J]. 机械工程学报, 1999, 34(1): 103-105. Yan Chu-liang, Gao Zhen-tong. Generalized S-N curved surface of fatigue character[J]. Journal of Mechanical Engineering, 1999, 34(1): 103-105(In Chinese). [本文引用:1] [CJCR: 0.544]
[7]	李宏双, 吕震宙. 估计疲劳寿命三参数P-S-N曲线的新方法[J]. 机械强度, 2007, 29(2): 300-304. Li Hong-shuang, Lyu Zhen-zhou. New method for estimating fatigue life three-parameter P-S-N curves[J]. Journal Mechanical Strength, 2007, 29(2): 300-304. [本文引用:1] [CJCR: 0.533]
[8]	赵永翔杨冰. 不完善概率疲劳S-N曲线的Monte Carlo修正[J]. 机械工程学报, 2011, 47(12): 170-174. Zhao Yong-xiang, Yang Bing. Monte carlo mondification of imperfect probabilistic fatigue S-N curves[J]. Journal of Mechanical Engineering, 2011, 47(12): 170-174. [本文引用:1] [CJCR: 0.544]
[9]	孟广伟, 沙丽蓉, 李锋, 等. 基于径向基函数神经网络响应面法的装载机动臂疲劳可靠性[J]. 吉林大学学报: 工学版, 2009, 39(6): 1516-1520. Meng Guang-wei, Sha Li-rong, Li Feng, et al. Fatigue reliability analysis of loader boom based on RBF-NN response surface method[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(6): 1516-1520. [本文引用:1] [CJCR: 0.701]
[10]	Rodney D Averett, Mary L Realff. Comparative post fatigue residual property predictions of reinforced and unreinforced poly(ethylene terephthalate) fibers using artificial neural networks[J]. Composites Part A: Applied Science and Manufacturing, 2010, 41(3): 331-344. [本文引用:1] [JCR: 2.744]
[11]	刘仁云, 于繁华, 刘军. 基于小波神经网络的简支梁桥损伤识别[J]. 吉林大学学报: 工学版, 2009, 39(2): 413-416. Liu Ren-yun, Yu Fan-hua, Liu Jun. Damage detection for simply supported based on wavelet neural network[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(2): 413-416. [本文引用:1] [CJCR: 0.701]
[12]	马锐. 人工神经网络原理[M]. 北京: 机械工业出版社, 2010. [本文引用:1]
[13]	瞿宜锋, 李鸿雁, 刘寒冰, 等. 用遗传算法优化神经网络初始权重的方法[J]. 吉林大学学报: 工学版, 2003, 33(2): 45-50. Qu Yi-feng, Li Hong-yan, Liu Han-bing, et al. Method for optimizing initial werghts of ANNs by GAs[J]. Journal of Jilin University(Engineering and Technology Edition), 2003, 33(2): 45-50. [本文引用:1] [CJCR: 0.701]
[14]	Zhou Nan, Zhang Ji-xiong. Genetic algorithm coupled with the neural network for fatigue properties of welding joints predicting[J]. Journal of Computers, 2012, 7(8): 1887-1894. [本文引用:1]
[15]	李敏强, 寇纪凇. 遗传算法的基本理论与应用[M]. 北京: 科学技术出版社, 2003. [本文引用:1]
[16]	李英, 李元春. 基于神经网络和遗传算法的采油控制系统[J]. 吉林大学学报: 工学版, 2006, 36(1): 83-86. Li Ying, Li Yuan-chun. Oil pumping control system based on neural network and genetic algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2006, 36(1): 83-86. [本文引用:1] [CJCR: 0.701]
[17]	高镇同. 疲劳性能试验设计和数据处理[M]. 北京: 北京航天航空大学出版社, 1999. [本文引用:2]

2000

0.0

2010

0.0

2008

0.0

2008

0.0

2011

0.438

0.665

. 2011, 24:164-170 DOI:10.1016/S1000-9361(11)60020-4

Liu Ke-ge. Theory of economic life prediction and reliability assessment of aircraft structures

a. Beijing Aircraft Structure Institute, Beijing 100083, China;<br />b. School of Aeronautics Science and Engineering, Beihang University, Beijing 100191, China

The theory of economic life prediction and reliability assessment of aircraft structures has a significant effect on safety of aircraft structures. It is based on the two-stage theory of fatigue process and can guarantee the safety and reliability of structures. According to the fatigue damage process, the fatigue scatter factors of crack initiation stage and crack propagation stage are given respectively. At the same time, mathematical models of fatigue life prediction are presented by utilizing the fatigue scatter factors and full scale test results of aircraft structures. Furthermore, the economic life model is put forward. The model is of significant scientific value for products to provide longer economic life, higher reliability and lower cost. The theory of economic life prediction and reliability assessment of aircraft structures has been successfully applied to determining and extending the structural life for thousands of air-planes.

1999

0.0

0.544

... 获得P-S-N曲线的常规方法主要是基于传统的概率统计方法,近年来一些学者对此方法进行了相关的研究和改进,如建立广义S-N曲面^[6]、采用加权最小二乘法估计^[7]、使用Monte Carlo方法修正^[8]等 ...

2007

0.0

0.533

2011

0.0

0.544

2009

0.0

0.701

. 2009, 39(6):1516-1520

Fatigue reliability analysis of loader boom based on RBF-NN response surface method

1.State Key Laboratory of Automobile Dynamic Simulation, Jilin University,Changchun 130022,China|2.College of Mechanical Science and Engineering,Jilin University,Changchun 130022,China

The response surface method based on the radial basis function neural nelwork(RBF-NN) was adopted to analyze the fatigue reliability of a loader boom.When the limit state function of structure is complex or highly nonlinear,it is time-consuming or cumbersome to carry out reliability analysis with traditional methods.The RBF-NNbased response surface method provides an effective means for the reliability analysis of the large scale structures.The working process of a loader machine was analyzed with the analytical approach combining the finite element method software ANSYS,the stress and strain histories of the loader boom were calculated by rainflow algorithm,consequently the fatigue life of the structure could be derived by the local stressstrain analysis.The RBF-NN based response method was used to fit the limit state function of the structure as well as its derivatives,so as to calculate the reliability of the structure.The examplified numerical results showed the proposed method is capable of solving the industrial-scale fatigue reliability problems.

采用解析法与有限元软件ANSYS相结合的方法对装载机的工作过程进行计算，根据雨流法建立工作过程中装载机动臂的应力及应变的时间历程，通过局部应力应变分析得到结构的疲劳寿命。运用神经网络响应面来拟合结构的极限状态函数及其偏导数，利用可靠度理论分析了装载机动臂的疲劳寿命可靠性。

... 2 BP神经网络模型BP神经网络是一种单向传播的多层前向网络,包括输入层、隐含层和输出层,采用的算法是误差反向传播算法,即BP算法^[9] ...

2010

2.744

0.0

. 2010, 41(3):331-344 DOI:10.1016/j.compositesa.2009.09.020

Comparative post fatigue residual property predictions of reinforced and unreinforced poly(ethylene terephthalate) fibers using artificial neural networks

Abstract

A set of experiments has been performed on poly(ethylene terephthalate) (PET control) and PET fibers with vapor grown carbon nanofibers (PET–VGCNF) to assess the mechanical integrity of the materials due to a repeated cyclic loading. Artificial neural networks (ANNs) have been used to examine the residual strength and elastic modulus degradation behavior of the filaments as a function of the input mechanical testing variables (maximum fatigue stress – σ_max, stress ratio – R, # cycles – N, undeformed modulus – E) and a damage variable that has been identified as the residual strain from fatigue, ε_R. The relationship of how these input variables relate to the degradation of the elastic modulus, E, and the fracture strength, σ_f, has been determined. The results indicate that ANNs can be used to predict the residual strength and modulus degradation behavior of PET and PET/VGCNF single filaments under various loading conditions. Backpropagation (BP) with momentum and conjugate gradient algorithms have been utilized to successfully train a multilayer perceptron (MLP) network for modeling the mechanical behavior of single polymeric filaments subsequent to fatigue loading. Also, the mechanical behavior of the PET control and PET–VGCNF differs as a function of the input fatigue conditions prescribed. The main difference was that the PET control samples exhibited a distinct hardening effect in the low residual strain limit and this was not observed for the PET–VGCNF samples. The neural networks used in this work were successful at replicating the hardening behavior for the PET control samples and the mechanical behavior changes for the PET–VGCNF samples as a function of σ_max, R, and ε_R.

2009

0.0

0.701

. 2009, 39(2):413-416

Damage detection for simply supported based on wavelet neural network

1. School of Mathematics, Changchun Normal University, Changchun 130032, China;2. School of Computer Science &|Technology, Changchun Normal University, Changchun 130032, China

The wavelet neural network(WNN) is applied in many fields for its advantages of fast convergence，simple structure and computation since it has been presented. According to its strongly approaching ability to single dimensional signals, the Grey Relevancy Analysis theory is adapted to analyze the characteristic parameters and damage index of structural damage. The obtained relevancy degree of parameters is regarded as characteristic parameters of dynamic structure, and is transformed into weight value of singledimension input. Furthermore, the WNN model is presented with the Grey Relevancy Analysis. In order to improve the convergence ability and approaching effect, the study algorithm of WNN is ameliorated by local study policy. The simulation result indicates that the proposed method is superior to traditional Neural Network model.

针对小波神经网络对一维信号逼近能力强的特点，利用灰色理论中的关联分析法，对结构损伤特征参数和损伤指标进行灰关联分析，将所获得的参数间关联度作为把结构动态特征参数整合为一维输入量的权值，进而提出了基于灰色关联分析的小波神经网络模型。为提高网络的收敛能力和逼近效果，应用局部学习策略改进了小波神经网络的学习算法。仿真结果表明，利用上述方法进行结构损伤识别，识别结果明显优于传统的神经网络模型。

2010

0.0

... 随着模拟仿真技术的发展,人工神经网络等技术被引入这方面研究中^[9,10,11],其中BP神经网络是目前应用最为广泛的一种误差逆传播神经网络^[12],可以为材料疲劳寿命估计提供一种新的方法 ...

2003

0.0

0.701

2012

0.0

2003

0.0

2006

0.0

0.701

1999

0.0

... 对于航空领域常用材料LC4高强度铝合金板材,根据疲劳寿命试验数据^[17],求得其在不同应力集中系数K_t和给定应力均值 Sm* ...

... 3 实例及对比选用LC4高强度铝合金板材的疲劳寿命试验数据作为神经网络的样本^[17] ...