热成形技术因其具有回弹小、比强高等优点已获得了汽车制造厂商的极大关注并得到了广泛应用。基于常规和半热成形工艺特征淬火过程,对热成形产品不同区域进行不同冷却速率的淬火从而实现零件硬度的梯度分布,构建一种新型强度-硬度复合材料,使得热成形技术在产品创新应用中呈现出蓬勃的生命力^{[ 1, 2, 3]}。

热成形产品的机械性能与淬火开始温度和过程阶段冷却速率密切相关^{[ 4]}。不同的降温速率下得到的微观组织类别及组分不同,导致其强度、硬度等机械性能也不同。对板料热成形过程中冷却速率对热成形产品机械性能的影响进行预测,对热成形产品的早期开发具有重要意义。近年来,国内外学者主要基于非扩散性马氏体相变动力学理论,采用Kirkaldy-Venugopalan模型预测成形过程中的马氏体体积分数,并根据连续等温冷却CCT曲线建立冷却速率与硬度的对应关系,从而建立数值仿真预测模型^{[ 5, 6, 7]}。该模型局限性在于依赖钢种化学成分含量及恒定冷却速度工况下的冷却速率-硬度关系建立耦合预测关系,无法真实地反映热成形过程非等温马氏体转变对应关系。此外,实际热成形零件坯料不同部位在成形过程中的降温速率也并非恒定参数,采用上述方法很难保证预测结果符合实际产品的强度-硬度分布规律。

本文基于非等温淬火热成形分区冷却试验,建立了符合实际的热成形材料淬火阶段冷速与机械性能的对应关系,采用量纲分析和反推法获得了热成形材料冷却速率-机械强度-硬度指数模型。编制用户子程序将该模型引入到自主开发的软件KMAS_HF平台中,针对典型U形热成形件淬火后的强度、硬度数值仿真预测进行模型有效性验证。结果表明:该模型对材料热成形后的机械性能预测具有很好的适用性和可靠性,可为新型热成形强度硬度复合产品性能预测及梯度硬度热成形模具设计开发提供指导。

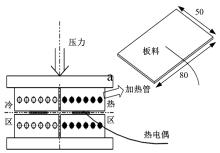
分区冷却方法通过调整模具的温度,控制淬火过程不同区域板料淬火速率从而获得零部件不同区域强度、硬度的差异性分布。试验所用设备为40 t快速液压机,试验装置为分区冷却平板模具(见 图1),该装置包含3部分:①带孔平板模具;②加热管,对模具热区进行加热;③闭环控温系统,反馈调节控制热区温度范围为20~500 ℃。上下模接触板及板料分别布置K型热电偶以准确采集模具和板料的温度变化。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 分区冷却模具Fig.1 Divided stage cooling tool

试验材料为热轧低碳硼合金钢22MnB5,化学成分如 表1所示。淬火前钢的抗拉强度为600 MPa,硬度为210 HV;淬火后,其抗拉强度可高达1500 MPa。试验板料厚度为1.6 mm。

表1

Table 1

表1(Table 1)

表1 低碳硼合金22MnB5的化学成分(质量分数%) Table 1 Chemical composition of low carbon boron alloy 22MnB5(%) C Si Mn P S Cr Ti B 0.24 0.27 1.14 0.015 0.001 0.17 0.036 0.003

表1 低碳硼合金22MnB5的化学成分(质量分数%) Table 1 Chemical composition of low carbon boron alloy 22MnB5(%)

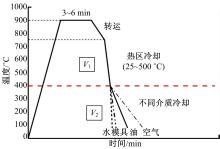
试验过程:将板料放入加热炉内升温到900 ℃,并保温以确保板料均匀奥氏体化,然后将板料取出迅速转移到平板模具上,模具上的托料装置用以支撑红热板料使其在成形前均匀空冷,避免出现局部冷却不均的现象。当板料降温至最佳成形温度750 ℃时,冲压淬火至马氏体相变(Ms点)温度400 ℃^{[ 8, 9]},然后迅速转移至水、模具等其他介质中保压淬火,试验控制曲线如 图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 分区冷却试验方案图Fig.2 Scheme diagram of divided stage cooling test

把从热成形淬火开始温度(750 ℃)至降温结束温度(200 ℃)区间内的实际降温速率定义为 V₀,以22MnB5钢马氏体转变开始Ms点为界定义热成形过程阶段冷速^{[ 9]}。将板料在750~400℃的冷却速率定义为一次冷却速率 V₁,400~200℃的冷却速率定义为二次冷却速率 V₂。为了控制实现不同的 V₁和 V₂,先将板料放置在模具热区进行冷却,通过调整模具温度和合模压力来获取不同序列的 V₁值;在400~200 ℃温度区间,板料被转移到不同的介质中进行冷却,包括水、油、模具、空气等,其中模具冷却又可以通过控制其保压时间和压力来进行调整,从而获取不同的 V₂值(见 表2)。通过对热电偶准确采集到板料芯部温度,并用YOKOGAWA MX100温度数据采集系统进行板料温度的实时采集。通过对不同组别试验分别获取的样件进行单向拉伸以获取机械性能,采用MHV-1000型显微硬度计测量样件硬度。

表2

Table 2

表2(Table 2)

表2 不同工况阶段冷却速率实现方式组合 Table 2 Combinations of cooling rate under different working conditions V1(750~400 ℃) V2(400~200 ℃) 模具温度/℃ 合模压强/MPa 淬火介质 备注 25 5 水 直接淬火 100 10 油 油淬 200 20 模具 分区模冷 300 30 空气 风冷 400 - - -

表2 不同工况阶段冷却速率实现方式组合 Table 2 Combinations of cooling rate under different working conditions

热成形过程中,22MnB5钢的微观组织发生相变,其机械性能也发生变化,机械性能不仅受淬火条件的影响,而且与机械强度和硬度、延伸率也密切相关^{[ 10]}。基于分区冷却平板试验获得全域冷却区间(750~200 ℃) V₀的冷却速率-强度-硬度试验结果,如 图3所示。从 图3可知,热成形钢硬度为239~538 HV,抗拉强度为591~1694 MPa,延伸率从19.9%逐步下降至7.6%。随着冷却速度的增加,板料的硬度和抗拉强度逐渐增加,而延伸率则逐渐减小。

图3

Fig.3

	Figure Option ViewDownloadNew Window
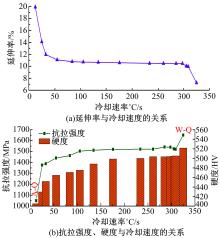	图3 热成形钢机械性能与全域冷却速度 V(750~200℃)的对应关系Fig.3 Relations between mechanical properties and global cooling rate V(750~200℃)for hot forming steel

进一步分析计算各硬度值对应的一次冷却速率 V₁和二次冷却速率 V₂情况。结果发现:硬度随 V₁的增加而明显增大,当 V₁达到一定值后硬度的增大趋势减缓;而硬度与 V₂的关系则不甚明显。经微观分析可知,当 V₁>60 ℃/s时,钢板不会生成铁素体、贝氏体等组织,选取 V₁为60~70 ℃/s时的工况绘制的图,如 图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
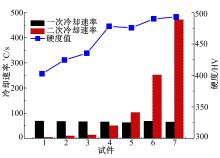	图4 热成形高强度钢冷却速率 V2与硬度的变化规律( V1=60~70 ℃/s)Fig.4 Curve of V2 and hardness of hot forming steel( V1=60~70 ℃/s)

当 V₂较高时,钢板硬度值达到饱和,组织为含量高达95%以上的板条状马氏体。随着冷却速率的下降,硬度也减小,当 V₁=60 ℃/s, V₂=5 ℃/s时,硬度下降至400 HV。在Ms点以上进行快速冷却无法得到单一的马氏体, V₂下降也会导致硬度下降至400 HV;若 V₂远低于 V₁,从连续等温转变CCT曲线可知,这种情况下只能得到硬度约为400 HV的含有针状渗碳体的马氏体和板条状马氏体的混合组织。马氏体相变后的冷却时间较长,该自回火过程使得针状渗碳体析出,从而导致硬度下降, V₂变小会使自回火的效果增强,进而硬度下降。

基于分区冷区试验获得冷却速率、强度及硬度三者之间的关系,采用量纲分析法^{[ 11, 12]}建立热成形高强度钢冷却速率-强度-硬度规律指数模型。其目标函数为:

H=H(V1,V2,V0,E,σ)(1)

将式(1)表示为一般表达式:

F(V1,V2,V0,E,σ,H)=0(2)

式中: H为硬度; σ为抗拉强度; V₀为22MnB5钢达到淬火的临界 V₁( V₀=60 ℃/s); E为杨氏模量。

在力学中,任何一个物理量的量纲都可以用三个基本量纲(质量 M、长度 L和时间 T)表示,目标函数中所涉及到的物理量及其量纲为:

[V1]=LT-1;[E]=L-1MT-2[V2]=LT-1;[σ]=L-1MT-2[V2]=LT-1;[H]=L-1MT-23

由此可得到量纲矩阵:

AT=1111-1-1-10000111-1-1-1-1-2-2-24

对于量纲矩阵, rank A^T =2,由Buckingham Pi定理可知式(2)与下式等价:

F(π1,π2,π3,π4)=0(5)

式中: F为一个未定的函数关系, π_s为无量纲量,且 π_s可表示为:

πs=∏i=1nxiβi(s)6

而 βi(s) =( β1(s) β2(s)… βn(s))为式(6)线性齐次方程组的基本解向量。

ATβ=0(7)

因为 n-rank A=4,因此方程组有4个基本解向量:

β1=(0,0,0,-1,1,0)Tβ2=(1,0,-1,0,0,0)Tβ3=(0,1,-1,0,0,0)Tβ4=(0,0,0,0,-1,1)T8

由式(8),可给出4个无量量纲:

π1=σE-1π2=V1V0-1π3=V2V0-1π4=Hσ-19

由式(5)(9)可得如下的硬度表达式:

Hσ=Π(σE,V1V0,V2V0)(10)

式中: Π为一个未知函数,其具体形式采用反推法推导确定。

当 V₂>20 ℃/s时,硬度和抗拉强度主要依赖 V₁;当 V₂≤20 ℃/s时,出现显著的回火过程,板料机械性能下降,因此建立数学模型时可采用 V₂的分段函数,从而式(10)可以转换为:

Hσ=Πα(σE,V1V0),V2>20℃/sΠβ(σE,V1V0,V2V0),V2≤20℃/s11

采用数据反推法^{[ 13]}求解 Π_α, Π_β的数学表达式。为保证函数的连续性和稳定性,利用Matlab非线性数值分析算法,对试验数据进行指数函数拟合,得到拟合的硬度-冷却速率指数模型、强度-硬度指数模型如式(12)(13)所示:

HH0=α+βexpχV1V0+δexpεV1V0, V2>20℃/sα+βexpχV1V0+δexpεV1V0exp(1+a3V22V0b-(1+a)3V22V0c+d, V2≤20℃/s12Hσ=ρ+θexpζV1V0σEξ, V2>20℃/sψ+φexpτV1V0expφV2V0σEξ, V2≤20℃/s13

式中: H₀为钢板淬火前硬度;对于热成形硼合金钢22MnB5,式中常数取值如 表3所示。

表3

Table 3

表3(Table 3)

表3 冷却速率-机械强度-硬度指数模型系数 Table 3 Coefficients for cooling rate-mechanical strength-exponential index model α β χ δ ε a b c d 3.1410 -2.2585 -1.2045 -0.3769 -0.1094 0.1339 3.3227 0.0911 -0.376 ρ θ ζ ξ ψ φ τ ϕ ϑ 0.3847 1.9379 -12.4378 -0.0863 0.3844 1.9553 -13.0659 4.0600 -0.0870

表3 冷却速率-机械强度-硬度指数模型系数 Table 3 Coefficients for cooling rate-mechanical strength-exponential index model

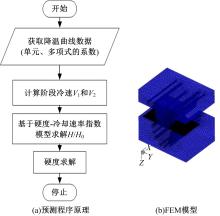
通过建立的冷却速率-强度-硬度指数模型,采用显式预测模型对热成形产品的硬度分布进行预测。基于式(12),利用板料在热成形过程中的降温曲线进行22MnB5钢的硬度性能预测。采用四次多项式拟合数值仿真所得的降温曲线,将多项式系数作为预测程序初值,编制预测程序框图如 图5(a)所示。通过Fortran语言编写用户子程序,将程序应用到自主开发的商业CAE软件KMAS_HF热成形模块中。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 预测程序原理图及FEM模型Fig.5 Program graph of prediction procedure and FEM model

采用U形模具进行仿真和试验研究。仿真三维FEM网格模型如 图5(b)所示,模型采用BT壳单元。在热力耦合数值仿真中,考虑了温度变化对比热容和热导率的影响,接触热传导系数采用NUMISHEET 2008 BM03基准^{[ 14]}中提供的随压强变化的函数关系。 V₁, V₂和硬度三维曲线图如 图6所示,当 V₂≥20 ℃/s时, V₁是影响热成形产品强度的最主要因素,且硬度随着冷却速率增大而增大;而 V₂对硬度的影响主要体现在0~20 ℃/s区间, V₂越小,回火越明显,硬度越低;当 V₂≤5 ℃/s时,出现迅速上翘的趋势,综上可知,当 V₂=5 ℃/s时,材料的自回火效应已接近极限。

图6

Fig.6

	Figure Option ViewDownloadNew Window
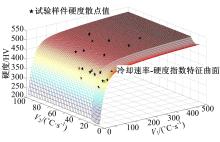	图6 冷却速率-强度-硬度指数模型预测三维图Fig.6 Three-dimensional diagram of cooling rate-Mechanical strength-exponential index model

试验所用板料厚1.6 mm,模具间隙2.06 mm。采用模具与不匹配的板料进行试验,目的在于使成形后得U形零件横截面上具有一定的硬度梯度。试验时,先将板料加热到900 ℃^{[ 15]},保温6 min,然后放置到水冷模具的托料装置上,空冷至750 ℃后迅速冲压成形并保压,保压压强为20 MPa,保压时间为30 s。

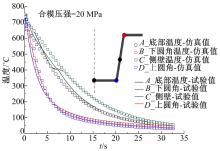
板料特征位置点( A—底部; B—下圆角; C—侧壁; D—上圆角)的降温曲线如 图7所示,以合模压强20 MPa为例进行对比分析,仿真结果能较好地与试验结果吻合。板料在上下圆角位置降温最快,并且下圆角由于先与模具接触而在初始阶段降温稍快;在模具侧壁和底部对应位置,板料降温速率有明显的减缓趋势,特别是在侧壁位置。侧壁位置间隙的存在,导致板料处于悬空拉伸状态,保压时的实际压力比较小,降温慢。并呈现接近下圆角处间隙偏大,降温慢的现象,这跟板料在此处拉扯严重导致板料变薄有很大关系。在底部位置,板料在成形的1~2 s内成弧状并与模具保持一定间隙,降温较慢,合模后则降温较快。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 板料测量点降温曲线Fig.7 Cooling curves of measuring points on sheet metal

图8为仿真得到的硬度分布云图及微观SEM金相,从图中可知:侧壁位置降温慢,淬火不充分,硬度只有394.12 HV,而其他3个位置点都实现了较充分淬火,硬度大于450 HV。计算仿真中板料4位置点的 V₁和 V₂,并将硬度值的仿真结果与试验结果进行对比,试验值与仿真预测值误差范围为20~24 HV,预测数据吻合程度良好。

图8

Fig.8

	Figure Option ViewDownloadNew Window
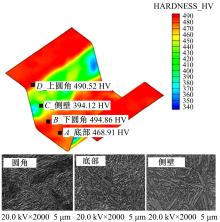	图8 板料的硬度分布云图及测量点微观SEM硬度值Fig.8 Hardness distribution of FEM prediction and SEM microstructure for measuring points after quenching

由 表4可知,仿真的降温速率比试验值大,因而其硬度和强度也稍大,这是因为试验时板料表层会产生氧化皮,阻碍了热量的流通,因而冷却速度慢。在试验测量范围内,抗拉强度与硬度之间存在近似的正相关关系,即硬度越大,抗拉强度越大。成形过程中,板料上下圆角位置与模具接触较早,且保压时也获得了较大的实际保压压力,淬火充分,相变后出现了带有细小晶粒结构的马氏体,因而硬度大,其微观组织如 图8所示。底部和侧壁位置的微观晶粒也主要由马氏体构成,还有部分贝氏体存在,相比而言,侧壁含有较多的贝氏体,而贝氏体比马氏体的硬度低,导致材料的宏观硬度和机械强度值有所降低。

表4

Table 4

表4(Table 4)

表4 U型热成形件的机械性能试验和仿真结果对比 Table 4 Comparison between tests and simulation results for mechanical performance of U-shaped hot forming parts 位 置 试验结果 仿真结果 V1 /(℃·s-1) V2 /(℃·s-1) 硬度 /HV V1 /(℃·s-1) V2 /(℃·s-1) 硬度 /HV A 61.20 29.41 442.5 68.35 22.12 468.91 B 110.29 80.68 481.76 113.28 55.10 494.86 C 39.38 25.31 404.12 41.23 26.28 394.12 D 115.44 60.12 495.65 109.37 79.35 490.52

表4 U型热成形件的机械性能试验和仿真结果对比 Table 4 Comparison between tests and simulation results for mechanical performance of U-shaped hot forming parts

基于非等温热成形冷却速率规律,通过基础分区冷却试验,建立了高强度热成形钢硬度、强度与冷却速率之间的关系,通过数值仿真实现了热成形产品硬度、强度的机械性能预测。结果表明:随着冷却速率的增大,板料的硬度和抗拉强度逐渐增大,延伸率逐渐减小。分析二次冷却速率 V₂的影响可知,当 V₂小于20 ℃/s时,会发生显著的回火过程,热成形产品的硬度和抗拉强度也随之减小。基于量纲分析法和反推法建立了冷却速率-硬度-机械强度指数模型,通过子程序将模型引入自主开发的KMAS_HF软件模块中,采用典型的U形件进行有限元机械性能仿真预测,结果表明,所建立的冷却速率-强度-硬度指数模型具有良好的适用性和可靠性。