作者简介:欧阳丹彤(1968-),女,教授,博士生导师.研究方向:基于模型诊断,语义Web.E-mail:ouyd@jlu.edu.cn
将模型诊断引入到本体调试的局部定位,在定义公理的部件术语集的基础上给出不可满足概念的MUCS,实现在本体术语集的局部调试。利用MUCS将不可满足概念的逻辑错误定位至公理内部,MUCS调试与现有的本体调试是相互独立的。调用外部DL推理机计算不可满足概念的一个MUCS,并结合宽度优先原则和Reiter碰集树算法得到所有MUCS。最后利用现实本体对本文算法进行测试,实验结果表明:与传统的MUPS本体调试方法相比,MUCS调试方法能够将逻辑冲突定位到局部位置,准确有效地完成本体调试任务。
We introduce the model-based diagnosis into local pinpointing of ontology debugging. The concept of MUCS is given on the basis of component terminology definition to achieve the local debugging on terminology. We take the advantage of MUCS to pinpoint the logical errors of unsatisfiable concept to the axiom interior, which is independent of the existing ontology debugging. One MUCS for an unsatisfiable concept is calculated by calling an external DL reasoner, and all MUCSs are obtained by combing the principal of breath-first with hitting set theory of Reiter. Finally, the realistic ontology is used to conduct a comprehensive test of the MUCS algorithm. Experimental results show that the MUCS debugging algorithm could point out the local position of logical conflict in an axiom specifically, and efficiently and accurately complete the ontology debugging task.
公理定位是本体调试的一个重要环节,目前主要分为两类:最大可满足子术语集(A-MSSs,Maximally A-satisfiable subsets),最小不可满足保持子术语集(MUPS,Minimal unsatisfiability preserving sub-TBox)或者辩护(justification),其中辩护是比MUPS广泛的概念。关于A-MSSs,主要是Meyer[ 1]针对非展开ALC本体,提出一种基于tableau演算的方法计算最大可满足子术语集,给出相应的优化技术。关于MUPS,Schlobach[ 2, 3]提出自上而下计算不可满足概念的所有MUPS方法(针对非展开ALC本体)和自底向上计算一个MUPS方法。关于justification,Kalyanpur[ 4, 5]对同一本体中多个不可满足概念之间的关联性做了分析和研究,定义了不可满足概念的依赖,结合碰集方法只对一些特殊概念计算其辩护(等价于Schlobach提出的MUPS)。此外,Baader[ 6]证明了基于自动机的DLs推理方法可以被扩展到本体调试的定位,即一个单调布尔公式的最小值MUPS(或者辩护)对应。本体调试的另一个重点是对故障知识库的诊断。诊断是调试的一个重要部分,集中于识别导致本体不一致的公理集。Schlobach[ 7]提出了本体术语集的调试框架,以传统的模型诊断为基础[ 8, 9]。Friedrich[ 10]给出本体中诊断的一般概念,并提供正确完备的计算极小诊断的方法。Shchekotykhin[ 11]通过对目标本体进行查询确定最终的目标诊断。处理本体不一致的方法有很多,Haase和Qi[ 12]对本体调试研究进行系统性的分析和综述,得出结论:没有哪一种本体调试的方法是普遍适用于所有应用场景的,不同的方法是适合于不同调试目的和调试要求的。
Schlobach[ 2]首次提出本体调试中两个重要的概念:MUPS和MIPS。基于描述逻辑系统的调试结果是一个存在逻辑冲突的公理集,去掉或修改该结果可以使一个或者多个概念可满足,类似于命题逻辑中的极小冲突集[ 8]。本体调试的定义并不依赖某种特定的描述逻辑,MUPS和MIPS分别是概念不可满足和本体术语集不一致原因的形式化定义。
定义1(MUPS[ 2]) 设概念 C是TBox T中的不可满足概念,一个子集 T'ÍT称为关于 C的极小不可满足保持子集(MUPS),如果 C在 T'下是不可满足的,但对于任意 T″⊂ T', C在 T″下都是可满足的。
定义2(MIPS[ 2]) 设TBox T是不一致的,一个TBox T'ÍT称为 T的极小不一致保持子集(MIPS,Minimal incoherence-preserving sub-TBoxes),如果 T'是不一致的,对于任意TBox T″⊂ T', T″是一致的。
我们用 mups( T, C)表示 T中关于 C的所有MUPS的集合, mips( T)表示 T的所有MIPS的集合。例子TBox T1如下:
α1: A1⊆﹁ A∩ A2∩ A3 α4:⊆ A4⊆∀ s.B∩ C
α2: A2⊆ A∩ A4 α5: A5⊆ $s.﹁ B
α3: A3⊆ A4∩ A5 α7: A7⊆ A4∩ $s.﹁ B
α6: A6⊆ A1∪ $r.( A4∩﹁ C∩ A3)
对例子TBox T1进行调试得到:
mups(T1,A1)={{α1,α2},{α1,α3,α4,α5}}
mups(T1,A3)={{α3,α4,α5}}
mups(T1,A6)={{α1,α2,α4,α6},{α1,α3,α4,α5,α6}}
mups(T1,A7)={{α4,α7}}
mips(T1)={{α1,α2},{α3,α4,α5},{α4,α7}}
现有的本体调试是从整个本体术语集定位概念不可满足错误,概念在相应MUPS表示的术语集下是不可满足的,将错误的原因解释为:不可满足概念的定义公理与其他概念定义相矛盾。
基于模型诊断是将待诊断的系统表示成一个抽象模型,将抽象模型对系统行为的预测值与实际结果进行比较来确认故障部件。系统的部件集COMPS是一个常量集合;系统的模型用一组逻辑公式SD来描述,称为系统描述;系统的观测行为OBS是逻辑公式集合。如果观测到的系统行为与抽象系统中所有部件都正常工作得到的预测行为不一致,那么说明系统中某些部件出现了故障。Reiter[ 8]最早提出基于一致性诊断,他通过引入反常模式AB和正常模式﹁AB,将系统模型化为一个三元组(SD,COMPS,OBS)。
定义3 (SD,COMPS,OBS)的一个诊断是一个极小部件集ΔÍCOMPS使得SD∪OBS∪{AB(a)|a∈Δ}∪{AB(a)|a∈COMPS-Δ}一致。
假设诊断中的部件是故障的,并且其他部件都是正常行为模式,得到的结果与系统描述和观测是一致的。基于一致性的诊断是满足一致性的极小部件集,它的任一真子集都不是基于一致性的诊断。
定义4 (SD,COMPS,OBS)的一个冲突集是一个部件集{a1,…,ak}ÍCOMPS使得SD∪OBS∪{AB(a1),…,AB(ak)}不一致。称(SD,COMPS,OBS)的冲突集是极小的(极小冲突集)当且仅当它的任一真子集都不是(SD,COMPS,OBS)的冲突集。
Schlobach将基于模型的诊断应用到描述逻辑本体中,本体术语集是系统,公理是部件,其中基本概念和角色是输入,定义的概念是输出,最后术语集的一致性(概念的可满足性)是观测。当将概念的可满足性作为观测时,MUPS对应的极小冲突集;术语集一致性作为观测时,MIPS对应极小冲突集。MUPS和MIPS中所有公理被认为是故障部件。例子 T1对应到模型诊断系统,COMPS={α1,α2,α3,α4,α5,α6,α7};OBS={A1,A3,A6,A7}。mips(T1)是系统的所有极小冲突集,例如冲突集{α1,α2}是不一致的,其任一真子集都一致。ΔT={{α1,α4},{α2,α4},{α1,α3,α7},{α2,α3,α7},{α1,α5,α7},{α2,α5,α7}}(ΔT表示T1的所有诊断)。
在本体语境下,概念的定义方式直接影响概念的可满足性,由于公理描述中使用的概念相互矛盾,从而导致公理所定义的概念不可满足。这样,结合模型诊断,不可满足概念对应的公理被认为是故障部件,我们要解决的问题就是在本体术语集的局部(即故障部件内部)定位冲突概念。为了实现这种局部定位逻辑错误,首先需要将故障部件转换成等价的系统模型即部件术语集,二者具有相同的输入和输出,并且在相同的输入值下得到相同的输出值,然后以系统中剩余的部件为基础,在该子系统中进行局部查找极小冲突集,即MUCS。本文研究只有包含公理(概念和角色包含公理)的本体术语集,对于等价公理,需要将其转换成相应的包含公理。
部件术语集的转化规则如下:
The → 
If Γ contains C'⊆C1∩C2,but it does not contain both C'⊆C1 and C'⊆C2.
Then Γ=Γ\{C'⊆C1∩C2}∪{C'⊆C1,C'⊆C2}.
The→ 
If Γ contains C'⊆C1∪C2, and either C1 or C2 is not A,﹁A,μ.A or μ.¬A where A is an atomic concept or T and μ is $R,∀R,≥nR or ≤nR.
Then Γ=Γ\{C'⊆C1∪C2}∪{C'⊆C'1∪C'2,C'1⊆C1,C'2⊆C2} where C'1 and C'2 are new concepts not occurring in T and Γ.
The →λ-ruleR
If Γ contains C'⊆λ.D where λ is $R, ≥nR or ≤nR and n is a non-negative integer.
Condition: D is D1∩D2, then Γ=Γ\{C'⊆λ.D}∪{C'⊆λ.D',D'⊆D1,D'⊆D2};
Condition:D is D1∩D2,then Γ=Γ\{C'⊆λ.D}∪{C'⊆λ.D1⊆λ.D2};
where D' is a new concept not occurring in T and Γ.
The →∀-ruleR
If Γ contains C'⊆∀R.D.
Condition: D is D1∩D2, then Γ=Γ\{C'⊆∀R.D}∪{C'⊆∀R.D1,C'⊆∀R.D2};
Condition: D is D1∪D2 and either D1or D2 is not A,﹁A, μ.A or μ.﹁A where A is an atomic concept or T and μ is ∃R,∀R, ≥nR or ≤nR, then Γ=Γ\{C'⊆∀R.D}∪{C'⊆▯R.(D1'∪D2'), D1'⊆D1, D2'⊆D2};
where D1' and D2' are new concepts not occurring in T and T.
给定TBox T,αC是T中概念C的定义公理,假设αC的右边概念是否定标准形式(¬只出现在原子概念的前边)。为了计算αC对应的术语集,该算法由TBox Γ={αC}开始,对Γ应用规则,直到没有规则可用时终止,称最后得到的Γ为αC的部件术语集(Component terminology)。
结论1 设α是TBox T中概念C的定义公理,Γ是把转换规则应用于{α}得到的术语集,那么,C基于T\{α}∪Γ是不可满足,的当且仅当C在T下不可满足。
我们将公理α的部件术语集记作Γα,同样地,内部的每条公理是系统Γα的一个部件。根据部件术语集的计算规则,不难知道α的模型也是Γα的模型,同时α的模型可以通过扩展Γα的模型得到。另外,按照给出的规则,可以得到唯一确定的公理的部件术语集。
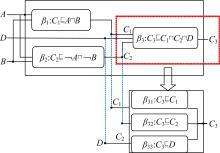
图1中,上边部分是TBox T={ β1, β2, β3}对应的系统(输入为基本概念 A和 B),观测为 T不一致,并且 C3是不可满足的,对 T进行诊断得到 M={ β1, β2, β3}是系统 T的极小冲突集;下边部分 Γ={ β31, β32,
例子TBox T1中 α1和 α6的部件术语集分别为 Γα1 ={ A1⊆ ¬A, A1⊆ A2, A1⊆ A3}, Γα6 ={ A6⊆ A1∪ X1, X1⊆ $r.X2, X2⊆ A4, X2⊆ ¬C, X2⊆ A3}。
在故障部件对应的子系统(部件术语集)中对概念的不可满足进行诊断,从而将概念不可满足的逻辑错误定位至公理的内部。
定义5(MUCS) 设概念 C是TBox T中的不可满足概念, Γα是 C的定义公理 α的部件术语集。一个子集 Γ⊆ Γα称为 T中 C的极小不可满足部件子术语集(MUCS,Minimal unsatisfiability component sub-TBox),如果 C在 T\{ α}∪ Γ下是不可满足的,并且对于任意 Γ'∩ T, C在 T\{ α}∪ Γ'下都是可满足的。
我们用 mucs( T, C)表示 T中关于 C的所有MUCS的集合。例子TBox T1中各不可满足概念的所有MUCS如下:
mucs( T1, A1) ={{ A1⊆﹁ A, A1⊆ A2},{ A1⊆ A3}};
mucs( T1, A3) ={{ A3⊆ A4, A3⊆ A5}};
mucs( T1, A6) ={{ A6⊆ A1, A6⊆ X1, X1⊆ $r.X2, X2⊆ A4, A1⊆﹁ C},{ A6⊆ A1, A6⊆ X1, X1⊆ $r.X2, X2⊆ A3}};
mucs( T1, A7) ={{ A7⊆∃ s.B, A7⊆ A4}}。
MUCS与MUPS二者并不矛盾,MUCS可以看做是MUPS的补充,实现在公理表示的部件术语集内部查找局部冲突集。MUCS的任意真子集都不是极小的不可满足部件子术语集,其中的公理都是使得概念不可满足的必要定义公理。这样,移除MUCS中任意一条公理,都会达到消解MUCS对应的逻辑错误。
本节给出计算不可满足概念单个MUCS的黑盒方法,进一步地结合Retiter的碰集自上而下地计算所有MUCS。算法与DL推理机相互独立,需要推理机提供概念在相应的本体下可满足性测试结果,而推理机内部的具体实现对算法是不可见的。通过调用外部DL推理机,实现对任意基于DL语言的本体进行调试。其中,如果概念不止一条定义公理,那么,将合并每条定义公理的部件术语集,合并结果作为概念的定义公理的部件术语集。
Algorithm SINGLE_MUCS(T,C,Sc)
Input: TBox T, Concept C, subset of component terminology of Cs axioms Sc
Output: set of axioms M
M ← Æ
T1←Sc∪(T-{αc|αc is the axiom of C in T})
if C is satisfiable w.r.t T1,then
return Æ
for each axiom α∈Sc,do
T1←T1-{α}
if C is satisfiable w.r.t T1,then
M←M∪{α}
T1←T1∪{α}
return M
SINGLE_MUCS算法实现求解TBox T中不可满足概念 C在公理集 T'∪ Sc下的一个MUCS,其中 Sc是 C的定义公理的部件子术语集(部件术语集的子集), T'为 T除去 C的定义公理之后的本体术语集。如果 C在 T'∪ Sc是可满足的,返回值为空;否则,逐个处理 Sc中的公理。删除 Sc中的公理 α之后,若 C仍是不可满足的,说明删除的公理不影响 C在 T'∪ Sc中的可满足性, α不是 C的不可满足的逻辑错误;若 C是可满足的,则 α是 C的逻辑错误原因,将其保存到 M中,同时将 α恢复到本体中,其中 M是最后的返回结果。
定理1 C是TBox T中一个不可满足概念,如果 C在 T'∪ Sc下是不可满足的,那么SINGLE_MUCS( T, C, Sc)∈ mucs( T, C),其中 Sc是 C的定义公理的部件子术语集, T'为 T除去 C的定义公理之后的本体术语集。
证明 TBox T中不可满足概念 C在 T'∪ Sc下是不可满足的,SINGLE_MUCS算法中变量 M就是 C的一个MUCS。循环处理 Sc中公理之前设 Sc={ α1,…, αm}。 ①首先, C在 T'∪ M下是不可满足的。本体逐个删除 Sc中公理 αi(1≤ i≤ m),如果 C可满足,则将所删除公理恢复到本体同时保存到 M中,否则不做任何操作。这样,删除 αi之前, C在当前本体 T'∪ M∪{ αi,…, αm}下是不可满足的,处理完 Sc中所有公理之后, C在 T∪ M下是不可满足的。 ②任意 M'⊂ M, C在 T'∪ M'下是可满足的。假设存在 M'⊂ M使得 C在 T'∪ M'下不可满足,令 Dc=M-M',那么对任意 M″⊂ M'都有 C在 T'∪ M″下是不可满足的。处理完 Sc-Dc中所有公理时有 C在 T'∪ M'∪ Dc是不可满足的,当处理 Dc中的公理时都有 C是不可满足的,最后得到的 M=M',这与 M'⊂ M矛盾,假设不成立。证毕。
定理1保证了SINGLE_MUCS算法的正确性和完备性,算法中进行概念可满足性测试与输入参数中部件子术语集 Sc的大小有关,如果 Sc有 n个元素,则最多需要进行 n+1概念可满足性测试。
MUCS_HST是计算不可满足概念所有MUCS的一种黑盒算法,该算法利用Reiter的碰集树方法,对SINGLE_MUCS算法得到的单个MUCS进行展开,进而得到概念其他的MUCS。下面首先给出碰集和碰集树的定义。
定义6(碰集[ 8]) 设 F是一个集合簇, F的碰集(hitting set)是一个集合 H⊆∪ s∈ FS,使得对所有 S∈ F, H∩ S≠ Æ。称 F的一个碰集为极小的当且仅当它的任何一个真子集都不是 F的碰集。
定义7(碰集树,HS-tree[ 8]) 设 F是一个集合簇,一个对结点和边做了标记的树 Tr称作是 F的碰集树(HS-tree)当且仅当 Tr满足下列性质:
(1)如果 F为空,则根结点标识为 '√ ';否则,生成作为树根的结点,结点标识为 F中的一个元素。
(2)设 n是 Tr的一个结点,处理结点 n:
①定义 P( n)为从根结点到 n路径上边标识的集合;
②若存在集合 S∈ F使得 S∩ P( n) =Æ,则 n被标识为 S即 L( n) =S,否则,标识为'√';
③若 n被标识为 '√ ',则 n没有后继结点;
④若 n被标识为集合簇 F的一个集合 Σ,则对每一个 δ∈ Σ, n有一个后继结点 m与 n通过一条边 e=<n, m>相连,边 e的标识为 δ即 L( e) =δ;
如果 n是一个标识为 '√ '的结点,那么 P( n)是 F的一个碰集。 F的每一个极小碰集都是HS-tree中某标识为'√'的结点 n的 P( n)。标识为 '√ '的结点 n的 P( n)并不包含 F的所有碰集,但包含了 F的所有极小碰集。访问 F的意思是为了选择此树中结点的标识所进行的计算,这种选择结点 n的标识的计算是在 F中搜索满足 S∩ P( n) =Æ的集合 S。如果 S被找到,结点 n被标识为 S,否则它被标识为'√'。本文MUCS_HST算法中, F是不可满足概念的所有MUCS,但是 F不是显式地可以获得的,一次对 F的访问需要调用SINGLE_MUCS计算 F的一个MUCS。为了产生一棵尽量小、只给出 F的极小碰集、访问 F次数最少的HS-tree,在BUILD_HST算法生成碰集树的过程中:①采用宽度优先来扩展结点;②关闭规则:如果结点 n已被标识为 '√ ',且新结点 n'满足: P( n) ÍP( n'),那么可以关闭 n'( L( n) ='×')不对 n'继续扩展; ③重用结点规则:设结点 n被∑标识出( Σ={ δ,…}),若碰集树中存在 n',使得 L( n')∩( P( n)∪{ δ}) =Æ,那么让 n下的 δ-弧指向这个已经存在的 n',不需要再扩展 n',否则调用SINGLE_MUCS产生新结点并对新结点进行扩展。
MUCS_HST算法中,变量 HS保存碰集, F保存得到的MUCS。算法首先为构造的碰集树提供一个根结点 r,并将 r加入到队列QUEUE中,然后逐个扩展QUEUE中结点。这样,以队列的方式实现宽度优先遍历,对每个结点进行完全展开生成碰集树。碰集树中除了标识为'√'和'×'的结点,剩余的结点都是相应不可满足概念的MUCS,并且是所有的MUCS。
定理2 C是TBox T中一个不可满足概念, α是 C在 T中的定义公理, Tc =T\{ α}∪Γ α。 C基于 T'⊂ Tc是可满足的当且仅当 H=Tc -T'是 mucs( Tc, C)的一个碰集, H是 mucs( Tc, C)的极小碰集当且仅当对任意 H'⊂ H, C基于 Tc -H'是不可满足的。
定理3 如果 Tr是MUCS_HST( T, C)算法生成的碰集树,那么下列两个命题等价:
(1)令 N( Tr)为碰集树 Tr中所有标识为 '√ '的叶结点 n的集合, M( T)为 mucs( T, C)所有极小碰集的集合,那么 ∪n∈N(Tr) P( n) =M( T);
(2)MUCS_HST( T, C)= mucs( T, C);
定理2和3的正确性都可以根据Reiter的碰集树理论得到证明,这里证明略。
MUCS_HST( TC)算法如下
Algorithm MUCS_HST(T,C)
Input:TBox T, Concept C
Output:set of axiom sets S
get the defining axiom α of C in T
Sc←Tα
T' ←T \ {α}∪Sc
m ← SINGLE_MUCS(T', C, Sc)
create a node r and set L(r) ← m
HS ← Æ
F ← {m}
QUEUE ← {r}
while QUEUE is not empty, do
N ← get the head element of QUEUE
for each axiom β∈L(N), do
create a new node N' and set L(N')←Æ
create a new edge e=<N, N'> with L(e)←β
if there exists a set hÎHS s.t. hÍP(N)∪{β},then
L(N') ←'×'
else if there exists a set k∈F s.t. k∩(P(N)∪{β})=Æ,
then
L(N')←k
QUEUE←QUEUE+N'
else
Ac←Sc-P(N)-{β}
m ←SINGLE_MUCS(T, C, Ac)
if m = Æ, then
L(N')←'√'
HS←HS∪{P(N)∪{β}}
then
L(N') ←m
F ← F∪{m}
QUEUE ←QUEUE + N'
return F
本文实验是在PC机win7操作系统(Intel(R) Core(TM)i5-3470 CPU @3.20 GHz,8.00 GB的内存)下运行,前边描述的算法都用java语言实现,调用pellet推理机判断概念的可满足性。通过实验说明计算不可满足概念的MUCS实现本体调试的可行性,基本测试方法是用现实本体检测调试方法性能。由于现实中可用的不一致本体术语集有限,本文采用Koala本体和DICE本体的一个片段对本文调试方法进行评估。MadCow是ALCH(D)本体,包括53个概念1个不可满足概念和41条公理,本文方法所需时间为15 ms;DICE是ALCH本体,其中包含527个概念、76个不可满足概念和505条公理,本文方法所需时间为23.151 s。
Case 1:mad+cow是MadCow本体中一个不可满足概念.
α1: mad+cow⊆cow∩$eats.(brain ∩$part+of.sheep)
α2: cow⊆vegetarian
α3: vegetarian ⊆∀eats.∀part+of.﹁ animal∩ animal ∩∀eats.﹁ animal
α4: sheep ⊆∀eats.grass∩ animal
mups(MadCow, mad+cow)={{α1,α2,α3,α4}}
mucs(MadCow,mad+cow)={mad+cow⊆cow,mad+cow⊆X1, X1⊆$eats.X2,X2⊆$part+of.sheep}
Case 2:B292是DICE本体中一个不可满足概念.
β1: B292 ⊆C151∩L12∩…(其中,省略号部分表示有近百个原子概念否定的合取)
β2: C151⊆Z141∩…
β3: L12 ⊆﹁ Z141∩…
mups(DICE, B292)={{β1,β2,β3}}
mucs(DICE, B292)={{B292⊆C151, B292⊆L12}}
MUCS能够正确地给出概念不可满足的逻辑错误。MadCow本体中,mad+cow只有一个MUCS即{mad+cow⊆cow,mad+cow⊆X1,X1⊆$eats.X2,X2⊆$part+of.sheep},说明mad+cow的不可满足错误是由于cow与$eats.$part+of.sheep同时定义mad+cow,从而发生矛盾引起的。消去新增的概念X1和X2,得到cow的定义与$eats. $part+of.sheep冲突。这样,MUCS直接将mad+cow的错误定位到$eats.$part+of.sheep,排除$eats.brain。所以,MUCS可以更精确地在公理的内部找到概念不可满足原因的位置。DICE本体中,有一部分不可满足概念的定义公理类似Case 2中的B292的定义形式,每个不可满足概念的定义公理较大(公理中合取构造符的数量为公理的长度)。这种情况下,相较于MUPS,MUCS能更加详细地给出逻辑不一致的原因。
实验证明利用MUCS进行本体调试的可行性,MUCS与MUPS是相互独立的,互不影响,得到的调试结果都能在不同程度上指出本体不一致的位置。不可满足概念的定义公理规模越大,MUCS_HST算法的执行时间越长。
通过对公理进行规则变换得到对应的部件术语集,在此基础上定义不可满足概念的MUCS,MUCS将不可满足概念的逻辑错误更具体地定位到概念定义公理的局部。文中所提出的利用Reiter碰集树方法计算不可满足概念所有MUCS的MUCS_HST算法较好地实现了这一想法。在实验评测环节,采用现实本体对MUCS_HST算法进行实验测试:测试结果表明利用MUCS将不一致本体的逻辑错误定位到公理的局部是可行的,与求解MUPS的现有本体调试相互独立并不冲突;另外,概念的定义公理直接影响算法的执行时间。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|