基于局部二进制描述SIFT特征的锆石图像配准方法

引用本文

邱春玲, 陶强, 范润龙, 王培智. 基于局部二进制描述SIFT特征的锆石图像配准方法. 44(6): 1793-1798
QIU Chun-ling, TAO Qiang, FAN Run-long, WANG Pei-zhi. Zircon image matching method based on description of SIFT feature by LBP. Journal of Jilin University Engineering and Technology Edition, 44(6): 1793-1798 复制到剪切板

Permissions

基于局部二进制描述SIFT特征的锆石图像配准方法

邱春玲¹, 陶强¹, 范润龙², 王培智¹

1.吉林大学仪器科学与电气工程学院,长春 130022

2.中国地质科学院地质研究所,北京 100037

通信作者:范润龙(1980-),男,助理研究员.研究方向:质谱仪器控制,大型科学仪器远程控制.E-mail:fanrunlong2003@126.com

作者简介:邱春玲(1963-),女,教授.研究方向:分布式测控,分析仪器.E-mail:qiuchunling@jlu.edu.cn

基金:国家重大科学仪器开发专项项目(2011YQ050069,2011YQ05006907);

摘要

针对尺度不变特征变换(SIFT)算法计算复杂度高、匹配速度慢的问题,提出一种新的局部二进制模式(LBP)特征描述方法,描述SIFT算法检测出的锆石图像特征点,然后用主成分分析法(PCA)将生成的描述向量降维,最后利用欧式距离法完成配准。新LBP描述方法计算简单,具有旋转不变性和光照不变性,描述向量经过PCA降维以后匹配过程简单快速。实验结果表明:配准效果可以满足仪器自动寻样的需求,并且能够显著提升锆石图像的配准速度、提高仪器运行效率。

关键词: 计算机应用; 图像配准; SIFT算法; 局部二进制模式; 主成分分析

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2014)06-1793-06

Zircon image matching method based on description of SIFT feature by LBP

QIU Chun-ling¹, TAO Qiang¹, FAN Run-long², WANG Pei-zhi¹

1.College of Instrumentation & Electrical Engineering, Jilin University, Changchun 130022,China

2.Institute of Geology Chinese Academy of Geological Sciences, Beijing 100037, China

Abstract

In order to solve the problem of high computational complexity and low matching speed of the traditional Scale Invariant Feature Transform (SIFT) algorithm, a new method of feature description using Local Binary Patterns (LBPs) was proposed. This method was used to describe the zircon image feature points detected by SIFT algorithm. The dimensionality of the feature vector was reduced using Principal Component Analysis (PCA), and the descriptor matching was carried out with Euclid Distance. The new description method of LBPs has a more simple calculation, and this algorithm has excellent features of rotation invariance and illumination invariance. The descriptor matching is faster after PCA dimension reduction. Experimental results show that this method meets the requirements of automated sample search, and significantly improves the matching speed of zircon images, improves the efficiency of the instrument.

Keyword: computer application; image matching; SIFT algorithm; local binary patterns; principal component analysis(PCA)

Show Figures

锆石微区定年技术是地质年代学领域中应用最广的技术方法。高分辨二次离子探针质谱仪(SHRIMP II)在锆石微区年龄测定方面有无可替代的优势,为实现该仪器的自动寻样,提高仪器的运行效率,需要为仪器采集的锆石图像的准确配准设计一种快速、适用的算法。

尺度不变特征变换(Scale invariant feature transform,SIFT)算法是由Lowe教授^{[ 1, 2]}提出的,是目前应用最广的特征检测图像匹配方法之一。算法内容可以分成3个部分:①特征点检测;②特征点的描述,生成特征向量;③特征向量匹配。SIFT算法虽然最终的配准点对众多,然而其特征点的描述过程过于复杂,导致整个配准过程时间过长,文中应用不需要过多的配准点对,而且其较低的匹配效率更加不利于仪器的自动化。Heikkil等^{[ 3]}提出了一种CS-LBP算法来描述特征区域,并将其与SIFT算法结合,减少了特征描述时间,但是生成的特征向量维度由SIFT的128维变成了256维,导致特征匹配复杂度增加,最终的配准效率也是改善甚微。文献[4]提出用成分分析(Principal component analysis,PCA)方法对SIFT特征向量降维,但由于其采用了更大的特征邻域构建描述符,又抵消了降维所带来的速度提高。

本文在SIFT算法提取的特征点基础上,提出并采用一种新的局部二进制描述算子描述特征点15×15领域,减小了原算法的描述复杂度,简化了特征点的描述,然后用PCA方法对描述生成的特征向量降维,最后配准。在保证配准率满足仪器自动化的前提下,缩短了配准时间,明显提高了仪器运行效率。

1 SIFT特征点的检测

检测图像的SIFT特征点就是寻找图像的尺度空间的极值点。一幅图像 I( x, y)的尺度空间图像表示为:

$\begin{matrix} \begin{matrix} D (x, y, σ) = \\ (G (x, y, kσ) - G (x, y, σ)) * I (x, y) = \\ L (x, y, kσ) - L (x, y, σ) (1) \\ 式中 : \\ L (x, y, σ) = G (x, y, σ) * I (x, y) (2) \end{matrix} \end{matrix}$

G( x, y, σ)为二维高斯函数:

$\begin{matrix} G (x, y, σ) = \frac{1}{2 π σ^{2}} e^{- (x^{2} + y^{2} \frac{)}{2} σ^{2}} (3) \end{matrix}$

σ为尺度空间因子,也是高斯函数的方差,其值越小图像被平滑得越少,尺度就越小;符号“*”表示卷积运算。为了有效地在尺度空间检测到极值点,用金字塔形式构建图像的尺度空间,图像金字塔共有 O组,每组有 S层,每层是原图像对应于尺度 σ( O, S)的尺度空间图像,下一组图像由上一组图像降采样得到,尺度 σ( O, S)表示如下:

$\begin{matrix} σ (O, S) = σ_{0} 2^{(O + S) / S} (4) \end{matrix}$

式中: O、 S分别为高斯图像所在的组数和层数。算法中 O、 S、 σ₀的取值分别为7,6,1.6×2^1/3。

构建完图像的尺度空间金字塔以后,对金字塔中的每个点进行比较,即将每个点与同一尺度的周围邻域8个像素和相邻尺度对应位置的周围邻域9×2个像素总共26个像素进行比较。当该点像素值比所有邻域像素值都大或都小时,该点为极值点。极值点的检测是在离散空间中进行的,检测到的极值点并不是真正意义上的极值点,因此通过函数拟合方法精确定位极值点的位置和尺度,同时去除响应值小和不稳定的边缘响应点。在极值点对应尺度空间邻域内采样,用直方图统计邻域内的梯度方向,将0~360°等分为36份,即每10°一个柱,直方图的峰值代表了该极值点的方向 θ。这样就确定了极值点的位置、尺度和方向。

2 SIFT特征点的局部二进制描述

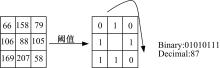
图1给出了一个基本的LBP描述算子。对于一个像素点,以该点的灰度值作为阈值,将其周围3×3的9邻域的像素灰度值与其进行比较,比它大的为1,比它小的为0,按照一定的顺序将二值化的结果组成一个8位二进制数,以此二进制数的值(0~255)作为该点的LBP响应。本文在基本LBP描述算子基础上提出了一种新的描述算子AVG-LBP。

	Figure Option View Download New Window
	图1 基本LBP算子Fig.1 Basic LBP operator

2.1 AVG-LBP描述算子

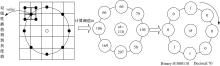
新的描述算子AVG-LBP选取待描述点半径为2的圆形邻域内的8个像素点,如图2所示,图中一个方格对应一个像素,对于正好处于方格中心的邻域点(左,上,右,下四个黑点),直接以该点所在的方格像素值作为它的值;不在方格中心的点(斜45°方向的4个黑点),用双线性插值法确定其像素值,假设该点像素值为 value,邻近4个像素点为 I( i-2, j-2), I( i-2, j-1), I( i-1, j-2), I( i-1, j-1),则由双线性插值法可求得 value值表达式如下:

$\begin{matrix} \begin{matrix} value (1) = I (i - 2, j - 2) + \\ 0.5858 * (I (i - 2, j - 1) - I (i - 2, j - 2)), \\ value (2) = I (i - 1, j - 2) + \\ 0.5858 * (I (i - 1, j - 1) - I (i - 1, j - 2)), \\ value = value (1) + 0.5858 * \\ (value (2) - value (1)) (5) \end{matrix} \end{matrix}$

在计算待描述点的LBP值时,本文使用该点圆形邻域内8个点的平均值作为新的阈值,新的LBP算子为:

$\begin{matrix} \begin{matrix} AVG - LBP = \overset{8}{\sum_{i = 1}} s (ni - m) 2^{i - 1}, \\ s (x) = \{\begin{matrix} 1, x > 0 \\ 0, x \leq 0 \end{matrix}, m = (\overset{8}{\sum_{i = 1}} ni) / 8 (6) \end{matrix} \end{matrix}$

式中: m表示圆形领域内8个点的平均值, n_i表示圆形领域内的8个点的像素值。

如图2所示,与图1中8个邻域像素值相同,新的LBP算子 AVG-LBP=70,而基本 LBP=87。通过实验结果可知,改进后的LBP描述算子有效地抑制了噪声的影响。

	Figure Option View Download New Window
	图2 AVG-LBP算子Fig.2 AVG-LBP operator

2.2 特征点的AVG-LBP描述

根据第1节检测到的SIFT特征点,可以得到特征点所在的尺度 σ、方向 θ和坐标( x_i, y_i)。由尺度 σ得到对应的尺度空间图像 I( x, y, σ),在尺度空间 I( x, y, σ)上取特征点坐标周围19×19大小的描述区域,进行如下步骤的处理,对应的图像和直方图如图3所示。

	Figure Option View Download New Window
	图3 AVG-LBP描述Fig.3 AVG-LBP descriptor

(1)将19×19大小的描述区域旋转 θ角度至特征点的主方向,确保描述区域的旋转不变。

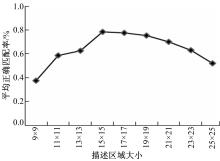
(2)取旋转后区域内特征点周围15×15大小的区域作为最后的LBP描述区域,一共225个点,描述区域大小确定为15×15的原因在本文后续章节中有介绍。

(3)对15×15个像素点求 AVG-LBP值,得到225个在0到255范围内的值,将此225个值保存为直方图向量 HistLBP。

(4)为了消除光照的影响,对直方图向量 HistLBP进行归一化处理,即:

$\begin{matrix} HistLBP'_{i} = \frac{HistLB P_{i}}{\sqrt[]{\sum HistLB P_{i}^{2}}} (7) \end{matrix}$

并将归一化后 HistLBP的阈值设为0.2,大于0.2的值直接取值为0.2。最后得到256维的特征向量 HistLBP。

3 特征向量的主成分分析方法降维

PCA的实质是在尽可能准确地代表原始数据的前提下,通过线性变换将高维空间中样本数据投影到低维空间中。由AVG-LBP算子描述的特征向量是256维,如图3(d)所示,存在降维的空间。将检测出的 k个特征点对应的 k个256维特征向量组成 k×256大小的二维矩阵 D,将其与事先计算的256 ×n维投影矩阵相乘,得到 k×n大小的降维后的二维特征矩阵,本文 n为20。因此需要得到256×20大小的投影矩阵。

PCA降维方法其实就是求投影矩阵的过程,本文按如下步骤生成投影矩阵:

(1)对一系列同类的锆石图像提取特征点,一共 m个特征点,将所有特征点的特征向量组成 m×256大小的二维矩阵 A。

(2)计算矩阵 A的协方差矩阵cov A,该矩阵大小为256×256。协方差矩阵的计算公式为:

$\begin{matrix} A = A - mean (A), covA = A^{T} A (8) \end{matrix}$

式中:mean( A)表示求矩阵 A的均值。

(3)计算协方差矩阵cov A的特征值和对应的特征向量,取前 n个特征向量,本文中 n取20,得到256 ×20大小的投影矩阵 P。投影矩阵只需计算一次,并存储,降维时只需做一个矩阵的乘法运算 D×P。

当两幅图像的AVG-LBP特征向量生成后,采用特征向量的欧式距离作为两幅图像中特征点的相似性判断度量。取图像A中某个关键点,找出其与图像B中欧式距离最短的前两个关键点,如果最近的距离乘以某个比例阈值 threshold小于次近的距离,则接受最近的这一对匹配点。提高比例阈值 threshold,匹配点有减少,但会更加稳定,准确率更高。两个向量( n₁, n₂, n₃,…, n_i)和( m₁, m₂, m₃,…, m_i)的欧式距离公式为:

$\begin{matrix} d = \sqrt[]{(n_{1} - m_{1})^{2} + (n_{2} - m_{2})^{2} + \dots + (n_{i} - m_{i})^{2}} (9) \end{matrix}$

4 实验及分析

本文对SIFT做了两个改变,首先用AVG-LBP区域描述代替SIFT的梯度直方图描述,然后对描述向量做PCA降维后再配准。实验分别将两个改变后的配准效果与SIFT算法的配准效果进行比较和分析,最后对3个算法的配准时间进行比较。之前需要做如下两个工作:

首先,如2.2节中所描述的,用特征点周围领域15×15的范围作为AVG-LBP的描述区域,15×15大小的范围是通过反复实验确定的,正如图4所示,并不是描述区域越大配准率越高,相反描述区域太大会影响配准速度,因此本文选择15×15大小的描述区域。

	Figure Option View Download New Window
	图4 特征点AVG-LBP描述区域Fig.4 AVG-LBP description region of the keypoint

然后,需要选择一批同类型的图像来求取PCA降维时所需要的投影矩阵,因为本文算法的应用方向是高分辨二次离子质谱仪器中采集的锆石图像,所以事先从仪器中采集大量同类型的锆石图像,并按照第3节中的步骤进行投影矩阵 P的计算。图5是本文所选择的部分实验图像。

	Figure Option View Download New Window
	图5 投影矩阵的计算图像Fig.5 Text images of computing projection matrix

4.1 配准效果分析

为了检验新的配准算法的配准效果和实用性,将本文对SIFT算法进行的两次改变分别与原SIFT算法进行比较。测试图像来自高分辨二次离子质谱仪器SHRIMP II;SIFT算法选择加利福尼亚大学Andrea Vedaldi博士提供的算法Matlab环境下的算法源码;本文算法是在SIFT算法代码框架基础上进行编写的,先用LBP特征描述符代替梯度描述符,取名PCA-LBP-SIFT算法,再在PCA-LBP-SIFT算法的基础上增加PCA降维,最终的锆石图像快速配准算法取名PCA-LBP-SIFT算法。

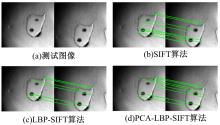
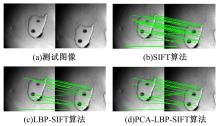	Figure Option View Download New Window
	图6 锆石测试图像和相同阈值条件下三种算法的配准效果Fig.6 Zircon test image and the matching result of the three algorithms in the same threshold

评价基于关键点的配准算法的常用方法是计算配准率,即正确配准点数/总配准点数。如第3.2节中所叙述的,改变阈值 threshold可以改变两幅图像的总配准点数,首先在 threshold=2时,比较3种算法的配准率。如图6所示,SIFT算法的配准率为34/38=89.4%,LBP-SIFT算法的配准率为22/25=88.0%,PCA-LBP-SIFT算法的配准率为23/28=82.1%。可以看出,LBP-SIFT算法配准率和SIFT算法差别不大,但是总的匹配点数下降明显,而PCA-LBP-SIFT算法相对于LBP-SIFT算法配准率有所下降,但是总的匹配点数有所增加。总体上,新算法的配准效果有所下降,但是鉴于新算法的研究目的在于计算出两幅图像的偏移量,用以进行样品台的坐标校正,所以通过改变阈值 threshold,使最终的配准效果中没有错配点(没有交叉对),然后对所有配准点坐标的偏移量求平均值,得到图像的偏移量,实验方法如下。

选择两个测试图像对,一对是只含有一个锆石颗粒的样品图像,如图7(a)所示;一对是含有多个锆石颗粒的样品图像,如图8(a)所示。用这两对图像基本可以代表这一类锆石图像。分别用3个算法对两对图像进行匹配,同时调整 threshold值,使配准结果中没有误配点。如图7和图8所示,测试图像1中,原SIFT算法最终的匹配点对数为11个,LBP-SIFT算法为8个,PCA-LBP-SIFT算法为9个;测试图像2中,原SIFT算法最终的匹配点对数为12个,LBP-SIFT算法为7个,PCA-LBP-SIFT算法为8个。从实验结果可以看出,新的算法得到的正确匹配点对数相比原SIFT算法稍有下降,另外,对LBP-SIFT算法做PCA降维后,配准点对数反而有所增加,新算法可以得到至少5个以上的配准点对。

	Figure Option View Download New Window
	图7 锆石测试图像1和没有误配点时3种算法的配准效果Fig.7 Zircon test image No.1 and the matching result of the three algorithms without incorrect matching points

	Figure Option View Download New Window
	图8 锆石测试图像2和没有误配点时3种算法的配准效果Fig.8 Zircon test image No.2 and the matching result of the three algorithms without incorrect matching points

4.2 算法速度比较

文中算法的特征点检测部分与SIFT算法一致,所以只对特征点的描述向量生成和描述向量的匹配两部分做比较。实验测试机器配置:操作系统Windows7 32位专业版;处理器Intel i7 3.4 GHz;内存4.0 GB;程序运行环境Matlab 2010;测试图像是1280 pix×1024 pix的锆石样品图像。测试结果如表1所示。新算法的描述时间比原SIFT算法减少了近一半,经过PCA降维以后的特征向量描述时间也由0.07 s降到0.002 s。最终,新算法的锆石图像配准时间在1 s左右。以下为理论分析。

表1 特征点描述和匹配时间对比 Table 1 Comparison of the interest points description and matching

(1)特征点的描述:SIFT算法中使用基于梯度方向直方图的特征描述方法,为了得到梯度方向和幅值,如式(10)(11)所示,需要进行开根号和反三角函数操作,运算复杂度高。

梯度幅值:

$\begin{matrix} \begin{matrix} m (x, y) = \\ \sqrt[]{[L (x + 1, y) - L {(x - 1, y)]}^{2} + [L (x, y + 1) - L {(x, y - 1)]}^{2}} (10) \\ 梯度方向 : \\ θ (x, y) = ta n^{- 1} [\frac{L (x, y + 1) - L (x, y - 1)}{L (x + 1, y) - L (x - 1, y)}] (11) \end{matrix} \end{matrix}$

然而,在LBP-SIFT算法和PCA-LBP-SIFT算法中,用AVG-LBP算子描述特征点,只进行简单的减法运算,计算速度提升显著。

(2)特征点的描述向量匹配:SIFT算法、LBP-SIFT算法、PCA-LBP-SIFT算法的描述向量分别是128维、256维和20维,都是通过计算欧式距离进行配准,而且NEWLBP描述的特征向量数据复杂度比梯度法描述的要低,所以新算法的匹配时间也会缩短。因此,本文算法配准时间显著减少。

5 结束语

在SIFT算法的基础上,提出了一种基于局部二进制的特征点描述方法,并且利用PCA对描述向量进行降维,在保持原算法对光照、旋转、尺度变化的鲁棒性的同时,解决了原算法计算复杂度高、配准时间长的问题。实验结果表明:新算法的特征描述时间降至原算法的一半,降维后的描述向量配准时间缩短至2 ms;并且算法成功地应用在高分辨二次离子质谱仪的锆石图像配准上,提高了仪器的工作效率。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Lowe D G. Object recognition from local scale-invariant features[C]∥The Proceedings of the Seventh IEEE International Conference on Computer Vision, Indian, 1999: 1150-1157. [本文引用:1]
[2]	Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. [本文引用:1] [JCR: 3.623]
[3]	Heikkil M, Pietikinen M, Schmid C. Description of interest regions with local binary patterns[J]. Pattern Recognition, 2009, 42(3): 425-436. [本文引用:1] [JCR: 2.632]
[4]	Ke Y, Sukthankar R. PCA-SIFT: a more distinctive representation for local image descriptors[C]∥Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Japan, 2004: 506-513. [本文引用:1]
[5]	Juan L, Gwun O. A comparison of sift, pca-sift and surf[J]. International Journal of Image Processing, 2009, 3(4): 143-152. [本文引用:1]
[6]	Zhang J, Zhang K, Niu W, et al. SAR image automatic registration based on PCA-SIFT and Mahalanobis distance[C]∥Proceedings of the International Conference on Information Engineering and Applications, London, 2013: 445-452. [本文引用:1]
[7]	Guo Z, Zhang L, Zhang D. A completed modeling of local binary pattern operator for texture classification[J]. IEEE Transactions on Image Processing, 2010, 19(6): 1657-1663. [本文引用:1] [JCR: 3.199]
[8]	Abdi H, Williams L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews: Computational Statistics, 2010, 2(4): 433-459. [本文引用:1]
[9]	李根, 李文辉. 基于尺度不变特征变换的平面旋转人脸检测[J]. 吉林大学学报: 工学版, 2013, 43(1): 186-191. Li Gen, Li Wen-hui. Face detection under rotation in image plane based on scale invariant feature transform[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(1): 186-191. [本文引用:1] [CJCR: 0.701]
[10]	Ahonen T, Hadid A, Pietikainen M. Face description with local binary patterns: Application to face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(12): 2037-2041. [本文引用:1] [JCR: 4.795]

1999

0.0

2004

3.623

0.0

. 2004, 60(2):91-110 DOI:10.1023/B:VISI.0000029664.99615.94

Distinctive image features from scale-invariant keypoints

1.University of British Columbia<br/>

This paper presents a method for extracting distinctive invariant features from images that can be used to perform reliable matching between different views of an object or scene. The features are invariant to image scale and rotation, and are shown to provide robust matching across a substantial range of affine distortion, change in 3D viewpoint, addition of noise, and change in illumination. The features are highly distinctive, in the sense that a single feature can be correctly matched with high probability against a large database of features from many images. This paper also describes an approach to using these features for object recognition. The recognition proceeds by matching individual features to a database of features from known objects using a fast nearest-neighbor algorithm, followed by a Hough transform to identify clusters belonging to a single object, and finally performing verification through least-squares solution for consistent pose parameters. This approach to recognition can robustly identify objects among clutter and occlusion while achieving near real-time performance.

2009

2.632

0.0

. 2009, 42(3):425-436 DOI:10.1016/j.patcog.2008.08.014

Description of interest regions with local binary patterns

Abstract

This paper presents a novel method for interest region description. We adopted the idea that the appearance of an interest region can be well characterized by the distribution of its local features. The most well-known descriptor built on this idea is the SIFT descriptor that uses gradient as the local feature. Thus far, existing texture features are not widely utilized in the context of region description. In this paper, we introduce a new texture feature called center-symmetric local binary pattern (CS-LBP) that is a modified version of the well-known local binary pattern (LBP) feature. To combine the strengths of the SIFT and LBP, we use the CS-LBP as the local feature in the SIFT algorithm. The resulting descriptor is called the CS-LBP descriptor. In the matching and object category classification experiments, our descriptor performs favorably compared to the SIFT. Furthermore, the CS-LBP descriptor is computationally simpler than the SIFT.

... Heikkil等^[3]提出了一种CS-LBP算法来描述特征区域,并将其与SIFT算法结合,减少了特征描述时间,但是生成的特征向量维度由SIFT的128维变成了256维,导致特征匹配复杂度增加,最终的配准效率也是改善甚微 ...

2004

0.0

2009

0.0

2013

0.0

2010

3.199

0.0

2010

0.0

. 2010, 2(4):433-459 DOI:10.1016/j.apor.2010.09.005

Principal component analysis

Abstract

The new artificial intelligence models proposed for the preliminary design of rubble mound breakwaters consist of (1) multi layer feed forward artificial neural networks, (2) hybrid artificial neural networks with principal component analysis, (3) fuzzy systems, and (4) fuzzy neural networks. These models are applied for the stability analyses of Mersin yacht harbor main breakwater, as a case study in Turkey. A better agreement between the predicted stability numbers of hybrid artificial neural networks and measurements is obtained when compared to the stability equations. The Hybrid Artificial Neural Network model that is trained by the pre-processed database of measurements obtained from the Principal Component Analysis is considered as a robust technique in handling uncertainties inherent in the preliminary design. The fuzzy system and fuzzy neural network models have the advantages of incorporating flexible reasoning as expert systems when compared to hybrid neural networks; however, they require the development of new prediction enhancement techniques for the improvement of their forecasts.

2013

0.0

0.701

. 2013, 43(1):186-191

Face detection under rotation in image plane based on scale invariant feature transform

College of Computer Science and Technology, Jilin University, Changchun 130022, China

To solve the problem of face detection under rotation in image plane, an improved Scale Invariant Feature Transform (SIFT) algorithm is proposed. With the invariant properties of rotation, scale, translation and illustration, the SIFT algorithm is used to detect the rotation face in image plane. First, a pruning algorithm, combining the template and contrast, is used to increase the efficiency and filter the invalid key points; and a higher accuracy main direction algorithm is proposed. Then, the AdaBoost algorithm is used to train a common face classifier and compute the matching ratio of key points. Finally, the SIFT algorithm detects the face under rotation in image plane, and normalizes the face by the main direction of key points. Experiment results indicate that improved algorithm preserves the high detection ratio, and performs better in normalization precision and detection efficiency.

针对平面旋转人脸检测的问题,改进了传统的尺度不变特征变换(SIFT)算法,利用其旋转、缩放、平移及部分仿射不变性完成平面旋转人脸的检测。首先通过模板与对比度加权的方法对SIFT关键点进行裁减,以提高计算效率并过滤无效关键点,然后提出一种更精确的主方向计算方法确定关键点主方向,通过Adaboost算法训练人脸公共特征分类器并计算关键点的匹配率作为置信权值,完成平面旋转人脸的检测,并根据关键点主方向进行扶正。最后通过实验与传统方法进行了对比,结果表明:本文方法在保证检测率的同时,在扶正精确度、检测速度方面均有较大提高。

2006

4.795

0.0