以交通调度为目的的交通监控系统,除了对特定车辆的监控外,更加关注道路网上车辆聚集信息的获取,如每个路段上交通流量、平均速度等信息。道路网上的信息是以数据流的形式存在的,如果对每条信息都进行存储和处理,存储空间需求巨大。即使能存储这么多数据,对如此庞大的数据进行处理也需要很大的时间开销,将无法满足智能交通系统对路网进行实时监控、调度的要求,所以对道路网上的数据流进行聚集查询一般采用近似处理技术,属于时空数据库中移动对象的聚集查询范畴,如查询下班高峰期17时到18时期间,某一路段有多少辆车通过,以分析该时段该路段上的交通拥挤情况,从而适当地调整该路口的交通信号灯或为驾驶员提供实时导航,来减轻交通拥挤情况。研究者提出了许多移动对象时空间聚集索引法,比较典型的有:aRB-tree^{[ 1]}、Sketch^{[ 2, 3]}、AMH^{[ 4]}。aRB-tree索引结构存在重复计数问题^{[ 5]};Sketch索引结构利用草图之间的OR运算解决了重复计数问题,但是该索引结构仅适用于欧氏二维空间;AMH通过智能划分空间,将道路网上非均匀分布的移动对象划分到不同的桶中,使每个桶内的移动对象分布均匀,解决了移动对象的非均匀分布问题,但仍存在重复计数问题。两个改进版本AMH^{*[ 6]}和AMH^{+[ 7]}具有低空间复杂度、高查询质量的优点。DS^{[ 8]}索引结构利用AMH^{*[ 6]}技术对Sketch^{[ 5]}进行划分,并且结合具有路网特性的Sketch-RR-tree^{[ 6]}索引结构。但是DS索引结构未考虑路网方向问题,且AMH^*添加的对桶的约束条件限制较严格,数据存储的开销较大。DS索引结构只支持count查询,无法对average等其他类型进行近似聚集查询。虽然也有索引结构^{[ 9, 10]}考虑了对象的轨迹、方向等,但这些结构是基于整个网络的,而不是基于某个区域路段,而且不能很好地支持聚集查询。

本文采用AMH^{+[ 7]}技术智能划分结合了Sketch技术的支持方向属性聚集的aCN-RB-tree^{[ 11]},提出了一种考虑方向的路网移动对象时空间聚集索引结构DSD+(DynSketch+with Directions),并将其应用于路网上以支持 sum( q_T, q_R)(时间区域为 q_T,空间区域为 q_R的车辆数之和)和 avg( q_T, q_R)(时间区域为 q_T,空间区域为 q_R的平均车辆数)两种桶的数据聚集查询。

DSD+索引结构首先将空间划分为2 n×n个部分,并将所有栅格划分为若干桶,桶内的数据分布均匀,当有数据分布发生变化时,则以特定的约束条件^{[ 6]}来分裂或合并桶,从而提高查询质量。在将栅格划分为若干桶时,由于希望数据分布相近的栅格能划分在一个桶中,因此,本文针对路段建立一个BPT(Binary partition tree)树,数据以多维直方图方式保存和处理,对于某路段 rid两个方向的数据分别存放在划分空间的如下位置上:

( ridL/( n*2), ridL%( n*2))

( ridR/( n*2), ridR%( n*2))

任一桶 b_k可以表示为一个七元向量( R, n_k, f_k, g_k, v_k, hn_k, s_kt), R代表矩形范围,以桶的左下角和右上角坐标表示; n_k为 R矩形范围中对象的数目; f_k为该桶内各个栅格的平均频度, f_k=(1 /n_k)∑_{∀ c∈ R}F_c; g_k为该桶内各个栅格频度的平均平方和, g_k=(1 /n_k)∑_{∀ c∈ R} Fc2; v_k为方差, v_k=(1 /n_k)∑_{∀ c∈ R}( F_c-f_k)²,可以看出, v_k可以直接根据 f_k和 g_k求得,即 v_k=g_k-f_k²; hn_k为该桶内通过合适草图计算出的采用的草图张数; s_kt为时刻 t对应的BPT树中桶 b_k对应的草图信息, n_k就是通过草图信息由FM_PCSA算法计算得到的近似值。

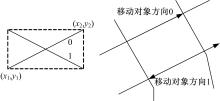
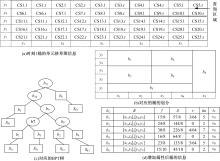
对于一个路段的 dn方向属性,假定其值域为{0,1}。如 图1所示,本文对于 dn的取值这样定义:对于某个路段,如果移动对象从最左边进入,则 dn取值为0;如果对象从最右边进入,则 dn取值为1。特殊情况,当这个路段是垂直路段时,若对象从底部进入,则 dn取0;若从顶部进入则取1。为了对双向聚集值进行索引,本文针对两个方向的车辆情况创建多维直方图结构。在时间戳1,DSD+索引结构如 图2所示, 图2(a)给出的是对每个栅格内的车辆进行草图化后的草图信息CS i,而不像AMH⁺结构那样,直接存储的是该栅格内车辆的实际数量。然后根据FM_PCSA算法计算出各个栅格的近似车辆数,将车辆数相近的栅格划分在一个桶中,如 图2(b)所示,每个桶都有一些附加的统计信息,如 图2(d)所示,也就是前面提到的七元向量。 图2(c)是对应的BPT树,在计算某个时刻某桶内车辆近似数时,不是简单地进行求和运算,而是采用Sketch思想进行草图的或运算,以此解决重复计数问题,提高查询精度。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 路段方向标识图Fig.1 Direction identifies of road segment

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 DSD+索引结构Fig.2 Structure of DSD+

图2(c)中的BPT树用以索引 图2(b)中的桶,与AMH⁺不同的是其叶子节点存储的是每个桶的草图信息,在构建带有方向属性的BPT树的过程中,初始仅仅包含一个叶子节点,整个空间区域就是一个大的桶,然后根据桶的约束条件,决定是否要进行桶的分裂或者合并,在建立索引结构时,BPT树上叶子节点上的草图信息并不单独为其分配空间,而将其作为一项属性保存在 图2(d)桶的信息中。

DSD+索引结构的聚集查询算法能通过 direction属性值查找受限路网中路段某个特定方向的聚集值,更符合实际路网中的应用需求。

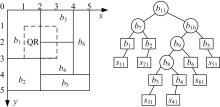
如 图3所示,桶中的虚线框为查询区域,该桶存储的是所有路段 direction=0方向的草图信息,查询的时间段为[1,2],查询区域如 图3所示,右边为时间戳为1时,增加草图信息后的BPT树结构。查询时给出( x_min, x_max, y_min, y_max, t_max, dn),前4个给出的是虚线框查询区域的边界点坐标,接下来是查询的时间段,最后一个为查询的方向,以便在正确的BPT树上进行查找。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 DSD+索引结构查询举例Fig.3 Example of query based on DSD+

查找时,直接从根节点开始中序遍历查找,图中从根节点 b₁₁开始,由于它为中间节点,且其分裂标识为 y_flag=2,而查询区域为(1,3,1,3),分裂标识在其区域内,因此, b₁₁的左右子树都需要访问,根据中序遍历的非递归算法,先将 b₁₁存储在栈中,然后访问它的左子树,左子树处理完后, b₁₁再出栈,处理它的右子树。处理左子树时,由于 b₇也是中间节点,但是其分裂标识为 x_flag=3,因此,查询区域在 b₇的左子树,也就是 b₁,而 b₁为叶子节点,求出桶 b₁与查询区域QR的相交部分的面积,设为 R1,同时对当前查询到的桶进行时刻1和时刻2对应草图的OR运算,得到 s₁,即 s₁ =s₁₁ OR s₁₂,根据FM_PCSA算法求出在时间戳1和时间戳2范围内,去除重复计数后的车辆数聚集结果,设为 num1,同时根据桶的平均频率计算出与查询区域相交的车辆数量为 f₁ ×R₁ /n₁,接着 b₁₁出栈,遍历其右子树,用同样的方法找到与QR相交的叶子节点 b₃和 b₄,分别求出其与QR相交部分的面积 R3和 R4,以及对应桶两个时间戳草图信息的或运算,即 s₃ =s₃₁ OR s₃₂和 s₄ =s₄₁ OR s₄₂,再根据FM_PCSA计算出它们去除重复计数后的车辆数,分别记为 num3和 num4,与查询区域相交区域的车辆数分别为 f₃ ×R₃ /n₃和 f₄ ×R₄ /n₄,最后将所有草图进行或运算得到 s=s₁ OR s₃ OR s₄,根据FM_PCSA计算出其近似估计车辆数为 N。

遍历结束后,怎样整合出最终查询结果是本文要研究的问题,显然,不能直接将与查询区域相交部分的车辆数直接相加,得到 allnumber=f₁ ×R₁ /n₁ +f₃ ×R₃ /n₃ +f₄ ×R₄ /n₄,而不同的桶所采用的草图张数也可能不一样,因此也不能直接将草图进行OR运算来解决重复计数问题,本文采用的是在 allnumber基础上减去所有与查询区域相交部分的平均重复计数的车辆数,记为( n₁ +n₃ +n₄ -N) ×( R₁ +R₃ +R₄) /( R_b1 +R_b3 +R_b4),最终,针对 图3的查询结果为 allnumber-( n₁ +n₃ +n₄ -N) ×( R₁ +R₃ +R₄) /( R_b1 +R_b3 +R_b4),换言之,聚集查询的结果是在基本的求和得到的 allnumber基础上减去一个平均重复计数。

试验采用Geographic Data Technology Inc 1999年采集的美国加利福尼亚州公共交通路网数据,地图比例为1∶24000,路网的平均密度为1451 路段/km²。首先截取784个路段,然后采用浮动车技术模拟生成10000辆车,车有car、bus、truck和autobike四种类型,这些车以不同的车速匀速行驶,数据流的格式为< tm, rid, eid>,即时间、路段号、车辆标识,每隔10秒记录这些信息,共记录180个时刻的车辆信息。本部分试验都是在Windows XP操作系统上实现的,系统配置为1.5 G内存,AMD 2.0 GHz,开发环境为VC++6.0,开发语言为C++。

试验采用FM_PCSA算法对移动车辆进行草图化,每个桶中采用的草图数目不一样,草图张数是通过文献[12]中的合适草图的方法解决。查询范围依据文献[13]中的 r_r=3, t_t=5,也就是说查询空间范围为3×3个路段,时间范围跨度为5个时刻。DS将784个路段划分为28×28栅格,而DSD+划分为28×28×2栅格,首先不考虑路段上车辆信息的方向属性。

3.1 DSD+和DS查询性能对比

3.1.1 DSD+和DS索引查询时间比较

作为一个服从正态分布的随机变量 ρ=1 /( d t),当 ρ≥0 .95时,可以认为这一事件为高概率事件,在某种意义上可以称之为必然事件,根据 ρ和 η( ρ)之间的对应关系,当 ρ=0 .95时, η( ρ)对应的值为1.96,在本文后面的试验中, η( ρ)取值1.96。 ε暂且设置为3。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 DS和DSD+不同设置时查询时间比较Fig.4 Query time comparison between DS and DSD+ while different set

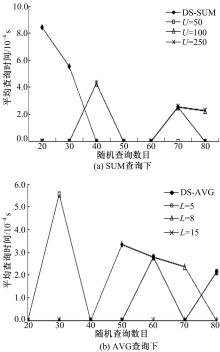
图4比较了DS和DSD+分别以 sum( q_T, q_R)和 avg( q_T, q_R)查询下桶的约束条件为case1: v_b≤( εsum2) /( η²( ρ) n²)和 v_b≤( εsum2) /( η²( ρ) U),以及case2: v_b≤ (εavg/η(ρ))2和 v_b≤ L· (εavg/η(ρ))2时,对于以10为步长的20~80个随机查询的平均查询时间。图中case1代表的是针对 ε_sum=3时,DS和DSD+的 U参数分别设置为50、100、250的比较;case2代表的是 ε_avg=3时,DS和DSD+的 L参数分别设置为5、8、15的比较, L和 U是DSD+的查询上下限参数,即[ L, U]⊆[1, n²],其中 n为栅格的分辨率,即路网被划分为 n×n个栅格。

从 图4中可以看出:DSD+和DS结构在时间方面有一样的优势,都不到1 ms,大多数情况下几乎为0,近似查询的速度很快。

3.1.2 随机产生查询的平均相对误差分析

图5针对sum( q_T, q_R)与avg( q_T, q_R)两种查询的桶约束条件,比较了DS与DS⁺以10为步长随机生成20~80个查询的平均相对误差。

图5

Fig.5

	Figure Option ViewDownloadNew Window
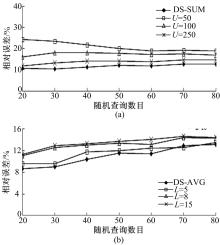	图5 DS和DSD+随机产生查询的平均相对误差比较Fig.5 Average relative error comparison between DS and DSD+ while generate queries randomly

从 图5可以看出:对于DSD+来说,平均相对误差都与 U值成反比,而与 L值成正比, U=50和 U=100时,平均相对误差较大。 L=5时,平均相对误差较小,因此,接下来,试验将DSD+参数设置为 L=5,并与DS比较,从图中可以看出DS的平均相对误差要比DSD+的小,但是相差不大,平均误差都在10%左右。

3.1.3 DSD+和DS索引存储空间分析

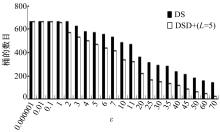
通过上面的分析可知,虽然DS和DSD+两者查询的误差都能保证在一定的范围内,但是DSD+桶的数目要少得多,从桶的约束条件上也是可以看出的,DS中的AMH*对桶的限制较为严格,致使生成的桶的数目过大,而DSD+中AMH⁺通过参数 L和 U可以调节约束条件,并且保证误差在一定范围内。 图6给出了 ε设置不同值时,DS和DSD+( L=5)各自需要的桶的数目,其中,随机查询数目设置为60,查询区域不变。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 ε设置不同值时所需的桶数目Fig.6 Number of barrels required while different ε

从 图6可以看出: ε越小,需要的桶的数目越多,一般情况下,桶的数目越大,查询的精度越高,但是存储空间越大,而在 ε≥1之后,DSD+所需的桶数目比DS所需的要少得多,而 图5显示两者的精度差不多,换言之,DSD+可以更好地权衡存储空间与查询精度之间的利弊,DSD+所需的桶数目更少,查询精度上也有一定的保证,随着数据量的增大,DSD+在空间存储上的优势将更加明显,且空间存储减少后,查询时间效率上也必将明显优于DS索引。

试验还分析了 ε取值对相对误差的影响,并进行了Sketch生成时间及草图大小的对比,鉴于论文篇幅所限,试验对比结果不一一给出。结合 图6中 ε和桶的数目之间的关系可知,当 ε=5时,不仅精度能有保证,而且桶的数目小得多,从而减少了空间存储及查询时间。同时桶的数目减少了,相应的草图生成时间以及草图的存储空间也减少了。

3.2 考虑方向属性的DSD+性能分析

本部分试验加入方向属性考查DSD+性能。将路段划分为( RES×2) ×RES个栅格,每个路段 rid占据两个栅格,分别对应路段的两个方向,由于总共784个路段,因此试验中 RES取28。以往关于路网数据流聚集查询技术的研究,对于随机产生的60个查询是对每个实际车辆数大于0的路段都加入到平均相对误差计算中,然而实际应用中,用户可能更关心哪些路段拥堵,因此,本文只针对实际车辆数大于5的路段进行试验研究,以考查DSD+的性能。

3.2.1 ε对DSD+查询精度的影响分析

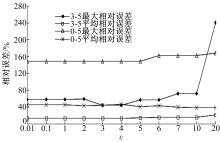
根据 图5,选择精度较好的 L=5的情况进行试验,查询范围首先定为 r_r=3, t_t=5,由于需要支持单个方向车辆数的查询,实验室设置 r_r=0代表的是查询某个路段单一方向的车辆数,若 y坐标是偶数表示 direction=0方向; y为奇数表示的是 direction=1方向,为了使得对单一方向的查询精度更高,在选择恰当的 ε时,不仅考虑 r_r=3, t_t=5的情况,还要考虑 r_r=0, t_t=5时查询的相对误差。 图7是分别针对3-5和0-5两种查询,将 ε从0.01变化至20,观察两种查询的最大相对误差以及平均相对误差。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 ε对DSD+查询精度的影响Fig.7 Effect on the query accuracy of DSD+ about ε

从 图7可知: ε=3时两种查询的最大相对误差及平均相对误差较小,查询效果较好。

3.2.2 r_r对DSD+查询精度的影响分析

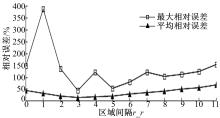
图8描述了选择效果较好的 ε=3, t_t=5, r_r从0变化至11,0代表随机产生的某个路段单个方向上的车辆数,DSD+( L=5)索引查询的最大相对误差及平均相对误差,由于总路段数为28×28×2=1568,也就是说查询范围是从总路段数的1/1568到121/1568,换算成百分比就是总区域的0.0638%到7.7168%。从 图8可以看出:在时间间隔为5(每个时间间隔为10 s)的条件下,区域间隔为3时,查询效果最好;区域间隔大于8时,不管是最大相对误差还是平均相对误差都呈上升趋势,只有区域间隔为3时,误差最小,可见,DSD+索引结构较适用于这一范围内的查询。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 不同区域间隔相对误差的比较Fig.8 Relative error comparison while different regional intervals

3.2.3 t_t对DSD+查询精度的影响分析

图9描述了区域范围固定为3,也就是查询覆盖范围为9个路段, ε和 L的值与前面保持一致,时间间隔 t_t从1变化到10,DSD+( L=5)索引查询的最大及平均相对误差。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 不同时间间隔相对误差的比较Fig.9 Relative error comparison while different time intervals

从 图9可以看出:查询时间间隔为1~3时,最大相对误差都较大,时间间隔较长的相对误差都较小,这也比较符合现实生活中,较长时间的车辆流动信息更能真实反映查询区域的交通状况,本试验中,间隔时间为5和6时,平均相对误差和最大相对误差都最小。

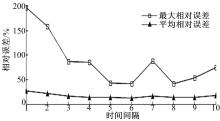
3.2.4 DSD+单向聚集查询性能分析DSD+借鉴了aCN-RB-tree的双向聚集属性,因此本文将对单向聚集查询性能进行分析。 图10为 ε=3, L=5, r_r=0, r=0 .95(即 h( r) =1 .96),时间间隔 t_t从1变化到10时,DSD+对单一方向车辆数的聚集查询相对误差。

图10

Fig.10

	Figure Option ViewDownloadNew Window
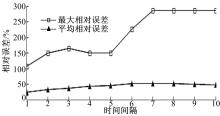	图10 不同时间间隔路段单个方向查询相对误差Fig.10 Single direction of road segment query relative error while different time intervals

从 图10可以看出:时间间隔为1~5时的DSD+的最大相对误差及平均相对误差要较小,而时间间隔为1~10时的平均相对误差都在50%左右,时间间隔为1时的平均相对误差最小为23.842698%。而由 图8可知:区域间隔为3时,平均相对误差的最小值为13.244223%,单一路段车辆数较少,在较短时间间隔内误差较小,而随着时间变长,误差逐渐增加,直到一定时刻保持平稳。而 r_r=3时,包含9个路段,18个栅格,车的数量较多,近似查询精度较高。虽然DSD+对于单一方向的近似查询精度没有跨越多个区域的查询精度高,但是它在近似聚集技术中考虑了方向属性的查询,更符合实际中路段的双向性。

采用AMH⁺技术智能划分结合Sketch技术的支持方向属性聚集特性的aCN-RB-tree,提出了DSD+索引结构,并将其应用于路网上的移动对象聚集查询。试验结果表明:该方法在保证查询时间、平均相对误差的前提下,可以更好地权衡存储空间与查询精度之间的利弊,同时考虑了实际路段的双向性。