传统的指纹拓扑结构只提取脊线特征,或只提取邻域特征。王业琳等^{[ 4]}通过提取纹线特征,进行指纹纹线相似度的匹配。王伟希等^{[ 5]}以中心点为圆心,提取中心点周围的方向场进行匹配,属于提取邻域特征。这两类方法的误识率和拒识率均较高,因此本文将脊线特征、邻域特征和细节点特征相结合,设计了新的拓扑结构。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 指纹特征点标定Fig.1 Calibration of fingerprint feature points

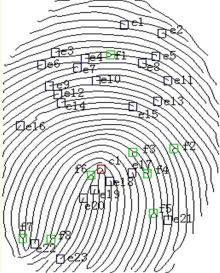
指纹的特征点有叉点和端点。如 图1所示,该图片标定了该指纹图像上的所有叉点,端点和中心点,叉点标号为 f1, f2,…, f8;端点标号为 e1, e2,…, e23;中心点标号为 c1。(绿方格代表叉点;蓝方格代表端点;红方格代表中心点)

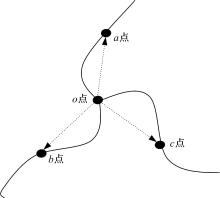
叉点相比于端点而言,信息量大且可靠,不易受非线性形变的影响,因此,首先对叉点 o的3个分支进行脊线跟踪,如 图2所示,沿3个分支各追踪 N个像素找到3个脊线点 a、 b、 c。记录脊线点和叉点的方向角度差 α、 β、 γ,提取相应叉点与3个脊线点的长度 oa、 ob、 oc,存入特征向量。叉点的坐标记作( x, y),特征点的类型中, E代表端点, F代表叉点,所得到的叉点的特征向量为{( x, y), F,( α, oa),( β, ob),( γ, oc)}。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 叉点拓扑结构Fig.2 Topology of fork point

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 端点拓扑结构Fig.3 Topology of end point

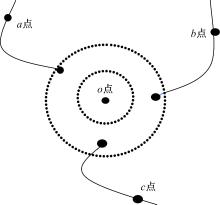
端点由于只在一条脊线上,邻域特征和脊线特征均较少,因此 k近邻法作为脊线追踪法的补充,可以进一步提取邻域特征和脊线特征。如 图3所示,首先对叉点 o利用 k近邻法找到距离较近且在环形域内的3个脊线点作为邻域特征点,然后再对脊线点所在脊线进行 N个像素的脊线追踪,找到最终的脊线点 a、 b、 c。环形域的半径依次为 R¹和 R²。将相应的脊线点与端点的方向角度差 α、 β、 γ以及长度 oa、 ob、 oc存入特征向量。端点的坐标记作( x, y),特征点的类型中, E代表端点, F代表叉点,所得到的端点的特征向量为{( x, y), E,( α, oa),( β, ob),( γ, oc)}。

在极坐标下进行特征点匹配比直角坐标更有优势,因为极坐标可以更好地描述非线性形变对指纹的影响,而且不用考虑输入指纹图片与模板指纹图片之间特征点的平移,只需要考虑它们的旋转即可,因此本文采用极坐标进行指纹匹配。

转换过程:首先选取中心点,或三角点,或第一个满足阈值的特征点作为对应的参考点( x^o, y^o),以此点建立坐标系,实现{( x, y), α}到{ ρ, θ, r}的转换,转换公式如下:

ρθr=(x-xo)2+(y-yo)2arctany-yox-xoα-αo1

式中:( x, y)为坐标; α为角度; ρ为极径; θ为极角; r为角度差。

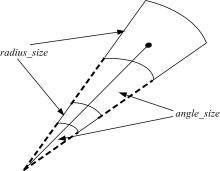
由于指纹特征点对不可能完全重合,在方向和位置上通常会存在偏差,因此引入限界盒^{[ 5]},如 图4所示,从而有效地解决了非线性形变问题,实现了一定限度的误差容忍度。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 限界盒Fig.4 Bounding box

传统的固定限界盒极径和极角均是不可变化的,虽然时间效率高,但是拒识率和误识率也较高,而全可变限界盒(即极径和极角均可变化),虽然拒识率和误识率很低,但是时间效率很差。本文借鉴二者的优缺点,将限界盒的极角设为固定值,成为半可变限界盒,相对于传统的固定限界盒和全可变限界盒,该限界盒的匹配速度较快,拒识率和误识率较低。大多数的图像增强算法是将半个圆周划分为八个方向,再进行方向角的提取^{[ 6]},由于方向角量化过程中已经实现了一定范围的鲁棒性,允许特征点方向上有一定的误差,因此将限界盒的宽度 angle_size设为固定值,不影响匹配的拒识率和误识率^{[ 7]}。半可变限界盒高度 radius_size的计算公式如下:

radius_size=r_small,r_size<r_smallr_size,r_small<r_size<r_larger_large,r_size>r_large2r_size=ρm+r_small3

式中: r_small、 r_large分别为半可变限界盒高度的上、下限; m为先设定的常数。

本文根据特征的可靠性不同,为指纹特征分配不同的权值^{[ 8]},以增加指纹匹配的准确性,分配结果如 表1所示。

表1

Table 1

表1(Table 1)

表1 特征向量的权值分配体系 Table 1 Weight distribution system of feature vector 特征点类型 距离 角度 总值 端点 2 3 15 叉点 2 3 15

表1 特征向量的权值分配体系 Table 1 Weight distribution system of feature vector

由于在指纹图像质量下降的情况下,叉点与端点之间是会发生相互转化的,因此不同类型的特征点不一定不匹配。但是特征点类型(叉点和端点)不易受非线性形变影响,所占比例较少,因此在对类型不同的特征点对进行匹配时,匹配阈值的设定较类型相同的特征点更高。

将叉点和端点的特征向量中的各个分量与 表1中所对应的权值相乘,得到匹配分数,将加权后的匹配分数与阈值相比较,若大于或等于阈值,就表明两点匹配。大量试验结果表明:类型相同的特征点对,将其匹配阈值 NUM设为9;类型不同的特征点对,将其匹配阈值 NUM设为12,匹配效果较好。