AF-MIMO系统机会中继选择算法

引用本文

陈健, 李佳龙, 阔永红. AF-MIMO系统机会中继选择算法. 44(6): 1818-1824
CHEN Jian, LI Jia-long, KUO Yong-hong. Opportunistic relay selection algorithm for AF-MIMO system. Journal of Jilin University Engineering and Technology Edition, 44(6): 1818-1824 复制到剪切板

Permissions

AF-MIMO系统机会中继选择算法

陈健, 李佳龙, 阔永红

西安电子科技大学通信工程学院, 西安 710071

作者简介:陈健(1968-),男,教授,博士生导师.研究方向:无线通信与信号处理.E-mail:jianchen@mail.xidian.edu.cn

基金:国家自然科学基金项目(60972072, 61340033); 高等学校学科创新引智计划项目(B08038);

摘要

在没有直传链路的AF-MIMO协作通信系统中,针对节点发送功率和转发功率未知情况下的最佳中继选择问题,提出了一种机会中继选择算法。该算法通过理论分析和数学推导,分别研究了协作中继数目和系统各部分的功率分配对信道容量的影响,并依据瞬时信道信息推导出简易判别式,利用最大-最小化准则选择出最佳中继,在没有增大算法复杂度的同时提升了系统信道容量。仿真结果表明,该算法选择出的最佳中继在信道容量性能方面较已有算法有一定提高,验证了所提选择算法的有效性。

关键词: 通信技术; 机会中继选择; 信道容量; 瞬时信道信息; 协作通信

中图分类号:TN929.5 文献标志码:A 文章编号:1671-5497(2014)06-1818-07

Opportunistic relay selection algorithm for AF-MIMO system

CHEN Jian, LI Jia-long, KUO Yong-hong

School of Telecommunications Engineering, Xidian University, Xi'an 710071, China

Abstract

Under the condition that transmission power and relay power of the nodes are unknown, an opportunistic relay selection algorithm is proposed to solve the problem of best relay selection in AF-MIMO cooperative communication system without direction link. By theoretical analysis and mathematical derivation, the effects of the number of cooperative relays and the power allocation in each part of the system on the channel capacity are investigated. A simple criterion is derived using the instantaneous channel state information and the best relay is selected in terms of the maximin criterion, which improves the overall channel capacity without increasing the computation complexity. Simulation results show that, the relays selected using the proposed algorithm can significantly improve the channel capacity, ahich confirms the effectiveness of the proposed algorithm.

Keyword: communication; opportunistic relay selection; channel capacity; instantaneous channel state information; cooperative communication

Show Figures

0 引言

MIMO(Multiple-input multiple-output)技术是无线通信领域的研究热点,在一定的带宽和传输功率的情况下,它通过分集增益使系统获得更大的吞吐量,从而提升通信质量^{[ 1, 2]}。随着通信技术的发展,在许多场景仅仅依靠直传链路已经不能满足通信需求,即单跳通信在衰落等情况下很难保障用户的通信质量。中继协作通信技术可以很好地对抗衰落,解决因衰落等情况导致的通信中断问题。协作MIMO系统是协作通信技术与MIMO技术的结合,它适用于长距离、大衰落的传输,在系统没有直传链路的情况下保证通信的正常进行^{[ 3, 4]}。

在协作MIMO系统中,协作中继的工作方式分为单一中继模式和混合中继模式两种。两种情况下协作中继节点的合理选取对系统信道容量均有着直接的影响。最佳中继(Very important relays,VIRs)选择算法的主要思想可以分为补充法和剔除法,即利用信道瞬时状态CSI(Channel state information),通过直接选择和间接排除的方式得出最佳协作中继节点。文献[5]提出了两种AF(Amplify-and-forward)机会中继选择策略,在已知源节点发送功率和中继节点转发功率的情况下,利用循环迭代的方式逐一选择出最优的中继节点,适用于备选中继节点数目很多的情况。文献[6]研究了基于平衡信道容量前提下的中继选择问题,采用剔除法的思想设计了最佳中继选择算法。这种算法在每次循环选择的时候需要的参数较多,算法复杂度较高。文献[7]提出了一种MIMO天线的快速选择方案,通过获取最大信道容量增量的思想筛选出最佳中继。

目前已有的中继选择算法基本是在已知节点发送功率、转发功率和信道CSI等信息的条件下进行的,而在不能完整获取节点功率信息的情况下,中继选择将无法进行。

基于上述问题,本文在MIMO系统场景下,利用协作通信技术构建了单向中继的AF-MIMO两跳通信系统。并以此系统为基础,设计了一种机会中继选择算法。该算法是在节点功率信息未知的情况下,利用获取的信道CSI信息,通过信道容量公式得出的简易判别式,对候选中继节点进行补充式筛选,得到最佳协作中继集合。

1 系统模型

1.1 AF-MIMO系统

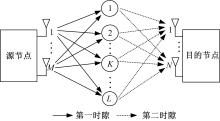
在AF-MIMO系统中^{[ 8, 9, 10]},假设源节点有 M个天线,目的节点有 N个天线和 K个中继节点,每个中继节点只有一个天线,即组成半双工两跳的协作通信系统。如图1所示,假设源节点和目的节点之间没有直传链路^{[ 5, 6]},所有的通信都要通过中继节点的转发来协作完成。中继采用AF传输模式,选择方式为机会中继,即根据信道瞬时状态CSI来选择。信道CSI的获取依靠训练序列来完成:首先,源节点发送训练序列给中继节点,以探明源节点-中继节点的信道情况;然后,中继节点发送训练序列给目的节点,以探明中继节点-目的节点的信道情况;最后,中继节点广播源-中继节点信道情况给所有节点。假设所有信道为瑞利衰落信道,在一次选择中保持不变。源节点到中继节点的信道 H_s_, _r和中继节点到目的节点的信道 G_r_, _d是独立同分布的,每两个节点间的信道增益均服从均值为0、方差为 σ²的复高斯随机变量。同时根据RTS/CTS(Request to send/clear to send)机制,各个中继节点知道自身的信道状态。

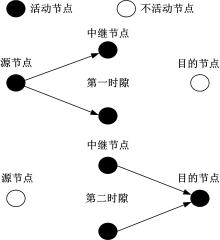
	Figure Option View Download New Window
	图1 系统模型Fig.1 System model

中继采用半双工工作方式,所以协作通信分两个时隙来完成。假设协作中继节点的集合为 r=[ r(1),…, r( L)],则源节点到中继节点的信道和中继节点到目的节点的信道分别为 H_L= $\begin{matrix} [{h^{T}}_{r (1)}, \dots, {h^{T}}_{r (L)}]^{T} \end{matrix}$ 和 G_L=[ g_r₍₁₎,…, g_r₍ _L₎]。第一时隙,源节点发送信号到中继节点;第二时隙,协作中继节点对信号直接放大并转发,经过信道 g_r₍ _k₎到达目的节点。双时隙工作过程如图2所示。

	Figure Option View Download New Window
	图2 半双工工作过程Fig.2 Semiduplex process

1.2 信道容量分析

假设源节点的总发送功率为 P_s,且满足 $\begin{matrix} \sum_{{k-1_{}}_{}}^{L_{}} \end{matrix}$

P_k=P_s,协作中继节点的总转发功率为 P_r,且满足 $\begin{matrix} \sum_{{k-1_{}}_{}}^{L_{}} P r, k \end{matrix}$ =P_r。在信号传输的第一时隙,系统采用迫零波束赋形技术(Zero-forcing beamforming,ZFBF)。定义第 k个协作中继的ZFBF因子为 w_k=w'_k/‖ w'_k‖, k=1,…, L,满足‖ w_k‖₂ =1且 h_r₍ _j₎ w_k=0,( j≠ k);其中‖·‖₂为矩阵的二范数, w'_k为矩阵 H'_L= $\begin{matrix} {H^{H}}_{L} \end{matrix} \begin{matrix} (H_{L} {H^{H}}_{L})^{- 1} \end{matrix}$ 的第 k列。

设定发送信号矢量为 x= $\begin{matrix} [x_{1}, \dots, x_{L}]^{T} \end{matrix}$ ,且满足 E $\begin{matrix} \{x x^{H}\} \end{matrix}$ =I_L。源节点发送信号 s可以写成 s= $\begin{matrix} \sum_{{k-1_{}}_{}}^{L_{}} \begin{matrix} \sqrt[]{P_{k}} \end{matrix} w k x k \end{matrix}$ 。经过第一时隙的信道传输之后,到达第 k个中继节点的接收信号为:

$\begin{matrix} y_{r (k)} = \sqrt[]{P_{k}} h_{r (k)} w_{k} x_{k} + n_{1, k} (1) \end{matrix}$

通过AF中继放大之后的信号为:

$\begin{matrix} f_{k} = a_{k} y_{r (k)} (2) \end{matrix}$

其中放大因子为:

$\begin{matrix} a_{k} = \sqrt[]{\frac{P_{r, k}}{P_{k} ‖ h_{r (k)} w_{k} ‖^{2} + σ_{n}^{2}}} (3) \end{matrix}$

式中:‖·‖表示矩阵的Frobenius范数。

L个协作中继节点在接收到源节点发送的信号之后,同时对放大后的信号进行转发,经过第二时隙的传输到达目的节点。在目的节点处采用迫零(ZF)检测接收技术来估计 x_k, k=1,…, L。设第 k个迫零检测因子为 v_k=v'_k/‖ v'_k‖, k=1,…, L,同样满足 $\begin{matrix} ‖ v_{k} ‖_{2} \end{matrix}$ =1且 $\begin{matrix} {v^{H}}_{k} \end{matrix}$ g_r₍ _j₎ =0,( j≠ k),其中 v'_k表示的是矩阵 G'_L= $\begin{matrix} ({G^{H}}_{L} G_{L})^{- 1} \end{matrix} \begin{matrix} {G^{H}}_{L} \end{matrix}$ 的第 k行。则经过第 k个中继协作传输到达目的节点并经过迫零检测的接收信号为:

$\begin{matrix} \begin{matrix} z_{k} = {v^{H}}_{k} (\overset{L}{\sum_{k = 1}} g_{r (k)} f_{k} + n_{2}) = \\ {v^{H}}_{k} g_{r (k)} a_{k} (\sqrt[]{P_{k}} h_{r (k)} w_{k} x_{k} + n_{1, k}) + {v^{H}}_{k} n_{2} = \\ \sqrt[]{P_{k}} a_{k} {v^{H}}_{k} g_{r (k)} h_{r (k)} w_{k} x_{k} + a_{k} {v^{H}}_{k} g_{r (k)} n_{1, k} + {v^{H}}_{k} n_{2} (4) \end{matrix} \end{matrix}$

式中: g_r₍ _k₎为第 k个中继节点至目的节点的信道增益; n₂为目的节点处的信道加性噪声矢量。

由式(4)可得相应的接收端信噪比(Signal to interference plus noise ratio, SINR)为:

$\begin{matrix} \begin{matrix} γ_{k} = \frac{a_{k}^{2} P_{k} {|{v^{H}}_{k} g_{r (k)} h_{r (k)} w_{k}|}^{2}}{a_{k}^{2} {|{v^{H}}_{k} g_{r (k)}|}^{2} σ_{n}^{2} + σ_{n}^{2}} = \\ \frac{ρ_{s} ρ_{r} {|{v^{H}}_{k} g_{r (k)} h_{r (k)} w_{k}|}^{2}}{ρ_{s} {|h_{r (k)} w_{k}|}^{2} + ρ_{r} {|{v^{H}}_{k} g_{r (k)}|}^{2} + 1} (5) \end{matrix} \end{matrix}$

式中: ρ_s =P_k/ $\begin{matrix} σ_{n}^{2} \end{matrix}$ ; ρ_r=P_r_, _k/ $\begin{matrix} σ_{n}^{2} \end{matrix}$ 。

通过采用迫零波束赋形技术和迫零检测接收技术,协作AF-MIMO系统得到了 L个相互之间无干扰的并行子信道。

综上所述,当选取 L个协作中继参与传输,同时采用迫零波束赋形技术和迫零检测接收技术,协作AF-MIMO系统的信道容量可以表示为:

$\begin{matrix} C_{sum} = \frac{1}{2} \overset{L}{\sum_{k = 1}} lo g_{2} (1 + γ_{k}) (6) \end{matrix}$

2 中继选择方案

2.1 系统条件

为了研究在给定协作AF-MIMO系统下的最佳中继选择问题,本节基于推导得出的协作AF-MIMO系统信道容量,对协作系统条件中的协作中继数目、协作中继位置和系统功率进行最优化分析,并依据各个条件与系统信道容量的关系得出协作系统条件的最优化结论。

2.1.1 协作中继数目

由式(6)可以看出,协作中继数目会对系统信道容量产生影响,所以首先研究协作中继数目的最优化问题,即确定在给定系统情况下的中继选择过程中需要选择的协作中继的具体数目。

由协作通信的相关知识可知,源节点和目的节点之间的空间虚拟子信道数目为min( M, N, L),当 L≤min( M, N)时,空间子信道数目随着协作中继数目的增加而增加,从而给协作AF-MIMO系统带来信道容量的大幅提升;当 L>min( M, N)时,系统空间子信道数目不会随着协作中继数目 L的增加而增加,为固定的min( M, N),因此过分地增加协作中继数目不能显著地增加协作AF-MIMO系统的信道容量。

另一方面,协作中继的继续增加会导致每个协作中继所分配的转发功率下降,影响最优中继VIR的性能,从而使系统信道容量可能出现不升反降的情况;同时大量加入的额外中继会带来一定的资源损耗(如硬件启动和关闭等过程的能量损耗),在一定程度上降低协作系统的总体性能。所以在给定的协作AF-MIMO系统下,选择的协作中继数目应满足:

$\begin{matrix} L = \min (M, N) (7) \end{matrix}$

当满足式(7)时,最佳中继选择过程随即停止,此时的系统总体性能达到最优。

综上所述:在源节点天线数目和目的节点天线数目相等的协作AF-MIMO系统中,选择的协作中继数目应与源节点天线数目和目的节点天线数目相等。在接下来的研究和分析中,系统的协作中继数目均满足 L=M=N。

2.1.2 系统功率

由式(5)和式(6)可知,在协作AF-MIMO系统中,系统的总发送功率和总转发功率也是影响信道容量的一个关键因素。在协作中继数目研究的基础上,对系统功率的最优化问题进行研究。

为了方便分析功率对信道容量的影响,设定接收天线处的噪声是均值为0、方差为 $\begin{matrix} σ_{n}^{2} \end{matrix}$ 的加性复高斯白噪声,源节点总发送功率为 P_s,中继节点总转发功率为 P_r,系统的源节点天线数目和目的节点天线数目相等,即 M=N,并且总发送功率和总转发功率均采用平均分配的方式,即 P_k=P_s /L、 P_r_, _k=P_r /L。协作中继数目为 L的情况下,源节点至中继节点即第一时隙的信道增益为 H_L= $\begin{matrix} [{h^{T}}_{r (1)}, \dots, {h^{T}}_{r (L)}]^{T} \end{matrix}$ ,( L×M),中继节点至目的节点即第二时隙的信道增益为 G_L=[ g_r₍₁₎,…, g_r₍ _L₎],( N×L)。由式(1)可以得出协作AF-MIMO系统第一时隙的信道容量为:

$\begin{matrix} C_{1} = \overset{L}{\sum_{k = 1}} lo g_{2} (1 + ρ_{s} {|h_{r (k)} w_{k}|}^{2}) (8) \end{matrix}$

由式(6)可以得出协作AF-MIMO系统第二时隙的信道容量为:

$\begin{matrix} \begin{matrix} C_{2} = \\ \overset{L}{\sum_{k = 1}} lo g_{2} (1 + \frac{ρ_{s} ρ_{r} {|{v^{H}}_{k} g_{r (k)} h_{r (k)} w_{k}|}^{2}}{ρ_{s} {|h_{r (k)} w_{k}|}^{2} + ρ_{r} {|{v^{H}}_{k} g_{r (k)}|}^{2} + 1}) (9) \end{matrix} \end{matrix}$

假设 P_s和 P_r均是变化的,但是系统总功率一定,即满足条件 P_r +P_s =2 P,以此来研究在给定条件下,改变 P_s或者 P_r对系统信道容量造成的影响。

由式(1)可以看出,协作AF-MIMO系统第一时隙的信道容量与 P_s呈正比例关系。下面研究在系统总功率一定,不断增加中继节点总转发功率的情况下,系统第二时隙信道容量的变化。

设定 P_r为自变量,同时有 P_s =2 P-P_r。对式(9)进行化简可得:

$\begin{matrix} C_{2} = \overset{L}{\sum_{k = 1}} lo g_{2} (1 + {|{v^{H}}_{k} g_{r (k)} h_{r (k)} w_{k}|}^{2} f (P_{r})) (10) \end{matrix}$

其中设关于自变量 P_r的函数为:

$\begin{matrix} f (P_{r}) = {(\frac{ρ_{s} {|h_{r (k)} w_{k}|}^{2} + ρ_{r} {|{v^{H}}_{k} g_{r (k)}|}^{2} + 1}{ρ_{s} ρ_{r}})}^{- 1} (11) \end{matrix}$

由于系统收发天线间的信道增益均是服从复高斯分布的随机变量,且均值为0,方差为 σ²,从统计平均的角度可以得出 $\begin{matrix} {|h_{r (k)} w_{k}|}^{2} \end{matrix}$ = $\begin{matrix} {|{v^{H}}_{k} g_{r (k)}|}^{2} \end{matrix}$ =b。将 $\begin{matrix} {|h_{r (k)} w_{k}|}^{2} \end{matrix}$ = $\begin{matrix} {|{v^{H}}_{k} g_{r (k)}|}^{2} \end{matrix}$ =b和 P_s +P_r =2 P代入到式(11)中进行化简处理,可得:

$\begin{matrix} \begin{matrix} f (P_{r}) = {(\frac{ρ_{s} {|h_{r (k)} w_{k}|}^{2} + ρ_{r} {|{v^{H}}_{k} g_{r (k)}|}^{2} + 1}{ρ_{s} ρ_{r}})}^{- 1} = \\ {(\frac{b (ρ_{s} + ρ_{r}) + 1}{ρ_{s} ρ_{r}})}^{- 1} = \\ \frac{1}{L σ_{n}^{2}} {(\frac{2 Pb + L σ_{n}^{2}}{P_{r} (2 P - P_{r})})}^{- 1} (12) \end{matrix} \end{matrix}$

式中:函数 f( P_r)的分母是关于自变量 P_r的二次函数。由数学知识可知,其二次函数曲线开口方向向下,并且随着 P_r的增加,曲线的变化趋势是先增大后减小,存在最大值点,即当满足 P_s =P_r =P时,函数 f( P_r)的分母取最大值,式(12)即取得最大值,同时根据式(9)和式(12)可以得出此时第二时隙的信道容量 C₂达到最大值。

2.2 中继选择算法

基于以上分析,提出了一种在AF-MIMO场景中天线功率未知情况下的中继选择算法(Relay selection with power unknown,RSPU)。该算法的实质是在系统无法准确获取节点功率信息的情况下,以所研究的系统条件为基础,利用仅有的信道CSI信息,通过循环迭代的方式,比较判别式得出最佳协作中继集合。

目标函数为:

$\begin{matrix} C = \frac{1}{2} \max \{\min [\begin{matrix} \overset{L}{\sum_{k = 1}} lo g_{2} (1 + ρ_{s} {|h_{r (k)} w_{k}|}^{2}), \\ \overset{L}{\sum_{k = 1}} lo g_{2} (1 + γ_{k}) \end{matrix}]\} (13) \end{matrix}$

把源节点 M看成一个整体,在第一次循环的时候遍历每个备选的中继节点,由式(13)推出判别式为:

$\begin{matrix} \begin{matrix} C_{r (k)} = \max \{\min [\begin{matrix} \det (h_{r (k)} \cdot {h^{H}}_{r (k)}), \\ \det (g_{r (k)} \cdot {g^{H}}_{r (k)}) \end{matrix}]\} \\ (14) \end{matrix} \end{matrix}$

由式(14)找到第一个最佳中继 r(1),同时得到信道 h_r₍₁₎和 g_r₍₁₎。在选定第一个最佳中继之后,进行第二次循环,去除掉最佳中继 r(1)并更新备选中继集合,然后将每个备选中继两端的信道与第一个最佳中继两端的信道进行合并,更新需要进行运算的信道矩阵为:

$\begin{matrix} \begin{matrix} h_{r (k)} = [{h^{T}}_{r (1)}, {h^{T}}_{r (k)}]^{T} (15) \\ g_{r (k)} = [g_{r (1)}, g_{r (k)}] (16) \end{matrix} \end{matrix}$

将式(15)和式(16)代入式(14)中继续求解,得到第二个最佳中继 r(2)。依次类推,最后得到 L个最佳协作中继,即得出最佳协作中继节点集合 r=[ r(1),…, r( L)]时结束循环。根据得到的最佳协作中继集合利用式(5)和式(6)计算出协作AF-MIMO系统的信道容量。

2.3 算法复杂度分析

RSPU算法在追求最大化信道容量的同时,也兼顾了算法复杂度。

多中继选择算法如下:

Input:H_s,r,G_r,d,k=1,…,K

Initialization:r=φ

for l=1,…,L

for k=1,…,K-{r}

更新信道矩阵h_r(k),g_r(k):

h_r(k)= $\begin{matrix} [h_{r (1)}^{T}, h_{r (k)}^{T}]^{T} \end{matrix}$

g_r(k)=[g_r(1),g_r(k)]

η_s,k=det $\begin{matrix} (h_{r (k)} \cdot h_{r (k)}^{H}) \end{matrix}$

η_k,d=det $\begin{matrix} (g_{r (k)} \cdot g_{r (k)}^{H}) \end{matrix}$

η_k=min $\begin{matrix} (η_{s, k}, η_{k, d}) \end{matrix}$

η= $\begin{matrix} [\begin{matrix} η & η_{k} \end{matrix}] \end{matrix}$

end

输出最佳协作中继的编号

[r(i),η_r(i)]=max(η)

更新最佳中继集合r和信道h_s,r,g_r,d

r=[r(1),…,r(i)]

h_s,r= $\begin{matrix} [h_{r (1)}^{T}, \dots, h_{r (i)}^{T}]^{T} \end{matrix}$

g_r,d=[g_r(1),…,g_r(i)]

end

Output:r,h_s,r,g_r,d

由算法可知,算法初始化的运算时间为2 K+4;算法的第 l次循环迭代的运算时间为4 +4 card( K) =4 +4( K+1 -l);在循环迭代结束后, r, h_s_, _r, g_r_, _d三个量在内循环的时候已经得出。假定算法终止时,循环共进行了 L次,则该算法的总运行时间为:

$\begin{matrix} \begin{matrix} T = (2 K + 4) + \overset{L}{\sum_{l = 1}} [4 + 4 (K + 1 - l)] = \\ (2 K + 4) + \overset{L}{\sum_{l = 1}} (4 K + 8 - 4 l) = \\ 4 KL - 2 L^{2} + 6 L + 2 K + 4 (17) \end{matrix} \end{matrix}$

且该算法至多能运行 K次,即 L≤ K,则有 T≤2 K² +8 L+4 =O( K²),所以RSPU算法的复杂度为 O( K²),对于给定 K的多中继系统而言,其运算复杂度是可以承受的。文献[5]中提到的GSO(Greedy semi-orthogonal relay selection)算法和MSR(Maximum sum rate relay selection)算法复杂度均为 O( K²),文献[6]中提到的剔除式中继选择算法的复杂度为 O( K³)。可见相对于已有算法,RSPU算法在运算复杂度方面没有提升。

3 仿真结果及分析

首先利用MATLAB对协作中继数目和信道容量的关系进行仿真验证。仿真条件:源节点和目的节点均设定4根天线,即 M=N=4;备选中继节点数目设置为80,每个节点配备一个天线,即 K=80;信道采用瑞利衰落信道,即信道增益为均值为0、方差为1的复高斯随机变量;源节点到目的节点没有直传链路;节点功率均采用平均分配的方式,并且有 P_s =P_r;噪声为均值为0、方差为1的加性高斯白噪声,采用RSPU算法进行中继选择。

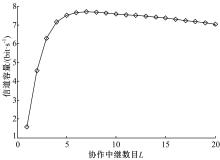
图3给出了当 M=N=4, L=20时随着协作中继数目的不断增加,系统信道容量的变化情况。由图可知,信道容量的变化趋势为先增加后减少,与理论分析得出的结论相符。同时相对于 L=3的情况,在 L=4时系统信道容量的提升幅度依然很大,而在 L=5时,系统信道容量提升幅度骤然变小。随着协作中继数目的进一步增加,甚至出现信道容量下降的情况。这是由于中继节点的总转发功率是一定的,不断的增加中继会使每个中继的转发功率下降,导致最优中继VIR的效率下降,致使系统信道容量出现降低的情况。

	Figure Option View Download New Window
	图3 M=N=4时系统信道容量Fig.3 Channel capacity for M=N=4

仿真结果表明,前面通过理论分析得出的结论是正确的,即在源节点数目与目的节点数目相同的AF-MIMO系统中,选取的协作中继数目等于源节点数是合理的。

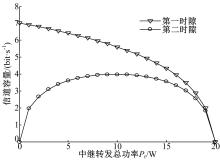
图4给出了协作系统在 M=N=L=4,且系统总功率满足 P_s+ P_r=20时,协作AF-MIMO系统双时隙信道容量随着中继节点总转发功率 P_r不断增加的变化情况。从图中可以看出,第一时隙的信道容量呈明显的下降趋势,曲线斜率由小到大,表明随着源节点总发送功率的不断减小,第一时隙信道容量的下降程度在不断增加。第二时隙的信道容量先是迅速提升,然后曲线斜率趋于零达到稳定的峰值点,此时第二时隙的信道容量达到最大;随着中继节点总转发功率的进一步增大,第二时隙信道容量趋于下降且下降速度在不断加快;同时第二时隙的信道容量曲线表现出了明显的对称性,在 P_r= P_s=10 W时系统信道容量达到最大,约为4.0 bit/s。

	Figure Option View Download New Window
	图4 双时隙信道容量Fig.4 Channel capacity for dual slot

仿真实验结果表明,在系统总功率一定的情况下,当源节点总发送功率与中继节点总转发功率相等,即 P_r= P_s时,第二时隙信道容量达到最大,即协作AF-MIMO系统信道容量达到最大。

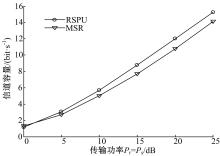
图5给出了在 M=N=4, K=80, P_s =P_r的条件下,本文提出的RSPU算法与文献[5]提出的MSR算法在不同传输功率情况下的系统信道容量的对比情况。可以看出,在发送功率较低的情况下,RSPU算法得到的信道容量的提升速率明显高于MSR算法;在传输功率大于15 dB的时候,两种算法得到的信道容量差值基本稳定,RSPU算法所得到的信道容量相比于MSR算法得到的信道容量提升了约1.0 bit/s。

	Figure Option View Download New Window
	图5 传输功率变化下的信道容量对比Fig.5 Comparison of the channel capacity achieved by changing the transmitted power

4 结束语

在AF-MIMO系统中,针对节点功率未知情况下的最佳协作中继选择问题,提出了一种基于信道CSI的中继选择算法,即RSPU算法。该算法以所研究的系统条件为基础,运用循环迭代的方式选择出最佳中继。该算法使用参数较少,在一定程度上简化了中继选择过程。仿真结果表明:在传输功率不同的条件下,通过RSPU算法选择出来的最佳中继使得系统的信道容量性能较已有算法有一定提升,验证了所提算法的有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Fan Y J, Thompson J. MIMO configurations for relay channels theory and practice[J]. IEEE Transactions on Wireless Communications, 2007, 6(5): 1774-1786. [本文引用:1] [JCR: 2.418]
[2]	Goldsmith A, Jafar S A, Jindal N, et al. Capacity limits of MIMO channels[J]. IEEE Journal on Selected Areas in Communication, 2003, 21(5): 684-702. [本文引用:1] [JCR: 3.121]
[3]	Lee K J, Hakjea S, Eunsung P, et al. Joint optimization for one and two-way MIMO AF multiple-relay systems[J]. IEEE Transactions on Wireless Communications, 2010, 9(12): 3671-3681. [本文引用:1] [JCR: 2.418]
[4]	Li Min, Lin Min, Yu Quan, et al. Optimal beamformer design for dual-hop MIMO AF relay networks over Rayleigh fading channels[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(8): 1402-1414. [本文引用:1] [JCR: 3.121]
[5]	Sun Liang, McKay M R. Opportunistic relaying for MIMO wireless communication: relay selection and capacity scaling laws[J]. IEEE Transactions on Wireless Communication, 2011, 10(6): 1786-1797. [本文引用:1] [JCR: 2.418]
[6]	Zeng Wei-liang, Xiao Cheng-shan, Wang You-zheng. Opportunistic cooperation for multi-antenna multi-relay networks[J]. IEEE Transactions on Wireless Communication, 2010, 9(10): 3189-3199. [本文引用:1] [JCR: 2.418]
[7]	Gharavi-Alkhansari M, Gershman A B. Fast antenna subset selection in MIMO systems[J]. IEEE Transactions on Signal Processing, 2004, 52(2): 339-347. [本文引用:1] [JCR: 2.813]
[8]	Amarasuriya G, Tellambura C, Ardakani M. Joint relay and antenna selection for dual-hop amplify-and -forward MIMO relay networks[J]. IEEE Transactions on Wireless Communication, 2012, 11(2): 493-499. [本文引用:1] [JCR: 2.418]
[9]	Chalise B, Zhang Y M, Amin M. Local CSI based selection beamforming for AF MIMO relay system with direct link[J]. IEEE Communications Letters, 2012, 16(5): 622-625. [本文引用:1] [JCR: 1.16]
[10]	Danaee A, Maleki M, Kota J S, et al. Relay and antenna selection in multi-antenna amplify-and -forward(AF) systems with partial channel state information[C]∥IEEE ICC 2012-Wireless Communication Symposium, Akron, 2012: 4155-4159. [本文引用:1]