收发频谱不一致条件下的变换域通信系统基函数设计

引用本文

谢铁城, 达新宇, 褚振勇, 张衡阳, 张磊. 收发频谱不一致条件下的变换域通信系统基函数设计. 44(6): 1825-1830
XIE Tie-cheng, DA Xin-yu, CHU Zhen-yong, ZHANG Heng-yang, ZHANG Lei. Basis function design for transform domain communication system in the presence of spectral mismatches. Journal of Jilin University Engineering and Technology Edition, 44(6): 1825-1830 复制到剪切板

Permissions

收发频谱不一致条件下的变换域通信系统基函数设计

谢铁城^1,², 达新宇¹, 褚振勇¹, 张衡阳¹, 张磊²

1.空军工程大学信息与导航学院,西安 710077

2. 94900部队,福建漳州 363000

作者简介:谢铁城(1983-),男,助理工程师,博士.研究方向:卫星变换域通信.E-mail:tie008@qq.com

基金:国家自然科学基金项目(60972042,61271250,61202490);

摘要

针对变换域通信系统收发频谱不一致条件下接收端基函数存在错误而导致系统性能下降的问题,提出了具有信噪比次优解的基函数设计方法。详细分析了系统的收发过程,在此基础上研究了系统误码率的最优化与接收端基函数组成的关系,在收发频谱不一致而无法获得最优基函数的情况下,采用类似等增益合并的方法设计了接收端基函数,从而以该基函数完成数据解调。仿真结果表明:在单用户和多用户环境下,当收发频谱不一致比例较高时,接收端采用类似等增益合并的基函数设计方法可以完成系统的次优接收。在单用户环境下,相比不一致比例为40%时,次优接收方法的信噪比增益可达4 dB左右,并且发送端频谱可用率为80%时,相比最优接收法的信噪比损失在1.5 dB以内。

关键词: 通信技术; 变换域通信系统; 基函数; 频谱不一致; 等增益合并; 信噪比次优解

中图分类号:TN914.42 文献标志码:A 文章编号:1671-5497(2014)06-1825-06

Basis function design for transform domain communication system in the presence of spectral mismatches

XIE Tie-cheng^1,², DA Xin-yu¹, CHU Zhen-yong¹, ZHANG Heng-yang¹, ZHANG Lei²

1.School of Information and Navigation, Air Force Engineering University, Xi'an 710077, China

2.Unit 94900 of PLA, Zhangzhou 363000, China

Abstract

The errors of the basis function in the receiver, caused by the difference of the spectrum environment between the transmitter and receiver of Transform Domain Communication System (TDCS), will degrade the system performance significantly. A design method of the basis function, which has suboptimal solution of the Signal-to-Noise Ratio (SNR), is proposed to solve this problem. Based on a detailed study of the data sending and receiving process, the optimized Bitter Error Rate (BER) of the system and its relationship with the basis function of the receiver is discussed. In the case that the system with spectral mismatches can not obtain the optimal basis function, a design method of the basis function similar to equal-gain combing is proposed, and then this basis function is used for modulation. Simulation results show that, in the conditions of both multi-user and single-user with high spectral mismatch ratio, the receiver is suboptimal when the basis function is designed similar to equal-gain combing. In the single-user condition, the BER performance improvement of suboptimal reception is approximately 4 dB compared with the reception method when the mismatch ratio is 40%, and the SNR loss is below 1.5 dB at the spectral efficiency of 80% compared with the optimal reception.

Keyword: communication; transform domain communication system; basis function; spectral mismatches; equal gain combing; signal-to-noise ratio suboptimal solution

Show Figures

0 引言

变换域通信系统(Transform domain communication system,TDCS)是一种在认知无线电(Cognitive radio,CR)、扩频通信和变换域处理技术基础上发展起来的无线通信系统,它具有良好的抗干扰和抗截获能力以及容易实现多址通信等优点^{[ 1, 2]}。基函数的设计是实现系统性能的关键,同时,基函数的错误也极大地限制了系统的抗干扰性能^{[ 3, 4, 5]}。基函数频域形式是由幅度谱向量与等长度的复伪随机相位向量做数量积得到,其中幅度谱向量由收发两端在给定系统带宽内感知频谱使用情况并标记后而得到,复伪随机相位向量则由相位映射器产生。收发两端频谱环境的不一致必然导致估计的幅度谱向量不相同,由此造成接收端的基函数相对于发送端产生错误,从而影响了系统的通信效果^{[ 6, 7]}。因此,收发频谱不一致的通信问题一直得到人们的广泛关注。

尽管如此,近年来国内外关于TDCS的研究大多以收发频谱一致为前提条件^{[ 8, 9, 10, 11]},而关于基函数不同的研究较少。其中,文献[3]通过仿真验证了频谱不一致会导致系统误码率性能急剧下降,并发现接收机频谱估计错误给系统造成的影响要大于发射端频谱估计错误带来的影响,但如何解决这一问题文中并未给出。文献[4-5]在认知无线通信网络场景中通过建立公共控制信道实现双方频谱检测结果的传输和交换。文献[12]在此基础上申请了这种链路建立方法的专利。显然,建立公共控制信道的方法会增加系统复杂度,并且不适用于其他应用领域,如军用通信领域,增加公共控制信道还需要考虑其自身的通信保密问题,因此,这种方法并不是最理想的解决方案。

针对这种现状,本文提出了一种收发频谱不一致条件下的基函数设计方法,通过详细分析系统的收发过程,推导了误码率的解析表达式,以此为基础研究了收发两端基函数与接收信号信噪比的内在关系,在由于接收端与发送端频谱不一致而无法获得准确基函数的情况下,设计了具有信噪比次优解的接收端基函数幅度谱,从而完成相关解调,实现信号接收。该方法能改善收发频谱不一致条件下的系统误码性能,且复杂度低,能适用于各种应用领域。

1 系统信号模型

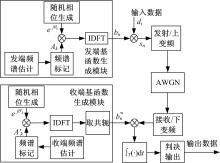
图1为TDCS收发端通用模型,图中分别标出了各个节点信号的表示符号,为了便于分析,取信道为加性高斯白噪声信道,且暂不考虑信号发射和接收的上下变频过程。

收发两端均在给定系统带宽内感知频谱的使用情况,并标记空闲频谱,将感知得到的频谱向量与选定的门限值比较,高于门值的谱值设为0;低于门限值的谱值则设为1,由此生成基函数幅度谱向量,再与复伪随机相位向量做数量积得到频域基函数,最后进行傅立叶反变换得到时域基函数。

	Figure Option View Download New Window
	图1 变换域通信系统收发端模型Fig.1 The transceiver model of TDCS

假设系统中共有 U个完全相同的、独立的并且同步的用户,第 v个用户发送端基函数 b_v的离散序列可表示为:

$\begin{matrix} \begin{matrix} b_{v, n} = \frac{1}{\sqrt[]{N}} \overset{N - 1}{\sum_{k = 0}} c_{v} A_{v, k} e^{j θ_{v, k}} e^{\frac{j 2 π kn}{N}} (1) \\ n = 0,1, \dots, N - 1 \end{matrix} \end{matrix}$

式中: $\begin{matrix} e^{j θ_{v, k}} \end{matrix}$ 为复伪随机相位, θ_v_, _k服从[0,2π]均匀随机分布; c_v为功率调整因子,且 c_v= $\begin{matrix} \sqrt[]{N / N_{v, A}} \end{matrix}$ , N_v_, _A为第 v用户基函数频谱幅值为1的个数。

发送端以此基函数对信息数据进行调制并发射至信道传输,常见的调制方式有MCSK与MPSK。经过调制后信号可表示为:

$\begin{matrix} \begin{matrix} s_{v, n} = \frac{1}{\sqrt[]{N}} \overset{N - 1}{\sum_{k = 0}} c_{v} A_{v, k} e^{j θ_{v, k}} e^{j θ_{v, s}} e^{\frac{j 2 πkn}{N}} (2) \\ n = 0,1, \dots, N - 1 \end{matrix} \end{matrix}$

当调制方式为MCSK时, $\begin{matrix} e^{j θ_{v, s}} \end{matrix}$ = $\begin{matrix} e^{- j 2 π d_{v, i} k / M} \end{matrix}$ ;而调制方式为MPSK时, $\begin{matrix} e^{j θ_{v, s}} \end{matrix}$ = $\begin{matrix} e^{j 2 π d_{v, i} / M} \end{matrix}$ ,其中 M为调制阶数, d_v_, _i为用户 v第 i次发送的信息数据,0≤ d_v_, _i≤ M-1,且为均匀分布。

用户 v接收端使用本地基函数的共轭对接收信号进行相关解调,接收信号由用户 v调制信号、其他用户调制信号干扰和噪声三部分组成。经过下变频,接收信号为:

$\begin{matrix} r_{v} = s_{v} + \overset{U - 1}{\sum_{u = 0, u \neq v}} j_{u} + z_{v} (3) \end{matrix}$

式中: s_v为用户 v已调制信号; j_u为第 u个用户已调制信号; z_v为均值为0,方差为 N₀ /2的高斯随机向量。

经过相关接收,用户 v接收到的第 i个数据的解调信号为:

$\begin{matrix} y = r_{i, v} \cdot b_{v}^{'H} = \overset{N - 1}{\sum_{n = 0}} (s_{v, n} + \overset{U - 1}{\sum_{u = 0, u \neq v}} j_{u, n} + z_{v, n}) b_{v, n}^{'*} (4) \end{matrix}$

式中:(·)^H表示共轭转置:

$\begin{matrix} \begin{matrix} j_{u, n} = \frac{1}{\sqrt[]{N}} \overset{N - 1}{\sum_{k = 0}} c_{u} A_{u, k} e^{j θ_{u, k}} e^{j θ_{u, s}} e^{\frac{j 2 πkn}{N}} (5) \\ b_{v, n}^{'*} = \frac{1}{\sqrt[]{N}} \overset{N - 1}{\sum_{k = 0}} c'_{v} A'_{v, k} e^{- jθ'_{v, k}} e^{- \frac{j 2 πkn}{N}} (6) \end{matrix} \end{matrix}$

式中: A_u_, _k、 θ_u_, _k和 θ_u_, _s分别为用户 u发送端基函数幅度谱、伪随机相位和发送信息数据的调制相位; c'_v、 A'_v_, _k和 θ'_v_, _k分别为用户 v接收端功率调整因子、基函数幅度谱和伪随机相位,并且当收发频谱一致时 c'_v=c_v、 A'_v_, _k=A_v_, _k和 θ'_v_, _k=θ_v_, _k。

2 频谱不一致条件下的基函数设计

2.1 收发频谱不一致对系统接收性能的影响

TDCS收发基函数不一致将极大影响系统的误码性能。下面以MPSK调制的信号接收为例,分析收发频谱不一致对系统接收性能的影响。

将式(5)(6)代入式(4),并化简可得:

$\begin{matrix} \begin{matrix} y = c_{v} c'_{v} \overset{N - 1}{\sum_{k = 0}} A_{v, k} A'_{v, k} e^{j (θ_{v, k} - θ'_{v, k})} e^{j θ_{v, s}} + \\ \overset{U - 1}{\sum_{u = 0, u \neq v}} c_{u} c'_{v} \overset{N - 1}{\sum_{k = 0}} A_{u, k} A'_{v, k} e^{j (θ_{u, k} - θ'_{v, k})} e^{j θ_{u, s}} + \\ c'_{v} \overset{N - 1}{\sum_{k = 0}} Z_{k} A'_{v, k} e^{- jθ'_{v, k}} (7) \end{matrix} \end{matrix}$

式中:等式右边第1项为有用相关信号分量 y_s;第2项为其他用户信号干扰分量 y_j,如果各用户伪随机相位序列正交性好则本项可忽略不计;第3项为噪声分量 y_z; Z_k为噪声频谱幅值。

当调制方式为MPSK且收发频谱相同时,经过相关接收,用户 v接收到的第 i个数据的解调信号为:

$\begin{matrix} y = c_{v}^{2} \overset{N - 1}{\sum_{k = 0}} A_{v, k}^{2} e^{j 2 π d_{v, i} / M} + y_{z} (8) \end{matrix}$

此时根据解调信号矢量所处的扇区位置便可判断所解调的数据。当收发频谱不一致时,对比式(7)与式(8)可以看出:尽管有用相关信号矢量相位不变,但是幅值发生了变化,有用相关信号与噪声分量的矢量和,即解调信号矢量也因此产生了变化,从而影响了最终的判决结果。

2.2 基函数组成与系统性能的关系

当系统采用MPSK调制,TDCS系统误码率为 P_e≈ Q( $\begin{matrix} \sqrt[]{2 SINR} \end{matrix}$ sin $\begin{matrix} \frac{π}{M} \end{matrix}$ ),若采用MCSK调制,则TDCS系统误码率为 P_e≤( M-1) Q( $\begin{matrix} \sqrt[]{SINR} \end{matrix}$ ),其中 Q( x) = $\begin{matrix} \frac{1}{\sqrt[]{2 π}} \end{matrix} \begin{matrix} \int_{x}^{\infty} \end{matrix} \begin{matrix} e^{- z^{2} / 2} \end{matrix}$ d z, SINR为信号干扰噪声比:

$\begin{matrix} SINR = \frac{{E {[y]}}^{2}}{Var (y)} = \frac{| y_{s} |^{2}}{| y_{j} |^{2} + | y_{z} |^{2}} (9) \end{matrix}$

可以看出,不管采用哪种调制方式,在调制阶数确定的情况下,系统误码性能均由信号干扰噪声比决定。

进一步由式(9)可得:

$\begin{matrix} SINR = \frac{| y_{s} |^{2}}{| y_{j} |^{2} + | y_{z} |^{2}} \leq \frac{| y_{s} |^{2}}{| y_{z} |^{2}} (10) \end{matrix}$

这是考虑到当其他用户干扰信号存在时,在满足理想条件下,即不同用户的基函数的伪随机相位之间满足正交性,接收端基函数幅度谱值的变化对其他用户干扰信号的功率影响可以忽略不计。因此以式(10)的不等号右边一项为条件,分析接收端基函数组成与系统性能的关系是合理且可行的。

利用Schwartz不等式,有:

$\begin{matrix} | \overset{N - 1}{\sum_{k = 0}} α_{k} β_{k}^{*} |^{2} \leq (\overset{N - 1}{\sum_{k = 0}} | α_{k} |^{2}) (\overset{N - 1}{\sum_{k = 0}} | β_{k} |^{2}) (11) \end{matrix}$

式(11)等号成立的条件为 α_k=ηβ_k, k=0,1,…, N-1且 η为常数。现令:

$\begin{matrix} α_{k} = A_{v, k} e^{j θ_{v, k}}, β_{k} = A'_{v, k} e^{jθ'_{v, k}} (12) \end{matrix}$

将其代入式(11)可得:

$\begin{matrix} \begin{matrix} | \overset{N - 1}{\sum_{k = 0}} A_{v, k} A'_{v, k} e^{j (θ_{v, k} - θ'_{v, k})} |^{2} \leq \\ (\overset{N - 1}{\sum_{k = 0}} | A_{v, k} |^{2}) (\overset{N - 1}{\sum_{k = 0}} | A'_{v, k} |^{2}) (13) \end{matrix} \end{matrix}$

于是由式(10)与式(13)可得:

$\begin{matrix} SINR \leq c_{v}^{2} (\overset{N - 1}{\sum_{k = 0}} | A_{v, k} |^{2}) \frac{2}{N_{0}} (14) \end{matrix}$

其中取 |y_z|² =( $\begin{matrix} \overset{N - 1}{\sum_{k = 0}} \end{matrix}$ |A'_v_, _k $\begin{matrix} e^{jθ'_{v, k}} \end{matrix}$ |²) $\begin{matrix} \frac{N_{0}}{2} \end{matrix}$ 。当且仅当 A_v_, _k $\begin{matrix} e^{j θ_{v, k}} \end{matrix}$ =A'_v_, _k $\begin{matrix} e^{jθ'_{v, k}} \end{matrix}$ 时,不等式(14)的等号成立。

综合以上分析可以得出,由于 Q函数是关于变量的单调递减函数,对于接收端相关接收来说,当收发频谱相同,即满足不等式(14)的等号成立的条件下,接收信号干扰噪声比取值最大,此时系统误码性能最好。当收发频谱不一致时,当接收端以估计己方频谱得到的基函数去完成相关解调时,如果发送端基函数幅度谱值 A_v_, _k=1,而基函数幅度谱值 A'_v_, _k错误地估计为0,从能量角度上讲,相当于使接收的有用信号能量下降,从而影响了系统的误码性能。

2.3 基于分集接收思想的接收端基函数设计

进一步分析式(10)和式(13)还可以发现:对于TDCS相关接收,接收端有用信号能量相当于收发两端基函数序列相对应幅度谱值与相位之积的线性组合的平方,这与多径衰落信道上的分集合并接收原理是类似的。因此,在收发端频谱是否一致未知的情况下,可以借鉴分集接收的思想,利用已有成熟的分集接收技术应用于接收端基函数的设计。

在分集技术中合并方式有选择合并、最大比合并、等增益合并以及平方律合并等。其中平方律合并属于非相干合并方式,与TDCS的相关接收原理不相符,因此不能适用于基函数设计。而选择合并和最大比合并均需要幅度衰减和相移的先验信息,收发频谱不一致时只能提供相位的先验信息,因此这两种方法也不能适用于基函数设计。

在分集合并中等增益合并的性能仅次于最大比合并,并且它只对各支路的相位进行校正,而各支路的增益加权是相等的,显然,这对于收发频谱不一致时的基函数设计是可行且容易的,基函数相位已事先获得,而基函数幅度谱值可取值为1,并作归一化即可。此时,解调信号可化简为:

$\begin{matrix} \begin{matrix} y = c_{v}^{2} \overset{N - 1}{\sum_{k = 0}} A_{v, k} e^{j θ_{v, s}} + \overset{U - 1}{\sum_{u = 0, u \neq v}} c_{u} c_{v} \overset{N - 1}{\sum_{k = 0}} A_{u, k} \cdot \\ e^{j (θ_{u, k} - θ_{v, k})} e^{j θ_{u, s}} + c_{v} \overset{N - 1}{\sum_{k = 0}} Z_{k} e^{- j θ_{v, k}} (15) \end{matrix} \end{matrix}$

根据式(9)即可求得信号干扰噪声比和系统误码率。

除此之外,当收发频谱不一致时,基函数的设计还可以采取随机赋值的方式,即对接收端基函数幅度谱随机赋值并作归一化,此时收发基函数幅度谱序列值存在不同的错误个数,这与接收端估计本地与发送端不一致程度是类似的。

当采用随机赋值的设计时,接收信号干扰噪声比与幅度谱的错误个数有密切的关系,错误的个数越多,系统性能越差,因此这种设计方法很难得到系统的误码性能表达式。而类似等增益合并的设计方法与收发频谱的不一致程度无关,从式(15)也可以看出,其系统误码性能仅与发送端频谱的可用比例(即幅度谱值为1的比例)有关。

在发送端频谱可用比例相同的条件下,采用随机赋值设计的系统性能还与收发幅度谱不一致的个数有关,因此,当对于收发频谱一致条件下的正常接收即最优接收,等增益合并的设计方法属于一种次优的设计方法。

3 仿真验证

仿真条件:设基函数幅度谱周期长度为64(便于做傅氏变换),复伪随机相位按[0,2π]均匀分布随机产生。基函数采用共轭对称频谱,即频谱幅值成偶对称,相位成奇对称。发送端基函数频谱可用比例分别取40%、50%、60%、70%和80%。收发频谱不一致的比例取0、40%和80%。系统采用BPSK调制,发送数据按独立同分布等概率产生,信道为高斯白噪声信道,并假设系统具有理想的同步。仿真中的每个点均取5000次仿真的平均值。

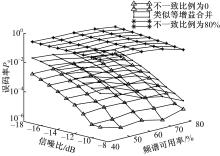
图2为单用户条件下采用类似等增益合并和随机赋值的基函数设计的系统误码率曲线图,其中不一致比例为0时,指的是收发频谱一致时接收端获得正确的发送端基函数而实现的最优接收方法。可以明显看出,在最优接收条件下系统误码性能要好于其他情况。当不一致比例达80%时,系统误码性几乎无法满足系统要求。相比之下,在收发频谱不一致条件下采用次优的接收方法则在一定程度上能够改善系统的误码性能,并且随着频谱可用率的提高,系统的误码性能还能进一步提高,这也与其物理概念是相吻合的,即发送端基函数的频谱可利用率越高,与接收端采用类似等增益合并的基函数则越相近,因此,接收误码率也越低。

	Figure Option View Download New Window
	图2 不同基函数设计的接收误码特性(单用户)Fig.2 BER performance of different basis functions design(single-user)

	Figure Option View Download New Window
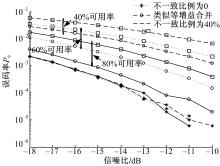	图3 不同频谱可用率条件下的误码特性比较(单用户)Fig.3 BER performance comparison among different spectral efficiency(single-user)

图3给出了单用户条件下发送端基函数频谱可用率取40%、60%和80%时不同基函数设计的系统误码率比较图,其中随机赋值方法的基函数不一致比例分别取0和40%。可以看出,当不一致比例为0时,发送端的频谱可用率对系统误码性能影响不大,而另外两种方法随着频谱可用率的提高,系统误码性能也随之提高。在同一误码率和频谱可用率条件下,类似等增益合并的方法相比较于不一致比例为40%时均能带来4 dB左右的信噪比增益。而频谱可用率为80%时,类似等增益合并方法比不一致比例为0时的信噪比损失均在1.5 dB以内。

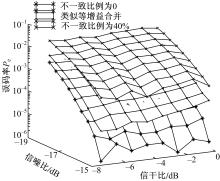
图4为系统中存在另外一个TDCS用户条件下3种基函数设计的系统误码率曲线图,其中己方发送端基函数频谱可用率设为80%,并且与他方TDCS基函数有较好的正交性。收发频谱不一致比例取为40%,仿真中取己方信号与他方信号的功率比,即信干比为-8~0 dB。从图4中可以看出:在有其他用户存在的条件下,接收端类似等增益合并的接收方法依然能够改善直接估计接收的方法,从而也验证了在多用户存在的条件下,类似等增益合并的基函数设计同样是一种具有误码率次优解的方法。

图5给出了与图3相同设计条件下,信干比取0、-2、-4 dB时几种基函数设计的系统误码率比较图。

	Figure Option View Download New Window
	图4 不同基函数设计的接收误码特性(2个用户)Fig.4 BER performance of different basis functions design(two users)

	Figure Option View Download New Window
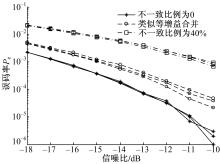	图5 不同信干比条件下的误码特性比较(2个用户)Fig.5 BER performance comparison among different signal-interference ratio (two users)

从图5中可以看出,当系统中用户基函数正交条件下,3种基函数设计方法的接收误码率受信干比变化的影响较小,在较高的己方发送端基函数可用率条件下,类似等增益方法的误码率接近于不一致比例为0时的误码率,却远低于不一致比例为40%时的误码率,这与单用户条件下的接收性能曲线是一致的。

4 结束语

在详细分析TDCS系统误码率与收发基函数关系的基础上,设计了一种类似等增益合并的具有次优误码性能的接收端基函数幅度谱,并以此完成接收信号解调,解决了TDCS收发两端频谱环境不一致条件下接收端获得的本地基函数与发送端存在错误而导致系统接收性能急剧下降的问题。理论分析与仿真试验均验证了该方法的可行性和有效性。这对于提高TDCS收发端距离较远时频谱不一致条件下的系统信号接收能力,拓展TDCS的应用领域具有一定的理论意义和实用价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chakravarthy V, Shaw A K, Temple M A, et al. Cognitive radio-an adaptive waveform with spectral sharing capability[C]∥IEEE Proc IEEE Wireless Communications and Networking Conference, Piscataway N J, USA, 2005: 724-729. [本文引用:1]
[2]	Chakravarthy V, Nunez A S, Stephens J P, et al. TDCS, OFDM, MC-CDMA: a brief tutorial[J]. IEEE Radio Communications, 2005, 43(9): S11-S16. [本文引用:1]
[3]	Liu J Y, Su Y T. Performance analysis of transform domain communication systems in the presence of spectral mismatches[C]∥IEEE Proc IEEE MILCOM 2007, Orland o F L, USA, 2007: 1-5. [本文引用:1]
[4]	Ni Shui-ping, Deng Li-heng. Application on OFDM-based transform domain communication system in mine[C]∥Proc International Conference on Electrical Information and Mechatronics, Germany, 2012: 843-848. [本文引用:1]
[5]	Fumat G, Chargé P, Zoubir A, et al. Enhancing spectral efficiency of Transform Domain Communication Systems by using a multidimensional modulation[C]∥IEEE Proc 6th International ICST Conference on Cognitive Radio Oriented Wireless Networks and Communications, Piscataway N J, USA, 2011: 131-135. [本文引用:1]
[6]	陈韵, 王逸林, 蔡平, 等. 基于分数阶Fourier 变换的远程水声通信技术研究[J]. 兵工学报, 2011, 32(9): 1159-1164. Chen Yun, Wang Yi-lin, Cai Ping, et al. Research on long range underwater acoustic communication technology based on fractional fourier transform[J]. Acta Armamentarii, 2011, 32(9): 1159-1164. [本文引用:1] [CJCR: 0.5149]
[7]	谢铁城, 达新宇, 褚振勇, 等. 采用时频分析的变换域通信系统基函数设计[J]. 西安交通大学学报, 2012, 46(6): 42-47. Xie Tie-cheng, Da Xin-yu, Chu Zhen-yong, et al. Design of basis functions for transform domain communication systems using time-frequency analysis[J]. Journal of Xi'an Jiaotong University, 2012, 46(6): 42-47. [本文引用:1] [CJCR: 0.0348]
[8]	Fumat G, Chargé P, Zoubir A, et al. Using set theoretic estimation to address the PAPR problem of spectrum-constrained signals[J]. IEEE Transactions on Wireless Communications, 2012, 11(7): 2373-2381. [本文引用:1] [JCR: 2.418]
[9]	Su Hu, Guan Yong-liang, Bi Guo-an, et al. Cluster-based transform domain communication systems for high spectrum efficiency[J]. IET Communications, 2012, 16(6): 2734-2739. [本文引用:1] [JCR: 0.637]
[10]	Lu Wei-dang, Gong Yi, Ting S H, et al. Cooperative OFDM relaying for opportunistic spectrum sharing: protocol design and resource allocation[J]. IEEE Transactions on Wireless Communications, 2012, 11(6): 2126-2135. [本文引用:1] [JCR: 2.418]
[11]	孙海欣, 石要武, 于晓辉. 基于扩频相位编码的变换域通信系统多址接入能力[J]. 吉林大学学报: 工学版, 2013, 43(1): 223-228. Sun Hai-xin, Shi Yao-wu, Yu Xiao-hui. Multiple access capability for spread coding based transform domain communication system[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(1): 223-228. [本文引用:1] [CJCR: 0.701]
[12]	韩川, 王军, 李少谦. 一种认知无线电场景中的链路建立方法[P]. 中国: 200610020703. 6, 2009-03-18. [本文引用:1]

2005

0.0

2005

0.0

2007

0.0

2012

0.0

2011

0.0

2011

0.0

0.5149

. 2011, 32(9):1159-1164

Research on long range underwater acoustic communication technology based on fractional fourier transform

(Science and Technology on Underwater Acoustic Laboratory, Harbin Engineering University, Harbin 150001，Heilongjiang, China)

Aimed at short propagation distance and poor anti-jamming capability of narrow-band signal in underwater acoustic (UWA) communication, a new UWA communication scheme is proposed on the basis of fractional Fourier transform which used LFM signals as carrier signals. LFM signals are divided into groups as coding signals in time domain and the coding signals are decoded by using pulse position modulation (PPM) in fractional domain. A Rake receiver is presented to suppress UWA channel’s multi-path effect which could lead to inter-symbol interference (ISI). Comparing to traditional UWA communication, this scheme has strong anti-interference ability and high communication rate; the maximum communication rate can be up to 800 bit/s. The feasibility and robustness of this system are verified through simulations, and it is helpful to the long range UWA communication.

针对水声通信中所采用的窄带信号传输距离近和抗干扰能力不足的问题，提出一种采用线性调频(LFM)作为载波信号，采用分数阶Fourier变换作为解码方式的水声通信方案。该方案采用在时域进行LFM信号的码元分割，在分数阶变换域借用脉冲位置调制(PPM)进行解码的方法进行通信，并通过Rake接收机进行路径分集接收抑制水声信道多途效应所产生的码间干扰(ISI). 该通信方案发挥了分数阶Fourier变换抗干扰能力强的优点，并且相较于传统水声通信方法具有通信速率高的特点，最高通信速率可达800 bit/s. 通过大量仿真验证了该方案的可行性和鲁棒性，可应用于远程水声通信。

2012

0.0

0.0348

2012

2.418

0.0

2012

0.637

0.0

2012

2.418

0.0

2013

0.0

0.701

. 2013, 43(1):223-228

Multiple access capability for spread coding based transform domain communication system

1. School of Electronic and Information Engineering, Changchun University, Changchun 130022, China;<br />2. College of Communication Engineering, Jilin University, Changchun 130022, China

The random phase coding method of Transform Domain Communication System (TDCS) is studied. To improve the multiple access capability, a new Spread Phase Coding TDCS (SPC-TDCS) scheme is proposed. The framework of the SPC-TDCS is given. The selection of the spread sequence and the cross correlation of the spread basic function are studied, the system performances of the proposed SPC-TDCS are analyzed. Simulation results demonstrate that the proposed scheme has good system performance in a multiple access environment and guarantees the minimum interference among different users at the same time.

为了改善变换域通信系统(Transform domain communication system,TDCS)的多址接入能力,提出基于扩频相位编码(Spread phase coding,SPC)的TDCS方案SPC-TDCS,给出了其系统框架,对扩频序列的选取及扩频基函数的互相关性进行了研究,并对SPC-TDCS的系统性能进行了分析。仿真结果表明,提出的SPC-TDCS具有良好的多址接入能力,同时保证用户间干扰最小。

0.0