基于搜索范围预测的直扩系统多普勒频偏估计

引用本文

胡梅霞, 刘毅, 卢满宏, 张兆维, 李勇朝. 基于搜索范围预测的直扩系统多普勒频偏估计. 44(6): 1838-1842
HU Mei-xia, LIU Yi, LU Man-hong, ZHANG Zhao-wei, LI Yong-zhao. Searching range prediction based on Doppler frequency shift estimation method in direct spread spectrum systems. Journal of Jilin University Engineering and Technology Edition, 44(6): 1838-1842 复制到剪切板

Permissions

基于搜索范围预测的直扩系统多普勒频偏估计

胡梅霞¹, 刘毅¹, 卢满宏², 张兆维¹, 李勇朝¹

1.西安电子科技大学综合业务网理论及关键技术国家重点实验室,西安 710071

2.北京遥测技术研究所,北京 100076

通信作者:李勇朝(1974-),男,教授,博士生导师.研究方向:宽带无线通信,通信信号处理,空间信息网络.

作者简介:胡梅霞(1978-),女,博士研究生.研究方向:无线通信.E-mail:mxhu@mail.xidian.edu.cn

基金:高等学校学科创新引智计划项目(B08038); 国家自然科学基金项目(61301169,61201134,61371127); 新世纪优秀人才支持计划项目(NCET-12-0918,72131855); 高等学校博士学科点专项科研基金资助课题(20120203110002); 国家重大科技专项(20132X03003008-004); 综合业务网理论及关键技术国家重点实验室项目(ISN090105); 中央高校基本科研业务费专项基金项目(7214466701);

摘要

为了解决极低信噪比和高动态条件下多普勒频偏估计可靠性差的问题,提出了一种基于搜索范围预测的扩频系统多普勒频偏估计方法。该方法利用相邻接收信号之间多普勒频偏变化受限的特点,用已得到的多普勒频偏估计值来缩小后续频偏估计的搜索范围,从而提高多普勒频偏估计的可靠性。仿真结果表明:该方法可以有效地提升多普勒频偏估计的可靠性。

关键词: 信息处理技术; 极低信噪比; 高动态; 多普勒估计; 搜索预测

中图分类号:TN914.42 文献标志码:A 文章编号:1671-5497(2014)06-1838-05

Searching range prediction based on Doppler frequency shift estimation method in direct spread spectrum systems

HU Mei-xia¹, LIU Yi¹, LU Man-hong², ZHANG Zhao-wei¹, LI Yong-zhao¹

1.State Key Laboratory of Integrated Services Networks, Xidian University, Xi'an 710071, China

2.Telemetry Technology Institute, Beijing 100076, China

Abstract

To improve the unreliable Doppler frequency estimation under the condition of extremely low SNR and high dynamic state, a searching range prediction method was proposed based on Doppler frequency shift estimation used in spread spectrum systems. Using Doppler frequency variation limitation over adjacent two received signals, the proposed method narrows the searching range of the later estimations from the previous estimation results, thus, enhancing the estimation reliability. Simulation results show that this proposed method can effectively increase the Doppler detection reliability.

Keyword: information processing; extremely low SNR; high dynamic; Doppler estimation; searching prediction

Show Figures

0 引言

在飞行器测控通信系统中,为了克服由高移动性引起的大多普勒对通信质量的影响,接收端必须实施快速、准确的多普勒频偏捕获,将剩余多普勒频偏缩小到跟踪环路入锁频偏动态范围之内,以便进行多普勒跟踪过程。

现有的大多普勒频移估计算法主要有基于FFT的功率谱检测算法^{[ 1, 2, 3]}、基于噪声匹配的算法^{[ 4]}、采用三阶段机制进行合码捕获和多普勒频偏估计的算法^{[ 5]}以及采用半分法进行迭代搜索的多普勒频偏估计算法^{[ 6]}等。但是上述几种算法都仅考虑了恒定的多普勒频偏,没有考虑多普勒加速度对频偏估计的影响。

当接收信噪比不足以保证一个可靠的多普勒频偏估计时,可通过相干或非相干累加^{[ 7]}来累积信号能量,从而有效提升接收端信噪比。但是,当多普勒频偏具有较大的动态加速度时,频域信号位置会随时间的累加而发生漂移^{[ 8]},并且最佳累加时间随加速度的增加而减小,这给多普勒频偏的准确估计带来较大难度。文献[9]在一定累加周期上通过相关积分来抑制多普勒加速度变化对多普勒频偏估计的影响,但是这仍然不能改善接收信号最佳累积时间过短的问题。在DSSS系统中,文献[10]采用分段运动补偿技术来抑制高动态多普勒抖动问题,从而提高接收机的捕获灵敏度。文献[11]在一定累加周期上,首先对多普勒加速度进行估计,然后在对多普勒加速度进行补偿之后再进行多普勒频偏估计。类似于文献[11],文献[12]提出了一种基于插值的频偏和频率斜升联合估计算法,以频率斜升粗估计结果为中心,对频率斜升进行二次插值得到频率斜升值,然后计算该估计值下的频偏估计值。但是以上这几种需要估计频率加速度的方法仅仅适用于加速度恒定的运动情形。

针对极低信噪比和高动态对多普勒频偏估计的双重影响,本文给出了一种适用于极低信噪比高动态环境下的基于搜索范围预测的多普勒频偏估计方法。该方法在基于FFT功率检测的多普勒频偏估计算法基础上,充分利用前后信号之间多普勒频偏变化受限这一物理特点,通过迭代不断缩小频率检测的有效搜索范围,提高频偏估计的可靠性。

1 系统模型

假定系统接收端经载波解调、中频DDC和滤波抽取之后,得到的基带扩频信号为 r_n:

$\begin{matrix} r_{n} = b_{n} \cdot c_{n} \cdot \exp (j 2 π (f_{d 0} + \frac{a}{2} n) n + j φ_{c}) + ω_{n} (1) \end{matrix}$

式中: b_n∈{ +1, -1}为极性未知的信息码元序列; c_n∈{ +1, -1}为扩频码序列; ω_n是均值为0、均方差为 σ²的加性复高斯白噪声; f_d0为多普勒频偏初值; a为多普勒频偏一次加速度; φ_c为载波固有相位差。

2 基于FFT功率检测的多普勒频偏估计算法

当码元理想同步时,在接收端用已知的扩频码对接收信号进行解扩得到

$\begin{matrix} {\bar{r}}_{n} = b_{n} \cdot \exp (j 2 π (f_{d 0} n + \frac{a}{2} n^{2}) + j φ_{c}) + ω_{n} \cdot c_{n} (2) \end{matrix}$

在每个码元持续时间内,当多普勒一次加速度 a对多普勒频偏的影响可以忽略不计时, $\begin{matrix} {\bar{r}}_{n} \end{matrix}$ 近似为一个单频信号。这样,当接收信噪比较高时,可以对一个扩频码周期长的信号 $\begin{matrix} {\bar{r}}_{n} \end{matrix}$ 进行FFT变换,获得扩频增益的同时通过频域峰值检测得到多普勒频偏的估计值:

$\begin{matrix} {\hat{f}}_{d} = \underset{f}{\arg} \max \{FFT ({\bar{r}}_{n})\} (3) \end{matrix}$

但是,当接收信噪比较低,扩频增益不足以提供一个足够高的输出SNR来保证一个可靠的多普勒频偏估计时,需要通过累加来提升接收信噪比。由于每个扩频码的信息码元都是随机的,因此需要先消除码元极性。这样,得到的多普勒频偏估计为:

$\begin{matrix} \begin{matrix} {\hat{f}}_{d} = \underset{f}{\arg} \max \{\overset{M}{\sum_{i = 1}} |FFT ({\bar{r}}_{n, i})|\} (4) \\ n \in [0, N_{c} - 1] \end{matrix} \end{matrix}$

式中: M为累加长度; N_c为扩频码长度, N_c =R_c /R_b, R_c为扩码速率, R_b为信息码元速率。

当多普勒频偏一次加速度存在时,频域信号位置会随时间的累加而发生漂移,有用信号带宽增加,常规的峰值检测处理方法无法获得准确的频偏估计,因此,需采用基于最大似然的能量检测方法来克服。由此得到的多普勒频偏估计可表示为:

式中: g( f-kB_w)为长度为 B_w的矩形窗, B_w为累加时间内信号的最大频率漂移范围。

从式(5)可以看出:由于多普勒频偏一次加速度的存在,多普勒频偏估计的精度与累加时间长度成反比;而多普勒频偏估计的可靠性与累加时间长度成正比。因此,为了实现快速、准确的多普勒频偏捕获需合理选取累加时间长度。

3 基于搜索范围预测的多普勒频偏估计算法

在设计累加时间长度时,由于累加时间长度有限,由多普勒一次加速度带来的多普勒频偏漂移有限,多个累加周期间的多普勒频偏具有很强的相关性,因此可以利用已得到的多普勒频偏估计值来缩小频偏估计的搜索范围,提高多普勒频偏估计的可靠性,从而有效缩短累加时间长度,提高估计精度。

3.1 算法提出

假设初始的多普勒频偏估计的搜索范围是 S=[ -F_max, F_max],其中 F_max为多普勒频偏的最大值。

当用相邻两个多普勒频偏估计值来预测第3个累加周期的多普勒频偏搜索范围 S'时,得到 S'为:

$\begin{matrix} \begin{matrix} S' = [\max {f_{\min} - 2 δ - 2 θ, - F_{\max}}, \\ \min {f_{\max} + 2 δ + 2 θ, F_{\max}}] (6) \end{matrix} \end{matrix}$

式中: f_min =min{ $\begin{matrix} {\hat{f}}_{d, 1} \end{matrix}$ , $\begin{matrix} {\hat{f}}_{d, 2} \end{matrix}$ }; f_max =max{ $\begin{matrix} {\hat{f}}_{d, 1} \end{matrix}$ , $\begin{matrix} {\hat{f}}_{d, 2} \end{matrix}$ }; $\begin{matrix} {\hat{f}}_{d, 1} \end{matrix}$ 和 $\begin{matrix} {\hat{f}}_{d, 2} \end{matrix}$ 为由式(5)在相邻两个累加时间周期分别得到的多普勒频偏估计值; δ是相邻的两个累加周期之间的最大多普勒漂移, δ=( aN_c R_c) /R_b; θ为多普勒频偏估计精度,当多普勒频偏估计值 $\begin{matrix} {\hat{f}}_{d} \end{matrix}$ 与真实值 f_d之间的误差满足 $\begin{matrix} |{\hat{f}}_{d} - f_{d}| \end{matrix}$ ≤ θ时,认为这次多普勒频偏估计是正确的,并且最终的检测概率也是基于此来统计的。

经过预测的搜索范围 S'的良好性质如定理1所述。

定理1 如果前两个累加时间周期的多普勒频偏估计值 $\begin{matrix} {\hat{f}}_{d, 1} \end{matrix}$ 和 $\begin{matrix} {\hat{f}}_{d, 2} \end{matrix}$ 中至少有一个是正确的,那么第3个累加时间周期的多普勒真实值 f_d,3必然满足: f_d,3∈ S'⊆ S。

证明假设第 j( j=1或 j=2)个累加时间周期的多普勒频偏估计值是正确的。那么 $\begin{matrix} {\hat{f}}_{d, j} \end{matrix}$ 显然满足 $\begin{matrix} |{\hat{f}}_{d, j} - f_{d, j}| \end{matrix}$ ≤ θ。从第 j个累加时间周期到第 j+i个累加时间周期( i=1或2),最大的频偏漂移为 iδ,即 $\begin{matrix} |f_{d, j + 2} - f_{d, j}| \end{matrix}$ ≤ iδ。考虑到估计精度,可以得到:

$\begin{matrix} \begin{matrix} f_{d, 3} \in [\max {{\hat{f}}_{d, j} - iδ - 2 θ, - F_{\max}}, \\ \min {{\hat{f}}_{d, j} + iδ + 2 θ, F_{\max}}] \end{matrix} (7) \end{matrix}$

根据以上的论述,可以发现 f_d,3∈ S'。

另外,max{ f_min -2 δ-2 θ, -F_max}≥ -F_max和min{ f_max +2 δ+2 θ, F_max}≤ F_max这两个不等式显然成立,因此 S'⊆ S。

综上所述,可以得到: f_d,3∈ S'⊆ S,证毕。

通过定理1发现,只要前2个多普勒频偏估计有1个是正确的,那么下一个真实的多普勒数值肯定在预测的搜索范围之内,也就说,前2个多普勒频偏估计值可以提供下一个累加周期的多普勒频偏先验信息,从而可以在一个较为精确的搜索范围内来判决下一次的多普勒频偏估计值。据此,设计了基于搜索范围预测的多普勒频偏估计算法。算法原理框图如图1所示。在此算法的结构中,后一级的多普勒频偏估计值的搜索范围由前一级的多普勒频偏估计结果来决定,并且为下一级的多普勒频偏估计结果做准备。

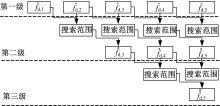	Figure Option View Download New Window
	图1 搜索范围逐级缩小的多普勒频偏估计原理框图Fig.1 Block diagram of the searching range prediction based Doppler frequency shift estimation

method

3.2 性能分析

假设在初始搜索范围内由基于FFT功率检测的多普勒频偏估计算法得到的多普勒频偏估计正确概率为 p,并且初始的搜索范围 F_max≫ δ。在这些假设条件下,考虑如下3种情形:

(1)前两个累加时间周期获得的多普勒频偏估计值{ $\begin{matrix} {\hat{f}}_{d, 1} \end{matrix}$ , $\begin{matrix} {\hat{f}}_{d, 2} \end{matrix}$ }都是正确的。根据 S'的定义,可以得到它的区间长度是5 δ+4 θ≪2 F_max。由此可见,下一次的多普勒频偏估计 $\begin{matrix} {\hat{f}}_{d, 3} \end{matrix}$ 被限制到一个相对极为精确的范围之内。并且认为在这种情况下,下一次的估计是正确的。所以在这种情况下,可以改正的错误概率是 η_c1 =p²(1 -p)。

(2)前两个多普勒频偏估计值中一个正确另一个错误。根据定理1可以发现,下一次的多普勒频偏估计被限制到一个相对于 S更小的搜索范围之内。也就是说这次正确检测概率肯定比在 S中搜索到的更高。这种情况下可以改正的错误概率是 η_c1≥0。

(3)前两个多普勒频偏估计值全是错误的。如果这两个错误同时大于或者小于下一次的真实多普勒数值,那么下一次多普勒频偏估计肯定是错误的,即便在 S范围内搜索是正确的。所以在此种情况下,误判的概率是 η_e≤(1 -p)² p。

综合以上3种情形,可以得到提出方法对多普勒频偏估计正确概率的改善为 η,且:

$\begin{matrix} \begin{matrix} η = η_{c 1} + η_{c 2} - η_{e} \geq \\ (1 - p) p^{2} - p {(1 - p)}^{2} (8) \end{matrix} \end{matrix}$

由式(8)可以看到:只要 p>0 .5,那么 η>0,也就是说,当累加时间长度能够保证多普勒频偏估计正确概率大于0.5,通过预测搜索范围就能够有效提升多普勒频偏估计的正确概率,并且正确概率逐级提高。

4 仿真结果分析

本文所采用的基本参数设置如下:扩频码速率 R_c =10 .23 Mchip/s;信息码元速率 R_b =10 kbit/s;扩频码长度 N_c =1023;累加时间长度 M=500;最大多普勒频偏 F_max =1 MHz;FFT变换点数 N_f =4096;多普勒一次加速度 a=±200 kHz/s;多普勒频偏估计精度 θ=20 kHz;信噪比 SNR=1 /σ²∈[ -40, -31] dB。

图2给出了基于搜索范围预测的多普勒捕获方法与分段补偿法和插值法的捕获概率性能曲线比较。从图中可以看到,分段补偿法在 SNR≥-38 dB时的多普勒估计性能较好;而插值法在 SNR<-38 dB时会比分段补偿法的多普勒估计性能好。但是本文提出的基于搜索范围预测的捕获方法以捕获时间为代价,使捕获概率在整个信噪比范围内得到了明显的提高。当信噪比较低时,性能提升尤为显著。比如在信噪比 SNR=-39 dB时,本文方法可以将多普勒频偏捕获的正确概率从0.58提高到0.86,将近有58%的提升,而插值法能提高到0.72,分段补偿法仅能提高到0.66。

	Figure Option View Download New Window
	图2 多普勒频偏捕获性能比较曲线Fig.2 Doppler frequency shift estimation performance of different methods

为了更清晰地表现基于搜索范围预测的多普勒频偏的捕获精度, 图3给出了 SNR=-36.5 dB下多普勒频偏捕获误差的互补累积分布函数(Complementary cumulative distribution function,CCDF)图。

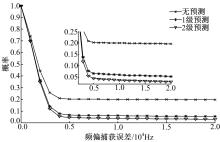	Figure Option View Download New Window
	图3 多普勒频偏捕获误差的CCDF图( SNR=-36.5 dB)Fig.3 CCDFs of the Doppler frequency shift estimation error of the proposed method ( SNR=-36.5 dB)

从图3中可以看到,随着搜索范围预测级数的增加,多普勒频偏的捕获精度显著提高。比如未采用搜索范围预测时,频偏误差大于5.0 kHz的概率是0.2,经过1级搜索范围预测处理之后,此概率下降为0.06,再经过第二级的搜索范围预测处理之后,此概率继续下降到0.04,多普勒频偏的捕获误差更趋近于零点。

5 结束语

针对极低信噪比环境下对高动态多普勒频偏的估计问题,提出了一种基于搜索范围预测的多普勒频偏估计算法。该方法利用前后信号之间多普勒频偏变化受限的特点来预测后续多普勒频偏的搜索范围,从而提高了多普勒频偏的捕获概率。仿真结果表明:该方法可以有效地提升多普勒频偏的捕获概率,并大幅减小估计误差。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Spangenberg S M, Scott I, Mclaughlin S, et al. An FFT-based approach for fast acquisition in spread spectrum communication systems[J]. Wireless Personal Communications, 2000, 13(1): 27-56. [本文引用:1] [JCR: 0.428]
[2]	Aboutanios E, Mulgrew B. Iterative frequency estimation by interpolation on Fourier coefficients[J]. IEEE Transactions on Signal Processing, 2005, 53(4): 1237-1242. [本文引用:1] [JCR: 2.813]
[3]	Reisenfeld S, Aboutanios E. A new algorithm for the estimation of frequency of a complex exponential in additive Gaussian noise[J]. IEEE Communications Letters, 2003, 7(11): 549-551. [本文引用:1] [JCR: 1.16]
[4]	吴利平, 李赞, 李建东, 等. 复杂环境下基于噪声匹配的最大多普勒频移估计[J]. 电子学报, 2011, 39(4): 842-847. Wu Li-ping, Li Zan, Li Jian-dong, et al. A maximum Doppler shift estimation based on noise matching under the complex environment[J]. Journal of Electronics, 2011, 39(4): 842-847. [本文引用:1] [CJCR: 0.087]
[5]	Dai Ling-long, Wang Zhao-cheng, Wang Jun, et al. Joint code acquisition and Doppler frequency shift estimation for GPS signals[C]∥IEEE Vehicular Technology Conference, Ottawa, 2010: 1-5. [本文引用:1]
[6]	Zakharov Y V, Baronkin V M, Tozer T C. DFT-based frequency estimators with narrow acquisition range[J]. IEE Proceedings-Communications, 2001, 148(1): 1237-1242. [本文引用:1] [JCR: 0.788]
[7]	Borio D, O'Driscoll C, Lachapelle G. Coherent, noncoherent and differentially coherent combining techniques for acquisition of new composite GNSS signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 1227-1240. [本文引用:1] [JCR: 1.299]
[8]	Yasotharan A, Thayaparan T. Strengths and limitations of the Fourier method for detecting accelerating targets by pulse Doppler radar[J]. IEE Proceedings of Radar, Sonar and Navigation, 2002, 149(2): 83-88. [本文引用:1]
[9]	Winters D W. Target motion and high range resolution profile generation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2140-2153. [本文引用:1] [JCR: 1.299]
[10]	Luo Hai-kun, Wang Yong-qing, Ma Zhi-hong, et al. A segmentation motion compensation-based long-term integration method for DSSS signal[C]∥IEEE Signal Processing Conference, Beijing, 2012: 1287-1290. [本文引用:1]
[11]	张容权, 杨建宇, 熊金涛. 基于多项相位变换的线性FMCW雷达目标加速度和速度估计方法[J]. 电子学报, 2005, 33(3): 452-455. Zhang Rong-quan, Yang Jian-yu, Xiong Jin-tao. Method for acceleration and velocity estimation of linear FMCW Radar target based on polynomial phase transform[J]. Journal of Electronics, 2005, 33(3): 452-455. [本文引用:1] [CJCR: 0.087]
[12]	蒋伟, 乐天. 基于插值的多普勒频偏和频率斜升联合估计算法[J]. 电子与信息学报, 2013, 35(1): 166-171. Jiang Wei, Le Tian. Joint estimation of Doppler frequency shift and Doppler frequency rate based on interpolation[J]. Journal of Electronics and Information Technology, 2013, 35(1): 166-171. [本文引用:1] [CJCR: 0.8805]

2000

0.428

0.0

. 2000, 13(1):27-56 DOI:10.1023/A:1008848916834

An FFT-based approach for fast acquisition in spread spectrum communication systems

1.The University of Edinburgh<br/>

This paper describes a non-coherent technique forfast acquisition of direct sequence spread spectrum(DS/SS) signals in low earth orbit (LEO) satellitecommunication scenarios. Large Doppler offsets areinherent to such environments and are likely to causemajor problems during the code acquisition phase dueto the introduced frequency ambiguity. In the presentpaper we discuss the use of a set of partialcorrelators for code phase acquisition, combined witha fast Fourier transform (FFT) for the purpose of simultaneous Doppler estimation. We will show that theuse of this architecture largely accelerates thesynchronisation process compared to conventionaltechniques over a wide range of Doppler offsets.Furthermore we discuss the implementation of azero-padded FFT that increases the frequencyresolution to such an extent, that acquisition timesidentical to scenarios without existing Doppler offsetcan be achieved.

2005

2.813

0.0

2003

1.16

0.0

2011

0.0

0.087

. 2011, 39(4):842-847

A maximum Doppler shift estimation based on noise matching under the complex environment

State Key Laboratory of ISN,Xidian University,Xi'an,Shaanxi 710071,China

According to the demand of maximum Doppler shift estimation under the urban complex channel environment,a novel maximum Doppler estimation is proposed based on noise matching.Through a low-pass filter designed (LPF) to filter the received signal,interference noise and the Doppler detector can be matched,thus the estimation performance of the maximum Doppler shift is increased effectively.Furthermore,by theoretical deduction of the best filtering ratio in Rice fading channel,two important deductions about the estimated error of proposed algorithm are presented.Monte-Carlo simulation results show that compared with the existing algorithms based on logarithmic envelope (LE) and modified covariance (MCOV),the proposed algorithm improves estimation performance by 2~5dB under the typical urban environment and low signal-noise-ratio (SNR<0dB) conditions.Therefore,proposed algorithm can ensure an accurate estimation of maximum Doppler shift and the receiving performance of mobile communication systems.

本文针对城市复杂信道环境下的最大多普勒频移估计需求,根据莱斯衰落信道中电平通过率(LCR)算法的理论推导,提出了一种基于噪声匹配的最大多普勒频移估计算法.所提算法通过对接收信号进行低通滤波处理,实现干扰噪声与多普勒检测器之间的匹配,从而有效提高最大多普勒频移的估计性能.而且基于莱斯衰落信道下最佳滤波比值的分析和推导,得到关于所提算法估计误差的两个重要推理.蒙特卡罗仿真结果表明:在低信噪比(SNR<0dB)的典型城市环境下,相比于现有的对数包络(LE)算法和修正自相关函数(MCOV)算法,所提算法提高了估计性能2~5dB,从而保证了最大多普勒频移的准确估计和移动通信系统的接收性能.

... 现有的大多普勒频移估计算法主要有基于FFT的功率谱检测算法^[1,2,3]、基于噪声匹配的算法^[4]、采用三阶段机制进行合码捕获和多普勒频偏估计的算法^[5]以及采用半分法进行迭代搜索的多普勒频偏估计算法^[6]等 ...

2010

0.0

2001

0.788

0.0

2009

1.299

0.0

... 当接收信噪比不足以保证一个可靠的多普勒频偏估计时,可通过相干或非相干累加^[7]来累积信号能量,从而有效提升接收端信噪比 ...

2002

0.0

... 但是,当多普勒频偏具有较大的动态加速度时,频域信号位置会随时间的累加而发生漂移^[8],并且最佳累加时间随加速度的增加而减小,这给多普勒频偏的准确估计带来较大难度 ...

2012

1.299

0.0

2012

0.0

2005

0.0

0.087

. 2005, 33(3):452-455

Method for acceleration and velocity estimation of linear FMCW Radar target based on polynomial phase transform

School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu,Sichuan 610054,China

In the Linear FMCW radar,the echo signal of moving target with acceleration has Doppler aberration which will degrade the detection performance and parameter estimation of target.Based on the Polynomial Phase Transform method,the paper first estimates the target's acceleration from the Doppler signal with the polynomial phase transformed,then compensates the Doppler signal with the estimated acceleration,finally,estimates the target's velocity from the compensated Doppler signal.The simulation indicates that the method can improve the detection performance and velocity estimation precision of the accelerated targets.

在线性调频连续波(LFMCW)雷达中,加速度运动目标回波存在多普勒频谱畸变现象,造成目标检测性能和参数估计精度损失.本文提出的方法首先将多普勒信号作多项相位变换,并在变换后的信号频谱中估计出目标的加速度,然后对多普勒信号进行加速度补偿,最后在补偿后的多普勒信号频谱中估计出目标速度.仿真分析表明这种方法能够以较小的运算量,达到改善加速度运动目标的检测性能和速度估计精度的目的.

2013

0.0

0.8805

. 2013, 35(1):166-171 DOI:10.3724/SP.J.1146.2012.00716

Joint estimation of Doppler frequency shift and Doppler frequency rate based on interpolation

The State Key Laboratory of Advanced Optical Communication Systems and Networks, School of EECS, Peking University, Beijing 100871, China

A joint estimation method of Doppler frequency shift and Doppler frequency rate based on interpolation is proposed for achieving fast carrier synchronization of burst in mobile satellite communication system under the circumstance of low Signal-to-Noise Ratio (SNR). In the proposed method, a coarse estimation of Doppler frequency shift and Doppler frequency rate is achieved first by a Doppler frequency rate searching combined with a traditional low-complexity frequency-estimating algorithm. The log-likelihood function of three Doppler frequency rate testing values, with the coarse estimation result as the center, is calculated and then an interpolation is taken to decide the final estimation of Doppler frequency rate. Finally, the frequency-estimating algorithm is used again to get the final estimation of Doppler frequency shift. Simulation results show that the proposed method has a low SNR threshold and an estimation performance close to Cramer-Rao Low Bound (CRLB). And it has a complexity by far the less than the max-likelihood algorithm and so is very applicable.

为解决卫星移动通信系统中突发传输在低信噪比条件下的载波快速同步问题，该文提出一种基于插值的频偏和频率斜升联合估计算法。先通过对多普勒斜升搜索结合低复杂度频偏估计获得频偏和频率斜升的粗估计结果，再以频率斜升粗估计结果为中心、计算3个频率斜升值所对应的对数似然函数并据此对频率斜升进行二次插值以获得频率斜升估计值，最后在该估计值下计算出对应的频偏估计值，完成频偏和频率斜升的联合估计。仿真结果表明，该文算法的信噪比门限较低，估计性能接近克拉美罗下界(CRLB)，而且计算复杂度远低于最大似然估计算法，非常适于实际应用。