Zernike矩快速算法的修正

引用本文

翟凤文, MuhammadAsimAzim, 王阳萍, 党建武. Zernike矩快速算法的修正. 44(6): 1860-1866
ZHAI Feng-wen, Muhammad Asim Azim, WANG Yang-ping, DANG Jian-wu. Amendment of Zernike moment fast computation. Journal of Jilin University Engineering and Technology Edition, 44(6): 1860-1866 复制到剪切板

Permissions

Zernike矩快速算法的修正

翟凤文, MuhammadAsimAzim, 王阳萍, 党建武

兰州交通大学电子与信息工程学院,兰州 730070

通信作者:党建武(1963-),男,教授,博士生导师.研究方向:智能信息处理,图像处理.E-mail:dangjw@mail.lzjtu.cn

作者简介:翟凤文(1980-),女,博士研究生.研究方向:模式识别,医学图像处理.E-mail:930843420@qq.com

基金:国家自然科学基金项目(60962004,61162016); 甘肃省自然科学基金项目(0803RJZA015); 甘肃省科技支撑计划项目(0708GKCA047);

摘要

首先对Mukundan和Ramakrishnan提出的Zernike矩快速算法进行了修正,给出了更为完整、准确的坐标变换公式。然后给出了由伪极坐标系向笛卡尔坐标系转换的方法。最后,将每一幅图像在相同阶数和重复度下的4个方向Zernike矩模值的均方差与均值的比作为评价指标,对修正前和修正后的算法以及图像预处理对Zernike矩快速算法的影响进行了综合验证。针对5幅图片,两种算法分别有5×11个评价值,实验结果表明:改进后的算法有44个评价值好于原始算法,同时也通过实验验证了多种预处理对Zernike矩的影响。

关键词: 信息处理技术; 快速算法; Zernike多项式; Zernike矩

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2014)06-1860-07

Amendment of Zernike moment fast computation

ZHAI Feng-wen, Muhammad Asim Azim, WANG Yang-ping, DANG Jian-wu

School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou 730070,China

Abstract

In this paper, first, the fast computation algorithm of Zernike moments proposed by Mukundan and Ramakrishnan was amended. Second, the transformation method from pseudo polar coordinates to the Descartes coordinates was proposed. Third, the effects of pretreatment of image on both original algorithm and the amended algorithm were tested. For each image at fixed order and fixed repetition, four moment magnitudes corresponding to the four rotations were obtained. Then the ratio of standard deviation and mean value of the four magnitudes were taken as the evaluation indicator. For comparison, the original algorithm and the amended algorithm each got 5×11 indicators from five selected images. Results show that the amended algorithm has 44 indicators exceeding that of the original algorithm.

Keyword: information process; fast computation; Zernike polynomial; Zernike moments

Show Figures

0 引言

对光学变换和几何变换具有不变性的局部特征的研究在研究图像理解、计算机视觉、图像匹配、纹理分类以及图像检索中有着非常重要的作用^{[ 1, 2, 3]}。Hu^{[ 4]}最早将矩理论用于形状识别,证明了矩的一系列性质,并提出了不变矩的概念。此后,又有学者相继提出了正交矩(Legendra矩,Zernike矩不变量)、标准矩、三维矩等概念。目前,矩特征已经广泛应用于目标识别、景物匹配、形状分析、图像正则化以及字符识别等方面^{[ 3]}。Zernike矩是正交不变矩中比较成熟的一种。Zernike矩的基是正交径向多项式,可以保证所提取的特征相关性小、冗余性小、抗噪能力强,因此,在图像处理、图像识别、机器视觉中得到了广泛的应用^{[ 5]}。Mukundan于1995年提出了Zernike矩快速算法,并得到了广泛的应用^{[ 6, 7, 8, 9]},该算法最重要的思想在于将图像数据的笛卡尔坐标系表示转化为伪极坐标系表示,替代了原始的由笛卡尔坐标系表示转化为极坐标系表示的计算方法,减少了平方、开方等计算,提高了算法效率。

为了验证该算法的有效性和准确性,本文在原文的基础上做了相应的实验和数学证明,发现Mukundan提出的坐标转换公式仅对第1和第2象限的数据是正确的,而对第3和第4象限的数据是错误的,本文对此作了相应的修正,给出了更合理的转换公式。同时,目前鲜有文献给出从伪极坐标向对应的笛卡尔坐标转换的方法,为了方便算法的理解和实际计算,本文给出了从伪极坐标向对应的笛卡尔坐标转换的具体方法。最后针对简单图像、复杂图像、二值化图像、非二值化图像、归一化图像和非归一化图像分别使用修正前和修正后的算法进行了实验,比较了二值化、归一化以及灰度处理对图像Zernike矩的影响。

1 Zernike矩的定义

Zernike矩是基于Zernike多项式的正交化函数,所利用的正交多项式集合在连续的单位圆内完备正交。

1.1 Zernike多项式

n阶 m重复度的Zernike多项式 V_nm( r, θ)定义为极坐标系中点( r, θ)的函数:

$\begin{matrix} V_{nm} (r, θ) = R_{nm} (r) e^{jmθ} (1) \end{matrix}$

式中: R_nm( r)为正交径向多项式:

$\begin{matrix} \begin{matrix} R_{nm} (r) = \overset{(n - |m| \frac{)}{2}}{\sum_{s = 0}} {(- 1)}^{s} \\ \frac{(n - s)!}{s! (\frac{n + |m|}{2} - s)! (\frac{n - |m|}{2} - s)!} r^{n - 2 s} (2) \end{matrix} \end{matrix}$

式中: n=0,1,…, ∞, n为正整数;( n-|m|)为偶数;且满足 |m|≤ n; j= $\begin{matrix} \sqrt[]{- 1} \end{matrix}$ ;( r, θ)的定义域是以原点为中心的单位圆。

Zernike多项式的正交性体现在:

$\begin{matrix} \begin{matrix} \underset{x^{2} + y^{2} \leq 1}{\int \int} V_{nm}^{*} (x, y) V_{pq} (x, y) dxdy = \\ \{\begin{matrix} \frac{π}{n + 1}, n = p; m = q \\ 0, 其他 \end{matrix} (3) \end{matrix} \end{matrix}$

式中:*表示取共轭; $\begin{matrix} V_{nm}^{*} \end{matrix}$ ( x, y)是 V_pq( x, y)的共轭。

1.2 Zernike矩

Zernike矩的概念首先由Teague于1980年引入^{[ 7]},对于某一密度函数为 f( x, y)的图像,其 n阶 m重复度的Zernike矩定义为:

$\begin{matrix} \begin{matrix} Z_{nm} = \frac{n + 1}{π} \underset{x^{2} + y^{2} \leq 1}{\int \int} V_{nm}^{*} (x, y) f (x, y) dxdy \\ (4) \end{matrix} \end{matrix}$

其极坐标形式为:

$\begin{matrix} Z_{nm} = \frac{n + 1}{π} \overset{2 π}{\int_{0}} \overset{1}{\int_{0}} V_{nm}^{*} (r, θ) f (r, θ) rdrdθ (5) \end{matrix}$

由式(5)知,对于一幅二维图像,其Zernike矩 Z_nm为一复数,将其实部和虚部分别记为 C_nm和 S_nm,其中:

$\begin{matrix} \begin{matrix} C_{nm} = \frac{2 n + 1}{π} \overset{1}{\int_{0}} \overset{2 π}{\int_{0}} R_{nm} (r) \cos (mθ) f (r, θ) rdrdθ (6) \\ S_{nm} = - \frac{2 n + 1}{π} \overset{1}{\int_{0}} \overset{2 π}{\int_{0}} R_{nm} (r) \sin (mθ) f (r, θ) rdrdθ (7) \end{matrix} \end{matrix}$

根据正交性,式(5)的反变换为:

$\begin{matrix} \begin{matrix} f (r, θ) \approx \frac{C_{n 0}}{2} R_{n 0} (r) + \\ \overset{M}{\sum_{n = 1}} \sum_{m > 0} (C_{nm} \cos (mθ) + S_{nm} \sin (mθ)) R_{nm} (r) (8) \end{matrix} \end{matrix}$

式中: M表示所需使用的矩的最高阶数,由于不可能给出所有阶的Zernike矩,所以一般 M取到40就可以较好地反变换出原始图像。

2 Zernike矩快速算法

由于实际问题中所需处理的图像通常为数字图像,因而需要将式(6)(7)离散化,又由于Zernike多项式在单位圆内正交,因此需要将所考虑的图像转换为单位圆内的极坐标形式^{[ 7]}。Mukundan和Ramakrishnan在文献[6]中指出计算Zernike矩需要将笛卡尔坐标系转换为极坐标系,此过程涉及大量的平方和开方计算,效率较低,因此提出了一种将笛卡尔坐标系转换为伪极坐标系的方法,并在此基础上,给出了Zernike矩的快速算法。

2.1 笛卡尔坐标系转换为伪极坐标系

Mukundan提出的转换思想如图1所示。

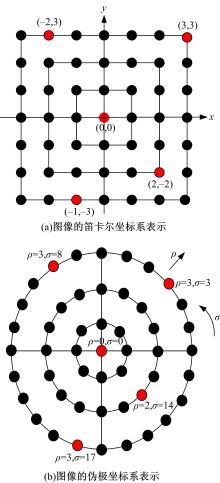	Figure Option View Download New Window
	图1 笛卡尔坐标系转化为伪极坐标系示意图Fig.1 Schematic diagram for converting cartesian coor-dinate system to pseudo polar coordinates system

Mukundan和Ramakrishnan指出,对于任一 N×N的图像 f( x, y),不失一般性,令坐标原点位于图像的中心,则 -N/2≤( x, y)≤ -N/2。对于任一像素点( x, y),引入2个参数 ρ和 σ,它们唯一地对应像素点( x, y),其定义为:

$\begin{matrix} ρ = \max (|x|, |y|) \end{matrix}$

若 ρ=|x|,则:

$\begin{matrix} σ = 2 \times (ρ - x) \times \frac{y}{|y|} + \frac{x \times y}{ρ} \end{matrix}$

若 ρ=|y|,则:

$\begin{matrix} σ = 2 \times y - \frac{x \times y}{ρ} (9) \end{matrix}$

对于对应的点( x, y)有:

$\begin{matrix} f (ρ, θ) = f (x, y) (10) \end{matrix}$

Mukundan指出, ρ在径向方向上取值从1到 N/2,在圆周方向上 σ取值从1到8 ρ,由图1可知 f( ρ, θ)和 f( x, y)是一一对应的,并且 σ是大于0的。

但是,可以发现,对于图1(a)中的像素点(0,0)、(3,3)和(-2,3)分别根据式(9)计算可得其伪极坐标对应为图1(b)中的(0,0)、(3,3)和(3,8)。而对于像素点(-1,-3)和(2,-2),分别应用式(9)进行计算可得其伪极坐标为(3,-7)和(2,-2),与 σ取值从1到8 ρ是相矛盾的,并且按照式(9), σ的取值是从 -4 ρ到4 ρ,而非1到8 ρ。由上面的分析可知,式(9)对第1象限和第2象限内的像素点,转换结果是正确的,而对于第3和第4象限的像素点,转换的结果是错误的。这是该转换方式的一个纰漏。

根据Mukundan的转换思想,本文对式(9)进行修正,得到式(11),该转换过程分为两步:

Step 1

若 ρ=|x|,则:

σ_t =2 ×( ρ-x) × $\begin{matrix} \frac{y}{|y|} \end{matrix}$ + $\begin{matrix} \frac{x \times y}{ρ} \end{matrix}$

若 ρ=|y|,则:

σ_t =2 ×y- $\begin{matrix} \frac{x \times y}{ρ} \end{matrix}$

Step 2

若 σ_t≥0,则:

σ=σ_t

否则:

$\begin{matrix} σ = 8 ρ + σ_{t} (11) \end{matrix}$

对于对应的点( x, y)有:

$\begin{matrix} f (ρ, θ) = f (x, y) (12) \end{matrix}$

由式(11)进行由笛卡尔坐标系向伪极坐标系的转换,可以验证转换的正确性。此时 ρ取值从1到 N/2, σ取值从1到8 ρ,真正符合了Mukundan的转换思想。

2.2 Zernike矩快速算法

由参数 ρ, σ可定义相应的伪极坐标^{[ 1]}:

r= $\begin{matrix} \frac{2 ρ}{N} \end{matrix}$ , θ= $\begin{matrix} \frac{πσ}{4 ρ} \end{matrix}$

式中: r∈[0,1]; θ∈[0,2π],此时

d r= $\begin{matrix} \frac{2}{N} \end{matrix}$ ,d θ= $\begin{matrix} \frac{π}{4 ρ} \end{matrix}$ , rd rd θ= $\begin{matrix} \frac{π}{N^{2}} \end{matrix}$

经过该转换,式(6)(7)可以分别表示成如下的离散形式:

$\begin{matrix} \begin{matrix} C_{nm} = \frac{2 n + 2}{N^{2}} \overset{N / 2}{\sum_{ρ = 0}} R_{nm} \frac{2 ρ}{N} \overset{8 ρ}{\sum_{σ = 0}} \cos (\frac{πmσ}{4 ρ}) f (ρ, σ) (13) \\ S_{nm} = - \frac{2 n + 2}{N^{2}} \overset{N / 2}{\sum_{ρ = 0}} R_{nm} \frac{2 ρ}{N} \overset{8 ρ}{\sum_{σ = 0}} \sin (\frac{πmσ}{4 ρ}) f (ρ, σ) (14) \\ Z_{nm} = C_{nm} + j S_{nm} (15) \\ |Z_{nm}| = \sqrt[]{C_{nm}^{2} + S_{nm}^{2}} (16) \end{matrix} \end{matrix}$

设原始图像的Zernike矩为 Z_nm,则旋转角度 θ后,旋转图像的Zernike矩为 Z'_nm, Z_nm与 Z'_nm存在下面的关系:

Z'_nm=Z_nm $\begin{matrix} e^{- jm θ_{0}} \end{matrix}$

$\begin{matrix} |Z'_{nm}| \end{matrix}$ = $\begin{matrix} |Z_{nm} e^{- jm θ_{0}}| \end{matrix}$ = $\begin{matrix} |Z_{nm}| \end{matrix}$

因此图像Zernike矩的模存在旋转不变性,此特性常被用作图像区域特征的特征描述子。

由式(13)(14)知,在计算 Z_nm的实部 C_nm和虚部 S_nm时,要使用伪极坐标下的 f( ρ, σ),此时需要找到原始笛卡尔坐标系下对应像素的灰度值 f( x, y),没有文献给出这个过程,因此影响了读者对该算法的理解。在此给出下面的伪代码以求得 f( ρ, σ):

function get_f(ρ,σ)

{

if(σ<ρ+1)

{ x=ρ;

y=σ; }

if(σ>ρ&&σ<2*ρ+1)

{y=ρ;

x=ρ-σ%ρ;}

if(σ>2*ρ&&σ<3*ρ+1)

{y=ρ;

x=-σ%ρ;}

if(σ>3*ρ&&σ<4*ρ+1)

{y=ρ-σ%ρ;

x=-ρ;}

if(σ>4*ρ&&σ<5*ρ+1)

{y=-σ%ρ;

x=-ρ;}

if(σ>5*ρ&&σ<6*ρ+1)

{y=-ρ;

x=-(ρ-σ%ρ);}

if(σ>6*ρ&&σ< 7*ρ+1)

{y=-ρ;

x=σ%ρ;}

if (σ>7*ρ&&σ< 8*ρ)

{y=-(ρ-σ%ρ);

x=ρ;}

f(ρ,σ)=f(x,y);

}

需要注意的是,这里要求原始图像的坐标原点在图像的中心,因此,假设图像的尺寸为 N×N,则 -N/2≤ x, y≤ -N/2。

3 实验结果分析

3.1 实验结果

实验用图如图2所示。为了验证修正后算法的正确性,并验证预处理对图像Zernike矩的影响,本文分别按照原始算法和改进后的算法对归一化的图像a、未归一化的图像a、归一化的图像b、未归一化的图像b以及二值化并归一化的图像b,计算其旋转0°、90°、180°和270°后的Zernike矩的模。实验结果如表1和表2所示:

	Figure Option View Download New Window
	图2 实验用图Fig.2 Experimental images

3.2 实验结果分析

表1 原始Zernike矩快速算法实验结果 Table 1 The original Zernike moments fast computation results

Z_nm	旋转	(0,0)	(1,1)	(2,0)	(2,2)	(3,1)	(3,3)	(4,0)	(4,2)	(4,4)	(7,3)	(7,5)
a归一化	0°	1.366947	0.003427	0.102413	0.007300	0.012901	0.008564	0.087812	0.016915	0.000216	0.043701	0.019723
	90°	1.365829	0.011021	0.106630	0.010870	0.021420	0.003194	0.096533	0.033611	0.007034	0.006593	0.013763
	180°	1.350613	0.003332	0.116665	0.006178	0.006555	0.010249	0.055355	0.006804	0.000302	0.075980	0.019864
	270°	1.350324	0.003361	0.117167	0.006200	0.006544	0.010312	0.055553	0.006820	0.000281	0.076324	0.019990
a未归一化	0°	348.571512	0.874007	26.115185	1.861545	3.289890	2.183910	22.392115	4.313239	0.055101	11.143686	5.029317
	90°	348.286343	2.810286	27.190484	2.771811	5.462065	0.814452	24.615820	8.570730	1.793628	1.681174	3.509626
	180°	344.406405	0.849643	29.749584	1.575503	1.671561	2.613400	14.115577	1.734908	0.077107	19.374922	5.065252
	270°	344.332712	0.857008	29.877533	1.580941	1.668744	2.629536	14.166099	1.739008	0.071558	19.462611	5.097472
b归一化	0°	1.211954	0.074318	0.033443	0.026664	0.085260	0.095172	0.294679	0.121776	0.031186	0.043652	0.005656
	90°	1.131358	0.012475	0.021916	0.012111	0.004946	0.010427	0.459169	0.145918	0.084070	0.008799	0.003752
	180°	1.175794	0.041809	0.015270	0.024609	0.068517	0.105112	0.374905	0.050300	0.030865	124059	0.103890
	270°	1.255480	0.047180	0.028510	0.040204	0.035171	0.022244	0.209286	0.055066	0.082130	0.083920	0.096770
b未归一化	0°	309.048692	18.951154	8.528250	6.799343	21.741338	24.268795	75.143232	31.052892	7.952393	11.131287	1.442209
	90°	288.496675	3.181088	5.588442	3.088417	1.261214	2.658917	117.087759	37.209018	21.437774	2.243711	0.956799
	180°	299.828143	10.661323	3.894222	6.275399	17.471892	26.803605	95.600457	12.826586	7.870608	31.634923	26.491923
	270°	320.147861	12.030815	7.270716	10.252102	8.968511	5.672275	53.368295	14.041720	20.943090	21.399592	24.676412
b 二值化归一化	0°	1.214601	0.080561	0.036035	0.035937	0.055779	0.089790	0.334025	0.139314	0.044446	0.049720	0.024857
	90°	1.124403	0.000629	0.000739	0.012313	0.018139	0.013663	0.519392	0.160008	0.120681	0.004535	0.003747
	180°	1.156278	0.054314	0.019224	0.030869	0.061384	0.108539	0.437515	0.067979	0.014617	0.130101	0.159363
	270°	1.245854	0.054447	0.055773	0.031258	0.035124	0.019523	0.250520	0.076788	0.088880	0.102201	0.120484

表1 原始Zernike矩快速算法实验结果 Table 1 The original Zernike moments fast computation results

表2 修正后的Zernike矩快速算法实验结果 Table 2 Amended Zernike moments fast computation results

Z_nm	旋转	(0,0)	(1,1)	(2,0)	(2,2)	(3,1)	(3,3)	(4,0)	(4,2)	(4,4)	(7,3)	(7,5)
a归一化	0°	2.718190	0.008717	0.218022	0.013081	0.007362	0.016040	0.142911	0.022631	0.000158	0.115737	0.036623
	90°	2.717940	0.012025	0.218228	0.009067	0.031310	0.003278	0.142249	0.021152	0.000115	0.013261	0.010085
	180°	2.717075	0.005158	0.219829	0.013739	0.006328	0.021010	0.143043	0.024531	0.000140	0.119984	0.041432
	270°	2.716534	0.005242	0.220830	0.013806	0.006440	0.021091	0.143610	0.024642	0.000115	0.120507	0.041658
a未归一化	0°	693.138574	2.222712	55.595596	3.335561	1.877225	4.090216	36.442339	5.770888	0.040318	29.512812	9.338839
	90°	693.074743	3.066447	55.648034	2.312202	7.984044	0.835864	36.273531	5.393735	0.029196	3.381433	2.571762
	180°	692.854290	1.315266	56.056091	3.503557	1.613570	5.357605	36.476362	6.255319	0.035692	30.596012	10.565143
	270°	692.716355	1.336677	56.311351	3.520586	1.642171	5.378312	36.620543	6.283833	0.029237	30.729196	10.622790
b归一化	0°	2.387630	0.107821	0.046095	0.051088	0.165699	0.207306	0.671311	0.176025	0.001785	0.155095	0.106417
	90°	2.386818	0.026338	0.047507	0.028597	0.054662	0.004260	0.669156	0.199087	0.000502	0.082333	0.094353
	180°	2.386756	0.124560	0.047464	0.048676	0.139199	0.195050	0.667723	0.172009	0.000314	0.181125	0.086585
	270°	2.386878	0.042747	0.046635	0.030632	0.028699	0.017380	0.670357	0.202773	0.002631	0.103658	0.106945
b未归一化	0°	608.846387	27.494408	11.753445	13.027428	42.253272	52.863029	171.184147	44.886248	0.455294	39.549311	27.136391
	90°	608.638623	6.716339	12.114354	7.292230	13.938823	1.086256	170.635065	50.767226	0.127946	20.994979	24.060000
	180°	608.623690	31.762885	12.103776	12.412362	35.495669	49.737727	170.270031	43.862364	0.080055	46.186726	22.079209
	270°	608.654764	10.900588	11.891778	7.811284	7.318184	4.431870	170.941975	51.707005	0.670816	26.432871	27.271012
b 二值化归一化	0°	2.370534	0.126650	0.051724	0.066446	0.128358	0.205185	0.772360	0.211384	0.031158	0.166589	0.191753
	90°	2.369885	0.046985	0.053371	0.043871	0.068054	0.001401	0.772077	0.235292	0.030473	0.087387	0.118752
	180°	2.370078	0.143429	0.054076	0.064150	0.102653	0.193396	0.771000	0.207352	0.029802	0.194637	0.170580
	270°	2.370651	0.063179	0.052727	0.046733	0.041740	0.011370	0.771082	0.238405	0.032461	0.108349	0.131335

表2 修正后的Zernike矩快速算法实验结果 Table 2 Amended Zernike moments fast computation results

首先分析表1和表2中对应的数据, 表1中的数据只有一小部分能够体现Zernike矩的旋转不变性,而表2中则有一大部分可以体现Zernike矩的旋转不变性。比如,对于归一化的图像a,其4阶Zernike矩 Z₄₂,在旋转0°、90°、180°和270°时, Z₄₂值分别为0.016915,0.033611,0.006804,0.006820,是跳跃的;而在表2中,分别为0.022631,0.021152,0.024531,0.024642,体现出了Zernike矩的旋转不变性。Zernike多项式只有在连续的单位圆内是正交的,而一幅图像的数据是离散的,因此图像的Zernike矩的模值不可能保证绝对的旋转不变性,而且有时可能会产生较大的跳跃。

为了比较修正后的算法和原始算法在表达图像不变性方面的优劣,分别按照原始算法和修正后的算法,计算了每一幅图片在相同阶数( n)和重复度( m)下旋转0°、90°、180°和270°时,所得的Zernike矩模的标准差与均值的比,如表3和表4所示,标准差与均值的比越小表示不变性越好。

表4中用粗体标记的数据比表3中对应位置数据的数值大,这是由于Zernike矩的数学特性造成的,理论上,Zernike多项式必须是在连续的单位圆内才正交。表4中其余的数据可以说明修正后的Zernike矩快速算法比原始算法在性能上有了很大的提高。同时可以发现,图像归一化与否对Zernike矩模值的旋转不变性没有太明显的影响,而图像二值化却可以减小图像旋转各角度后Zernike矩模值的标准差与均值的比。图像简单与否与Zernike矩模值的旋转不变性并没有明显的联系。

表3 原始Zernike矩快速算法所得同一幅图片旋转0°、90°、180°和270°后Zernike矩的标准差与均值的比 Table 3 Ratio between the standard deviation and the mean value of the Zernike moments for images after rotated 0°、90°、180°and 270° using original algorithm

表4 修正后的Zernike矩快速算法所得同一幅图片旋转0°、90°、180°和270°后Zernike矩的标准差与均值的比 Table 4 Ratio between the standard deviation and the mean value of the Zernike moments for images after rotated 0°、90°、180°and 270° using amended algorithm

4 结束语

对Mukundan提出的Zernike矩快速算法原理进行了详细的讨论,发现了该算法在由笛卡尔坐标系向伪极坐标系转换的过程中存在的纰漏,给出了相应的修正,并给出了由伪极坐标系向笛卡尔坐标系转换的伪代码。

通过实验验证了改进后算法的正确性和有效性。同时,实验比较了归一化和二值化,以及图像的复杂度对图像Zernike矩模值旋转不变性的影响。当前对Zernike矩及其相位的研究也越来越深入^{[ 4, 10, 11]},本文可以对Zernike矩的研究和应用提供一定的参考。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chen Z, Sun S K. A Zernike moment phase based descriptor for local image representation and matching[J]. IEEE Transactions on Image Processing, 2010, 19(1): 205-219. [本文引用:1] [JCR: 3.199]
[2]	Mikolajczyk K, Tuytelaars T, Schmid C, et al. A comparison of affine region detectors[J]. International Journal of Computer Vision, 2005, 65(1): 43-72. [本文引用:1] [JCR: 3.623]
[3]	郭哲, 张艳宁, 林增刚. 基于扩展二维不变矩的三维人脸特征提取[J]. 吉林大学学报: 工学版, 2012, 42(2): 446-450. Guo Zhe, Zhang Yan-ning, Lin Zeng-gang. 3D face feature extraction based on extended 2D invariant moments[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(2): 446-450. [本文引用:1] [CJCR: 0.701]
[4]	Hu M, Visual K. Pattern recognition by moment invariant[J]. IEEE Transactions on Information Theory, 1962, 12(8): 179-187. [本文引用:2] [JCR: 2.621]
[5]	Ye Bin, Peng Jia-xiong. Analysis and improvement of invariance of Zernike moments[J]. Infrared and Laser Engineering, 2003, 32(1): 37-41. [本文引用:1] [CJCR: 0.883]
[6]	Mukundan R, Ramakrishnan K R. Fast computation of Legendre and Zernike moments[J]. Pattern Recognition, 1995, 28(9): 1433-1442. [本文引用:1] [JCR: 2.632]
[7]	Teague M R. Image analysis via the general theory of moments[J]. Journal of the Optical Society of America, 1980, 70(8): 920-930. [本文引用:2]
[8]	徐旦华, 辜嘉, 李松毅, 等. Zernike 矩的快速算法[J]. 东南大学学报: 自然科学版, 2002, 132(12): 189-192. Xu Dan-hua, Gu Jia, Li Song-yi, et al. Fast algorithm for computation of Zernike moments[J]. Journal of Southeast University (Natural Science Edition), 2002, 132(12): 189-192. [本文引用:1] [CJCR: 0.756]
[9]	http://scholar.google.com.hk/scholar?q=+Mukundan+R+%2C+Ramakrishnan. [本文引用:1]
[10]	Li S, Lee M C, Pun C M. Complex Zernike moments features for shape-based image retrieval[J]. IEEE Transactions on Systems, Man and Cybernetics-Part A: Systems and Humans, 2009, 39(1): 227-237. [本文引用:1] [JCR: 2.183]
[11]	Singh C, Walia E, Mittal N. Rotation invariant complex Zernike moments features and their applications to human face and character recognition[J]. IET Computer Vision, 2011, 5(5): 255-265. [本文引用:1] [JCR: 0.636]

2010

3.199

0.0

... 可定义相应的伪极坐标^[1]: ...

2005

3.623

0.0

. 2005, 65(1):43-72 DOI:10.1007/s11263-005-3848-x

A comparison of affine region detectors

1.University of Oxford OX1 3PJ Oxford United Kingdom OX1 3PJ Oxford United Kingdom<br/>2.University of Leuven Kasteelpark Arenberg 10 3001 Leuven Belgium Kasteelpark Arenberg 10 3001 Leuven Belgium<br/>3.Czech Technical University Karlovo Namesti 13 121 35 Prague Czech Republic Karlovo Namesti 13 121 35 Prague Czech Republic<br/>4.INRIA, GRAVIR-CNRS 655, av. de l'Europe 38330 Montbonnot France 655, av. de l'Europe 38330 Montbonnot France<br/>

The paper gives a snapshot of the state of the art in affine covariant region detectors, and compares their performance on a set of test images under varying imaging conditions. Six types of detectors are included: detectors based on affine normalization around Harris (Mikolajczyk and Schmid, 2002; Schaffalitzky and Zisserman, 2002) and Hessian points (Mikolajczyk and Schmid, 2002), a detector of ‘maximally stable extremal regions', proposed by Matas et al. (2002); an edge-based region detector (Tuytelaars and Van Gool, 1999) and a detector based on intensity extrema (Tuytelaars and Van Gool, 2000), and a detector of ‘salient regions', proposed by Kadir, Zisserman and Brady (2004). The performance is measured against changes in viewpoint, scale, illumination, defocus and image compression.

The objective of this paper is also to establish a reference test set of images and performance software, so that future detectors can be evaluated in the same framework.

2012

0.0

0.701

. 2012, 42(2):446-450

3D face feature extraction based on extended 2D invariant moments

School of Computer Science, Northwestern Polytechnical University, Xi'an 710129, China

A novel 3D face feature extraction method based on 2D extended strategy is proposed. Zernike Moment Invariants of multi-pose 3D face model, which have scale, translation and rotational invariance, are extracted after preprocessing and grid normalization of 3D face models. A suitable feature evaluation measure is then proposed based on the parameter space and is applied to the evaluation of Zernike Moment Invariants and depth feature. Experimental results based on multi-pose 3D face database show that the proposed method is robust to pose variant and has a separability.

将二维不变矩理论和算法扩展应用于三维人脸特征提取的研究,在对三维人脸模型进行预处理及网格归一化的基础上,建立了具有平移、比例和旋转不变性的三维人脸模型的Zernike矩不变量特征表示,并基于距离可分性设计了一种特征评价测度,对所提特征和深度特征进行了对比评价。多姿态三维人脸数据库的实验结果表明,三维人脸模型的Zernike矩不变量特征具有对不同姿态人脸模型鲁棒、可分性强等优点。

... 目前,矩特征已经广泛应用于目标识别、景物匹配、形状分析、图像正则化以及字符识别等方面^[3] ...

1962

2.621

0.0

... Hu^[4]最早将矩理论用于形状识别,证明了矩的一系列性质,并提出了不变矩的概念 ...

... 当前对Zernike矩及其相位的研究也越来越深入^[4,10,11],本文可以对Zernike矩的研究和应用提供一定的参考 ...

2003

0.0

0.883

. 2003, 32(1):37-41

Analysis and improvement of invariance of Zernike moments

在分析了Zernike矩不变性后,提出了一种基于图像整个区域形状描述算子的改进Zernike矩.改进的Zernike矩不仅具有旋转不变性,而且还具有改进前不具有的比例不变性.试验结果证明,和改进前的Zernike矩相比,改进后的Zernike矩具有更好的不变特征,可用作基于区域的形状描述算子.

Abstract：

An improved Zernike moment used as a region-based shape descriptor is presented. The improved Zernike moment has not only rotation invariance, but also scale invariance that the original Zernike moment does not have. The experimental results show that the improved Zernike moment has better invariant poperties and can be used as region-based shape descriptor.

... Zernike矩的基是正交径向多项式,可以保证所提取的特征相关性小、冗余性小、抗噪能力强,因此,在图像处理、图像识别、机器视觉中得到了广泛的应用^[5] ...

1995

2.632

0.0

. 1995, 28(9):null-null

Fast computation of Legendre and Zernike moments

1980

0.0

... 2 Zernike矩Zernike矩的概念首先由Teague于1980年引入^[7],对于某一密度函数为f(x,y)的图像,其n阶m重复度的Zernike矩定义为: ...

... 2 Zernike矩快速算法由于实际问题中所需处理的图像通常为数字图像,因而需要将式(6)(7)离散化,又由于Zernike多项式在单位圆内正交,因此需要将所考虑的图像转换为单位圆内的极坐标形式^[7] ...

2002

0.0

0.756

. 2002, 132(12):189-192

Fast algorithm for computation of Zernike moments

给出了Zernike矩求解的一种快速算法.利用Zernike多项式迭代性质,找出了Zernike正交矩之间的内在关系,这样,高阶的Zernike矩可由低价的Zernike矩求出, 再在Chan等人提出的关于一维几何矩有效算法的基础上,得出了一种快速算法.与已有方法相比,该算法大大减少了求解过程中的乘法次数,降低了计算复杂度,从而提高了运算速度和效率;并可以有效用于模式识别、图像分析及重建等领域中.

0.0

2009

2.183

0.0

2011

0.636

0.0