作者简介:张梦楠(1986-),男,博士研究生.研究方向:时滞系统稳定性控制.E-mail:09111017@bjtu.edu.cn
针对列车制动过程中,减速度易受线路条件和闸瓦摩擦因数的干扰而难以准确测量,传统闭环控制方法也无法消除输入时滞和非线性对系统性能造成的影响的问题,本文基于电空制动系统工作原理,建立了具有输入时滞的非线性城轨列车制动模型。为消除模型中非线性、时滞及有界扰动的影响,基于反推技术和Krasovskii泛函算子,设计了鲁棒制动控制器。通过Lyapunov-Krasovskii 方法,证明了闭环系统对于系统中的有界扰动为输入状态稳定的(ISS)。为验证鲁棒控制器的正确性,利用Matlab仿真软件对制动模型进行了仿真。结果表明:所提算法不仅改善了制动系统性能,并且对系统中扰动和输入时滞具有良好的鲁棒性。
Braking deceleration accuracy and velocity accuracy are two important indexes to measure the brake system performance. However, in real braking, the deceleration cannot be accurately measured because that it is easily affected by the line conditions and brake shoe coefficient. Conventional closed-loop control method cannot deal with the phenomena of input delay and nonlinearity in the system. According to the operation principle of the electro-pneumatic brake system, a nonlinear brake model with input delay is built. To deal with the nonlinearity, input delay and bounded disturbances in the system, a robust brake controller based on backstepping technique and Krasovskii functional operators is designed. By Lyapunov-Krasovskii method, the close-loop system is proved to be Input-State-Stable (ISS) with respect to bounded disturbances. To validate correctness of the robust controller, the brake model is simulated on Matlab. Results demonstrate that the proposed model not only improves the brake system performance, but also is robust to disturbances and input delay in the brake system.
城轨列车制动系统的性能对于保障列车高速、安全运行具有十分重要的作用。制动减速度精度和速度精度是衡量制动控制系统性能的重要物理指标[1, 2]。实际制动控制中, 制动控制器通过控制减速度的直接方法或者追踪参考速度曲线的间接策略, 实现高性能的制动系统。
由于制动系统本身存在时滞, 会对闭环系统稳定性造成破坏, 因此制动系统通常采取开环控制策略。然而, 线路阻力的不确定性、闸瓦摩擦系数的非线性及制动系统所受随机扰动都会对制动系统带来不利影响。开环控制方法由于无法消除这些因素的影响[1], 从而在一定程度上降低了制动系统的性能。
为克服上述问题, 许多专家和学者从理论和工程上提出了改进方法。制动控制器设计通常采用模糊控制的方法处理系统自身的非线性和大延时等问题[3]。为消除系统的输入时滞, 有研究人员在控制器设计中采用了基于Smith预估器的PID控制策略, 该控制器在提高制动减速度精度的同时保证了闭环系统的稳定性[4]。由于列车运行中要受到横向、垂向和纵向的随机扰动, 实际应用中很难测量减速度数值。为解决这一问题, 文献[5]中, 对减速度传感器的位置和滤波算法进行了改进, 用以减小测量中的噪声并取得了一定效果。但是, 实际制动系统设计中对于这些问题仍然缺乏统一的可行标准, 因此直接控制制动减速度不仅不能充分保证行车安全, 而且会使控制问题更为复杂化。
列车制动系统本质上是具有下三角结构的非线性输入时滞系统, 可以通过经典的反推方法使系统镇定。但是由于输入时滞系统只能用过去的状态控制系统的当前时刻[6, 7], 所以这一经典算法与输入时滞系统相结合时受到很大限制。Krstic基于PDE提出了反推方法镇定具有输入时滞和状态时滞的线性系统[8, 9]。Mazenc将经典的反推控制策略扩展到了具有输入时滞和状态时滞的非线性系统中[10, 11]。
然而上述方法由于缺少对实际背景的分析, 其应用受到限制。本文提出了一种鲁棒反推制动控制器, 用以消除制动过程中闸瓦摩擦因数的非线性特性、输入时滞、线路阻力及系统随机扰动的影响。首先, 建立了描述制动系统动态特性的能观数学模型。所提模型克服了传统模型中制动减速度无法测量的缺点。其次, 采取追踪参考运行速度曲线的方法提高了制动控制精度。算法上, 基于Krasovskii泛函算子, 研究了当前时刻状态与过去时刻状态之间的关系, 并结合反推技术设计了制动控制器。最后, 利用Matlab仿真软件对制动系统进行了数值仿真。仿真结果表明该算法可以显著改善制动系统性能, 并对系统中时滞和扰动具有良好的鲁棒性。
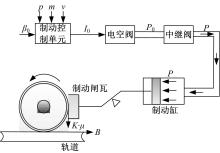
电空制动系统的信号流和单轮物理模型如图1所示。图中, 信号流包括制动微制动控制单元(MBCU)、电空阀、中继阀和基础制动装置。首先, MBCU根据制动减速度参考值 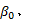


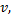
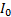
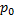

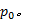
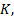


列车所需制动力计算公式为[13]:

式中: 

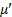


式中: 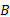
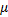


式中: 
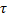
在制动系统中, 引起该延时的因素很多:压力空气的传播速度, MBCU算法运算和分配制动减速度的时间, 电空阀、中继阀的响应时间等[4, 12]。
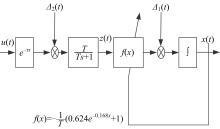
列车制动过程中, 闸瓦摩擦因数的大小通常与列车运行速度有关, 其大小是速度的非线性函数, 可以由指数形式表示:
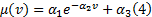
式中: 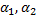
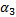
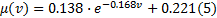
实际制动控制中, 理想的闸瓦摩擦系数设计值为 
基于上述分析, 制动系统非线性数学模型为:
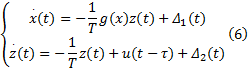
式中: 
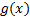
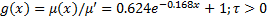

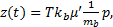
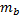
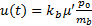
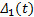
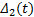
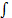
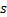
列车制动控制器设计的思想是使列车实际的运行速度追踪参考速度曲线, 从而使速度追踪误差、加速度误差均收敛于原点附近的邻域内, 进而提高制动系统精度和行车的安全性。
假设1 参考速度信号 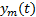
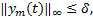
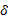
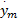
假设2 列车的运行速度、制动缸压力信号是有界的, 则式(6)中状态变量 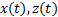



定义速度追踪误差为 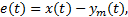

制动控制器设计目标为:设计状态反馈控制器 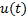
定义(7)中第一个方程为无延时子系统, 
Step1 为了使无延时子系统稳定, 选择Lyapunov函数 
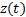
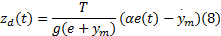
式中: 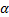
令 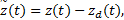
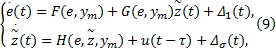
式中: 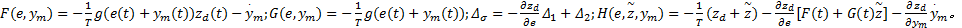
基于Lyapunov函数 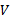

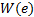

Step2 由反推控制思想, 实际控制输入 
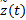



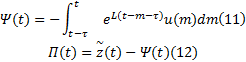
式中: 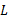
引理1 针对非线性输入时滞系统(9), 设计控制器

则Krasovskii泛函算子 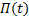
证明 Krasovskii泛函算子 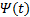
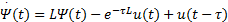
将控制器和 

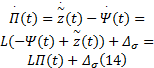
由于 
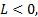
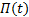
提出可镇定条件引理2和延时假设3。
引理2 针对误差系统(9), 列车制动速度 
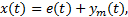
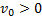

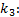

式中: 
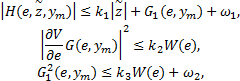
式中: 
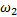

证明 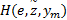
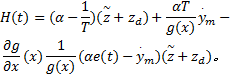
因此, 根据式(15)中定义, 可得:

式中: 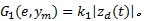
进一步由几何不等式可得:
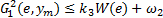
根据式(15)中 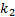

上述引理得证。
假设3 制动系统时滞 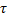

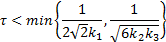
假设1和假设2是控制系统的一般假设, 假设3为对系统时滞的约束。
定理1 当城轨列车制动控制系统满足假设1~3, 根据误差系统(9)设计制动控制器:
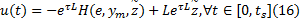
式中: 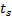
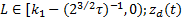
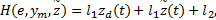
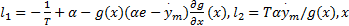

首先, 引入Krasovskii泛函算子 

定义 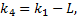
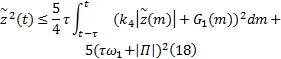
由几何不等式(18)可进一步表示为:
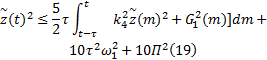
那么, 基于假设3和式(18), 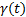

选取参数 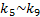

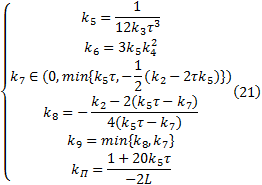
注1 根据假设3, 可得 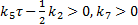

基于Krasovskii泛函算子, 引入Lyapunov-Krasovskii泛函如下:
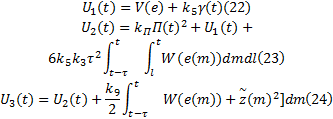
显然, 根据文献[6, 18], 泛函 
基于引理2和式(21)中参数定义可得:
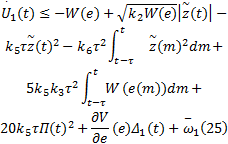
式中: 
根据参数(21)和 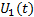

进一步, 由式(26)可得下列不等式:

所以, 最终Lyapunov-Krasovskii泛函 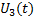

式中: 
通过交换积分次序, 可以得到下列不等式:
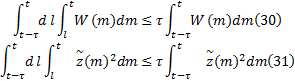
再由几何不等式 


那么根据式(32), 可得误差系统(9)在闭环控制器(16)下, 对于有界扰动 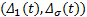
为验证鲁棒控制算法的有效性, 在Matlab/Simulink环境下进行了具有随机扰动的列车制动控制数值仿真。仿真中, 为体现算法的优势, 将该算法与基于Smith预估器的PID控制器进行了比较。仿真参数如表1所示。
| 表1 仿真参数 Table 1 Simulation Parameters |
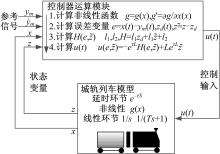
为提高算法效率, 降低运算复杂度, 控制器实现流程如图3所示。
由文献[14-16]中数据, 仿真中线路阻力 
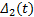
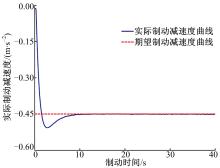
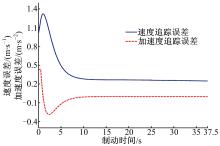
在随机扰动和控制器的作用下, 城轨列车追踪误差曲线、实际制动减速度曲线见图5、图6。
图5显示了鲁棒反推控制器克服了系统中时滞、非线性和随机扰动的影响, 获得了良好的追踪效果。在停车点附近, 其速度误差小于0.2 m/s, 加速度误差接近于0。图6显示实际制动减速度最终收敛到-0.45 m/s2, 表明制动系统获得了很高的制动减速度精度。整个制动过程中, 制动减速度振荡幅度很小, 符合最大制动减速度的约束, 且牵引单元不工作, 从而保证了列车运行的平稳性[16]。
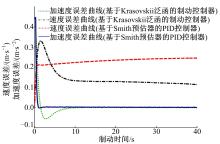
由于系统存在输入延时, 制动单元可以采取基于Smith预估器的PID控制算法进行控制[4], 其追踪误差的比较曲线如图7所示。
图7表示, 制动减速度方面PID控制器的快速性更好。但是, 由于PID控制器只能实现对制动减速度的追踪控制, 因此其速度追踪误差随时间逐渐增大, 整体制动性能不高。另外, 基于Smith预估器的控制器对制动系统时滞更为敏感。当系统的实际时滞偏离设计值时, 系统的品质会严重下降。图8为系统实际时滞τ =0.5 s情况下, 系统的制动减速度误差曲线变化情况的比较。显然, 基于Krasovskii泛函的制动控制器对系统延时具有更好的鲁棒性, 且控制系统的品质更为稳定。
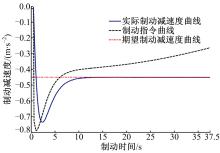
在实际列车运行过程中, 可能会遇到理想制动曲线初速度小于实际制动初始速度的紧急情况。这种条件下, 采用基于Smith预估器设计的PID控制策略不能充分保障行车安全。本文中的算法可以克服制动初始状态的偏差, 使列车实际运行速度追踪理想的速度曲线。仿真中, 参考曲线制动初始速度为17 m/s。图9为紧急情况下追踪的误差曲线, 图10为制动指令曲线和实际制动减速度曲线。
图9表示反推制动控制器在轮轨黏着允许的前提下, 可以克服制动初速度不一致的影响, 并且获得较好的追踪效果。在停车点附近, 其速度追踪误差小于0.25 m/s, 加速度追踪误差接近于0。紧急制动工况下, 其制动力要大于常用制动工况下的制动力。图10中, 实际制动减速度不超过-1 m/s2, 且收敛于期望值。整个制动过程中, 制动控制器发出的控制指令不超过最大制动减速度的限制, 且牵引单元不工作, 保证了列车运行的平稳性[16]。制动指令曲线存在0.3 s的输入时滞。从而说明反推控制器消除了输入时滞对系统稳定性造成的影响。
(1)根据电空制动系统工作原理建立了具有输入时滞的非线性能观制动模型。所提模型不仅反映了制动过程中受到的动态阻力, 而且描述了制动系统控制信号所受随机扰动的动态过程。
(2)基于反推控制策略和Krasovskii泛函算子设计了鲁棒制动控制器。控制器基于预测思想, 将误差信号表示为两个与延时相关的Krasovskii泛函算子, 且其中一个算子对扰动为输入状态稳定。
(3)从常用制动以及紧急制动两种工况下对控制模型进行了仿真, 并与PID控制策略进行了比较。结果表明, 该算法不仅可提高制动系统性能, 并对外界扰动、输入时滞有良好的鲁棒性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|