作者简介:王伟(1982-),男,工程师,博士研究生.研究方向:地质工程及桥梁结构计算.E-mail:wangwei1982718@sohu.com
以Maple软件为平台,提出了利用求解微分方程组对柔性墩台进行内力计算的方法。此方法先将桥梁各墩台分别视为一整体考虑,根据各节点处的协调变形关系和力的平衡条件建立墩台各计算单元的微分关系。再通过将整联墩台视为一整体考虑,根据混凝土的收缩、徐变以及温度影响力在各节点处产生的横向位移确定各墩台之间的微分关系。最后通过联立微分方程组并求解,得到各墩台内力变化的函数解析式。与目前广泛使用的“集成刚度法”相比,本文方法计算步骤简捷方便,计算结果精确可靠。
Using Maple software as the platform, a method is proposed to calculate the internal force of flexible pier by solving the differential equation set. In this method, first, each bridge pier is considered as a whole, and the differential relationship of each calculation unit of the pier is established according to the coordinating deformation of each node and the force equilibrium condition. Then, all the bridge piers are considered as a whole, and the differential relationships among the piers are established according to the lateral displacement produced by shrinkage, the creep of concrete and the temperature influence on each node. Finally, by simultaneously solving the differential equation set, the internal force functional analytical formula of each pier was obtained. Compared to the currently used integrated stiffness method, the proposed calculation method has the advantages of simple and convenient, and the result is more precise and reliable.
在柔性墩台的计算中, 通常将柔性墩视为下端固定、上端铰接的超静定梁进行分析, 桩基础的内力则常采用弹性地基梁法求解。由于水平力的作用, 墩身的内力计算按照墩顶及墩底均为弹性约束考虑, 其水平力在各墩上的分配问题通常采用集成刚度法计算。集成刚度法在计算时需要根据不同条件进行查表取值, 计算量非常大, 计算过程十分繁琐, 增大了误差出现的几率[1, 2]。
近些年对于柔性墩台施工技术、病害防治的研究较多, 但是对于内力计算方法的探索却极为有限[3]。国内方面, 朱彦鹏等[4]采用幂级数法求解了桩的内力及变形的具体计算式; 张耀辉等[5]根据弹性支座的特性提出将整个桥按超静定体系进行分析计算; 郗蔚东[6]采用位移法对墩台桩基础进行了有限元法的计算; 吴宜凤等[7]提出了二维动态规划法计算桩柱式墩台的内力, 取得了良好的效果; 马缤辉等[8]推导了在水平力作用下的弹性地基梁位移及内力的解析解; 周绍烈[9]提出采用直接刚度法进行水平力的计算, 该方法便于计算机编程; 徐玉中等[10]提出采用位置传导法计算梁桥墩台的水平力。另外, 还有众多学者对内力计算方法进行探索和尝试[11, 12, 13, 14, 15, 16, 17]。国外方面, Poulos[18, 19]采用相互作用系数方法分析水平荷载作用下的群桩问题; Pak[20]基于虚拟桩模型建立了均质地基中横向受荷桩的求解方法。这些研究虽然通过实验数据、数值分析等方法简化了计算步骤, 但是分析过程需要大量的数理知识, 不利于实际工程中的应用。
本文以基础工程[1]中的文克尔假定将桩墩视为一整体考虑, 利用支座、墩身和基桩的基本微分方程, 建立常微分方程组。同时将整联墩台整体分析, 通过平衡条件、边界条件和协调条件, 建立墩台的常微分方程组。最后利用Maple软件求出各墩台的横向位移 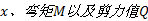
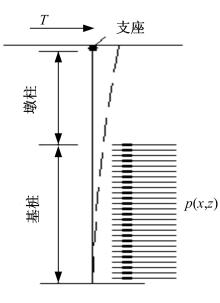
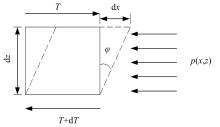
将柔性墩台的支座、墩柱和基桩视为一个整体考虑, 对结构进行内力分析时应遵循静力平衡、变形协调和本构关系的原则, 基于“ m” 法中的文克尔假定推导其微分方程式。桥梁上部结构的水平荷载通过支座和墩台连接组成超静定结构, 在水平力作用下, 柔性墩台的受力变形简图见图1。取单元进行受力分析如图2所示, 假定其位移以向右为正, 转角顺时针偏转为正, 由水平方向静力平衡条件可得:
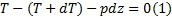
简化后得:
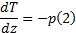
由材料力学[3]可知, 在荷载作用下支座剪力 
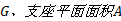
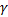
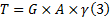
式中:剪切应变 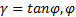
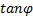
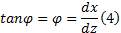
将式(3)代入式(2)可得:
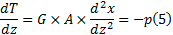
由于支座侧向不存在均布荷载, 因此 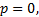
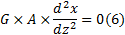
由材料力学[2]和基础工程[1]可知, 墩身和基桩的挠曲微分方程为:
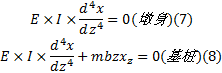
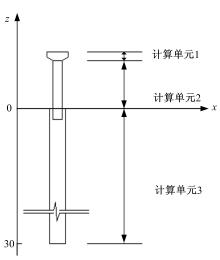
对柔性墩台进行整体分析时, 由于墩台在支座、墩身和基桩各部位的受力不同, 因此需对墩台进行计算单元划分。由于基桩受到横向的土抗力, 而墩身与支座无横向抗力, 因此在均布荷载不连续处, 可作为分段点。桥梁上部结构水平力通过弹性支座传递, 而支座和墩身的内力微分方程不同, 因此可将支座处作为计算单元的分段点。墩台的计算单元划分见图3。
墩台的墩身与基桩的微分方程不同, 而墩身与基桩的直径也有变化。当集中力作用在墩柱上时, 剪力 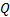
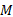
柔性墩台的水平力通过弹性支座传递到各墩台上, 在混凝土收缩、徐变以及温度上升或下降的作用下, 使墩台产生一定的水平位移。根据墩台计算单元的划分, 可将各单元节点处作为边界条件。边界条件的建立应遵循以下原则:①固定端处:转角 
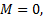
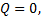
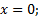
对单个墩台的变形协调条件可由其计算单元节点处的变形及静力平衡条件确定。在水平力作用下, 各单元节点处的变形及转角相等并连续, 节点上下剪力、弯矩相等并连续。即:转角 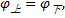
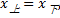
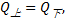
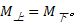
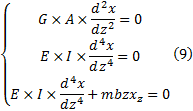
以墩台桩顶标高为零点, 桩长为 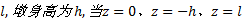
将整桥桥墩作为整体进行受力分析, 可视每个墩台为一个计算单元, 在水平力的作用下, 各单元节点处的变形连续, 整桥遵循力矩平衡条件, 即:相邻两墩台的水平位移 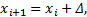
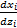
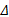
在温度影响力作用下, 桥梁上部结构由于混凝土的收缩、膨胀在各支座处将产生变形和位移, 其位移计算式如下:
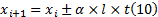
式中: 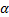
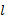
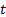
根据式(10)可得到相邻两墩台之间横向位移的协调关系, 将各墩顶由温度升降引起的横向位移与其他边界条件和协调条件共同建立的微分方程式联立组成微分方程组, 可以求解方程组中的所有未知常数, 再将所得各常数代入各墩台的微分方程, 即可得到各墩台受力和变形的解析式。
结合参考文献[2]中的算例一, 应用Maple中求解微分方程组的方法对柔性墩台的内力进行计算。
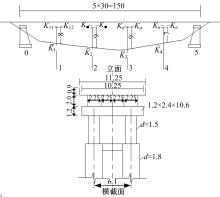
已知一连续桥面简支梁桥, 0号台与5号台为活动支座, 其余各墩均为板式橡胶支座。下部结构采用双柱式圆柱墩, 直径为1.5 m, 钻孔桩直径为1.8 m, 长为30 m。墩柱与桩均为C25混凝土, Ⅱ 级钢筋, 两柱中心距为6.10 m。当地月平均最高温度为35 ℃, 月平均最低温度为0 ℃。1号墩墩身长8 m, 2、3号墩墩身长9 m, 4号墩墩身长7 m。施工温度为15 ℃~25 ℃。桥梁立面及横截面布置如图5所示。
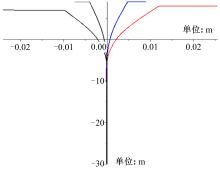
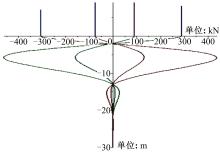
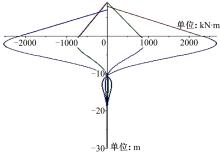
经过Maple计算, 得到各墩台在混凝土收缩、徐变以及温度影响力作用下的各墩台的横向位移、剪力和弯矩的函数解析式, 其变化曲线见图6~图8。
将微分方程组法得到的各墩台计算结果与算例结果进行比较, 其对比结果见表1。通过比较可以看出, 各墩的水平力结果分别相差了0.3%、0.3%、0.4%、0.4%, 各墩的弯矩结果分别相差了0.5%、0.4%、0.6%、0.2%。两种方法得出的结果相差不大, 可以说明用微分方程组法求解柔性墩台的内力是可行的, 同时由于采用了Maple计算绘图软件, 利用其强大的求解微分方程组的计算功能, 精简了计算步骤, 使墩台的内力计算更加简便快捷, 降低了由于查表计算产生的误差。此外, 通过计算得到的墩台内力解析式, 可求得任意深度下墩台的剪力、弯矩以及横向位移, 更加方便于实际工程中应用, 因此可以在柔性墩台内力计算中推广使用。
| 表1 计算结果对比 Table 1 Comparison of calculation result |
(1)运用微分方程组法计算得到的位移、弯矩和剪力的解析式和图形更加直观、准确, 同时计算过程中省略了查表手算等过程, 与集成刚度法相比更为简便快捷。
(2)经过计算得到的解析解与算例中的数值解相比, 更为精确。通过解析式还可得到任意深度下的剪力、弯矩和横向位移。
(3)通过将单个墩台和整联墩台分别作为一个整体考虑, 根据变形协调和力的平衡建立边界条件, 可以得到整个桥梁各墩台支座、墩柱和基桩以及墩台与墩台之间的微分关系, 因此在计算时确定正确的边界条件是关键。
(4)本文在计算时虽然没有计入制动力, 但通过计算结果的比较, 验证了本文方法在柔性墩台内力计算中应用的可行性, 具有一定的推广意义。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|