随着混合动力技术的出现, 液压挖掘机的全局功率匹配有望实现, 通过引入辅助动力源, 解决动力源-泵功率匹配环节对泵排量调节的依赖。国外各大挖掘机研究机构和制造商如日本的小松、神户制钢所和神户建机, 德国的利勃海尔, 美国的卡特彼勒等率先开展了相关的研究工作并取得了阶段性成果^{[1, 2, 3, 4]}。国内一些工程机械企业及科研院校, 也开始了混合动力挖掘机关键技术的研究工作, 2009年三一重工推出了国内首台履带式混合动力挖掘机, 随后詹阳重工也推出了轮式混合动力液压挖掘机^[5], 浙江大学最早开展了混合动力挖掘机控制策略的仿真和台架试验研究^{[6, 7, 8]}。这些阶段性成果集中体现在挖掘机混合动力结构布置和节能算法研究方面, 因无法实时准确地计算出负载功率需求, 从而主动合理的分配主、辅动力源的功率输出, 使得混合动力总成与负载功率匹配的效果并不理想。作为挖掘机重要能量转换元件的变量泵, 结构复杂, 制造精密, 虽有学者对其特性开展了研究^{[9, 10, 11, 12]}, 但目前还没有一个有效实用的模型可以实时准确地计算出液压泵吸收功率, 即负载需求功率。

为解决在变量泵几何参数未知的情况下, 实时准确地计算挖掘机负载需求功率的问题, 鉴于支持向量机(SVM)^{[13, 14]}理论在非线性系统建模及预测控制中的成功运用^{[15, 16]}, 本文提出采用实验建模的方法, 基于最小二乘支持向量机^{[17, 18]}(LS-SVM)算法建立恒功率变量泵的功率预测模型。为使模型对作业环境具有更好的适用性, 并采用液压挖掘机实际挖掘作业时采集的载荷谱训练模型, 采用网格搜索法^[19]和交叉验证法^[17]优化模型参数对模型的准确性进行验证。

SVM是一种基于统计学习理论和结构风险最小化原则的机器学习方法, 它成功地解决了非线性函数的回归问题。为了避免求解SVM中耗时的二次规划问题, Suykens等^[17]于1999年提出了改进的LS-SVM, 以等式约束代替标准SVM算法的不等式约束, 提高了求解速度和收敛精度。

对于给定样本集(x_i, y_i)(i=1, 2, …, l), x_i∈ Rⁿ为输入数据, y_i∈ R为输出数据。设对样本集进行拟合的函数形式为:

式中:非线性映射φ :Rⁿ→ R^nh将输入数据映射到一个高维特征空间, 权向量ω ∈ R^nh, 偏置量b∈ R。

为求解y(x), 定义目标函数如下:

式中:γ 为正实数; ζ _i为松弛变量。

定义Lagrange函数:

式中:α _i为拉格朗日乘子, 根据KKT条件

消去ω 和ζ _i得到优化问题的解析解:

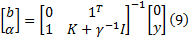
式中:α = ; 1= ; 方阵K满足K_ij=φ φ (x_j), i, j=1, 2, …, l。

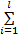
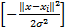
进而求得最小二乘模型y(x)= α _iK(x, x_i)+b, 核函数K(x, x_i)是满足Mercer条件的任意对称函数, 常用核函数有:①线性核:K(x, x_i)=x· x_i; ②高斯核(又称径向基核):K(x, x_i)=exp ; ③多项式核:K(x, x_i)= , m=1, 2, …, N。

作为研究对象的并联式混合动力液压挖掘机动力总成结构如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 并联式混合动力液压挖掘机结构示意Fig.1 Structure of parallel hybrid excavator

主动力源发动机与辅助动力源ISG(Integrated starter generator)电机同轴联接共同驱动液压泵, 其功率匹配实现条件为:

式中:k为效率修正系数; P_pump为液压泵的吸收功率。

液压泵功率计算公式为:

式中:p为泵出口压力; q为液压泵排量; n_e为发动机转速。

2.1 液压挖掘机双联式变量泵工作过程分析

双联式变量泵采用了恒功率和负流量控制技术, 图2为其液压原理图。图中1为负流量控制阀杆, 液压挖掘机多路换向阀(图2中未画出)中位回油道上设有节流孔, 液压油流经节流孔产生压差, 将节流孔前的压力P_i引至负流量控制阀杆, 用以调节液压泵排量。负流量控制系统可有效减少空流损失和节流损失。2为液压交叉和电控阀杆, 泵1输出压力P₁和泵2输出压力P₂以及极限载荷控制压力P_sv(先导压力P₃经电磁阀5后的二次压力)共同作用在阀杆2上。以左泵负载增加为例说明液压泵的变量过程。负载增加时P₁增大, 作用在阀杆2上的力随之增大并克服弹簧力推动伺服阀杆3右移, 伺服阀左路导通, 因伺服缸4柱塞左右面积不等, 故在P₁作用下柱塞右移, 斜盘摆角变小, 左泵排量减小。同时伺服柱塞通过回馈杆带动伺服阀套右移关闭伺服阀, 达到新的平衡。而由式(11)表述的泵的吸收功率在动作前后基本保持恒定。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 变量泵液压原理图Fig.2 Hydraulic schematic diagram of pump

通过上述分析可知, 作业过程中对泵排量起决定作用的因素为负流量控制压力P_i, 泵1输出压力P₁, 泵2输出压力P₂以及极限载荷控制压力P_sv。将泵视为多输入单输出系统, 采用改进的LS-SVM算法建立变量泵排量预测模型。

2.2 泵功率预测模型的建立

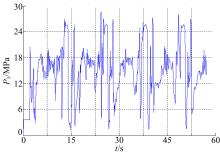
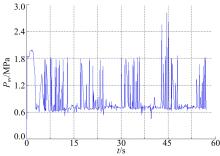
为使模型对作业环境具有更好的适应性, 采用液压挖掘机实际挖掘作业时采集的载荷谱作为训练样本, 以泵输出压力、负流量控制压力和极限载荷控制压力作为训练模型的输入, 以泵的排量作为输出建立所需模型。为验证训练模型的通用性, 采集挖掘原生土和清理河道两种工况的样本数据作为测试数据, 选取统计性能较好的高斯核作为模型的核函数。建模过程如下:①输入训练集, 即以P₁、P₂、P_i、P_sv作为输入, q作为输出。训练集各属性参数如图3所示; ②优选核函数的核宽度σ 和惩罚因子γ , 由LS-SVM算法求解参数α 和b, 得到所需预测模型; ③输入测试集, 使用得到的预测模型对泵排量进行预测。支持向量机算法的训练速度受训练集的样本数的制约, 样本中只有支持向量对训练结果产生关键影响, 为确定适合的训练集样本数, 对于特定的训练数据, 分别以3种不同的采样频率对其采样, 组成了3组试验训练集, 训练结果如表1所示。

表1

Table 1

表1(Table 1)

表1 训练结果 Table 1 Training results 训练集 样本数 训练时间/s MSE 准确率/% 1 300 20 0.23 63.27 2 600 60 0.0021 97.41 3 1200 130 0.0007 97.89

表1 训练结果 Table 1 Training results

综合训练时间和准确率来看, 试验训练集2更适合作为训练集。对于LS-SVM算法, 核宽度σ 和惩罚因子γ 的选择至关重要, 这两个参数很大程度上决定了模型的精度。本文采用网格搜索法和交叉验证法对[σ , γ ]参数对进行选择和寻优。设定σ 和γ 的区间分别为[2^-10, 2⁸]和[2^-10, 2⁷], 步距为0.1, 遍历区间对所有的[σ , γ ]参数对进行搜索; 对于所选取的一对[σ , γ ], 采用K-CV方法对训练集进行测试, 得到对应的平均均方根误差MSE_cv, 最终取使得MSE_cv最小的一组[σ , γ ]为模型参数。通过寻优, 得到最佳模型参数为核宽度σ =3.0314, 惩罚因子γ =1。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 训练集各属性参数(a) 泵1输出压力P1Fig.3 Attribute parameters of training set

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 训练集各属性参数(b) 泵2输出压力P2Fig.3 Attribute parameters of training set

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 训练集各属性参数(c) 负流量控制压力PiFig.3 Attribute parameters of training set

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 训练集各属性参数(d) 极限载荷控制压力PsvFig.3 Attribute parameters of training set

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 训练集各属性参数(e) 泵排量qFig.3 Attribute parameters of training set

2.3 结果分析

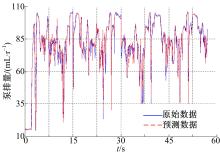
泵排量的LS-SVM模型预测值与采集的实验真实值对比如图4~图6所示, 其中图4为模型对训练集的预测结果, 预测数据与实测真值的MSE为0.0021, 预测的平均准确率为97.41%, 可见模型对于训练数据的拟合精度非常高。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 模型对训练集2的预测结果Fig.4 Prediction result of training set 2

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 模型对测试集1的预测结果Fig.5 Prediction result of training set 1

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 模型对测试集2的预测结果Fig.6 Prediction result of test set 2

图5是模型对测试集1(重载工况)的预测结果, 预测数据与实测真值的MSE为0.0062, 预测的平均准确率为95.38%。图6是模型对测试集2(经济工况)的预测结果, 预测数据与实测真值的MSE为0.0087, 预测的平均准确率为96.82%。

提出了一种采用LS-SVM算法对液压挖掘机标准作业工况下液压负载功率进行预测的方法。以变量泵排量的主要影响参数为输入, 泵排量为输出建立预测模型。实验结果表明, 用所建立的模型预测的平均准确率在95%以上, 且具有良好的泛化能力, 能准确有效地预测变量泵排量, 满足计算泵功率的精度要求, 可用于基于混合动力技术的液压挖掘机功率匹配。