引用本文
于振环, 张娜, 刘顺安. 基于流-固耦合的车辆减振器动态非线性仿真分析. 45(1): 16-21
YU Zhen-huan, ZHANG Na, LIU Shun-an. Simulation analysis of dynamic nonlinear characteristics of vehicle shock absorber based on fluid-structure interaction. Journal of Jilin University Engineering and Technology Edition, 45(1): 16-21  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于流-固耦合的车辆减振器动态非线性仿真分析
于振环1, 张娜2, 刘顺安1
1.吉林大学 机械科学与工程学院,长春 130022
2.长春汽车工业高等专科学校 机电工程学院,长春 130011

作者简介:于振环(1979-),男,博士研究生.研究方向:车辆动力学.E-mail:yuzhenhuan@163.com

基金:国家自然科学基金项目(50475011)
摘要

基于流-固耦合有限元方法,利用ADINA软件建立了高精度的叠加节流阀片有限元网格模型和流场有限元网格模型,并在ADINA软件后处理模块中进行求解分析,得到了减振器阻尼力-速度分段特性、示功特性、阀系内部的压力场和速度场特性,分析了减振器阀系动态非线性特性。结果表明:在高速减振器油的冲击下,阀系内部区域的压力场变化明显;达到开阀压力时,油液流动速度呈现跳跃变化,使得阻尼通道压力迅速变化。这说明叠加节流阀片有限元网格模型和流场有限元网格模型的精度对仿真结果影响最大。在流-固耦合计算中考虑了流体湍流流动、阀片接触和大位移变形,尽量使仿真模型与物理模型保持一致,试验结果与仿真结果吻合较好。

关键词: 车辆工程; 油-气混合型减振器; 阻尼力动态响应特性; 流-固耦合; 有限元分析
中图分类号:U463.33 文献标志码:A 文章编号:1671-5497(2015)01-0016-06
Simulation analysis of dynamic nonlinear characteristics of vehicle shock absorber based on fluid-structure interaction
YU Zhen-huan1, ZHANG Na2, LIU Shun-an1
1.College of Mechanical Science and Engineering, Jilin University,Changchun 130022,China
2.Mechanical and Engineering Department,Changchun Automobile Industry Institute,Changchun 130011,China
Abstract

Using software ADINA, accurate finite element mesh models of the superposition throttle slice and fluid field are established based on the Fluid-Structure Interaction (FSI) method. The velocity property, the indicator diagram, internal pressure field and velocity field of the shock absorber are obtained using the post-processing module of ADINA. The nonlinear dynamic characteristics are analyzed. Results show that, under high-speed impact of the shock absorber oil, the pressure field inside the valves changes significantly. When reaching the valve-opening pressure, the fluid velocity suddenly jumps, making the pressure change rapidly in the damping channel. The finite element mesh models of the superposition throttle slice and fluid field significantly influence the accuracy of the simulation results. The FSI model is close to the physical reality because the consideration of the turbulent flow of oil, the contact slip and large deflection of the throttle slices. The simulation results are in good agreement with the experimental results.

Keyword: vehicle engineering; gas-pressurized hydraulic damper; dynamic response characteristics of damping force; fluid-structure interaction(FSI); finite element analysis
引言

减振器是车辆悬架系统的主要组成元件, 由活塞与节流阀片组成的减振器阀系是减振器产生阻尼作用的重要元件, 活塞孔的大小、节流阀片的数量以及调整垫圈的厚度决定了阻尼特性[1], 所以, 如何将以上三者合理匹配是保证减振器特性的关键。现阶段使用半经验公式+试验的方法对减振器进行开发[2, 3], 使开发周期长, 而且不容易得出阀片开度、流量系数等关键参数值[4, 5, 6]。本文基于流-固耦合有限元分析, 利用ADINA软件建立了减振器流-固耦合动力学模型, 得到了减振器动态响应特性、流体压力场特性、减振器阻尼力-速度曲线、压差-流量特性以及示功图, 对减振器进行台架试验, 并将试验结果与仿真结果进行了对比分析。

1 减振器阀系结构原理及阻尼力

特性图1为减振器复原阀系结构图, 当活塞杆受车身的带动而做拉伸运动时, 减振器产生阻尼力衰减车身振动。当车身的速度相对较小时, 减振器工作缸内的压差也相对较小, 减振器油经多槽阀片缝隙由上腔流入下腔, 此时叠加节流阀片没有变形量, 阻尼力由多槽阀片缝隙产生; 当车身速度相对较大时, 减振器工作缸内的压差变大, 这时叠加节流阀片开始变形, 此时阻尼力大小取决于叠加节流阀片的变形量; 当车身速度变到更大时, 叠加节流阀片变形量达到最大值, 此时阻尼力大小由活塞孔决定。

图1 减振器复原阀系结构图 1-螺母; 2-垫圈; 3-补偿阀; 4-活塞; 5-多槽阀片; 6-五片节流阀片; 7-调整垫圈; 8-阀片Fig.1 Structure diagram of rebound valve of shock absorber

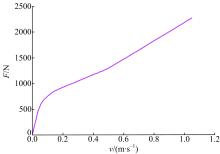
图2为减振器复原阀系阻尼力特性, 减振器阻尼力会产生三段特性, 即低速段、中速段和高速段。低速段为多片节流阀片未开启时, 减振器阻尼力由多槽阀片上的多槽面积决定, 此时油液为稳态流动; 中速段为多片节流阀片未全部打开时, 当活塞移动速度变大, 减振器工作缸内压差会突然变大, 此时阻尼力也突然变大, 叠加节流阀片开启, 此时为开阀点(图中0.05~0.15 m/s之间), 叠加节流阀片的变形刚度和活塞上的段差对开阀点的位置起着决定性的作用, 此时减振器油开始做湍流运动; 高速段为叠加节流阀片全部打开时, 活塞运动速度继续增大, 此时减振器阻尼力由活塞孔直径大小和阀片变形刚度决定, 而且活塞孔直径大小决定了中、高速段曲线斜率的大小。每段阻尼力特性都由多种不同因素所决定, 但之间又互相联系、互相影响, 只有认真考虑它们之间的关系, 才能开发出准确的减振器阻尼力特性。

图2 减振器复原阀系阻尼力特性Fig.2 Damping characteristics of rebound valve of shock absorber

2 FSI有限元分析
2.1 FSI有限元基本原理

FSI有限元分析可用来解决流体与固体之间的运动状态的问题, 它的基本原理是[7]:既要满足流体耦合动力学方程和运动学方程, 又要满足固体耦合动力学方程和运动学方程, 将流体和固体之间耦合起来, 运动学条件为:

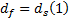
动力学条件为:

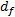
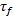
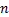
式中: 和 分别代表流体和固体的边界位移; 和 分别代表流体和固体应力; 为单位外法线矢量。

由运动学条件可导出流体速度条件为:

2.2 基于ADINA的流-固耦合有限元分析

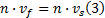
利用有限元FSI基本理论解决以下问题:

(1)流-固耦合面上相互作用力的准确传递。在ADINA软件中, 固体模型与流体模型是分别建立的, 分别在两个模型的耦合面上定义边界条件来实现相互之间的耦合计算, 流体和固体的网格不需要完全一致[8], 只要达到一定容差即可。流-固耦合面上流体节点位移可以由附近固体节点位移的插值得到, 而固体节点可以通过对周围流体应力积分而得到:

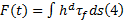
式中: 为固体虚位移。

(2)由固体变形而引起的流体网格移动问题。目前使用的方法是将欧拉方程映射到ALE(Arbitrary Lagrangian Euleria)。在ADINA软件中, 固体变形决定了流-固耦合边界上流体节点的位移和速度, 通过求解Laplace方程可以得到由此引起的流体体积的改变量。除此之外, 定义Leader-Follower点可以对模型中流体边界的网格进行人为控制。

(3)对整个耦合系统求解。ADINA软件有两种方法, 即迭代解法和直接解法。直接解法是把流体模型及固体模型放在同一矩阵中求解, 有限元方程如下:

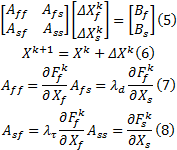
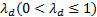
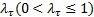
式中: 为位移松驰因子; 为应力松驰因子。直接解法对于解决计算量不是很大的非接触瞬态模型时, 具有很高的精准度。

流体分为不可压缩流体和可压缩流体[9]。如果不考虑减振器油的热量变化, 减振器油的密度变化量趋于零, 所以减振器油可以定义为不可压缩流体。

3 减振器FSI有限元模型

减振器阀系特性决定减振器特性, 因此需要建立减振器阀系固体模型和阀系流场模型, 删除不参与计算的结构, 如:将工作缸、贮油缸等做刚体处理。减振器复原阀系与压缩阀系类似, 本文仅讨论减振器复原阀系的FSI模型和求解结果。

3.1 复原阀系流场有限元模型

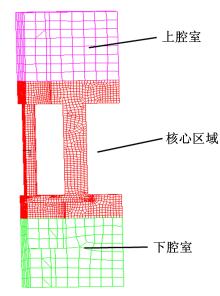
建立如图1所示的复原阀系流场模型。考虑到计算机CPU的计算能力及求解时间, 建立复原阀系1/4流场有限元模型, 如图3所示。流体模型为8节点六面体单元, 计算变量插值时具有良好的二阶精度。根据有限元计算精度要求, 将复原阀系流场分为三部分, 即上腔室、核心区域和下腔室。上腔室为液体入口处, 上腔室和下腔室与核心区域(活塞、节流通道和节流阀片)流场相比变化不大, 因此可以设置较大单位有限元单元, 以减少计算时间。活塞、节流通道和节流阀片部分流场是减振器核心工作区域, 流场运动剧烈, 为保证流-固耦合面计算时相对位移 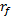在公差范围内, 需要划分较小单位体积的有限单元。为提高计算的收敛性, 在活塞与节流阀片之间建立液体流通缝隙, 面积等于多槽阀片节流面积。ADINA软件能对FSI面上的网格自适应耦合计算, 与多求解器流-固耦合方法相比, 建立网格效率更高、更方便, 计算收敛性更好。

图3 流场有限元模型Fig.3 Finite element model of flow field

3.2 复原阀系固体有限元模型

考虑对称性, 建立1/4复原阀系模型, 如图4所示。模型结构包括叠加阀片模型、阀片接触模型、阀片与活塞面接触模型, 如图5所示。为保证流场网格变形后厚度大于零, 阀片与活塞接触距离设为40 μ m。阀片与阀片和阀片与活塞之间的边界定义为接触, 一共设为5个接触对。为保证流-固耦合面密度相容性, 复原阀系模型采用8节点六面体单元划分。

图4 固体有限元模型Fig.4 Finite element model of solid

图5 阀片与活塞接触模型Fig.5 Contact model between piston and valve

4 减振器FSI的求解策略
4.1 流-固耦合区域

尽管ADINA软件能够进行流-固耦合面网格自适应计算, 但流-固耦合面的空间位置应保持一致, 以提高收敛性。

4.2 初始条件及边界条件

固体模型里有5个阀片组成一组多片节流阀片, 每片厚度为0.203 mm、直径为20 mm。固体分析类型为隐式动态法。为保证仿真流场变化与试验环境相符, 流场初始速度设置为由静止开始加载的正弦波, 如图6所示。流场模型出口处不做任何边界条件设置, ADINA软件默认出口处压力值为零。工作缸为刚性材料, 设置为wall。

图6 入口速度时间Fig.6 Inlet velocity-time curve

4.3 提升流-固耦合求解能力

阀系流场模型和固体模型均使用六面体网格划分, 虽能提高求解精度, 但求解时间较长。因此需要提升求解能力。

(1)设置求解收敛因子。力收敛因子和位移收敛因子的选择范围是0~1。二者决定收敛速度的快慢, 通过实际操作以及以往的经验, 本文力收敛因子选择0.5, 位移收敛因子选择0.6。

(2)只考虑流场节流片处的动网格, 其余部分不考虑动网格移动。

(3)时间步长应在保证收敛性的前提下适当减小, 以控制求解效率。

(4)仿真周期为1/4正弦波, 以减小计算时间。

(5)对阀系模型进行简化, 消除对减振器阻尼特性影响较小的特征, 如:节流阀片在运动中的摩擦、减振器油在运动过程中产生的热学效应以及油液的压缩特性。

5 减振器仿真分析与试验

本文的试验设备为Instron公司生产PC63M液压试验台, 试验结果采用多个减振器试验结果的平均值, 以减少试验误差。

试验台激振速度分别为0.05、0.1、0.3、0.6、1 m/s。计算在DELL XPS17上完成。

5.1 流-固耦合仿真与试验

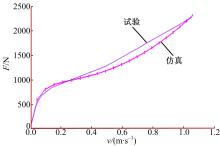
图7为减振器复原阀系的速度特性和示功图特性。从图7可以看出仿真结果与试验结果吻合较好, 速度分段特性表现明显。由于仿真周期为1/4正弦波, 所以对示功图只进行1/4部分拟合, 在速度特性曲线中, 两者在开阀前基本保持相同, 而在开阀后试验结果更趋于线性化, 仿真结果为曲线, 这是因为复原阀系中没有加入调整垫圈的缘故, 而且在示功图的高阻尼力状态也有以上情况出现。

图7 减振器复原阀系的速度特性和示功图特性(a)速度特性Fig.7 Velocity and indicator diagram characteristics of rebound valve

图7 减振器复原阀系的速度特性和示功图特性(b)示功图Fig.7 Velocity and indicator diagram characteristics of rebound valve

5.2 复原阀片非线性动态响应特性

叠加节流阀片的位移决定某一时刻油液流量和减振器阻尼大小。图8为阀片最大位移点的位移-时间历程和速度-时间历程, 减振器的三段特性在图中表现明显。减振器工作初始时间位移与速度值为零, 此时刻是复原阀系在低速工作状态下; 随着时间的推移, 位移与速度值有跳跃变化, 为减振器开阀点; 随着压力的增大, 节流阀片位移增大, 减振器工作进入第三段特性。从图8可以看出, 位移与速度跳跃变化发生在同一时刻, 证明仿真结果可靠。

图8 复原阀片位移-时间历程和速度-时间历程(a)位移-时间历程Fig.8 Displacement-time and velocity-time histories of rebound valve

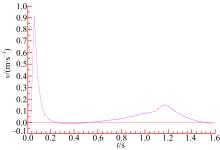图8 复原阀片位移-时间历程和速度-时间历程(b)速度-时间历程Fig.8 Displacement-time and velocity-time histories of rebound valve

图9 复原阀开阀前流场压力场Fig.9 Flow field pressure field before rebound valve is open

图10 复原阀开阀后流场压力场Fig.10 Flow field pressure field after rebound valve is open

5.3 减振器流场特性

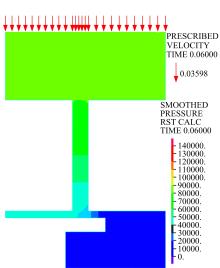
图9、图10分别为t=0.06 s、v=0.036 m/s, t=0.36 s、v=0.211 m/s的开阀前、后液体节流通道压力场, 从图中可以看出, 减振器在低速工作状态下, 节流通道内压力分布均匀, 油液流动状态为层流, 节流阀片所受压力较小, 节流阀片没有开启; 节流阀片在开阀后压力梯度变化明显, 此时油液运动状态为湍流, 节流阀片所受压力增大, 达到开阀点状态。

由图11可知, 阻尼通道的流量不断增大, 工作缸内的压差也在不断增大, 试验中, 减振器活塞杆运动速度越快, 阻尼力值越大。从图11可以看出, 压差与流量成线性变化, 与实际工作状态相符。

图11 复原阀p-Q特性Fig.11 Rebound valve p-Q characteristics

6 结束语

利用流-固耦合仿真方法得到车辆减振器非线性特性, 仿真结果与实际一致, 表明本文方法能够解决复杂的流-固耦合问题。阻尼通道和阀片的有限元模型对仿真精度影响最大。建立了与物理模型相近的流-固耦合有限元模型, 求解中考虑了阀片间的接触、阀片与活塞面的接触、多槽的流

动以及大位移变形。应用流-固耦合仿真方法可得到减振器的速度特性和示功特性, 对研究减振器阀系运动机理有重大意义。

The authors have declared that no competing interests exist.

参考文献
[1] 周长城, 顾亮. 筒式减振器叠加节流阀片开度特性试验[J]. 机械工程学报, 2007, 43(6): 210-215.
Zhou Chang-cheng, Gu Liang. Superposition throttle-slices opening size and characteristic test of telescope-damper[J]. Chinese Journal of Mechanical Engineering, 2007, 43(6): 210-215. [本文引用:1] [JCR: 0.263] [CJCR: 0.6991]
[2] 黄恒, 程广伟, 邓楚南. 车用减振器的外特性建模与仿真[J]. 汽车技术, 2005, 24(11): 19-22.
Huang Heng, Cheng Guang-wei, Deng Chu-nan. Modeling and simulation of external characteristic of automotive shock absorbers[J]. Automobile Technology, 2005, 24(11): 19-22. [本文引用:1]
[3] 檀润华, 陈鹰, 赵凡, 等. 汽车减震器新型数学模型的研究[J]. 汽车工程, 1998, 20(2): 113-117.
Tan Run-hua, Chen Ying, Zhao Fan, et al. A new mathematical model for shock absorbers in motor vehicles[J]. Automotive Engineering, 1998, 20(2): 113-117. [本文引用:1] [CJCR: 0.618]
[4] Duym S W R. Simulation tools, modelling and dentification, for an auto-motive shock absorber in the context of vehicle dynamics[J]. Vehince System Dynamics, 2000, 33: 261-285. [本文引用:1]
[5] Lang H H. A study of the characteristics of automotive hydraulic dampers at high stroking frequencies[D]. USA: University of Michigan, 1997. [本文引用:1]
[6] Duym S, Stiens R, Reybrouck K. Evaluation of shock absorber models[J]. Vehicle System Dynamics, 1997, 27: 109-127. [本文引用:1] [JCR: 0.766]
[7] Bathe K J. ADINA theory and modeling guide report ARD01-9[R]. New York: ADINA Co. Ltd. , 2001: 235-262. [本文引用:1]
[8] 姜海晨, 张娜, 于振环. 减振器叠加节流阀片非线性特性仿真分析[J]. 计算机仿真, 2012, 29(5): 338-342.
Jiang Hai-chen, Zhang Na, Yu Zhen-huan. Nonlinear characteristics simulation analysis of shock absorber throttle valves[J]. Computer Simulation, 2012, 29(5): 338-342. [本文引用:1] [CJCR: 0.5628]
[9] Bathe K J. ADINA-F theory and modeling guide: ARD08-9[R]. New York: ADINA Co. Ltd. , 2008: 26-28, 230-262. [本文引用:1]