作者简介: 李建桥(1953),男,教授,博士生导师.研究方向:车辆地面力学.E-mail:jqli@jlu.edu.cn
针对月面低重力环境,采用轮上载荷为20~60 N的轻载荷条件,以车轮轮上载荷和速度为试验因素,车轮沉陷为试验指标设计正交试验方案,在模拟月壤3种不同状态下进行筛网轮土槽试验,采集车轮实际沉陷值,并利用激光轮辙形貌测量装置扫描轮辙,采集表观沉陷值。通过回归分析,拟合得到模拟月壤不同状态下筛网轮沉陷关于轮上载荷和速度的二元线性回归方程,方程拟合较好,置信度均为0.99,且相关系数均在0.9以上。对比车轮实际测量沉陷值和回归方程计算沉陷值,二者相对误差范围为0.34%~8.24%。轮辙的表观沉陷与相应的实际沉陷变化趋势一致,且二者沉陷差值随轮上载荷增加呈现线性增加规律,本文结果可为通过轮辙表观沉陷预测车轮实际沉陷提供依据。
Experiments were performed to investigate the sinkage of wire mesh wheel under light load (in the range of 20 N to 60 N), which mimic the low gravity environment on lunar surface. The wheel load and wheel speed are taken as the experimental factors, the wheel sinkage is taken as the experimental index, and orthogonal experiment design method is adopted. The experiments were carried out on a single-wheel test bed for the wire wheels under three simulant regolith conditions. The actual wheel sinkages were collected, and the apparent sinkages were measured using a rut morphology laser scanning device. Using regression analysis, three linear regression equations were worked out with confidence degree of 0.99 and square correlation coefficients all above 0.9. The relative error between the actual wheel sinkage and the calculated sinkage by the regression equations ranged from 0.34% to 8.24%. The variation trend of the laser scanned apparent sinkage was in consistent with the actual sinkage. The linear relationship between the sinkage and the wheel load was obvious. This study verified that the actual sinkage can be predicted from the apparent sinkage.
车辆在松软地面上行驶时, 会引起土壤扰动, 尤其是较深的沉陷会造成行驶阻力增大, 使车辆难以或无法通过, 车辆的通过性不仅取决于自身的动力性, 更取决于车轮与土壤相互作用的力学特性[1, 2]。由于月球重力加速度约为地球的1/6, 其表面覆盖着一层厚厚的粉末状月壤, 导致月球探测车辆移动过程中容易出现沉陷、打滑, 甚至无法通过, 因此, 研究车轮与松软地面相互作用机理具有重要意义[3]。为提高和保障月球车在月面的通过性能, 可通过地面土槽试验, 研究车轮在松软地面的滑转和沉陷规律[4, 5]。目前国内大多数月球车原理样机车轮结构借鉴了前苏联的Lunokhod月球车和美国的LRV月球车的弹性筛网车轮, 例如, 中国空间技术研究院和哈尔滨工业大学以及上海航天技术研究院和上海交通大学研制的多款月球车原理性样机车轮均采用了筛网轮[6, 7]。筛网轮的网状轮缘结构, 可以避免尘土的堆积存留, 具有结构轻便和转向阻力小等优点, 但国内外关于筛网轮在松软地面沉陷方面的研究还比较少。另外, 限于设备条件, 大多数的月球车单轮土槽研究是以地球重力加速度下的轮上载荷为试验条件, 且贝克沉陷模型不适合车轮轮上载荷小于45 N条件下的车轮沉陷预测[8, 9]。因此, 针对月面重力环境, 在轮上载荷小于80 N的轻载荷[10, 11]条件下, 研究月球车车轮与土壤相互作用时的沉陷规律, 在预测车轮沉陷, 提高月球车能源利用效率, 保障月球车工作的可靠性方面具有重要意义。
针对上述情况, 本文研制出轻型土槽试验装置, 以车轮沉陷量为试验指标, 轮上载荷和车轮速度为试验因素进行单轮土槽试验。使用位移传感器采集实时车轮沉陷值, 并通过激光轮辙形貌测量装置对轮辙进行非接触扫描测量, 提取轮辙表观沉陷值, 通过对试验结果的分析, 研究试验因数对车轮沉陷的影响规律, 以及土槽车轮实际沉陷和表观沉陷的对应关系, 以期为预测深空探测车辆在松软地面的通过性提供重要参考。
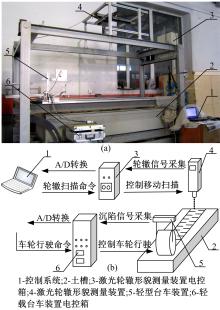
为了研究轻载荷条件下车轮沉陷规律, 吉林大学工程仿生教育部重点实验室研制出了轻型月壤-车轮土槽试验系统, 如图1所示, 主要由控制系统、土槽、轻型台车装置和激光轮辙形貌测量装置以及其对应的电控箱组成, 轻型月壤-车轮土槽试验系统的主要技术参数如下:土槽总体尺寸为1500 mm× 800 mm× 400 mm(长× 宽× 高); 最大被试轮直径为400 mm; 最大被试轮转速为20 r/min; 最大轮上法向载荷为100 N; 车轮沉陷测量范围为0~150 mm; 最大轮辙扫描面积为650 mm× 400 mm(长× 宽)。
轻型台车装置如图2所示。车架整体为杠杆结构, 通过改变后方配重砝码质量和位置可实现轮上法向载荷的无级调控; 水平位移传感器主要由D38H-8G05L-360BM-5M型滚轮编码器组成, 其有效水平位移测量范围为0~5 m, 测量精度为0.01 mm; 垂直位移传感器为拉线式位移传感器, 用于测量车轮行驶过程中的实际沉陷值, 其型号为XPS-S-5000-11R0, 测量行程范围为0~5000 mm, 测量精度为0.01 mm。
激光轮辙形貌测量装置固定于土槽顶部, 硬件主要由激光测距仪、二维移动框架和驱动步进电机组成, 其中激光测距仪型号为DLS-C15, 测距范围为0.05~65 m, 测距分辨率达到0.1 mm, 水平方向最大线扫描长度为0.65 m[12]。
本文采用吉林大学工程仿生实验室研制的JLU-2a型模拟月壤为试验介质, 主要以火山灰为原料加工配制而成, 其粒径分布和物理力学性质均在真实月壤样本的变化范围之内[13]。
被试车轮为鼓形弹性筛网轮, 轮径为300 mm, 轮宽为150 mm, 轮刺高10 mm, 如图3所示。筛网轮轮缘由3个轮圈构成, 中间轮圈直径大于两侧轮圈直径, 两排轮刺交错且等间距地安置于相邻轮圈上, 轮面筛网由直径为0.6 mm的钛合金编织而成。
本试验中使用的轻型台车装置采用了杠杆结构, 考虑到车轮在行驶过程中, 车轮沉陷和轮刺的存在使得轮心在水平方向上有一定的角度波动, 可能会对轮上法向载荷产生影响, 因此, 试验前对车轮轮上法向载荷进行标定。通过改变台车后方车架上加载的砝码质量及其相对车架的位置, 使电子天平显示出所需要的轮上载荷数值(精度为0.01 N), 同时记录对应的传感器显示数值, 通过拟合得到轮上载荷的标定线和方程, 如图4所示。结果显示拟合方程的线性度较高, 沉陷和轮刺导致法向轮上载荷的波动较小, 满足试验需要。
试验前, 通过激光轮辙形貌测量装置对整备后的模拟月壤基准平面进行线扫描, 扫描间距为5 mm, 扫描长度为250 mm; 试验中考虑到土槽有效试验区域范围和驱动电机稳定工作段, 土槽台车行驶的水平总位移选为1000 mm, 取位移范围为200~800 mm所采集的数据为车轮实际沉陷有效段数值; 试验后对轮辙沿车轮行进方向进行第二次线扫描, 扫描间距为1 mm, 扫描长度为250 mm, 两次扫描对应数据差值的均值即为轮辙表观沉陷值, 如图5所示。
(1)轮上法向载荷。月面环境下月球车车轮载荷小于100 N, 例如质量为140 kg的六轮月球车, 在水平月面上的平均车轮法向载荷约为40 N。考虑到月球车处于不同位姿时轮上载荷会有相应波动, 轮上法向载荷范围取为20~60 N。
(2)车轮行驶速度。月球车在执行月面巡视任务时, 需要根据月面传回的拍摄图片对就位地形进行分析和判断, 从而调整月球车位姿以及进行合理的路径规划, 因此月球车行驶速度一般较低, 本试验中车轮行驶速度范围取为10~100 m/h。
(3)模拟月壤状态。模拟月壤在不同紧实度下呈现的物理力学特性会对试验产生不同的结果[12], 结合试验需要以及整备方法稳定性和效率的基础上, 选择3种整备方法, 使得模拟月壤达到3种不同状态:松软状态、自然状态和紧实状态, 通过土壤硬度计检测整备效果, 3种不同状态模拟月壤对应的贯入阻力最大值分别为600、900、1500 kPa, 均在真实月壤硬度范围内。
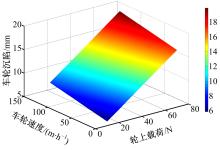
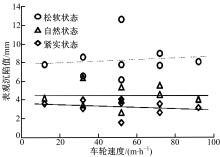
模拟月壤不同状态下, 车轮沉陷规律如图6所示。由于被试轮的轮面为弹性筛网结构以及轮刺的存在, 行驶过程中轮上法向动载荷值大于其静态标定轮下载荷值。3种模拟月壤状态下, 筛网轮沉陷范围分别为:10.6~19.3 mm(松软状态)、9.2~14.4 mm(自然状态)、6.3~10.3 mm(紧实状态)。由于模拟月壤在松软状态下很容易从车轮筛网胎面的空隙中漏出(见图7), 且随着轮上载荷的增大漏土现象越明显, 因此松软状态下车轮沉陷增大的趋势最为明显。当轮上载荷小于40 N, 自然状态与松软状态下车轮沉陷量接近, 原因是由于自然状态下轮上载荷较小时, 车轮与模拟月壤表层接触面较小, 车轮在行驶时出现一定滑转, 滑转沉陷使得总体车轮沉陷偏大。
| 表3 车轮沉陷拟合方程 Table 3 Fitted equations of wheel sinkage |
分析方程发现, 车轮沉陷随轮上载荷和车轮速度呈线性变化规律, 且轮上载荷对车轮沉陷的影响较车轮速度的影响大。试验条件下, 车轮沉陷随载荷增加相对变化率分别为82.1%(松软状态)、56.5%(自然状态)和63.5%(紧实状态); 车轮沉陷随车轮速度增大的变化率则较小, 对应沉陷变化率分别为6.5%(松软状态)、8.0%(自然状态)和3.8%(紧实状态)。另外, 随着模拟月壤由松软状态变至紧实状态时, 车轮速度对车轮沉陷的影响越来越小, 分析是由于随着模拟月壤的密实度增加, 车轮轮刺进入模拟月壤的速度对其扰动作用越来越不明显。
对车轮沉陷实测值与回归方程计算值进行比较发现, 随着模拟月壤由松软状态变至紧实状态, 二者残差以及相对误差均总体呈现逐渐减小趋势, 如表4所示, 其中, 残差最大值不超过1.4 mm, 二者的相对误差范围为0.34%~8.24%, 且相对误差均值不超过3.97%, 因此, 回归方程能为车轮沉陷预测提供较好的参考依据。
| 表4 车轮沉陷实测值与计算值比较分析 Table 4 Comparative analysis between measured wheel sinkage and calculated wheel sinkage |
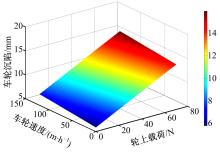
模拟月壤3种状态下, 轮辙表观沉陷随着轮上载荷和车轮速度的变化, 如图9所示。对比车轮实际沉陷和轮辙表观沉陷发现, 二者的变化趋势保持一致。由于被试车轮胎面为筛网结构, 行驶过程中部分模拟月壤从胎面网格空隙中漏至筛网轮胎面内侧, 并回填至轮辙表面, 由于扫描提取的表观沉陷值为车轮行走后轮辙表面与基准面差值, 而车轮实际沉陷为基准面与筛网面最低点的高度差, 因此提取的轮辙表观沉陷值将始终小于车轮的实际沉陷值。另外, 由于车轮行走后模拟月壤的部分回弹也会使得提取的表观沉陷值有所减小。
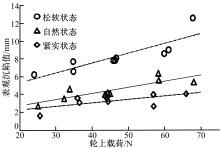
不同模拟月壤状态下, 车轮实际沉陷和表观沉陷的差值变化规律如图10所示, 其范围分别为:4.2~7.4 mm(松软状态)、6.5~8.8 mm(自然状态)、3.8~6.2 mm(紧实状态)。
 | 图10 模拟月壤不同状态下的车轮实际沉陷与表观沉陷差值变化规律(a)不同轮上载荷Fig.10 Difference between wheel sinkage and apparent sinkage under different soil conditions |
 | 图10 模拟月壤不同状态下的车轮实际沉陷与表观沉陷差值变化规律(b)不同车轮速度Fig.10 Difference between wheel sinkage and apparent sinkage under different soil conditions |
分析车轮沉陷和表观沉陷的差值发现, 自然状态下沉陷差值较松软状态的大, 原因可能是由于松软状态下模拟月壤较为松散, 车轮在行驶过程中筛网胎面和轮刺很容易将一部分模拟月壤粘附带走并送至车轮前方, 导致表观沉陷值增大, 车轮沉陷和表观沉陷的差值则相应减小。紧实状态下沉陷差值总体较小, 这是由于紧实状态下的车轮沉陷较小, 筛网胎面的漏土现象较弱, 从而使得车轮沉陷和表观沉陷接近, 二者沉陷差值较小。
当轮上载荷小于40 N时, 松软状态与紧实状态下的沉陷差值接近, 原因可能是轮上载荷较小时, 车轮行驶过程中轮刺挑土现象明显, 轮辙中由轮刺产生的V型坑较深, 导致表观沉陷偏大, 随着载荷的继续增大, 筛网轮实际沉陷增加, 胎面漏土的影响逐渐大于轮刺挑土现象的影响, 此时松软状态下的沉陷差值逐渐大于紧实状态下的对应差值。
(1)轮上载荷和车轮速度范围分别为20~60 N和12~92 m/h时, 模拟月壤不同状态下筛网轮的沉陷范围分别为10.6~19.3 mm(松软状态)、9.2~14.4 mm(自然状态)、6.3~10.3 mm(紧实状态), 其中, 松软状态下车轮沉陷变化范围较大。
(2)轮上载荷对车轮沉陷的影响较车轮速度的影响大, 车轮沉陷随轮上载荷增大而增大, 模拟月壤在3种状态下车轮沉陷相对增大率分别为82.1%(松软状态)、56.5%(自然状态)和63.5%(紧实状态)。试验条件下, 车轮沉陷随车轮速度增大而产生的变化率较小, 分别为6.5%(松软状态)、8.0%(自然状态)和3.8%(紧实状态)。
(3)模拟月壤不同状态下, 来自轮辙的表观沉陷与车轮实际沉陷的差值范围分别为:4.2~7.4 mm(松软状态)、6.5~8.8 mm(自然状态)、3.8~6.2 mm(紧实状态)。车轮实际沉陷与表观沉陷差值在自然状态下最大, 紧实状态下最小。随着轮上载荷变化, 轮辙表观沉陷与车轮实际沉陷变化趋势保持一致, 二者沉陷差值随着轮上载荷增大呈现线性增大规律, 上述研究结论为通过轮辙判断车轮实际沉陷提供了依据。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|