针对湿式离合器接合过程中的局部高温区及影响因素,利用热弹性不稳定性理论(TEI)进行了理论建模与分析。模型中考虑了材料表面粗糙度和混合润滑对摩擦副温度和压力的影响,分析了混合润滑状态下润滑区域与接触区域的比例以及油膜剪切热量与摩擦热量的比例。为了准确测量材料表面粗糙度,设计台架试验,利用表面形貌仪测试了对偶片表面形貌,分析了粗糙度在离合器不同使用阶段的变化规律。结果表明,当离合器接合转速超过临界值时,温度场分布出现明显的波动,高、低温区间隔分布。同时,指出了离合器摩擦材料参数(导热性、弹性)与结构参数(对偶片厚度)对稳定性的影响。
On the basis of Thermoelastic Instability (TEI) theory, a theoretical model is proposed to investigate the local hot zones and influence factors of wet clutches during engaging process. The effects of the surface roughness and the mixed lubrication on the temperature and pressure of the friction pair are considered. Under mixed lubrication, the ratios of the lubrication area to the contact area and the fluid shear velocity induced heat flux to the frictional heat flux are calculated. A plasmon resonance analyzer is used to investigate the variation of the surface roughness in different stages. The results show that strong inhomogenous temperature field, hot zones and cold zones appear when the clutch engaging speed exceeds the threshold. The material properties, such as thermal conductivity and elasticity, and structural properties, such as the thickness of the matting disk, significantly influence the stability of the system.
由于离合器接合过程中主从动部分相对速度一般较大, 接合时间一般较短, 所以摩擦产生的大量热量来不及向外界扩散, 基本被离合器摩擦副吸收, 摩擦副温升较高。为了保证离合器可靠工作, 在其设计过程中必需保证一次接合温升小于摩擦副的许用温度。传统离合器设计中, 滑摩功、一次接合温升和平均温升等参数均为重要参数, 学者对其进行了一系列研究。高晓敏等[1]研究发现, “ 摩擦面许用瞬时温度” 可以直接、准确地反映摩擦片及对偶片的热负荷情况。林腾蛟等[2]建立了湿式离合器摩擦副的三维热传导分析模型, 并给出了湿式摩擦离合器的摩擦热和对流换热系数计算公式。
仅通过计算滑摩功与平均温升无法全面反映离合器摩擦副的温度场分布情况。由于离合器在安装时存在误差、摩擦副表面可能存在缺陷以及摩擦材料的各向异性等原因, 摩擦副温度场一般呈现非均匀分布, 可能存在局部高温区。引起局部高温区的主要原因之一是摩擦副的热弹性失稳。离合器在接合过程中, 常由于摩擦副表面温度过高, 造成表面损伤从而影响其性能和寿命。早期研究多以滑摩功为评价标准, 基于摩擦热均匀分布的假设, 计算离合器接合过程中的功率损失以确定温升情况。随着有限元理论与仿真技术的发展, 研究重点转向利用仿真软件分析热弹耦合或热机耦合对温度场分布的影响, 得到了温度场存在非均匀分布、局部高温区等结论[3, 4]。局部高温区有多种形式, Anderson等[5]将其分为四种类型:粗糙型, 焦点型, 畸变型和区域型。粗糙型由瞬间高温引起, 不会留下可见痕迹, 其成因是接触表面的粗糙度。系统处于稳定状态时, 只产生粗糙型高温区。焦点型是由热弹性不稳定(Thermoelastic instability, 简称TEI)引起, 摩擦表面有可见灼烧痕迹, 此类高温区只有在离合器工作转速超过临界转速时才会出现, 常沿圆周方向分布, 也被称为热点(Hot spots)。畸变型是由材料热变形引起, 摩擦面存在点状或带状痕迹。区域型由接触压力、钢片厚度、摩擦因数的非均匀性或散热不良等因素引起。
TEI理论是研究摩擦元件稳定性以及温度场非均匀分布的热弹性理论, 由Barber提出[6]。当离合器接合速度大于临界速度时, 系统失去稳定性, 接触压力以及温度场出现强烈非均匀性, 并随时间呈指数增长, 最终形成局部高温区[7]。Hartsock等[8]通过理论建模的方法研究了多片式制动器的TEI与临界速度问题; Yi等[9]采用有限元法求解TEI扰动增长系数以及温度场分布取得了成功。湿式离合器在接合过程中, 发热机理与制动器等干式摩擦元件不同, 研究过程需要考虑油膜剪切生热与油膜厚度对稳定性的影响。Zhao等[10]首先通过理论建模研究了端面油封的TEI问题; Jang与Khonsari[11]在Banergee模型的基础上考虑了表面粗糙度的影响, 求解系统的临界速度, 发现粗糙度对系统的稳定性具有重要影响。
本文将采用台架试验测试湿式换挡离合器的表面粗糙度, 研究离合器在不同使用阶段粗糙度的变化情况以及其对系统稳定性的影响, 并通过理论建模的方法, 研究系统临界速度的变化情况。另外, 还研究了离合器材料参数和结构参数对其稳定性的影响, 为提高离合器性能和寿命, 改进离合器设计提供参考和依据。
试验中多次接合湿式换挡离合器, 经不同次数的接合后用NanoMap-D轮廓仪对离合器对偶钢片进行表面形貌的测试与分析。在离合器接合100、300、500、800、1000、1200、1500和1800次时, 拆箱检测离合器钢片表面粗糙度。
试验研究对象为某液力机械综合传动装置中的多片式湿式换挡离合器, 其摩擦片由金属芯片和铜基粉末冶金材料烧结而成, 金属芯片和对偶钢片均采用65Mn钢材料, 对偶钢片厚度为2 mm, 材料参数如表1所示。
| 表1 离合器材料参数 Table 1 Material properties of clutch |
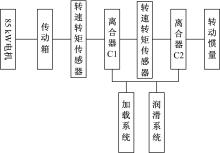
台架试验布置如图1所示, 其中研究对象为离合器C1。动力系统采用Siemens公司的85 kW变频调速电机, 电机输出动力通过传动箱到达离合器C1, 利用转速转矩传感器测量C1的输入与输出转速、转矩, 动力最后经离合器C2传递至转动惯量, 通过转动惯量模拟离合器接合过程中的动力输入。当转动惯量达到预定转速后分离离合器C2与C1, 并停止电机; 电机停止后, 接合离合器C2, 最后使离合器C1的钢片和摩擦片逐渐接合并同步。
试验中润滑油黏度为0.098 Pa· s, 内部压力为0.4 MPa, 对偶材料粗糙峰密度 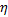

| 表2 对偶钢片粗糙度变化情况 Table 2 Changes of surface roughness of mating plate |
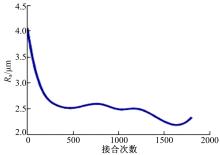
由图2可知, 磨合阶段对偶钢片表面粗糙度较大, 大约为4 μ m, 在接合大约400次后迅速下降到2.5 μ m, 在后续接合过程中粗糙度变化较小。在后续理论分析中将以试验数据为依据, 研究离合器不同使用阶段稳定性的变化情况。
离合器一次接合温升由稳态温升和扰动温升组成, 其中稳态温升表示摩擦副的平均温升, 可以由一次接合的滑摩功推导得到; 扰动温升指由系统内初始非均匀性因素引起的温升, 可以通过TEI分析与热弹性力学分析得到。
首先计算稳态温升, 滑摩功是指由于离合器主从动部分间存在相对滑动, 接合过程中消耗的功。滑摩功可以由接合过程中主从动部分输出功的差值计算[12]:
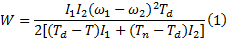
式中:I1 、I2 分别表示离合器主、从动部分的转动惯量; ω 1 、ω 2分别表示主、从动部分的角速度; Td 、T、Tn 分别表示离合器的动摩擦转矩、额定转矩和输入转矩。@实验中离合器输入端转速基本保持不变, 所以(Tn-Td)=0, )I1 、I2 分别表示离合器主、从动部分的转动惯量; ω _1 、ω _2 分别表示主、从动部分的角速度; Td 、T、Tn 分别表示离合器的动摩擦转矩、额定转矩和输入转矩。@实验中离合器输入端转速基本保持不变, 所以(Tn-Td)=0, )式(1)可以简化为:
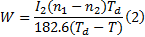
式中: n1 、n2 分别表示离合器主、从动端转速。@采用输出端制动等效模拟离合器接合过程的方法, 所以从动端转速n2=0, I2→ ∞ , )式(2)可以简化为:
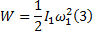
由于离合器一次接合时间很短, 摩擦热在短时间内来不及向周围介质扩散, 基本被摩擦副全部吸收, 一次接合温升可以表示为:
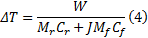
式中:Mr 、Mf 分别为离合器对偶片和摩擦片的质量; Cr 、Cf 分别为对偶片和摩擦片的比热; J是摩擦材料的吸热系数, 对于粉末冶金材料, J=1。
摩擦材料包括有机材料和无机材料, 有机材料包括编制类、模压类和纸基材料; 无机材料包括金属陶瓷材料、粉末冶金材料、碳/碳复合材料[12]。对偶材料一般采用合金钢或者碳素钢, 由于大多数摩擦材料的导热性远小于对偶材料, 所以在离合器接合过程中大部分摩擦热传导进入对偶片, 只有少量摩擦热传导进入摩擦片。为简化建模过程, 将摩擦片简化为静止的半无限大热绝缘体, 对偶片简化为运动的半无限大热导体[9]。TEI问题的研究重点是摩擦元件圆周方向的非均匀温度场, 所以建立二维模型, 可以获得较准确的分析结果。
TEI问题的研究方法是扰动研究法, 即将物理场表示为一个稳态量和一个正弦或者余弦扰动的叠加, 以表示物理场的非均匀性。对于物理场中的真实扰动, 可以通过傅立叶变换表示为余弦扰动的叠加。通过研究余弦扰动幅值的变化情况, 即可求解系统发生TEI的临界速度。由于此方法物理意义明确, 并可以简化分析过程, 所以在TEI分析中广泛应用。理论模型中坐标系 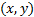
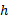
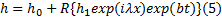
式中: R表示取实部; h0 、h1 、b、λ 分别表示油膜厚度稳态值、油膜厚度扰动值、扰动增长系数和扰动空间频率; i表示虚数单位。
通过计算扰动增长系数, 即可确定系统的稳定性。如果扰动增长系数 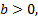
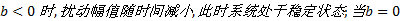
考虑摩擦副表面粗糙度对于油膜厚度的影响, 稳态油膜厚度h0 可以表示为平均油膜厚度ha 与粗糙度Ra 的叠加。假设摩擦副粗糙度分布符合高斯分布, 则h0可以表示为[11]:
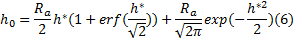
式中:无量纲单位 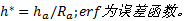
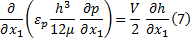
式中:V、p、μ 分别代表摩擦副相对速度、润滑油压力和黏度; ε p表示流体压力因数:
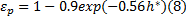
根据扰动法, 润滑油压力可以表示为:
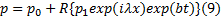
将方程(5)(9)代入方程(7), 求解偏微分方程可得
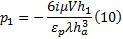
根据纳维-斯托克斯方程有:
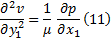
边界条件为 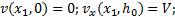
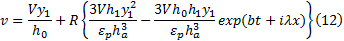
根据牛顿内摩擦定律, 由油膜剪切力产生的热流密度扰动为:
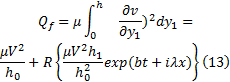
在考虑表面粗糙度的条件下, 离合器接合时, 其表面部分处于流体润滑状态, 部分处于直接接触状态。单位面积上的直接接触区域比例 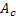
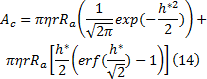
当摩擦副处于混合润滑状态时, 摩擦热由油膜剪切热量与干摩擦热量组成, 所以, 总热流密度 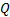
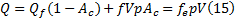
式中:f表示摩擦副接触处的摩擦因数; fe代表等效摩擦因数。将式(13)代入式(15), 可以求解等效摩擦因数的稳态值表达式为:
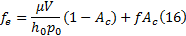
离合器摩擦片与对偶片的温度场分布均满足固体瞬态热传导方程:
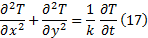
式中: 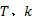
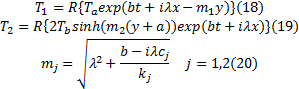
根据摩擦副接触处温度相等, 可以求解温度场表达式中的常数 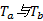
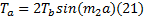
根据热流密度与温度场的关系, 摩擦副接触处能量平衡方程为:
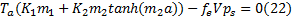
式中: 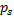
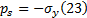
通过热弹性力学分析, 可以求解固体正应力表达式, 代入方程(22)(23), 可以求得能量平衡方程。由于此方程是复数方程, 所以方程成立的充分必要条件是其实部与虚部同时为零, 将速度关系 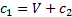
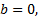
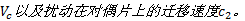
根据表1和表2所示的离合器参数, 假设离合器接合速度是10 m/s, 首先计算不同粗糙度下的单位面积上的直接接触区域比例Ac。由于本文主要针对混合润滑状态下系统的TEI问题, 所以假设初始油膜厚度等于初始粗糙度, 取4 μ m, 计算结果如表3所示。由表3可知, 当离合器处于磨合阶段, 即接合次数在0~100次时, 直接接触面积比例为2.75%~3.52%; 当离合器进入正常使用阶段, 即接合次数大于300次时, 直接接触面积比例基本稳定在2.2%左右。
| 表3 不同接合次数下的接触面积变化 Table 3 Changes of contact surface area for different engagements |
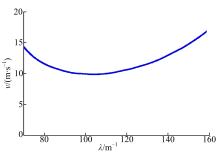
由于离合器在正常使用阶段表面粗糙度与直接接触面积比例变化较小, 所以后续研究中采用离合器接合300次时的粗糙度, 计算等效摩擦因数以及系统发生TEI时的临界速度, 扰动空间频率与临界速度关系曲线如图3所示。
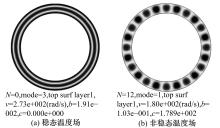
λ 与离合器对偶钢片与摩擦片的热点数N的关系为N=λ R。其中, R扰动空间频率表示离合器等效半径。图3可以用于判断离合器是否处于TEI状态, 当离合器接合转速小于临界速度时, 系统处于稳定状态; 当其大于临界速度, 系统进入TEI状态, 如果接合时间足够长, 摩擦副表面将出现局部热点。不同模态扰动对应不同热点数和临界速度, 例如当离合器接合速度为10 m/s时, 系统可能出现10~12个热点。通过仿真分析, 当接合速度小于临界速度时, 对偶片表面温度场分布如图4(a)所示; 当其超过临界速度时(10 m/s), 温度场分布如图4(b)所示。图4中深色的区域表示高温区, 浅色的区域表示低温区。
由图4可知, 当系统处于稳定状态时, 温度场沿圆周方向均匀分布, 同时由于离合器摩擦副内外径处滑摩线速度不同, 温度场沿半径方向呈现非均匀分布; 当系统处于TEI状态时, 由于接触压力扰动随时间不断增长, 导致温度场在圆周方向也出现非均匀分布, 形成局部高温区, 即热点。在滑摩功不变的条件下, 热点的出现可以导致局部温度超过材料许用极限, 或者由于表面温差过大而导致局部热应力超过材料极限而失效。临界速度与系统的结构以及材料参数有关, 提高临界速度可以增强系统热弹性稳定性。
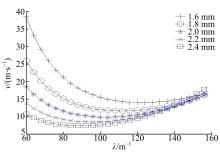
离合器对偶钢片厚度是影响系统临界速度的重要因素之一, 离合器设计中对于外径小于250 mm的对偶钢片, 其厚度一般取0.8~2.4 mm[12]。保持其他系统结构和材料参数不变, 将对偶钢片厚度分别取1.6、1.8、2.0、2.2、2.4 mm, 系统临界速度如图5所示。由图5可知, 对偶钢片厚度越小, 最小临界速度越大, 说明系统稳定性越高。产生这种现象的原因是:当对偶钢片厚度减小时, 其热弹性变形相对增大, 热弹性应力扰动相对减小, 有利于增加系统稳定性。然而, 对偶钢片厚度减小会引起系统热容量的减小, 在相同滑摩功时会增大系统的稳态温升。在离合器设计中, 应当首先校核系统稳定性, 在保证稳定性的前提下尽量增大对偶钢片厚度。
粉末冶金材料热稳定性高、热传导性好、高温下强度高且耐磨损, 被广泛应用于湿式离合器摩擦材料[12]。改变原料比例, 可以改变粉末冶金材料的性能参数, 例如弹性模量、导热系数等。
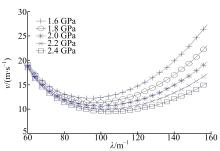
弹性模量越大, 在一定应力的作用下, 材料的弹性变形越小。为研究弹性模量对稳定性的影响, 在保持结构参数和其他材料参数不变的前提下, 摩擦衬片的弹性模量分别取1.6、1.8、2.0、2.2、2.4 GPa, 临界速度曲线如图6所示。由图6可知, 摩擦材料弹性模量越低, TEI临界速度越高, 说明系统稳定性越好。此现象的产生机理是:在滑摩过程中, 相同的弹性变形下, 弹性模量大的摩擦材料容易在接触表面出现较大的接触应力。在接触压力扰动相同的条件下, 弹性模量大的材料其热弹性应力扰动更大, 所以系统稳定性较差。
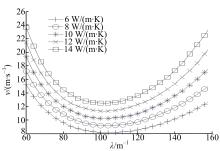
导热系数越大, 材料导热性越好。在保证离合器结构参数和其他材料参数不变的前提下, 摩擦材料导热系数分别选取6、8、10、12、14 W/(m· K), 临界速度曲线如图7所示。观察图7可以发现, 导热系数越大, 临界速度越高。其原因是滑摩过程中, 大部分摩擦热传导进入对偶钢片, 如果采用具有较高导热系数的摩擦材料, 将有更多摩擦热通过传导进入摩擦材料, 同时进入对偶钢片的摩擦热将减少, 即摩擦热在对偶钢片与摩擦片之间的分配更加平均, 系统均匀性提高, 临界速度提高, 稳定性增加。
(1)湿式离合器接合速度超过临界速度后, 温度场沿圆周方向出现局部高温区, 即热点。不同模态扰动引起不同热点数, 对应不同的临界速度。
(2)湿式离合器对偶钢片表面粗糙度影响摩擦副直接接触面积, 从而影响接合过程的发热量和系统热弹性稳定性。磨合阶段表面粗糙度变化较大。正常使用阶段粗糙度变化较小, 对临界速度的影响可以忽略。
(3)减小离合器对偶钢片厚度可以提高TEI临界速度, 从而提高系统的稳定性。同时, 减小对偶钢片厚度会降低系统热容量, 提高稳态温度, 设计时应当综合考虑。
(4)湿式离合器摩擦材料的导热性和弹性影响TEI临界速度。弹性模量越小, 导热系数越大, 临界速度越高, 系统稳定性越好。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|