对于故障诊断问题, 基于模型诊断是一种良好的解决方法, 得到了理论和应用双方研究人员的重视, 产生了一系列理论成果和应用系统, 如通讯网络诊断^[1]、飞行器诊断^[2]等。

早期的基于模型诊断方法针对的是静态系统, 但是对于大型的实际应用系统, 完全停机带来的损失较大, 这种限制使得基于模型诊断方法向动态发展, 产生了离散事件系统条件下的基于模型诊断方法, 该方法不需要系统停机即可以诊断, 在线进行推理, 得到诊断结果。并且, 离散事件系统的基于模型诊断得到的不仅是系统是否存在故障以及故障类型, 而且包含故障产生的过程, 诊断结果更加完整。

所有的基于模型诊断基于一个共同的前提, 那就是待诊断系统必须是可诊断的。即可诊断性应作为诊断问题的前提。但是, 随着系统行为越来越复杂, 可诊断性判定的效率也随之降低。针对离散事件系统的可诊断性判定效率的研究主要分为两类:针对方法的改进和针对模型的改进。

针对方法的改进主要通过模型上的不同操作来实现。文献[3, 4]首先提出了构建诊断器的方法, 并应用于一个工业系统上。这种方法通过生成带有故障标签的有限状态自动机, 在自动机上判断故障标签的一致性来得到系统的可诊断性, 其效率是状态的指数级。文献[5]在构建诊断器的方法上提出了改进, 建立双树模型, 通过模型自身的同步来得到可诊断性, 将可诊断性测试的效率降低到了状态的多项式级。在双树模型的基础上, 文献[6]提出了改进, 修改算法过程, 用记录轨迹事件集合的方法来判断可诊断性, 进一步提高了可诊断性的判定效率。而文献[7]提出了模式可诊断性, 忽略除故障外的全部事件, 仅关注故障, 通过预编译来提高效率, 并在分布式系统上进行改进^{[8, 9]}。

针对模型的改进主要通过降低模型规模, 分解模型至分布式或分散式系统, 在小规模的模型上进行可诊断性的判定, 通过并行和缩减可诊断性测试空间来提高可诊断性测试效率。文献[10]提出了在分散式模型中的可诊断性判定方法, 并指出了原有模型和分解模型组之间可诊断性的传递关系。在模型被分解为分布式或者分散式时, 原有的转移或因果信息可能被丢失, 文献[11]提出了同步方法, 用以解决分布式或分散式模型可诊断性不一致的问题。文献[12]提出了分布式模型中的强可诊断性及弱可诊断性概念, 定义了不同规模模型之间可诊断性之间的传递关系。文献[13]提出了同步的优化问题, 降低了同步通讯的成本。由于分布式模型上的可诊断性计算及诊断方法效率较高, 一些经典的可诊断性及诊断方法也被应用于分布式或分散式系统^{[14, 15]}。

本文在上述两类方法的基础上, 提出一种改进的增量可诊断性测试方法, 在将模型划分为由窗口决定的模型链之后, 根据增量观测判定系统的可诊断性。增量过程中, 待判定的模型将不断被剪枝, 可诊断性测试的空间也将不断缩小。同时, 由于增量方法仅考虑上一次的结果和本次的观测, 搜索的效率较高。

基于模型诊断的第一步是对系统建模, 将物理系统的行为映射到逻辑系统上, 得到能被诊断系统接受并处理的模型。离散事件系统是一种同时具有静态行为和动态行为的模型系统, 可以用自动机来表示。

定义1(模型) 模型被定义为一个五元组的自动机G=(Q, E, T, I, M), 其中Q是有限状态集合; E是有限事件集合, 包含空事件ε ; T是转移集合, T⊆Q× E× Q, 表示系统从一个状态经某事件触发转移到另外一个状态; I是初始状态集合, I∈ Q; M是标记状态集合, M⊆Q, 在离线过程中, M是终止状态集合, 在线过程中, M表示当前终止状态集合。

转移表示的是状态之间的直接可达关系, 若∃t∈ T, t=q× e× q', 则称q到q'直接可达, 记为q→ q', 扩展直接可达关系, 描述任意两个状态之间的可达关系, 即∃q, q', q₁, …, q_i∈ Q, 有如下关系q→ q₁, q₁→ q₂, …, q_i→ q', 则称q到q'可达, 记为q q'。若q∈ I, 则q q'被称为从q到q'的轨迹。

轨迹是状态与事件交替出现的序列, 实际表示的是事件不断驱动状态变化的过程。事件集合元素的有限长度序列集合记为E^* 。在轨迹中的事件序列描述了系统的行为过程, 能被模型接受的事件序列被称为语言, 是模型中任意一条轨迹上的事件序列, 全部语言的集合记为L(G), L(G)⊆E^* 。在完备离散事件系统中, ∀ l∈ L(G), pre(l)∈ L(G)。其中pre(l)表示l的前缀。L(G)是前缀关闭的, 这表示∀ l∈ L(G), l=st, s∈ L(G)。即, 任意语言的前缀也是语言。在完备模型中, 前缀关闭的性质保证了增量过程中可诊断性的确定性和连续性。

事件集合据其性质可以分为3个子集:可观测事件集合E_o, 正常事件E_n, 故障事件E_f, 其中E_o∩ E_n=⌀, E_o∩ E_f=⌀, E_f∩ E_n=⌀, E_o∪ E_n∪ E_f=E。

在系统外部, 仅能获得可观测事件, 根据可观测的事件序列推理得到在全部状态集合和事件集合上发生的全部可能行为, 并推理得到系统可诊断性。外部系统与内部行为一致, 通过一个函数将事件集合投影到可观测事件集合。

定义2(可观测投影) 可观测投影是事件集合向可观测事件集合上的投影:

可观测映射可以扩展到对语言的映射上:

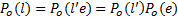
语言上的可观测映射将语言中的不可观测事件(正常事件, 故障事件)“ 抹去” , 仅留下可观测事件序列, 这与系统外部能探测到的信息是一致的。相似地, 事件集合也可以投影到故障事件集合上, 用于判断一个系统行为过程中是否存在故障。

定义3(故障投影) 故障投影是事件集合向故障事件集合上进行的投影:

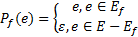
同样地, 定义在语言上的故障投影:P_f(l)=P_f(l'e)=P_f(l')P_f(e), 用于标记语言中存在的全部故障。

语言的可观测投影和故障投影均存在着逆向的投影:

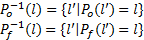
投影与逆向投影未必一一对应, 可能存在多个语言, 它们投影到可观测语言上的结果是相同的。若这些具有相同观测的语言中的故障不同时, 就意味着故障不能在外部被区分, 这对于系统是危险的, 对于诊断系统也是不可接受的。因此, 在建模之后, 诊断系统运行之前, 需要对系统的可诊断性进行测试。

定义4(故障可诊断^[3]) 若∀ l∈ L(G), |l|> n, l'∈ 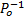(P_o(l))⇒ ∀ P_f(l')=f, n∈ N, 则称语言l关于故障f是故障可诊断的, 定义谓词D(l, f)=true, 否则D(l, f)=false。若∀ l∈ L(G), ∀ f∈ E_f, D(l, f)=true, 则称系统G是故障可诊断的, 记为D(G)=ture, 否则D(G)=false。

故障可诊断的判定中, 当可观测序列长度大于一定值时, 可诊断性才是确定的, 否则可诊断性可能不确定。这与观测长度有关, 而观测长度通常与时间有关。

定义5(时间轴) 定义时间轴是关于时间点的无限序列, X=< X₀, X₁, …, X_i, …> 。并且∀ x_i, x_j∈ X, x_i< x_j⇔ i< j。

在特定时间点x上的标记状态集合定义为M_x。

由于在不同时间点上, 标记状态和可诊断性不确定, 虚拟一个在线过程, 增量地延长观测长度, 逐步确定可诊断性。

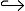
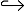
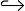
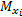
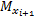
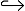
定义6(观测窗口) 观测窗口W_m=< o₁, o₂, …, o_n> , ∀ o_i, o_i+1∈ E_o, ∃q_m× o_i× q_n, q_s× o_i+1× q_t∈ T。q_m q_n q_s q_t, 其中n是窗口的规模, 表示一次增量所包含的可观测事件数量。增量过程中, 任意两个连续的时间点x_i、x_i+1, x_i上的标记状态集合 将被x_i+1上的状态集合 更新, 并且∀ q'∈ , ∃q∈ , (q q')∨ (q=q')。

由于标记集合随时间变化更新, 定义在任意时刻x上可以被接受的语言。

定义7(标记语言集合) 在x时刻, 当前标记状态集合M_x下, 标记语言集合为:L_x(G)={l|=< e₀, e₁, …, e_n> , q_i× e₀× q_j∈ T, q_i∈ I, q_m× e_n× q_t∈ T, q_t∈ M_x}∪ {l'|l'=pre(l)}。前缀pre(l)中包括空事件ε 。标记语言集合表示的是在时间点x上系统可以接受的全部语言。在标记语言上定义当前的可诊断性。

定义8(标记可诊断) 若在x时刻上, 终止于标记状态集合M_x的语言集合为L_x(G), ∀ l∈ L_x(G), ∀ f∈ E_f, D(l, f)=true, 则称在x时刻上, L_x(G)是标记可诊断的。

在窗口增量到来时, 在当前的标记状态集合上更新, 并根据窗口对当前语言进行区分:剪枝或扩展, 得到新的标记状态集合, 判断是否仍存在不可诊断语言, 得到当前的标记可诊断性。

在当前的模型上, 构建可诊断性判断所需的预诊断器。在预诊断器上, 增量判断可诊断性。预诊断器构建步骤如下:

(1)消去模型中的不可观测事件:用可观测投影, 将模型中的不可观测事件抹去。

(2)建立模型在可观测事件驱动下的状态可达关系:将已经抹去不可观测事件的转移消去, 仅保留可观测事件的转移, 得到观测自动机。

(3)在状态中加入故障标签:从标记状态集合向前传递故障, 得到不同的故障标签, 当状态存在多个故障标签时, 表示当前语言是不可诊断的。

接下来, 对构建过程进行形式化的定义和详细叙述。

定义9(观测模型) 观测模型是一个五元组G₀=(Q_o, E_o∪ {ε }, T_o, I_o, M_o), 其中Q_o=I∪ {q|q'× e× q, e∈ E_o}, T_o⊆Q_o× E_o× Q_o, I_o=I, M_o=M∩ Q_o。

观测模型得到的实际是仅保留观测事件及相应状态的自动机模型, 图1是模型及其对应的观测模型的例子。观测模型是一个不确定状态自动机, 一个状态可能被多个事件所触发, 但是实际上是不同的语言。用故障标签进行部分的区分。故障标签是状态的一种扩展, 表示在当前状态下, 前向或后向可能存在的故障。由于采用逆向的故障标签编译方法, 本文的故障标签表示的是在当前状态下, 后续可能出现的故障。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 自动机模型及可观测模型Fig.1 Automaton and observable automaton

扩展状态, 加入故障标签:观测模型中的状态集合被扩展为状态与任意长度的故障事件的乘积:Q_p=Q_o× B, 其中B是状态的故障标签位, 每一个状态从后续状态中获得故障标签, 状态的故障标签记为b(q)。给出一个简单算法, 反向得到故障标签。

实际上, 故障标签从终止状态向初始状态传播, 每个具有多个触发事件的状态, 都判断其后状态的故障标签, 如果故障标签相同, 则认为后续的故障是一致的, 可以作为当前状态的唯一标签; 如果故障标签不同, 则认为后续存在多个故障标签, 将故障标签并列, 得到当前状态的多个标签。

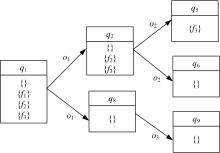
最后得到带有故障标签的观测模型, 称为预诊断器。增量方法在观测模型上展开, 根据观测窗口, 判断故障标签, 决定是否剪枝或等待下一次增量。图2为带有故障标签的观测模型, 即预诊断器。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 预诊断器Fig.2 Pre-diagnoser

故障标签传播算法

输入: 可观测模

G_o=(Q_o, E_o∪ {ε }, T_o, I_o, M_o)

输出:预诊断器G_p=(Q_p, E_o, T_o, I_o, M_o)

初始化: M_o=M_o× ⌀, i=0

While M_i≠ I_o do

∀ q∈ M_i, ∀ q', q× e× q'∈ T

If b(q')⊆b(q)

b(q)=b(q)∪ P_f(e)

If b(q')∩ b(q)=⌀ then

b(q)=b(q)∪ b(q')∪ P_f(e)

M_i+1=M_i∪ {q'}-{q}

i+1

∀ q∈ I_o, q× e× q'∈ T

If b(q')⊆b(q) then

b(q)=b(q)∪ P_f(e)

If b(q')∩ b(q)=⌀ then

b(q)=b(q)∪ b(q')∪ P_f(e)

增量方法在带有故障标签的观测模型上进行, 是一种半在线方法。半在线是指整体运行过程中, 既存在离线行为, 也存在在线行为。可诊断性判定的增量离线部分, 是指离线进行可诊断性判定及剪枝的过程; 在线部分则是得到观测窗口并更新当前标记状态集合的过程。

离线的可诊断性结果是确定的, 在整体模型中, 可诊断性的结果有且只有唯一一个。在线的可诊断性结果是不确定的, 在整体模型中, 虽然在线过程结束后的可诊断性结果是确定的, 但是在线过程进行时, 可诊断性随着观测窗口的出现在不断改变。某些语言由于具有相同的前缀, 在增量到达一定阈值之前是不可诊断的, 而当增量观测窗口达到必要长度之后, 这些语言能够被区分开来, 则这些语言被判定为可诊断的, 并且之后一直将是可诊断的。可诊断性的这种特点被称为可诊断性的连续性。

根据可诊断性的连续性, 增量方法可以对已经判定出可诊断性结果的语言在模型中进行剪枝, 而无需考虑是否可诊断性会被改变。语言是模型中的一条轨迹上的全部事件序列, 在判断剪枝时, 考虑如下问题:

(1)当前状态是否是唯一的未区分状态, 若是, 则根据故障标签判断是否需要进一步增量; 若否, 则与其他状态用增量窗口进行区分。

(2)根据当前状态的故障标签, 可诊断性地判定。如果当前的故障标签是唯一的, 根据逆向生成故障标签的算法, 可知当前状态之后的故障是否相同。若当前故障唯一, 则判为可诊断并且从当前状态开始剪枝。如果当前故障标签不唯一, 可知当前状态之后还可能存在出现多个不可诊断语言的情况, 则不能剪枝。

(3)剪枝后, 更新标记状态集合。若当前状态被剪枝, 则标记为终止状态; 若当前状态未被剪枝, 则根据观测窗口更新当前状态。

观测窗口在增量判定可诊断性的过程中, 是一个虚拟的在线过程。实际在线过程中, 观测窗口的出现是离散的。而在本文增量过程中, 观测窗口在确定的时间, 以确定的大小出现, 用于保证判定可诊断性的过程始终在一个较小的区域内进行, 避免在较大规模的模型中进行判断产生的指数级扩展。观测窗口的大小是可控的, 其大小根据经验在[1, |E_o|]上取值。具体大小依赖于模型的观测长度、重复度等。

观测窗口到达时, 预诊断器首先判断标记可诊断性, 并根据剪枝规则进行剪枝, 更新标记状态, 最后根据当前状态判断是否可诊断性被全部确定, 决定等待下一个观测窗口或返回全局的可诊断性结果。

给出一个增量判断可诊断性的算法, 用在预诊断器上, 用确定大小的观测窗口进行增量的可诊断性判定。

增量可诊断性判定算法描述的是一个增量判定可诊断性的过程, 将观测事件拆分为窗口进行可诊断性的增量判定。观测窗口到来时, 如果当前的标记状态集合已经是空集, 代表全部语言的可诊断性判定完毕, 不需要增量的观测。而当前标记状态集合不是空集, 则表示还需要继续判定可诊断性。

增量可诊断性判定算法

输入:预诊断器

G_p=(Q_p, E_o× B, T_o, I_o, M_o),

W=< w₁, w₂, …, w_n>

输出:可诊断性结果:D(G)={true, false}

初始化:i=0

While w_i≠ ⌀ do

If M_i≠ ⌀ then

L_i=Test(M_i, w_i), M_i+1=Update(M_i, w_i)

If ∃l_j∈ L_i, Conf(l_j, w_i) then

If ∃q∈ l_j∩ M_i+1, String(b(q)) then

D(l_j, P_f(l_j))=true

M_i+1=M_i+1-q

Else

M_i+1=M_i+1

Else

If ∀ q, q'∈ L_j∩ M_i+1, b(q)=b(q')

D(l, P_f(l))=true

D(l', P_f(l'))=true

M_i+1=M_i+1-{q, q'}

Else

M_i+1=M_i+1

If M_i≠ ⌀ then

D(G)=false

Else

D(G)=true

在增量窗口到达时, 根据当前标记状态和观测窗口进行一致性的判定和标记状态的扩展, 一致性是指:在当前的标记状态集合下, 哪些语言是可以被观测窗口扩展并且不可诊断的; 在当前标记状态基础上, 根据观测窗口, 进行标记状态的扩展。

增量扩展中, 存在4种情况, 分别处理如下:

(1)观测能将某些轨迹直接与其他轨迹区分, 并且当前状态不存在多个故障标签。这代表当前轨迹已经与其他轨迹区分, 并且之后不存在分支或者分支上的故障相同。因此, 在当前状态剪枝, 不进行扩展, 把当前状态从待扩展的标记状态集合中删除。

(2)观测能够将某些轨迹直接与其他轨迹区分, 但是当前状态存在多个故障标签。这代表当前轨迹即使能与其他轨迹区分, 但是之后存在带有不同故障的分支, 还需要进一步判定。因此, 保留当前的状态, 等待增量扩展。

(3)观测不能直接区分当前轨迹, 但是当前状态具有相同的故障标签。这表示当前的轨迹虽然不能被区分, 但是所有的后续轨迹均具有相同的故障, 因此这些轨迹是可诊断的。

(4)观测不能直接区分当前轨迹, 并且故障标签不同。这表示当前轨迹不可诊断, 因此等待进一步的增量。

在上述分支过程中, 凡是可诊断的状态均被删除, 当标记状态集合为空时, 模型可诊断。否则, 当增量过程结束后, 模型不可诊断。

图3给出了增量可诊断性判定的过程。当观测窗口w₂与状态q₈冲突, 并且状态q₈的故障标签唯一, 因此状态q₈被剪枝。不冲突的状态q₂被扩展, 得到状态q₅、q₆, 这两个状态不能被现有的观测区分, 并且两个状态的故障标签不同, 因此被标记状态集合保留, 标记状态集合不为空, 则当前系统不可诊断。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 增量可诊断判定过程Fig.3 Incremental process in determining diagnosability

观测事件和故障事件占全部事件的比例通常是由物理系统的设计决定的, 观测事件集合通常是由外部可观测的事件和内部传感器探测的事件组成。而故障事件集合是由系统中可能存在的故障组成。因此, 一旦设计完成, 建模过程不能改变这些因素。也就是说, 对于特定的系统, 这个比例是固定的。

观测事件的重复度以及观测序列的长度与物理系统的设计有关, 但是也与建模过程有关。在物理系统中, 重复的观测是取自不同传感器的相同类型观测, 而在建模过程中, 可以认为这些事件是相同的, 也可以认为是不同的。观测序列长度随物理系统运行过程逐步增加, 但是建模过程中, 可以通过不同的编译方法将观测序列长度降低。在上述因素的影响下, 模型及可诊断性存在如下性质:

性质1 ∃l, l'∈ L(G), ∃n₁, n₂∈ N, ∃obs₁=P_o(l), ∃obs₂=P_o(l'), l'=pre(l), |obs₁|=n₁, |obs₂|=n₂, n₁> n₂, D(l', f)=true⇒ D(l, f)=true。

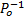
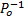
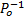
证明 当D(l', f), 表示当前语言是可诊断的, 往证当观测长度增加时, 不影响可诊断性。若D(l', f)=true, 则∀ l_i, l_j∈ (P_o(l')), P_f(l_i)=P_f(l_j)。当观测长度增加时, P_o(l)=P_o(l')obs, 并且已知l'=pre(l), 令L₁= (P_o(l)), L₂= (P_o(l'))由于l是在l'上扩展而来, 当存在增量观测时, 可能存在着剪枝过程, 因此L₁⊆L₂, 已知l'是可诊断的, 那么∀ l_i∈ L₂, D(L_i, f)=true, f∈ P_f(l'), 得到l_j∈ L₁, P_f(l_j)=P_f(l')。所以∀ l_j, l_k∈ L₁, P_f(l_j)=P_f(l_k)。因此, l是可诊断的。观测长度增加时, 不影响可诊断性。

性质2 当前状态被剪枝, 与经由当前状态的全部语言可诊断是等价的。

证明 若当前状态被剪枝, 则当前状态q满足:状态与新增窗口冲突, 并且|b(q)|=1; 或者状态与新增窗口不冲突, 但是b(q)=b(q')。

若状态与新增窗口冲突, 可以触发当前状态的观测事件o不在新增窗口w_i中, o将经由状态q的语言与其他语言区分; 当状态的故障标签唯一时, 表示当前状态后的轨迹中仅存在唯一的一类故障。则经由状态q的语言均可以被映射到同样的一个故障集合上, 则经由当前状态的语言可诊断。

若状态与新增窗口不冲突, 任意不冲突的状态q', b(q)=b(q'), 当前状态可以被新增窗口所扩展。但是由于当前状态以及全部可以扩展的状态中的故障标签相等, 可以被映射到相同的故障集合上, 故经由当前状态的语言可诊断。

在文献[6]提出的测试集合上进行扩展实验, 实验设备的处理器为英特尔双核2.80 GHz, 内存1 GB。测试如下两个问题:

(1)测试增量方法的效率:测试在固定大小窗口下, 增量方法与非增量方法的可诊断性判定效率, 结果如图4(a)所示。

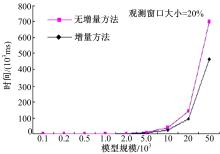
(2)测试窗口大小对可诊断性判定效率的影响, 结果如图4(b)所示。

由实验结果可知, 当增量窗口在适当的大小时, 增量可诊断性测试的效率较高。而当窗口过大或者过小时, 增量可诊断性测试的效率降低。

图4

Fig.4

	Figure Option ViewDownloadNew Window
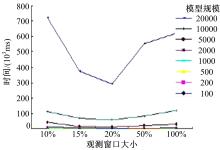	图4 实验结果（a）增量方法效率对比Fig.4 Experiment result

图4

Experiment result (b)窗口大小对效率的影响

	Figure Option ViewDownloadNew Window
	图4 实验结果Fig.4

提出一种加速可诊断性判定的方法, 通过逆向提取故障标签, 在诊断器中正向判断可诊断性, 根据故障标签判断条件, 提供剪枝信息, 加速可诊断性判定。在进一步的工作中, 将增量诊断、增量窗口与可诊断性判定结合, 改进在线诊断效率, 并为不完备事件的发现和建模提供诊断依据。