引用本文
李占山, 贾湘华, 许苍竹, 张舒娟. 基于论域折半的最大限定路径相容算法. 45(1): 229-235
LI Zhan-shan, JIA Xiang-hua, XU Cang-zhu, ZHANG Shu-juan. Max-restricted path consistency algorithm based on half range of domain. Journal of Jilin University Engineering and Technology Edition, 45(1): 229-235  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于论域折半的最大限定路径相容算法
李占山1,2, 贾湘华1,2, 许苍竹1,2, 张舒娟1,2
1.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012
2.吉林大学 计算机科学与技术学院,长春 130012

作者简介:李占山(1966-),男,教授,博士.研究方向:约束求解,模型诊断,智能规划与调度.E-mail:zslizsli@163.com

基金:国家自然科学基金项目(61170314,61272208); 吉林省自然科学基金项目(20140101200JC)
摘要

针对绝大多数不可满足问题的特点,提出了一种将弧相容算法与最大限定路径相容算法相结合的相容性算法——基于论域折半的最大限定路径相容的算法。该算法充分利用了弧相容计算开销小和最大限定相容删值能力强的优点,可以减少在求解不可满足问题中生成的结点数,进而提高求解效率。实验结果表明,本文算法在处理不可满足问题时的求解效率明显优于传统的维持弧相容算法。

关键词: 人工智能; 论域折半; 弧相容; 最大限定路径相容; 不可满足问题
中图分类号:TP18 文献标志码:A 文章编号:1671-5497(2015)01-0229-07
Max-restricted path consistency algorithm based on half range of domain
LI Zhan-shan1,2, JIA Xiang-hua1,2, XU Cang-zhu1,2, ZHANG Shu-juan1,2
1.Key Laboratory of Symbolic Computation and Knowledge Engineering for Ministry of Education, Jilin University, Changchun 130012,China
2.College of Computer Science and Technology, Jilin University, Changchun 130012,China
Abstract

A new algorithm is proposed, which combines arc consistency algorithm and max-restricted path consistency algorithm. The new algorithm makes full use of the low computation cost of arc consistency and the strong ability to remove invalid values of the max-restricted path consistency, thus reducing the visited nodes when coping with unsatisfied problems. As a result, the efficiency can be improved. Experiment results show that the proposed max-restricted path consistency algorithm based on the half range of domain outperforms the traditional maintaining arc consistency algorithm by large margin when solving the unsatisfied problems.

Keyword: artificial intelligence; half range of domain; arc consistency; max-restricted path consistency; unsatisfied problems
引言

约束满足问题(Constraint satisfaction problem, CSP)是人工智能的一个重要分支, 相关技术可以广泛应用于组合问题和数据库等领域, 求解约束满足问题的关键在于证明该问题无解或找到问题的解。回溯搜索算法是求解约束满足问题最为广泛的完备算法。对于可满足问题, 该算法可以找到问题的一个解或者多个解; 对于不可满足问题, 则可以证明问题无解。

传统的回溯搜索算法尽管能够求解约束满足问题, 然而当问题规模比较大时, 采用传统的回溯搜索算法往往会导致搜索空间过大, 容易引发“ 组合爆炸” , 求解效率极其低下。在回溯搜索的框架下嵌入合适的相容性算法是有效防止“ 组合爆炸” 的常用方法, 因此近几年很多学者都致力于相容性算法的研究。为了解决因搜索空间过大而导致求解效率低这一问题, MAC算法[1, 2]最先被提出, 并广泛应用于各类CSP求解器中。该算法通过在回溯搜索算法中嵌入AC算法[3, 4, 5], 在预处理和搜索解过程中均维持网络弧相容, 从而能保证实例化变量前将当前的搜索空间压缩到一定值, 进而提高求解效率。弧相容算法通过删除约束网络中不满足弧相容性质的变量值, 在一定程度上压缩搜索空间。随着相容性算法研究的深入, 一些删值能力更强的相容性算法相继被提出, 备受关注的是SAC[6](Singleton arc consistency)和max-RPC[7, 8](max-restricted path consistency)。在这两种强相容性算法中, SAC对论域的删值能力严格强于AC和max-RPC。但对某约束网络单独使用SAC作为内嵌的相容性算法时, 计算开销比较大, 所以通常SAC仅用于求解的预处理阶段, 或者仅对网络中极少部分的变量值在搜索过程中维持SAC性质[9]。相比之下, 删值能力和计算开销介于AC和SAC之间的max-RPC则是AC与SAC算法的一个很好的折衷。然而仅将max-RPC作为唯一的相容性算法内嵌于回溯搜索算法框架下同样不能取得很好的效果。因此, 对于max-RPC, 很多学者致力于寻找一种介于max-RPC和AC之间的相容性算法, 进而得出一种相对高效的求解算法。比较有代表性的算法是轻量级版的Lmax-RPC[10], 该算法的缺陷在于对网络执行Lmax-RPC后得到的网络并不像max-RPC那样稳定, 其网络最终形态与约束传播队列中元素的排列顺序存在一定关系, 不能得到唯一的网络闭包。

本文提出了删值能力介于AC和max-RPC之间的稳定算法Hmax-RPC(Half max-restricted path consistency), 通过对约束网络执行该算法, 可以得到唯一的网络闭包, 且能高效地求解不可满足问题。本文首先介绍了CSP的相关背景知识, 提出并分析了Hmax-RPC的基本思想, 并利用该算法对随机抽取的多类Benchmark标准用例做了相应的实验测试, 结果表明在处理不可满足问题上本文方法具有明显求解优势。

1 背景知识

定义1[11](约束网络)

约束网络 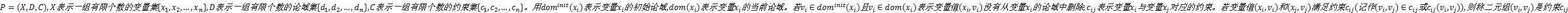的一个关系。

定义2(弧相容AC)

约束 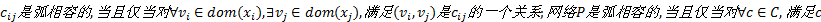是弧相容的。

性质1 若 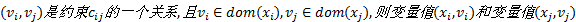互为AC支持。

定义3(最大限定路径相容max-RPC)

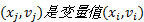
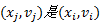
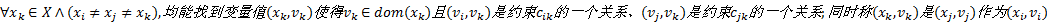
变量值 的一个PC支持, 当且仅当 的AC支持且对 PC支持的PC证人。

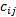
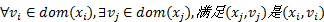
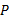
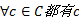
约束 满足max-RPC, 当且仅当对 的PC支持; 约束网络 满足max-RPC, 当且仅当对 满足max-RPC。

性质2 max-RPC的相容性严格强于AC。

定义4[11](等价约束网络)

约束网络的解表示对网络中所有变量的一组赋值均满足该约束网络中所有的约束条件, 记作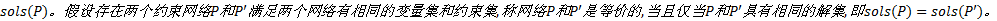

定义5[11](合并稳定性)

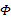
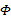
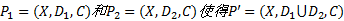
假设 为某个基于定义域的局部相容, 称 满足合并稳定性, 当且仅当对任意满足Φ -相容的网络 是Φ -相容的。

定义6[11](Φ -闭包)

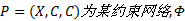
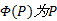
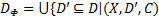
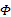
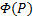
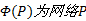
假设 为某个基于定义域的局部相容, 令 的一个子网络, 满足 满足Φ -相容}。若 满足合并稳定性且 是唯一的, 则称 的Φ -闭包。

性质3 设 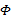为AC、max-RPC或SAC中的任意一个局部相容, 网络P存在唯一的Φ -闭包。

2 Hmax-RPC算法的思路及伪代码
2.1 基本思路

求解不可满足问题的最终目标是证明问题无解。在传统回溯搜索算法中嵌入弧相容算法后得到MAC算法, MAC算法将问题的求解分为两个部分:预处理部分和搜索部分。预处理部分主要是对整个约束网络进行搜索(即实例化变量)之前, 将不满足弧相容的变量值预先从网络中删除。如果在预处理过程中导致某个变量的论域被删空, 则无需生成任何结点即可证明问题无解; 如果约束网络顺利通过预处理阶段, 则待求解的问题将生成对应的搜索树, 此时证明问题无解的方法则是当前的结点为根结点时, 如果仍需要回溯, 则可证明问题无解。

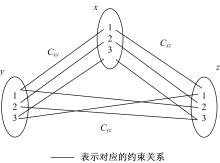
MAC算法比传统的回溯搜索算法明显具有更高的求解效率。然而, 由于继AC算法之后相容性更强的算法被提出, 包括SAC和max-RPC。这些算法较AC算法而言具有更强的论域过滤能力。但是由于SAC的计算开销过大, 很少直接将其完全内嵌到回溯搜索算法中。而max-RPC在删值能力和计算开销两方面性能介于AC与SAC算法之间。如果在整个求解过程中始终都嵌入max-RPC算法, 计算开销仍然比较大, 而且很多变量论域中的值只需保持在AC层面即可快速求解问题。在搜索过程中, 由于最初待赋值的几个变量在赋值时非常关键, 如果这些变量值不可能成为解的一部分, 则之后的所有其他变量赋值都是无效的, 图1说明了这一问题。

图1 约束网络PFig.1 Constraint network P

图1表示某约束网络P, 由定义2和定义3知, 网络P中的所有约束都满足AC, 但是均不满足max-RPC, 因而对该网络中的任意变量值, 由于其不满足max-RPC, 必然不能成为解的一部分, 即在求解时, 不能将该变量值赋值给其对应的变量。然而这些变量值都满足AC, 如果在预处理阶段采用AC, 预处理之后这些变量值均不会从对应的论域中删除; 若采用max-RPC, 则这些变量值在预处理之后都会被删除, 可直接证明问题无解, AC则需要进入搜索阶段才能证明问题无解。

综合上述观点可知, 对每个变量论域的前半部分采用更强的过滤算法是必要的, 因为若某个变量的前半部分因不满足max-RPC被删除后, 通过约束传播, 可直接对该变量自身的后半部分论域及网络中与该变量具有约束关系的其他变量的论域产生一定的影响。而绝大多数的不可满足问题, 在运用相容性技术之后只需尝试用变量的前半部分值实例化变量失败后受约束传播的影响即可证明问题无解, 因此对应后半部分无需再搜索。后半部分维持一定性质, 无需更强的过滤(因为如果变量论域的后半部分也维持更强的过滤性质, 则会产生更多的不必要的计算开销)。基于此观点, 本文提出了Hmax-RPC。主要思想是:在预处理和搜索阶段, 每个变量论域的前半部分维持max-RPC, 而后半部分则维持AC, 这样既能在变量论域的前半部分删除较AC而言更多的变量值, 又能使后半部分具有与AC相同的时间开销。正是由于前半部分删除了更多的无效的变量值, 导致整个问题尤其是不可满足问题具有整体更优的求解效率。

2.2 伪代码

Hmax-RPC算法的伪代码表示如下:

Function Hmax-RPC(X, D, C)):Bool

1 Q← Q∪ {(c, x)|c∈ C, x∈ scp(c)};

2 while Q≠ ∅ do

3 select and remove (c, x) from Q;

4 if revise_H(c, x) then

5 if D(x)=∅ then return false;

6 else

7 Q← Q∪ {(c1, y)|c1∈ CΛ c≠ c1Λ y≠ xΛ x∈ scp(c)};

8 return true

Function revise_H(c, xi):Bool

1 change← false;

2 foreach vi∈ dom(xi) do

3 if position(xi, vi)< =|dominit(xi)| /2 then

4 if seekPCSupport(c, xi, vi)=false then

5 change=true;

6 remove vi from dom(xi);

7 else

8 if seekACSupport(c, x, vi) =false then

9 change=true;

10 remove vi from dom(xi);

11 return change;

Function seekACSupport(c, xi, vi):Bool

1 {xj}← scp(c)/{xi}; //c为二元约束, scp(c)={xi, xj}

2 foreach vj∈ dom(xj) do

3 if cij(vi, vj) then

4 return true;

5 return false;

Function seekPCSupport(c, xi, vi):Bool

1 {xj}← scp(c)/{xi};

2 Link← {xk|cik∈ C and cjk∈ C};

3 foreach vj∈ dom(xj) do

4 if cij(vi, vj) then

5 foreach xk∈ Link do

6 vk← nil;

7 while vk≠ last(dom(xk)) do

8 vk← next(dom(xk), vk);

9 if cik(vi, vk) and cjk(vj, vk) then return true;

10 return false;

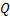
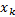
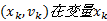
上述代码中 表示传播队列, revise_H(c, x)用于修正约束 寻找PC支持、AC支持。last(dom(xk))表示变量 论域的最后一个位置, next(dom(xk), vk)表示变量值 论域中的下一个变量值。

3 Hmax-RPC算法执行步骤及定理证明
3.1 执行步骤

步骤1 将所有的约束及对应变量构成的c-value加入到传播队列中。

步骤2 依次从传播队列中取出并修正传播队列中的c-value。并为相应变量中的所有变量值查找支持, 具体如下:①若变量值位于变量论域的前半部分, 则为该变量值查找PC支持。在查找PC支持时, 需要先查找变量值在对应约束上的AC支持, 再查找与之相关的PC证人(定义3)。如果相应的AC支持和PC证人均能找到, 则说明该变量值查找到PC支持; ②若变量值位于变量论域的后半部分, 则为该变量查找AC支持。

步骤3 若某个变量值未能找到支持, 则将该变量值从对应的变量论域中删除, 并传播由于该变量论域的变化对其他变量的影响, 即将所有相关的其他约束与对应变量构成的c-value加入到传播队列 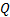中。

步骤4 重复执行步骤2、3直至传播队列为空。若在整个过程中某个变量论域被删空, 则返回false; 若整个过程中始终没有变量论域被删空, 则返回true。

3.2 相关定理及证明

定理1 Hmax-RPC的相容性强度介于AC与max-RPC之间。

证明 假设存在约束网络 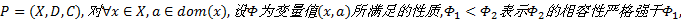则:

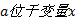
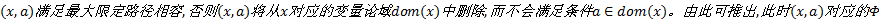
(1)若 论域的前半部分, 由函数revise_H(c, xi)对应代码的第3~6行可知, 变量值 满足:Φ =max-RPC。

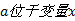
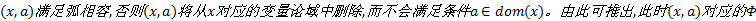
(2)若 论域的后半部分, 由函数revise_H(c, xi)对应代码的第8~10行可知, 变量值 满足:AC=Φ < max-RPC。

(3)若某约束网络 满足AC(或max-RPC), 则对 满足AC(或max-RPC)。

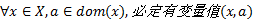
综合(1)(2)(3)和性质2可知, 对变量 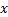的整体论域而言, AC< Hmax-RPC< max-RPC, 即Hmax-RPC的相容性强度介于AC与max-RPC之间。

定理2 MHmax-RPC(Maintaining half max-restricted path consistency)是完备的求解算法。

证明 由定理1可知, Hmax-RPC的相容性强度介于AC与max-RPC之间, 而MAC和Mmax-RPC均为完备算法, 即如果某个变量值不满足AC(或max-RPC), 则该变量值必定不能成为解的一部分, 可以在实例化之前将该变量从对应的论域中删除。

任何不满足Hmax-RPC的变量值必定不满足max-RPC, 因而该变量值不能成为解的一部分, 将这些变量值在实例化之前从对应的论域中删除是合理的。所以, 利用Hmax-RPC过滤变量论域不会改变约束网络解的性质, 即不会将可能成为解的一部分变量值删除, 由定义4可得, 经Hmax-RPC过滤后得到的必然是过滤前网络的一个等价网络。

综上可知, 利用Hmax-RPC作为相容性算法嵌入到回溯搜索算法中得到的MHmax-RPC算法可以找到约束满足问题的解或者证明问题无解, 因而MHmax-RPC是完备的求解算法。

定理3 每一个约束网络存在唯一的Hmax-RPC-闭包。

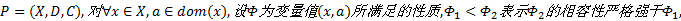
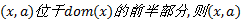
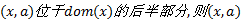
证明 假设存在约束网络 则:①若变量值 必定满足max-RPC, 此时Φ =max-RPC; ②若变量值 必定满足AC, 此时Φ =AC。

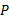
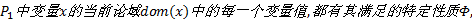
所以, 对初始网络 执行完Hmax-RPC后, 得到的网络P1=Hmax-RPC(P), 对于 由①②和性质3可知, 约束网络存在唯一的Hmax-RPC-闭包。

4 实验结果及其分析

将Hmax-RPC嵌入到回溯搜索算法框架中得到MHmax-RPC算法, 并与最为广泛使用的MAC算法针对不同的Benchmark标准测试用例求解结果进行对比。在求解过程中, 两种算法中均采用了dom/wdeg[12]变量排序启发式, 以提高整体的求解效率, 算法均采用字典序的值启发式。程序运行在32位win7操作系统下, 编程语言为C++, 编译环境为VS2010, 硬件为Intel(R) Core(TM)2 Duo、E6750@2.66GHz型号的CPU, 2.00 G内存。实验所选取的测试用例对应为二元约束网络, 用例在http://www.cril.univ-artois.fr/~lecoutre/index.html获取。实验测试结果如表1所示。

表1的第1列中的sat、unsat分别表示可满足问题和不可满足问题, #n表示随机抽取该系列问题中的不同测试用例的个数为n, 第2列中的arg_time(s)表示这n个测试用例的CPU平均运行时间, s表示时间单位秒, arg_vnodes表示这n个测试用例在求解过程中对应搜索树的平均生成结点个数。

在求解可满足问题时, 从表1中的Driver系列、frb-15系列、frb-17系列、RLFAP-scensMod系列对比可以看出, MHmax-RPC的生成结点个数少于MAC, 因为根据定理1, Hmax-RPC的相容性强度介于max-RPC与AC之间, 所以在每一个变量的前半部分论域(也是求解过程中最关键的部分), MHmax-RPC删除的变量值的个数大于或等于MAC删除的变量值的个数, 根据定理2, 这些被删除的变量值不可能成为解的一部分。因此, MHmax-RPC较MAC多删除的结点减少了在找到问题解之前生成无效的子树个数, 这些无效的子树的任何一条路径最终必定会产生死结点(dead-end)。然而, 尽管在处理这些系列问题时能够生成更少的结点, 但是从本文2.2部分的函数seekACSupport(c, xi, vi)和函数seekPCSupport(c, xi, vi)的运行流程可以看出, seekPCSupport(c, xi, vi)多出的第5~9行需要为每一对互为AC支持(性质1)的元组查找相关的PC证人, 当与元组相关的两个变量的公共变量个数较多时, seekPCSupport(c, xi, vi)的时间开销远大于seekACSupport(c, xi, vi), 这种情况下, 若网络中相应约束的紧度比较小[13], 其中的约束对应的许多关系既满足PC性质, 又满足AC性质, 此时MHmax-RPC在寻找PC支持较寻找AC支持多花费的时间比减少搜索空间所节省的

表1 实验测试结果 Table 1 Experimental results

时间多, 从而使得在上述测试用例系列中整体时间效率不如MAC高。对于BQWH-15-106系列和BQWH-18-141系列, 由于MHmax-RPC通过减少搜索空间所节省的时间比较多, 而seekPCSupport(c, xi, vi)较seekACSupport(c, xi, vi)多花费的时间相对比较少, 所以在BQWH-15-106和BQWH-18-141两系列问题上, MHmax-RPC在平均生成结点数和平均耗时量上均少于MAC。

在求解不可满足问题时, 若MAC在预处理阶段即可证明问题无解, 此时MAC的求解效率必然高于MHmax-RPC, 因为在这种情况下, 生成的结点数都是0, 每个论域的前半部分MHmax-RPC寻找PC支持所耗费的时间大于MAC中寻找AC支持的时间, 使得整体上MAC所花费的时间少于MHmax-RPC。所以表1中的sat系列RLFAP-graphs, 由于MAC在预处理阶段即可将RLFAP-graphs系列对应的约束网络中某个变量的论域删空, 使得MAC在预处理阶段即可证明对应约束网络的无解, 所以求解RLFAP-graphs系列对应的约束网络时, MAC与MHmax-RPC生成的平均结点个数均为0, 而时间上MAC少于MHmax-RPC。对于大多数的不可满足问题, 利用MAC算法求解时, 通常要进入搜索阶段才能证明问题无解, 此时分以下两种情况:

(1)若执行完预处理阶段后, AC(P)≠ ⊥而Hmax-RPC(P)=⊥, 此时MAC需要进入搜索阶段才能证明问题无解, 而MHmax-RPC只需要在预处理阶段即可证明问题无解。如表1中的RLFAP-scens系列, MAC的平均生成结点数为3.60, 而MHmax-RPC的平均生成结点个数为0; 对于composed-25-1-25, composed-25-1-40, composed-25-1-80这3个系列, 利用MAC的平均生成结点个数为100~300, 而用MHmax-RPC求解时, 平均生成结点个数为0~1, 说明这4个系列均存在采用MHmax-RPC作为求解算法时仅在预处理阶段即可证明问题无解的部分测试用例, 而这4个系列中剩下的实例在求解过程中生成的结点个数为1~10。

(2)若执行完预处理阶段之后, AC(P)≠ ⊥且Hmax-RPC(P)≠ ⊥, 说明测试用例对应的约束网络P利用MAC和MHmax-RPC求解均需要进入搜索阶段。在搜索阶段, 由于MHmax-RPC删除了较MAC更多且不能成为解部分的变量值, 而这些变量值的删除经约束传播后会导致更多与之相关的其他变量值被删除, 使得算法在搜索过程中能更快地回溯至根结点, 在根结点处继续回溯后, 便能证明问题无解。表1中的composed-25-1-2、composed-75、dual_ehi-85、dual_ehi-90、BH-4-4、qcp-10、RLFAP-graphsMode等系列均为此情况, 这些系列平均生成的结点个数均大于1, 且在求解这些系列中的实例时, MHmax-RPC的求解效率高于MAC。

通过以上实验结果对比分析, 可以得出:在求解绝大多数不可满足问题时, MHmax-RPC较MAC明显具有更高的求解效率。

由于Hmax-RPC是弧相容(AC)与最大限定路径相容算法(max-RPC)的一种折衷算法, 根据定理1, Hmax-RPC的相容性介于AC与max-RPC之间, 所以执行一次Hmax-RPC的时间开销一般高于AC, 而Hmax-RPC的删值能力弱于max-RPC。因此, max-RPC仅适用于求解过程中的预处理阶段, 在求解阶段, AC一般适用于求解可满足问题, Hmax-RPC一般适用于求解不可满足问题。

5 结束语

针对约束满足问题求解的特点, 提出了基于论域折半的最大限定路径相容算法Hmax-RPC。Hmax-RPC是一种稳定的相容性算法, 约束网络通过执行该算法, 能够得到唯一的网络闭包, 实验结果表明, 将Hmax-RPC嵌入到回溯搜索算法中得到的MHmax-RPC算法, 在处理不可满足问题时, 求解效率明显高于常用的MAC算法。但由于算法采用的是弧相容算法和最大限定路径相容算法的一种平衡思想, Hmax-RPC的时间开销高于AC, 在处理绝大多数可满足问题时, MHmax-RPC比MAC求解效率更低, 因而MHmax-RPC对于各类问题的求解不具有普遍适用性。未来的工作将考虑在问题求解的预处理部分嵌用max-RPC, 而搜索部分则根据问题的可满足性来选择AC或Hmax-RPC, 进而提高算法的求解效率和适用性。

The authors have declared that no competing interests exist.

参考文献
[1] Sabin Daniel, Freuder Eugene C. Contradicting conventional wisdom in constraint satisfaction[C]∥Proceedings of CP, Rosario, Orcas Island , Was- hington, 1994: 10-20. [本文引用:1]
[2] Likitvivatanavong Chavalit, Zhang Yuan-lin, Bowen James, et al. Arc consistency during search[C]∥Proceedings of IJCAI, India: Morgan Kaufmann, 2007: 137-142. [本文引用:1]
[3] Mackworth Alan K. Consistency in networks of relations[J]. Artificial Intelligence, 1977, 8(1): 99-118. [本文引用:1] [JCR: 2.194]
[4] Christophe Lecoutre, Fred Hemery. A study of residual supports in arc consistency[C]∥Proceeding of IJCAI, 2007: 125-130. [本文引用:1]
[5] Christophe Lecoutre, Julien Vion. Enforcing arc consistency using bitwise operations[J]. Const- raint Programming Letters, 2008(2): 21-35. [本文引用:1]
[6] Romuald Debruyne, Christian Bessiere. Some practical filtering techniques for the constraint satisfaction problem[C]∥Proceedings of IJCAI, 1997: 412-417. [本文引用:1]
[7] Romuald Debruyne, Christian Bessiere. From restricted path consistency to max-restricted path consistency[C]∥Proceedings of CP, 1997: 312-326. [本文引用:1]
[8] Thanasis Balafoutis, Anastasia Paparrizou, Kostas Stergiou, et al. New algorithms for max restricted path consistency[J]. Constraints, 2011, 16(4): 372-406. [本文引用:1] [JCR: 0.737]
[9] Christophe Lecoutre, Patrick Prosser. Maintaining singleton arc consistency[C]∥Proceedings of CPAI, 2006: 47-61. [本文引用:1]
[10] Julien Vion, Romuald Debruyne. Light algorithms for maintaining max-RPC during search[C]∥Proceedings of SARA, 2009. [本文引用:1]
[11] Possi Francesca, Van Beek Peter, Walsh Toby. Hand book of Constraint Programming[M] . New York: Elsevier, 2006: 13-29. [本文引用:4]
[12] Frédéric Boussemart, Fred Hemery, Christophe Lecoutre, et al. Boosting systematic search by weighting constraints[C]∥Proceedings of ECAI, 2004: 146-150. [本文引用:1]
[13] 李占山, 张良, 郭劲松, 等. 基于问题结构的边界启发式方法[J]. 吉林大学学报: 工学版, 2013, 43(5): 1045-1051.
Li Zhan-shan, Zhang Liang, Guo Jin-song, et al. Boundary heuristic based on problem structure[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(4): 1045-1051. [本文引用:1] [CJCR: 0.701]