作者简介:黄宏涛(1980-),男,副教授,博士.研究方向:模型检测.E-mail:huanghongtao@outlook.com
惰性切片是一种有效的状态空间缩减方法,但是它无法直接判定一个模型是否满足所期望的线性时间性质。针对该问题,提出了一种基于惰性切片的线性时态逻辑公式验证方法。该方法首先构造给定线性时态逻辑公式的否定Büchi自动机与系统模型的乘积自动机,然后使用惰性切片算法在该乘积自动机上以惰性方式搜索可接受迹,从而把线性时间性质验证问题转换为通过可达性分析搜索可接受状态的不变性检测过程。实验结果证明,基于惰性切片的线性时态逻辑公式验证算法在不损失验证结果正确性的前提下使惰性切片算法具备了验证线性时间性质的能力,同时也有效提高了LTL模型检测方法的可扩展性。
Lazy slicing is an effective state-space reduction method, but it can not directly determine whether a model satisfies the expected linear property. A lazy slicing based method is proposed to solve this problem. First, it constructs a negation Büchi automaton for given linear temporal logic formula and a product automaton of the system model. Then it searches for an acceptable trace on this product automaton lazily. Thus, the problem of verifying a linear time property is converted into the problem of invariance validation, which makes it possible to search the acceptable state by reachability analysis. Experiment results show that this lazy slicing based algorithm not only makes lazy slicing be able to verify linear time property, but also remarkably improves the scalability of LTL model checking.
状态空间爆炸问题是使用模型检测技术验证软件系统正确性面临的主要挑战之一。程序切片[1]是一种缓解状态空间爆炸问题的有效方法, 在软件模型检测技术中有着成功地应用[2, 3, 4, 5, 6]。然而, 传统的静态程序切片技术不能保证总是获得状态空间得到有效缩减的切片模型, 原因是使用静态切片方法获得的切片模型的规模除了受切片标准影响外, 还取决于系统中变量间的依赖程度。变量间的相互依赖程度越高, 静态切片方法对状态空间的压缩能力就越差。
为了解决这个问题, 研究人员在静态切片方法中引入了反例引导的抽象细化[7](Counter example guided abstract refinement, CEGAR)技术。增量式切片技术[8]和逐步回归式切片技术[9]就是这类方法的典型代表。但是这类方法在每次细化迭代过程中都要以更高的精度对全部状态空间进行搜索, 这会导致在细化前已经验证过的部分状态空间上的重复计算。文献[10]和文献[11]提出的惰性切片方法使用懒惰抽象[12]思想对基于CEGAR的切片方法进行了优化。它们能够在发现伪反例时仅细化和验证未被处理的部分切片模型, 从而消除了基于CEGAR的切片方法中的重复计算, 提高了对状态空间的压缩能力和能够验证的系统规模。
惰性切片本质上是在过近似切片上通过可达性分析搜索错误状态的过程, 这使其能够验证的性质类型局限于命题逻辑公式描述的不变性性质。从而导致惰性切片算法无法直接判定给定系统是否是某个LTL公式表达的线性时间性质, 原因是线性时态逻辑(Linear temporal logic, LTL)公式中还包含一些涉及时态的特殊算子, 如下一步“ X” 和直到“ U” 算子。为了使惰性切片能够对表达能力更强的LTL公式进行验证, 本文提出一种基于惰性切片的LTL性质验证方法。其基本思想为:构造所期望LTL性质的否定Bü chi自动机, 计算该自动机与给定模型的乘积自动机; 然后在乘积自动机上展开惰性搜索, 从而把LTL模型检测问题转换为通过可达性分析搜索可接受状态的不变性检测过程, 搜索的结果可直接转换为LTL模型检测的结果。
本文使用文献[11]和[13]中的方法给出程序等相关定义:令 
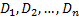

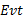
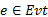
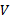
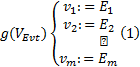
式中: 
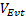
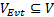
式(1)中箭头右边为一组指派表达式, 其中 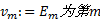

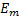
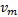
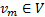

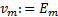
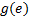

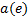
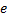
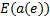

定义1 Kripke模型是一个五元组 
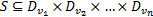
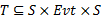
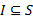

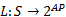
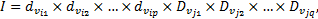
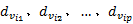
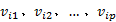
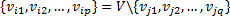
定义2 状态序列 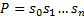

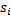
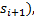
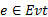
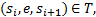
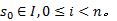
定义3 令 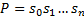
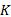
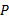
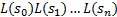
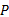
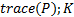
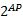
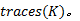
给定系统模型 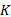
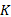
定义4 非确定性Bü chi自动机(Nondetermistic Bü chi automata, NBA)是一个五元组 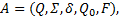
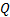
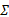
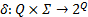
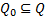
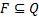
令 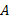
定义5 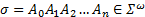

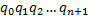

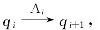
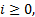

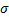
定义6 如果 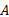
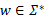
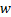
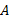
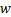

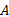
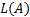
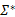
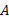
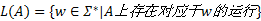
使用惰性切片算法验证LTL性质的核心步骤是把Kripke模型上的LTL性质验证问题转换为 




定义7 令 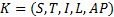

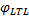
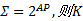


式中: 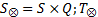
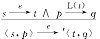
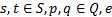
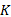
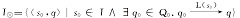

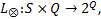
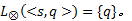
注意到 
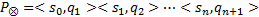
为 
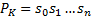
是 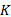
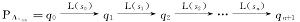
是 

被 
构造出 

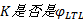





表示 



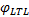
应用惰性切片算法对 

定义8 


令 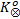




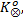
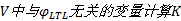
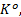
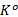

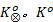
步骤1 计算 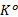
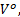

当在迭代计算过程中第一次出现 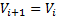
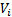
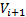
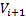
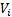
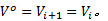
步骤2 计算 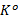
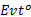
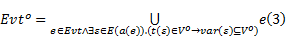
步骤3 根据 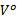
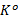

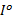
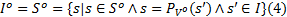
式中: 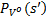

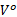
步骤1~3从 

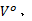
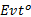
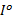
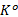
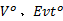
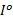

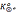
步骤4 构造 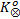
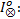
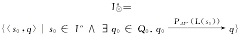
步骤5 根据 
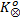
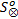

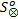

定义9 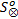
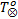
(1) 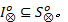
(2)对任意 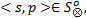
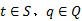


(3)有限次使用条件(1)和(2)直到 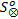
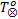
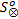
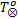
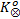
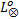
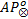
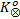


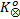


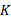
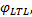
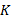
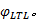
下面使用文献[10]中的进程互斥模型介绍如何计算 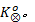
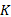

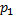
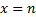
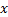

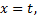
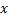
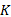




图1中被有尾无头箭头标记的状态为初始状态, 如 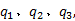
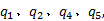


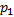
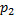

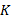
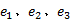
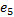
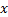
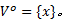

根据步骤4、步骤5可得 
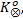
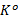
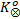
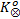
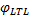

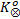
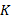
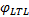
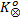

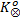
由于 
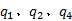

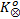
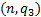

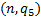




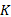

算法1给出了基于惰性切片的LTL性质验证算法 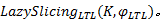
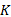
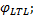


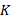
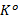

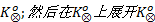
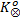
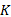
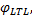
算法 1 LazySlicingLTL(K, φ LTL)
Require:Kripke model K, LTL formula φ LTL
Ensure: return true if K|=φ LTL, otherwise return false plus a counterexample
1.Compute 
2.Compute Ko according to C=(I, var(F));
3.Get 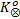

4.Let 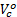
5.While flag∧ 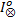
6. Get a state s from 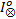
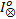
7. Push(s, U);
8. R:=R∪ {s};
9. Repeat
10. s':=top(U);
11. If s|≠ F then
12. If U is an real counterexample then
13. flag:=true;
14. Else
15. Refine 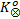
16. End If
17. Else
18. Search the successor of s' lazily;
19. End If
20. Until flag∨ U=null
21.End while
22.If flag then
23. Return true;
24.Else
25. Return Reverse(U);
26.End If
LazySlicingLTL(K, φ LTL)通过把LTL性质验证过程转换为乘积自动机上的惰性搜索过程, 使惰性切片算法能够对LTL性质进行分析验证。由于这种基于惰性切片的LTL验证方法构造的乘积自动机本质上就是一种过近似切片, 所以在乘积自动机上展开的惰性搜索过程就是惰性切片过程。所以由文献[10]中对惰性切片算法的部分正确性定理和可终止性定理可得LazySlicingLTL(K, φ LTL)的部分正确性定理和可终止性定理。
定理1 令 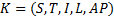
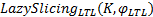
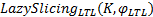

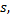
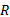


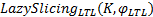
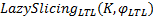
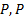

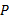

定理2 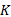
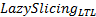
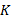
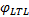
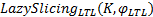
定理1、定理2保证了 
由于 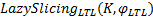







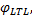
定理3 
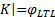
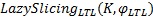
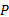
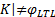
证明 令 
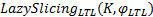
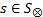

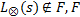


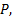


成立, 也即 

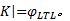
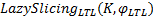
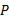
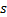
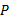

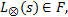



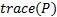

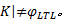
为了验证 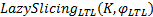
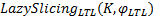

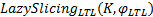
第一组实验对医保联网审计系统的支付和结算环节的部分安全性性质进行了验证, 这些安全性性质全部为LTL性质。表1列出了对基本LTL验证算法(记为BC)和 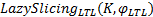
| 表1 第一组实验结果 Table 1 Experimental results of group 1 |
表1中的SatNum列表示调用可满足性判定程序的数, Cost1~Cost3分别表示三次实验过程中的验证代价, 单位为ms, Avg为Cost1~Cost3的平均时间, 单位为ms。最后一列表示模型是否满足给定性质, 如果满足结果为true, 否则为false。第二组实验在Bridge Puzzle模型上进行, 表2列出了实验结果。
| 表2 第二组实验结果 Table 2 Experimental results of group 2 |
表1、表2的实验结果说明LS算法和BC算法的验证结果是相同的, 也就是说实验结果确认了LS算法的正确性。在相同条件下, LS算法所需的判定器调用次数显著小于BC算法。主要原因是惰性切片算法保持和利用了细化迭代前的已有验证结果, 不会在每次细化过程中都对已经证明过的部分状态空间进行重复验证, 从而显著降低了SAT判定器的调用次数。
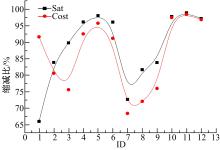
图4描述了LS算法的时间代价和SAT判定器调用次数之间的关系。其中实心矩形表示SAT判定器调用次数缩减比, 即BC与LS的SAT调用次数差与BC的SAT调用次数的比值; 实心圆点表示BC与LS验证相同性质时的时间差与BC所需时间的比值。从图4可以看出, LS时间性能的提升程度与判定器调用次数缩减比例的变化趋势基本一致。总的来说, LS算法能够在不损失验证结果正确性的前提下显著地对状态空间进行压缩。
惰性切片能够有效缓解状态空间爆炸问题, 但其仅能直接验证命题逻辑公式表达的不变性性质。本文通过把LTL模型检测问题转换为通过可达性分析搜索可接受状态的不变性验证问题, 解决了惰性切片不能够直接验证线性时间性质的问题。同时, 借助惰性切片对状态空间的压缩能力, 使得基于惰性切片的线性时间验证算法在不损失验证结果正确性的前提下能够处理更大规模的系统。进一步工作将重点研究把基于惰性切片的线性时间性质验证算法集成到SPIN中的方法, 进一步提升LTL模型检测器的可扩展性。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|



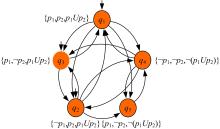
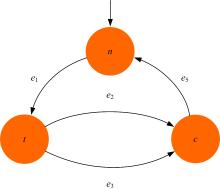
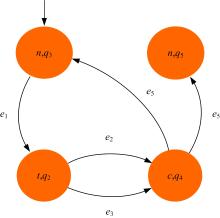
 的状态迁移系统
的状态迁移系统