作者简介:刘磊(1960-),男,教授,博士生导师.研究方向:程序设计语言及实现技术、语义网和Web服务.E-mail:liulei@jlu.edu.cn
针对已有求解多等级服务部署问题的算法存在的不足,提出了一种求解该问题的多目标遗传算法(SMOGA),建立了求解该问题的多目标优化模型。通过将个体的支配强度和被支配强度结合到一起建立对个体的评价策略,并根据评价结果进行环境选择及生成个体的交叉概率。此外还设计了一种局部搜索策略并将其融入到变异策略中,以提高变异操作的有效性。最后对SMOGA算法进行了分析,并将该算法与最近提出的求解该问题的E3-MOGA算法及NSGA-II算法在不同规模的测试用例上进行了实验对比,结果表明算法SMOGA能够更加有效地解决该问题。
The service deployment with multi-service level agreement is a basic problem to be solved for the service based software system. To overcome the shortcomings of the existing algorithms, a multi-objective model for this problem is built and a Simulation-based Multi-Objective Genetic Optimization Algorithm (SMOGA) is proposed. According to the characteristics of this problem, the genetic operations are redefined, including the introduction of individual domination strength into the environment selection, and the redefinition of crossover strategy and individual mutation strategy incorporated with local search. The performance of the proposed SMOGA was analyzed and compared with that of recently proposed algorithms E3-MOGA and NSGA-II for this problem on different scale test cases. Experiment results show that the proposed SMOGA can solve this problem more effectively.
多等级服务部署问题是面向服务的体系结构(SOA)中的一个关键问题[1, 2], 对其进行研究具有重要意义。在SOA中, 每个应用程序由一个服务集合和一个流程组成。每个服务为应用程序的功能组件, 流程定义了它们之间的相互作用。当应用程序运行时, 它的流程被实例化, 即为流程中每个服务部署一个或多个服务实例。每个服务实例服从一个特定的部署计划, 即不同的服务实例具有不同的QoS属性水平。当一个应用程序打算为不同用户分类提供服务时, 它被实例化为多个流程实例, 每个流程实例为一个指定的用户类提供一个特定的QoS属性水平。在SOA中, 服务等级协议被定义为一个实例化流程端到端的QoS属性需求, 如throughput, latency, cost。为了让应用程序满足给定的服务等级协议, 开发者需要优化服务实例组合, 即哪些服务实例用于部署哪些服务, 每个服务需要使用多少个服务实例。这种为了满足一定SLA等级, 查找每个服务和它的服务实例间的最优绑定关系的组合优化问题被称为多等级服务部署问题。
目前多数与该问题的相关研究都集中在单目标的服务选取问题上, 并利用计算代价较大的线性规划方法进行求解[3, 4]。为了降低计算代价, 近期出现了很多启发式算法[5, 6, 7], 但都只考虑单个服务等级, 并未考虑多个服务等级的情况。直到2012年Wada[8]等才开始同时考虑多个服务等级的服务部署问题, 将该问题转化为多目标优化问题, 并提出求解该问题E3-MOGA算法和NSGA-II算法。但这两种算法中每个个体没有明确的适应度函数值, 在交叉变异时个体选择是随机进行的, 这使得某些劣质个体被多次选择; 在环境选择的非支配排序过程中, 只考虑了个体支配其他个体的强度, 没有考虑个体被支配的强度。从而使得这两个算法收敛速度慢, 易陷入局部最优。此外, 由于遗传算法中变异后得到的解的质量通常不高, 在环境选择阶段很容易被过滤掉。针对以上问题, 在本文提出的多目标遗传算法SMOGA中, 对遗传操作进行了重新定义, 在环境选择过程中引入了个体被支配强度, 并设计了基于概率的交叉策略及结合局部搜索的个体变异策略, 通过将个体的支配强度和被支配强度结合到一起建立对个体的评价策略, 并根据评价结果进行环境选择及生成个体的交叉概率。最后, 通过实验对SMOGA算法进行了分析并对其有效性进行了验证。
多等级服务部署问题是一个查找抽象服务与可用具体服务之间最优绑定的组合优化问题, 是一个NP难问题, 该问题的详细定义请参考文献[8]。图1为问题的模型, 包括抽象服务流、抽象服务所对应的具体服务以及实例流程。假设存在三类用户分类:白金卡用户类, 金卡用户类和银卡用户类, 并且每个用户分类都有自己的服务等级协议。则多等级服务部署问题的解由满足三类用户等级约束的3个服务组合构成。与文献[8]中相同, 本文算法SMOGA的优化目标就是找到满足三类约束条件的解, 并且优化以下十个目标函数:白金卡用户服务组合的throughput, latency, cost, 金卡用户服务组合的throughput, latency, cost, 银卡用户服务组合的throughput, latency, cost, 以及这三个服务组合总的cost值。
针对多等级服务部署问题的特征, 首先给出个体的编码, 并给出所设计的交叉及变异操作, 然后给出个体的评价策略, 并在此基础上实现群体的环境选择及交叉概率的计算, 最后对算法进行描述及分析。
与E3-MOGA算法[8]相同, SMOGA中的每个个体代表三类用户分类的服务组合, 并且将每个个体解码为一个基因组, 图2给出了一个个体基因的实例。个体中每个基因解码为具体服务实例的数量, 该个体对应的抽象流程包含了4个抽象服务, 每个抽象服务有3个具体服务用于实现(每个服务组合有4× 3=12个基因), 并且它代表白金卡、金卡和银卡三类用户的服务组合(12× 3=36个基因)。
由个体的基因组表示可知, 每个基因代表其所关联的具体服务实例的数量, 对于与抽象服务关联的一组具体服务实例的数量, SMOGA中将其定义为与抽象服务关联的候选服务, 具体定义如下:
定义1 候选服务:在每个个体的基因组中, 将与某个抽象服务的所有具体服务关联, 并且不全为0的基因片段, 定义为与该抽象服务关联的候选服务。
SMOGA中的交叉操作将采用以候选服务组合为单位的两点交叉操作。如图3所示, 虚线将个体分解为候选服务的组合, 并且这些分界点将成为个体交叉点。图中个体 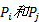
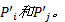
SMOGA中所采用的变异操作将首先选定个体中的一个候选服务, 然后改变候选服务中的某个基因, 被改变基因的个体为变异操作产生的个体。每个候选服务以 
为了保证变异的有效性, 将其与本文设计的一种局部搜索过程IPLS相结合, 用于变异操作后对产生的子代个体进行性能的提升, IPLS过程定义如下。
Algorithm IPLS
input:chromosome s;
output:chromosome s';
begin
s'=s;
for each a'∈ N(s) do //Neighborhood exploration
if(a' 
end if
end for
end
IPLS由两个比较重要的部分组成, 邻域探索以及接受条件。当一个个体在其邻域内探索到一个新个体解, 仅当新个体不被原个体支配且满足效用值小于原个体时才被接受。而对于个体 
定义2 邻域:对于给定的邻域规模 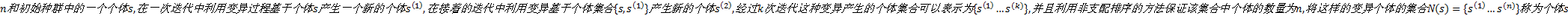
在该策略中, 同时考虑了一个个体支配其他个体和被其他个体支配的情况。给定当前的个体集 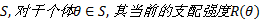

显然, 一个个体的 

式中: 
基于以上定义, 个体 

SMOGA中使用轮盘赌的方法来实现对群体中的个体的优胜劣汰操作, 从父代中以效用值的比例作为概率, 选取一些个体遗传到下一代群体。由个体 
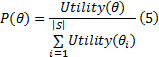
将集合中的所有个体按照效用值的大小排列, 在每次选择中, 产生一个[0, 1]的随机数, 作为选择指针来确定被选个体。
基于以上的表示, 给出SMOGA的描述如下:
算法SMOGA
g← 0
P0← randomly generated μ individuals
repeat until g == gmax {
Qk← ⌀
div=CalculateDiversity(Pg)
for each particle i in Pg{
//parent selection via Roulette Wheel
Pa(g)← RWSelection(Pg)
Pb(g)← RWSelection(Pg)
//Reproduction via two-point crossover
q1(g), q2(g)← Crossover(Pa(g), Pb(g))
//Mutation on reproduced offspring
q1(g)← Mutation (q1(g))
q1 (g)← IPLS (q1(g))
add q1 (g) to Qg if Qg does not contain q1 (g)
q2(g)← Mutation (q2(g))
q2 (g)← IPLS (q2(g))
add q2 (g) to Qg if Qg does not contain q2 (g)
}
AssignUtilityValues(Pg∪ Qg)
Gbestk+1← Top μ of Pg∪ Qg
g← g+1
}
为验证算法的有效性, 将本文算法在3个不同规模的测试用例上进行了测试, 并讨论了参数群体规模pop_size和变异概率α 对算法SMOGA的影响, 最后将本文算法SMOGA与最近提出的E3-MOGA算法[8]及NSGA-II算法[9]进行了对比分析。实验过程中根据目标函数值的变化情况和hyper-volume指标[10]对各算法的求解质量进行评价。所有算法用C语言实现, 电脑硬件配置为core(TM)2, 2.00 GHz, 3 GB RAM。
实验采用了文献[8]中两种不同的抽象流程结构, 对应3个不同的Case, 对于每个Case, 算法SMOGA运行得到的解集与算法NSGA-II、E3-MOGA运行得到的解集进行比较。由于所有对比算法具有相同的复杂度, 所以将适应度函数评价次数作为终止条件, 将它设置为Level* Length* 104, 其中Level为每个个体所表示的服务组合的等级个数, Length为个体包含的抽象服务的个数。
第一个流程包括4个抽象服务, 与case1相对应, 结构如图1所示。每个抽象服务与3个QoS级别不同具体服务相关联, 所有具体服务的QoS属性变化服从某种分布概率。case1的SLA等级约束包括白金卡和金卡用户对throughput和latency的最低约束, 银卡用户对throughput和cost的最低约束, 以及对三类用户总cost的最低约束。根据case1的抽象流程结构, 将case1的目标和属性聚合公式结合得到case1的各目标函数, 将三类用户的约束条件和属性聚合公式结合得到case 1的约束条件。依据终止条件设置, 将case1的适应度函数评价次数设置为1.2× 105, 所有结果都为10次独立运行的均值。
第二个流程为多个抽象服务的顺序流程结构, 与case2和case3相对应, case2流程结构为10顺序连接的抽象服务, case3流程结构为15个顺序连接的抽象服务。每个抽象服务与3个具体服务相关联, 所有具体服务属性值都是确定的, 即QoS属性没有按概率分布, 所有抽象服务都与这些具体服务相关联。依据终止条件设置, 将case2和case3的适应度函数评价次数设置为3.0× 106和4.5× 106, 所有结果都为10次独立运行的均值。
假设每个具体服务最多部署10个服务实例, 则一个用户分类的服务组合的搜索空间复杂度为 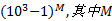




SMOGA中的主要参数包括群体规模pop_size和变异概率a。如果不考虑算法的复杂度, pop_size对算法效果的影响是显著的, 当群体规模过大时, 不易收敛, 反而影响求解的效果, 实验将群体规模的取值范围设定为从50到200以25为增量的7个值。变异概率 
为研究参数的影响, 分别在3.1小节中设置的2个不同的数据集和3个不同的case上对这些参数进行实验测试。由于不同case所得解集的hyper-volume值的数量级别不同, 将它按如下的公式进行转换:
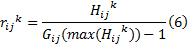
式中: 

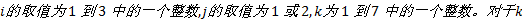


针对多等级服务部署问题, 将算法SMOGA与近期提出的E3-MOGA(多目标遗传算法)和NSGA-II(快速非支配排序遗传算法)在3个不同流程结构的case上进行实验, 这些算法的参数和终止条件为3.2小节所设定。实验将所有算法实验所得解集的hyper-volume值进行比较。表1给出了每个算法在所有case上运行得到20个结果的最大hyper-volume值, 最小hyper-volume值, 均值和变异系数(CV%)。变异系数是一种相对变异的度量, 等于标准差除以均值; 变异系数小则说明所有运行结果的hyper-volume分布较为均匀, 偏差较小, 变异系数较大则说明hyper-volume值之间差别较大。从表1可知, 用算法SMOGA求得解集的最大hyper-volume值、最小hyper-volume值和均值都比算法E3-MOGA、算法NSGA-II的相应值大, 而且在所有算法中变异系数(CV%)最小, 因此认为算法SMOGA比算法E3-MOGA和算法NSGA-II更稳定有效。而且它的有效性在图5中得到进一步的证明, 图5中明确显示了每个case上所有算法的hyper-volume值分布图。它给出了每种算法的hyper-volume值分布, 包括最小观察值、低四分位值、中位值、高四分位值和最大观察值。与E3-MOGA和NSGA-II相比, 算法SMOGA为个体设置的效用值函数更能有效地找出个体之间的细微差别, 区分个体的质量, 过滤质量低劣的个体, 保留效用值高的个体进入下一次迭代。而且算法SMOGA中的变异策略, 每次对个体进行微小的改变, 防止因为变化太大将好的解遗漏, 同时结合局部搜索中的领域概念, 使得变异效果不理想的个体有机会经过多次变异得到效果优异的解。
| 表1 不同算法Hyper-volume值对比[最大/最小/均值/(变异系数)] Table 1 Hyper-volume obtained by compared algorithms[max/min/ave(cv%)] |
 | 图5 Hyper-volume值分布图Fig.5 Statistical results of hyper-volume of compared algorithms on different cases |
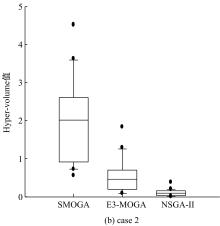 | 图5 Hyper-volume值分布图Fig.5 Statistical results of hyper-volume of compared algorithms on different cases |
针对多等级服务部署问题, 本文提出了多目标遗传算法(SMOGA)。根据该问题的特征, 在环境选择过程中引入了个体被支配强度, 对效用函数进行重新定义, 并设计了基于概率的交叉策略及结合局部搜索的个体变异策略。与算法E3-MOGA相比, 算法SMOGA中的效用函数提高了区分个体效用的精度, 防止因为算法E3-MOGA中效用相同但存在差别的优良个体被淘汰, 当这种个体为不可行解时算法SMOGA可以加速可行解的查找, 当这种个体为可行解时算法SMOGA能提高解集的优化效果。算法SMOGA结合IPSL局部搜索的变异操作, 使得个体有多次变异的机会, 能有效降低一开始变异效果不好但后期变异为高质量的个体被过滤的可能性, 从而提高算法的优化效果。最后, 将该算法在不同规模的实例上进行测试, 并且与算法E3-MOGA、NSGA-II进行对比, 结果表明本文算法在所求解集质量方面更高。此外, 用粒子群算法、遗传算法解决这个问题都没有考虑分支的抽象流程结构, 并且它们也不能很好地处理分支结构, 因此如何解决该问题是我们下一步的研究目标。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|








