轨迹(Trajectory)是空间位置随时间连续变化的时空映射, 通常使用由间隔取样点构成的序列来表示轨迹。若移动对象在

热点路径可以表示为在一段时间内移动对象频繁经过的路段, 通常它具有以下属性:①方向:即它应有起始点、终止点; ②距离:热点路径应具有一定的长度, 且应尽量保持长度的最大化; ③热度:即路径权重, 用以标识某路径上轨迹的频繁程度。

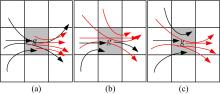
本文定义的热点路径不再是路段, 而是网格序列, 从宏观层面上看这种序列可以理解为粗粒度的路径。这样的路径表达依然面临几种难以处理的耦合现象, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 热点路径间三种耦合关系Fig.1 Three coupling relations between hot routes

(1)分裂:如图1(a)所示, 大量轨迹从 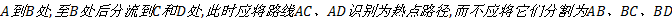三个较短的热点路径, 这样不合理的分割会使热点路径失去原有的整体性。

(2)汇聚:如图1(b)所示, 与分裂的情况类似, 这时也不应将

(3)重叠:如图1(c)所示, 路线 单独识别为热点路径。

文献[9]提出的FlowScan算法很好地解决了在路网条件下的热点路径耦合问题, 本文接下来将在无路网支持的条件下使用基于网格聚类的算法解决如上三类问题。

聚类是根据距离或密度等条件将属于同一类别的对象聚为一类, 将不同类别的对象划分开, 同一类簇内对象的相似性要尽可能大, 不同类簇内对象的相似性要尽可能小。本文提出的聚类算法与通常的概念有所区别, 其特殊性在于:

(1)类簇中的基本对象是网格单元, 有别于通常意义上的点。

(2)每个类簇实为一个网格序列, 序列中的前后邻居在地理区域上也是邻接区域, 每个类簇就对应于一条热点路径。

(3)对象间的相似性依据是“ 直接密度可达” (在3.1节中给出定义), 而不是时空距离。

定义1 区域网格划分:给定一地理区域, 将其表达为二维空间 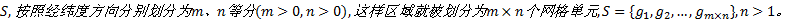将有邻边或对角相邻的网格定义为网格的近邻。将网格沿着经纬度渐增方向从1开始编号, 每个网格单元就有了唯一标识。

定义2 轨迹的网格序列:一条轨迹所经过的网格单元的序列。

定义3 网格的流量: 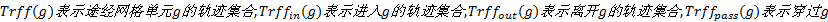的轨迹集合, 于是 的流量。

定义4 直接密度可达:网格单元 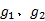是邻接单元, 如果 是预定义的最小密度可达阈值。

定义5 网格生成图:若将每个网格单元视作一个顶点, 则直接密度可达的网格单元可使用有向边表示, 网格单元间的共同轨迹数量即为有向边的权重。这样所有网格区域便可映射为一个图

定义6 路径密度可达:对于一条网格单元链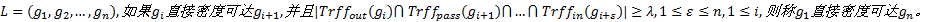

定义6中的 可视作滑动窗口的宽度, 当其取最小值1时, 只需保证链内前后相邻的两个网格满足密度可达条件即可, 但这样可能会将过多网格链接成一条热点路径, 这有违常理, 称其为弱热点路径; 而当其取最大值 时, 即要求不少于λ 个的移动对象同时经过链内的所有区域, 这样的要求过高, 不符合实际情况, 称其为强热点路径; 当 取中间值时较为合理, 这样更符合现实中热点路径的情况。比如网格区域 识别为一条热点路径, 如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 热点路径中轨迹的不同起始点Fig.2 Different starting positions of trajectories in hot route

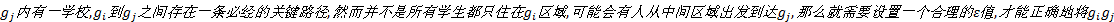
要找到所有热点路径需要两个步骤:①找到所有热点路径的起始区域; ②利用聚类方法从热点路径起始区域开始搜索, 将属于同一热点路径的所有网格区域都聚到一起。

2.2.1 热点路径起始区域

在以下三种情况下一个网格区域可能会成为热点路径的开始:

(1)如图3(a)所示, 当从区域 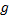出发的轨迹数量达到一定阈值时, 无论从邻接区域进入此区域的轨迹数量为多少, 此区域都可能成为热点路径起始区域。

(2)如图3(b)所示, 当 的每个邻接区域进入 的轨迹量都达不到阈值, 但从所有邻接区域汇集到区域 的轨迹总和能达到阈值时, 也可能成为热点路径的开始。

(3)如图3(c)所示, 当前两种情况都不满足, 而进入 的轨迹量与从 出发的轨迹量之和达到阈值时, 则 也可能成为热点路径的开始。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 热点路径起始区域的三种情况, λ =4Fig.3 Three kinds of start area of hot route

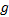
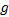
考虑上述三种情况, 可以给出热点路径起始区域的概念。

定义7 热点路径起始区域:给定最小密度可达阈值 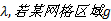满足以下三种条件之一, 则称其为热点路径起始区域:

(1) 其中网格区域 是 的邻接区域。

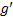
(2) 其中网格区域 是 的邻接区域, 且不能直接密度可达

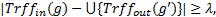
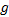
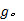
(3) 其中网格区域 是 的邻接区域, 且不能直接密度可达

那么, 是不是所有热点路径都开始于热点路径起始区域呢?下面针对这个问题给出结论和证明。

引理1 所有热点路径都是开始于热点路径起始区域。

证明 对于第一种情况, 只要从区域 出发的轨迹量超过一定量, 那么 就一定成为热点路径的开始。对于第二种情况, 用反证法, 设 是 的邻接区域, 且 直接密度可达 , 那么从 到 的轨迹量一定达到了阈值, 这样 就一定先于 成为了热点路径起始区域, 这与定义相违背。第三种情况与第二种情况类似, 不再赘述。所以, 所有热点路径都一定开始于热点路径起始区域。

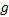
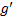
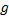
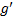
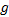
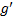
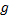
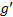
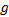
2.2.2 聚类过程

使用定义7的规则依次判断所有网格单元就能找到所有热点路径起始区域, 然后利用定义6的规则从每个起始区域开始聚类搜索, 判断滑动窗口内的网格区域是否直接密度可达, 若是, 则加入聚类; 若不是, 则停止迭代, 完成聚类。这样便能找到所有热点路径。那么, 如何在众多的网格单元中有效地完成聚类搜索呢?不失一般性, 假设每个热点路径起始区域都有多个密度可达的邻接区域, 且其每个邻接区域同时有多个密度可达的二级邻接区域, 那么从热点路径起始区域开始的搜索空间可以构造成以起始区域为根节点的4叉树(每个网格单元最多有4个邻接单元), 这样网格生成图就简化为多个4叉树。显然, 使用深度优先搜索算法对树的每个分支逐个搜索就能找到所有以根节点起始的热点路径。在搜索某个分支时每向下递进一级, 就使用定义6判断滑动窗口内的网格是否满足条件, 若满足则将当前节点对应的网格区域加入热点路径中, 若不满足则终止当前分支的搜索, 完成一条热点路径, 然后开始搜索下一个分支, 直至所有分支搜索完毕。

2.2.3 本文算法

总结以上过程, 可给出热点路径探测算法如下:

算法1 GridGrowth

输入:网格矩阵M, 轨迹数据集合T, 轨迹量阈值λ , 窗口宽度ε

输出:热点路径集合R

Hot_Route_Set GridGrowth(Matrix M, Trj_Set T, Min_Traffic λ , Win_Width ε ){

1.初始化R为空集;

2.将M转换为网格生成图G;

3.找到所有热点路径起始区域S;

4.foreach(Hot_Route_Start_Area s in S){

5. r=new Hot_Route();

6. SearchHotRoute(s, r, R);

7.}

8.Return R;

}

void SearchHotRoute (Hot_Route_Start_Area s, Hot_Route r, Hot_Route_Set R){

1.N=s的直接密度可达的邻接区域集合;

2. if(N!=null){

3. foreach(Neighbor_Grid n in N){

4. if(路径密度可达条件能够满足){//滑动窗口重叠邻接区域n, 按照定义6判断

5. r’ =Copy(r); //生成r的副本

6. r’ .Add(n); //将当前区域追加到路径末尾

7. Search_Hot_Route(n, r’ , R);

8. }

9. else

10. R.Add(r); //完成当前分支的搜索, 将找到的热点路径加入到集合中

11. }

12. }

13. else

14. R.Add(r); //当前网格单元没有直接密度可达的邻接区域, 完成此次迭代

}

为了证明本文算法所找到的, 热点路径是完备的, 给出如下引理及证明。

引理2 给定 值, 则GridGrowth算法所找到的热点路径集合是完备的。

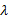
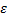
证明 只要给定直接密度可达阈值λ , 那么依照定义7找到的热点路径起始区域的集合一定是完备的。这是因为热点路径起始区域是严格依照定义7逐个网格查找的, 不存在某个网格单元被遗漏或不满足定义的条件却又是起始区域的情况。又因为在给定 时每个网格单元的直接密度可达的邻接单元是确定不变的, 那么以热点路径起始区域为根节点的4叉生成树也是确定不变的。随之, 在给定窗宽 时, 按照定义6所获得的序列也是确定不变的, 即验证所找到的热点路径集合是完备的。

实验中所用的数据是深圳市2011-04-18~2011-04-26期间的出租车GPS轨迹数据, 车辆总数为13 798台, 记录的采集间隔不恒定(间隔≥ 30 s)。数据格式如下:

name:车牌号;

time:采集时间点;

jd:经度;

wd:纬度;

status:车辆状态(0=非打表, 即空载; 1=已打表, 即重载);

v:车速(单位为:km/h);

angle:行车方向(0=东; 1=东南; 2=南; 3=西南; 4=西; 5=西北; 6=北; 7=东北)。

轨迹的划分以车辆的状态变化(status值)为依据, 当status值由0变为1时表明有乘客开始乘车, 当status由1变为0时表明乘客下车, 这时认为车辆完成了一次有意义的轨迹。这样的轨迹记录了人们的实际出行行为, 那么利用这些轨迹所挖掘出的热点路径能真正揭示人们的移动规律。

实验中所研究的目标区域只取深圳市的某一核心区域(113.79≤ jd≤ 114.18; 22.46≤ wd≤ 22.7), GPS数据也取自这个范围内。经统计这一区域白天的轨迹量在13 500条/h左右。图4显示的是此区域内1 h内的轨迹分布状况。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 轨迹分布图(红色为轨迹, 灰色为路网)Fig.4 Taxi traces in Shenzhen City

算法中共有4个参数:最小密度可达阈值

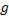
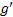
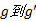
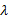
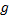
对于λ , 可以设置为固定值, 比如30/h。从常识可以判断, 若一个网格 到邻接网格 的单向车流量能超过每小时30辆, 就可认为从 的路径比较“ 热” , 即从 是直接密度可达的。这里注意, 实际交通量会远远大于这个数字, 之所以设置的低是因为实验数据只是一部分出租车轨迹, 并不包含其他类型车辆的大量轨迹。然而, 因为各个城市的交通状况不同, 一个城市不同区域的交通状况也不相同, 所以将 设置为固定值就容易忽略掉区域间的不同之处。若 值设置太大, 低流量区域的热点路径会被遗漏; 若 值设置太小, 高流量区域中就可能会识别出大量的伪热点路径。为避免以上问题可以将 设置为相对值, 如 但这样会存在另一种问题, 比如从 达到最大值, 但不能认为从 到 可以成为热点路径。所以, 基于以上两方面考虑, 将λ 设置为两个值, 即固定值λ _const和相对值λ _ratio, 这样同时满足两种条件才能确定从 密度可达。

对于ε , 则跟网格单元大小有关。若网格很小, 比如长、宽均为100 m, 而一条路径的长度可能要超过1000 m才能将它视为热点路径, 那么 就需要设置为较大值, 比如10; 若网格很大, 比如长或宽均为500 m, 那么ε =3就比较合适。

网格大小与研究区域的总面积大小和算法效率等因素有关。一般认为, 一个网格的长或宽在300~600 m比较合适。至于 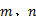的大小会不会对算法的结果有很大影响, 将在下一节进行讨论。

实验中将根据不同的参数值对算法结果做几组对比:首先对比不同 值的结果, 此时所用的数据为2011-04-18日07∶ 00∶ 00~08∶ 00∶ 00的数据, 各参数取λ _const=25, λ _ratio=0.8, m=100, n=50。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同ε 值时的热点路径数量统计Fig.5 Statistics of hot routes for different ε values

图5是 时, 所找到的都是“ 强热点路径” , 即每条路径中都有一定量的轨迹跨越这条路径的所有网格, 但这样只能找到最短的热点路径, 而遗漏很多长路径。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同ε 值时的热点路径探测结果Fig.6 Detected hot routes by GridGrowth algorithm for different ε values

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同ε 值时的热点路径探测结果Fig.6 Detected hot routes by GridGrowth algorithm for different ε values

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同ε 值时的热点路径探测结果Fig.6 Detected hot routes by GridGrowth algorithm for different ε values

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同ε 值时的热点路径探测结果Fig.6 Detected hot routes by GridGrowth algorithm for different ε values

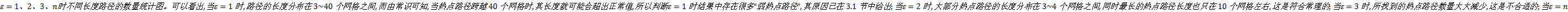
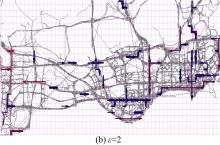
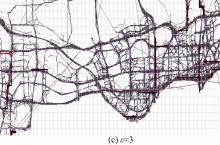
图6是 ε取以上值时的热点路径探测结果, 其中灰色曲线表示车辆轨迹, 彩色线段代表热点路径, 箭头表示路径方向, 线段越宽表示路径“ 热度” 越高, 颜色越红表示路径长度越长。从图中可以更清晰地看出ε =1时存在一些过长的“ 弱热点路径” , ε =2时识别的路径则分布比较均匀, ε =3时只识别出了很少的一部分短路径, 而ε =n时某些长路径被不合理地分割或截断了。

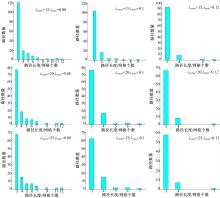
图7为对比不同λ 值时的结果, 取ε =2, m=100, n=50。观察图7可知, λ _const与λ _ratio值都会影响结果, 当λ _const取较小值时(如λ _const=15)会识别出大量短路径, 而当λ _ratio取较大值时(如λ _ratio=0.12)只会识别出极少的长路径。由图7还可以观察出, 当λ _const由小变大时各类型路径的数量并没有太大变化, 而当λ _ratio值由小变大时所识别出的长路径数量大幅下降, 由此可见实验结果对λ _ratio值更敏感。实验表明, 当λ _const=20~25, λ _ratio=0.08~0.1时结果更符合实际情况, 当然这只是针对1 h的数据量而言, 它们的值应根据数据量的大小适当调整。限于篇幅这里不再讨论如何根据数据量来调整两个值的大小。

图8为不同网格数量对结果的影响, 此时取ε =2, λ _const=25, λ _ratio=0.08。由图8观察可知, 当网格数量为80× 40时所得的长路径数量最多, 随着网格数量的增加所得的长路径数量逐渐减少。这是因为随着网格变小, 邻接网格间的共同轨迹数量会变少, 这样就会造成很多邻接网格无法密度可达。这时若要保持三种情况下的结果相差不大, 就需对ε 和λ 的值进行调整。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 不同λ 值时的热点路径数量统计Fig.7 Statistics of hot routes for different λ values

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 不同网格数量时的热点路径数量统计Fig.8 Statistics of hot routes for different grid numbers

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 两种算法的热点路径探测结果对比Fig.9 Comparison of detected hot routes by GridGrowth and TraClus

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 两种算法的热点路径探测结果对比Fig.9 Comparison of detected hot routes by GridGrowth and TraClus

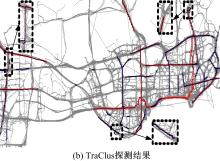
这里与经典轨迹聚类算法TraClus^[5]进行对比, 如图9所示。

观察图9(a)可发现, 凡是轨迹密集的地方所识别出的热点路径也较多, 且所识别出的热点路径长度分布均匀, 这是符合实际情况的。观察图9(b)中的 区域可发现, GridGrowth算法能够准确识别出热点路径的复杂耦合现象, 即出现热点路径分裂、汇聚、重叠等情况时仍能很好地将它们区分开。其中 区域对应于重叠现象。

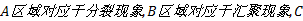
图9(b)显示的是TraClus算法所获得聚类的代表性轨迹(Representative trajectory), 由图可知该算法能够将具有相似性的轨迹聚类到一起, 能一定程度地表达轨迹的运动趋势, 但由于算法只考虑轨迹的相似性、不考虑路径间的轨迹连通性而导致聚类结果中存在一些超长聚类(> 8 km), 这种情况下的聚类结果就不能表示热点路径了。而且, TraClus算法也不能有效识别热点路径的耦合现象(对比图9(a)(b)中的 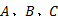区域)。

通过以上对比可以看出, GridGrowth算法比TraClus算法能够更有效地识别热点路径。

本算法主要包括以下三个阶段:

(1)数据预处理:即将轨迹转化为网格序列, 这一过程主要是将各个GPS轨迹点分配到相应网格中, 每处理一个点需要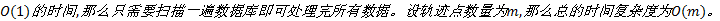

(2)探测热点路径起始区域:这一过程只需逐一探测每个网格单元的邻接单元即可。若网格数量为

(3)聚类:此阶段是要生成所有热点路径, 这一过程的时间复杂度跟热点路径起始区域的个数、路径长度、滑动窗口宽度以及网格单元内的车流量有关。假设起始区域的个数为