作者简介:代劲(1978-),男,副教授,博士.研究方向:智能信息处理,灰理论.E-mail:daijin@cqupt.edu.cn
从灰关联分析中最核心的灰关联度构造及相应的挖掘算法出发,结合正态分布的普适性,提出了一种体现数据分布特点的正态灰数,并给出了相应的灰度及灰关联度计算方法。在此基础上,构建了一种多粒度无监督的快速灰聚类方法,无需先验知识即可完成自动聚类。通过实验验证了本文方法的有效性,为大数据下灰关联分析的进一步发展提供了新思路。
The classic grey theory does not adequately take into account the distribution of data set, and lacks effective methods to analyze and mine large sample in multi-granularity. Considering the universality of normal distribution, a normality grey number is proposed. Moreover, the corresponding definition and calculation method of the incidence degree between the normality grey numbers are constructed. On this basis, the grey incidence analysis method in multi-granularity is put forward to realize the automatic clustering in the specified granularity without any experience knowledge. Experiments fully demonstrate that the proposed method is effective in knowledge acquisition for large data.
灰色系统理论[1]是以“ 部分信息已知, 部分信息未知” 的数据为研究对象, 通过对“ 部分” 已知信息的生成、开发, 提取有价值信息的不确定性知识获取模式[2]。
灰关联分析是灰色系统理论的重要组成部分, 根据各因素之间发展趋势的相似或相异程度来衡量彼此接近程度。灰关联分析不仅是灰理论的重要研究内容, 同时也是灰色系统分析、预测和决策的基石。目前, 众多学者对此进行了深入研究, 取得了较多的研究成果。针对二元组及语言学习中的多属性群决策问题, 文献[3]提出了基于不完全权重信息的灰关联分析方法; 文献[4]根据指标权重的重要性进行灰关联分析, 解决了股票投资中的多标准决策问题; 针对多属性决策中属性权重的模糊问题, 文献[5]提出了相应的灰关联分析解决方案; 文献[6]用数据的凸性表征样本之间的相似程度, 提出了三维灰色凸关联度的概念; 文献[7]提出了一种基于灰色关联分析和D-S证据理论的决策方法, 显著降低决策的不确定性; 文献[8]将模糊集理论中MYCIN不确定因子和灰色关联方法相结合, 建立推理决策模型; 文献[9]将某一对象属于或不属于某一类别的不确定性程度视为灰度, 提出一种面向集合论的灰度定义与灰数分级方法; 文献[10]提出了方案量变和质变的判定方法和评价者判断质量变化的测度指标, 从而建立了基于灰色关联度的时间权重确定模型。
从以上研究成果可知, 灰关联分析领域正朝着针对数据分布本身, 以降低数据的不确定性方向发展。同时, 更加注重与其他不确定性知识获取方法的相互借鉴, 互相补充。但当前的灰理论研究中, 还缺乏针对数据分布的灰关联分析研究。在信息处理越来越朝大数据、大样本方向发展的当今社会, 越来越凸显出该需求的紧迫性。大数据下灰关联分析的核心在于建立具有较强数据表示能力, 同时便于进行高效数据处理的信息粒子。本文结合数据自身的概率分布, 提出了正态灰数概念并给出了相应的灰度及灰关联度。在此基础上, 构建了一种多粒度的快速无监督灰聚类方法, 无需先验知识即可完成自动聚类分析。在仿真实验中, 该方法取得了较好的效果, 为大数据下灰理论的进一步发展提供了新的思路。
灰数是已知大概范围而不知其确切数值的数。它是灰色系统的基本单元。
定义1 灰数[1]:指在某一个区间或某个一般的数集内取值不确定的数, 通常用 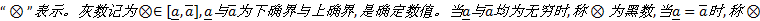
灰数可以通过人们对它的认识加以白化。通常, 借助白化权函数[1]来描述对一个灰数在其取值范围内不同数值的“ 偏爱” 程度。灰色白化权函数反映了人们在主观上掌握的该灰数的信息, 而灰数的灰度则是对该灰数的灰程度的测定, 反映其信息量大小。邓聚龙[1]给出了典型白化权函数灰数灰度:
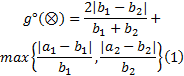
基于灰区间长度 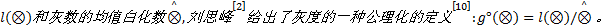
以上给出的灰度定义皆存在当灰区间长度 
灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法, 其基本思想是通过灰色关联度来比较参考数据列和若干个比较数据列的几何形状相似程度。灰关联度越大, 则序列间发展方向和速率越接近, 关系越紧密。灰色关联分析方法要求样本容量可以少到4个, 对无规律数据同样适用, 不会出现量化结果与定性分析结果不符的情况。
按照相似性度量原理的不同, 目前灰关联度可分为3类:基于距离的方法、基于斜率的方法和基于面积的方法。其中, 邓氏灰关联度和广义灰关联度是应用较为广泛的两种灰关联度计算模型。
定义2 邓氏灰关联度[1]:设 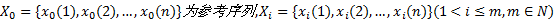
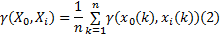
式中: 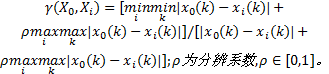
邓氏灰关联度满足灰关联四公理, 两级最大差与最小差充分利用了多个比较序列的信息, 分辨系数的选择能够削弱比较序列中异常值对关联空间的影响, 使关联度更好地体现出系统的整体性。
广义灰关联度分为灰色绝对关联度和灰色相对关联度, 这两种算法的区别在于通过不同的数据变换方法, 分别从相似性和接近性两个角度衡量数据序列。灰色绝对关联度采用的是始点零化算子, 而灰色相对关联度采用的是初值化算子。
定义3 广义灰色关联度[11]:设序列 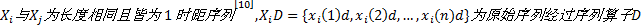
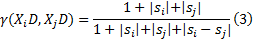
式中:|s|=| 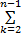

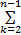
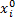
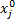

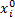
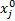
灰色绝对关联度采用两曲线间相交面积的大小作为序列相似性的度量标准。曲线越相似, 始点零化像越接近, 从而相交面积越小, 关联度越大。
灰色关联度是灰色关联分析的基础, 然而无论是邓氏灰色关联度还是广义灰色关联度, 均对区间序列数据的分布特征考虑不足。当序列本身满足一定的统计特征时, 通过简单的极值或折线段面积计算将具有比较大的误差, 直接影响到关联度取值。
如果某一现象决定于若干独立的、微小的随机因素的总和, 并且各个因素的单独作用相对均匀地小, 那么这一现象一般近似于正态分布。
定义4 正态灰数:指在某一个区间或某个一般的数集内取值不确定的数, 且该数的取值满足区间内均值为 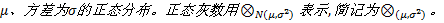
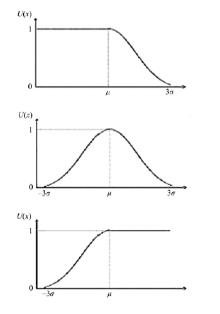
借助正态灰数定义, 可以给出正态灰数的典型白化权函数, 如图1所示。
正态灰数具有普遍意义, 由Lindeberg-Levy中心极限定理, 任意一个概率分布中生成的随机变量, 在序列和(或者等价的求算术平均)的操作之下, 均会统一规约到正态分布, 即: 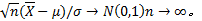
根据正态分布的性质, 正态灰数具有以下的一些性质:
(1)给定 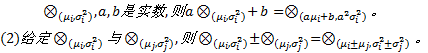
正态分布中, 随机变量的取值具有一个明显的特征, 即在 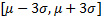
定义5 正态灰数灰度:设 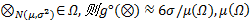
在此定义下, 可以得到正态分布灰数的形式化描述: 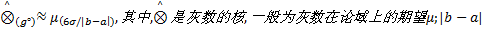
基于正态分布的灰度为灰理论在大数据下进行多粒度知识获取提供了一种新的思路。但需要特别注意的是, 虽然正态分布具有良好的普适性, 但实际中也存在许多不符合正态假设的数据分布, 如数学中常见 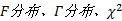
对于非正态数据, 可以先将非正态分布数据进行正态化转换再进行估计, 如Box和Cox提出的幂转换方法[15]、Johnson分布曲线族方法[16, 17]。也可以采用Bootstrap再抽样法[18]进行处理。以研究样本做为抽样总体, 从研究样本中反复抽取一定数量(如抽取500次)的样本, 通过平均每次抽样得到的参数作为最后的估计结果。
灰色绝对关联度是灰色关联分析的基础, 然而邓氏灰关联度和广义灰关联度均存在以下问题:①序列 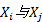
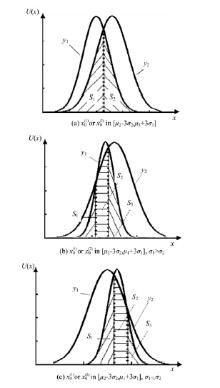
基于以上分析, 结合正态灰数性质, 本文提出一种基于正态灰数的灰关联度, 该关联度以正态随机分布为核心, 通过计算两个正态分布相交面积得到关联度。两个正态分布之间的相交情况如图2所示, 阴影部分面积反映了彼此的相似情况。
设 
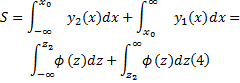
式中: 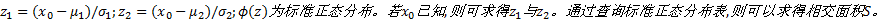
由两分布曲线相交, 故 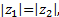
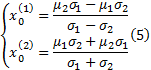
由正态分布的3σ 规则可知, 有99.74%的数值落在区间 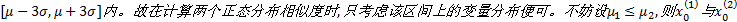
(1) 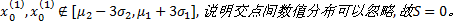
(2)若存在 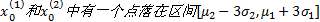
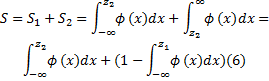
式中: 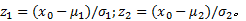
(3)若 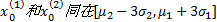
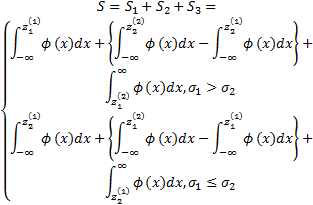
式中: 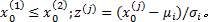
考虑到相似度的规范性, 需对 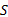
定义6 正态灰数关联度:给定正态灰数 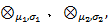
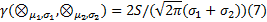
式中: 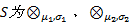
正态灰数关联度简称正态灰关联度。正态灰数关联度更好地考虑了数据在区间内的变化情况, 体现了其概率分布特性, 为基于正态灰数的灰关联分析打下了坚实基础。
灰色聚类是灰关联分析的核心内容, 通过灰数关联矩阵或灰数的白化权函数将观测指标或观测对象划分成若干个可定义类别。目前, 灰色聚类仅支持小样本数据, 而且聚类过程需要人工进行参与, 增加了算法的复杂性与不确定性。基于此分析, 本文提出了一种多粒度无监督快速灰色聚类算法。算法以正态灰关联度为核心, 通过构建灰关联矩阵, 采用改进的k-means方法实现无监督动态聚类。
k-means是一种效率较高的动态聚类算法, 然而传统k-means算法存在着需要人工指定聚类个数, 容易陷入局部最优解的缺陷。基于此, 本文对k-means算法进行了改进。
算法基于如下分析:在聚类时, 将特征最为相似的样本数据划分在同一类中, 而它们在空间中的相互关系可以按照某些范数度量的大小关系来表征。通过逐步增加层数(即聚类数), 层间类与类相互关系随着层数的增加不断变化, 可以某种准则来刻画这种变化, 一旦达到要求, 即表示聚类完成。本文用样本标准差 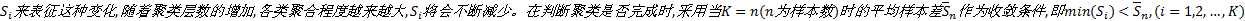
基于正态灰关联矩阵, 可构建基于灰关联度的无监督快速灰色聚类算法。
算法1 基于正态灰关联度的无监督快速灰聚类
输入:给定序列
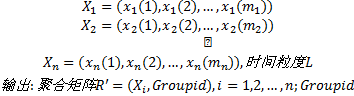
算法步骤:
(1)计算序列初值像与始点零化像//排除序列数据量纲不一致、初始值不一致带来的影响。
(2)对序列进行时间粒度为 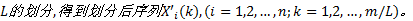
(3)对序列进行正态分布假设检测。若不满足, 则进行正态分布转换。
(4)对 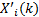
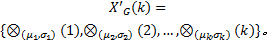
(5)计算正态灰序列 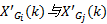
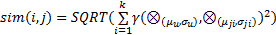
得到正态灰关联矩阵 
(6)提取 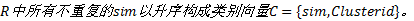
(7)计算阈值 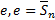
(8)初始类别K=1, v=0//v为循环控制变量。
(9)Do
①构建中心类别表 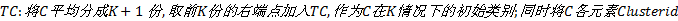
②设定临时循环控制变量 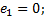
③当 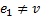
a) 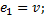
b)计算 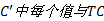
c)根据加权平均修正TC中各类别的中心距离;
d)计算 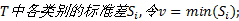
④ 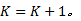
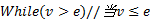
(10)根据C中sim, 对应更新R中Clusterid。
(11)设置 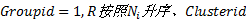
①依次取 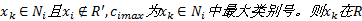
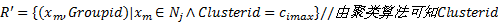
② 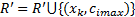
③ 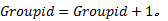
(12)返回 
经过算法1聚类处理, 得到序列在灰关联度下的等价簇, 相同 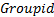
算法1采用正态灰关联度作为序列相似度计算基础, 对序列的长度、序列取值都无严格要求, 适用于大样本、多粒度的灰关联分析。
为了考察算法的性能, 采用UCI数据库中的“ Individual household electric power consumption” 数据集进行仿真测试。该数据集记录了一个家庭4年的用电量情况(间隔一分钟采样, 时间从2006年10月至2010年11月), 有效记录数据2 049 280条。
根据数据集特点, 需要按年分析数据集的用电情况, 以月为分析单位找出每年的用电高峰、低谷。
采用算法1对数据集进行处理, 首先得到时间序列在指定时间粒度(月份)的正态灰序列, 如表1所示。
| 表1 数据集1转换后的正态灰序列 Table 1 Converted normal grey sequence of dataset |
按年份对正态灰序列进行指定粒度(月份)聚类, 得到如下聚类结果(按照期望降序排序):

可看到, 在2007-2010年期间, 耗电情况最多的发生在1、2、11、12月, 而且呈稳步递增状态; 3、4、5、6、9、10月耗电量较多, 变化较为稳定; 用电量最小的月份为7、8月, 而且耗电量波动情况最为明显。以2009年每月耗电量为例, 聚类结果如图3所示。
从图3中可以看出, 采用算法1进行多粒度聚类处理后的结果与实际数据分布情况较为相符, 整个过程无需人工参与或经验知识, 计算结果体现出了数据的概率分布特性, 充分证明了算法的正确性。
虽然灰理论正日渐成熟, 但实际应用还不够广泛。一个重要原因是灰理论缺乏行之有效的针对大数据集及多粒度的灰关联分析方法。本文在考虑数据概率分布的基础上, 建立了正态灰数概念并完成了相应的灰度定义。在此基础上, 提出了基于正态灰关联度的多粒度灰关联分析方法。整个分析方法无需先验知识即可完成自动聚类分析, 在聚类实验中取得了较好的效果。在后续的研究中, 将展开正态灰序列的GM模拟及预测模型研究, 建立完整的正态灰关联分析、多粒度模拟与预测理论体系。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|