作者简介:周相超(1987-),男,博士研究生.研究方向:同步算法,信道编码与调制.E-mail:zhouxiangchao@hrbeu.edu.cn
针对连续相位调制(CPM)信号载波相位同步困难的问题,提出一种通用的CPM信号的载波相位软同步算法。在CPM调制信号的Rimoldi分解的基础上,基于最大似然准则和EM算法推导了载波相位的软同步算法,该算法将解调器与同步器联合,利用CPM软解调器输出的软信息进行载波相位估计。仿真结果表明,该算法能够得到接近修正克拉美罗限的载波相位估计,并获得近似理想的误码率性能。
Considering the difficulty of phase synchronization for Continuous Phase Modulated (CPM) signals, a general Soft Carrier Phase Synchronization (SCPS) algorithm for different signals is proposed. Using Rimoldi decomposition of CPM signals, the SCPS algorithm is derived based on maximum likelihood criterion and the Expectation-Maximization (EM) algorithm. The synchronizer and demodulator are iterated jointly. The soft demodulation information provided by CPM soft demodulator is used to aid the carrier phase estimation. Simulation results indicate that the Root Mean Square Estimation Error (RMSEE) of the SCPS algorithm is very close to that of the Modified Cramer-Rao Bound (MCRB) for general CPM signals, and the bit error rate could achieve approximate ideal performance.
连续相位调制(CPM)是一类先进的调制技术, 具有相位连续、频谱特性优良的特点, 与PSK调制相比, 具有更高效的频带利用率和功率利用率, 而且调制之后的信号包络恒定, 对功率放大器的非线性特性不敏感, 非常适合于信道传输。目前, CPM的两种特例MSK和GMSK已广泛应用于卫星通信、深空通信和以GSM为代表的数字蜂窝移动通信等领域, 但因接收机复杂度较高、信号同步存在较大困难, 通用的CPM尚未获得广泛的应用[1]。
目前, CPM信号的载波同步方法主要分为数据辅助同步和非数据辅助同步[2]。数据辅助同步方法的同步性能较好, 但需占用额外的传输带宽和功率; 非数据辅助同步方法不需额外的带宽和功率, 但同步精度较差, 且仅适用于信噪比较高的情况, 很难实现有效同步。
近年来, 随着具有接近香农限的高性能的Turbo码和LDPC码的广泛应用, 逐渐兴起了一类新的“ 码辅助同步” 算法。码辅助同步算法基于最大似然准则, 将译码器与同步器进行联合迭代, 从而获得接近理想的载波同步性能。文献[3]将Turbo码译码结构与最大似然准则结合, 基于期望最大算法与和积算法进行迭代载波同步, 可以获得较精确的同步; 文献[4]提出了基于译码软信息的改进的极性判决相位检测算法, 在低信噪比条件下可获得较传统方法更理想的同步性能; 文献[5]通过将锁相环与LDPC译码器结合, 使用迭代译码过程中的外信息来获得接近理想的相位估计; 文献[6]提出一种基于译码软信息反馈的载波同步算法, 不需导频序列即可获得载波相位的最佳估计值; 文献[7]基于最大似然准则, 提出简化的导频联合编码辅助载波同步算法, 该算法能大幅提高同步参数的估计精度和范围, 在一定的导频长度下可逼近理想同步; 文献[8]中针对SCCPM串行级联系统, 提出一种Turbo同步结构, 通过CPM信号的正交指数分解和卡尔曼滤波来估计载波相位; 文献[9]针对LDPC-CPM迭代系统, 提出一种最大化后验概率均值的载波同步算法。
由Rimoldi分解可知:CPM信号可以分解为连续相位编码器CPE和无记忆调制器MM的组合[10], 因此CPM信号具有类似于卷积码的网格记忆结构。本文在Rimoldi分解的基础上, 借鉴Turbo码和LDPC码的“ 码辅助同步” 思想, 提出一种通用的CPM信号载波相位同步算法。该算法基于最大似然准则, 分别使用MAP算法和EM算法对CPM信号进行解调和相位估计, 将解调器和同步器联合设计, 利用解调器输出的软信息辅助载波相位的同步。
CPM信号具有相位连续、包络恒定的特点, 其复指数形式的表达式为[11]:
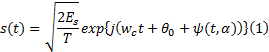
式中: 


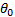
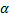
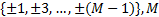

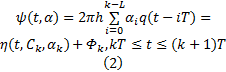
式中: 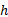
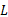
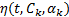
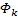
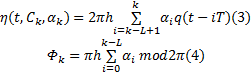
式中:向量 
CPM信号的相位响应函数 
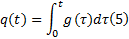
具有以下特性:

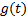
传统的CPM信号使用Viterbi算法实现相干解调, 不便于软信息的提取, 为此, 采用MAP算法对CPM信号进行软解调, 以获取载波相位同步所需的软解调信息。
由Rimoldi分解可知, CPM信号隐含一个具有记忆性的网格编码器, 类比卷积码的网格图, 可定义 


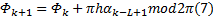
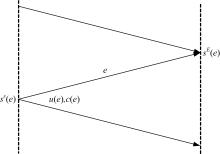
CPM信号的网格图如图1所示, 其中 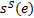


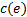


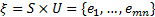
根据MAP算法的原理:若网格状态图已知, 则输出码字概率、输入比特概率、状态转移概率等多种概率分布均是可计算的, 根据码辅助同步思想, 在推导CPM信号的载波相位同步算法的过程中, 可由MAP算法计算所需的解调软信息类型。
本文给出的算法和仿真都是基于图2的系统模型的。系统采用Rimoldi分解的方式产生CPM信号, 解调为基于MAP算法的软解调方式, 传输信道为高斯白噪声信道(AWGN), 其双边功率谱密度为 
CPM信号 

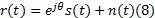
式中: 
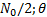
依据贝叶斯理论, 载波相位的最大似然估计值 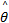
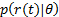

在CPM信号的最大似然检测中, 匹配滤波器用于产生软解调的先验信息, 输出度量定义为:
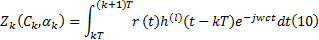
式中: 

相位分支 

表示网格图中一条可能的传输路径。在CPM信号的网格图中, 从一个节点 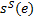
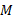
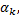
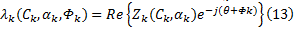
因此, 载波相位 

由最大似然准则, 为估计载波相位, 需要对式(14)求导, 令导数为零, 得到载波相位的最大似然估计值, 但方程没有闭环解, 数学求解困难, 因此需要使用其他方法来近似, 传统方法有数据辅助和非数据辅助的近似方法[13], 本文使用EM算法, 采用迭代方式逐步接近载波相位的最大似然估计。
EM算法是一种广泛应用于参数估计领域的迭代求解算法, 适用于存在隐含变量的优化问题, 算法的目标是找出包含隐性变量的概率模型的最大可能的解[14]。EM算法包括E步骤和M步骤, 经过E步骤和M步骤的多次迭代, 可获得未知参数的近似最大似然估计值。
在E步骤中构造 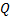

M步骤用于获取新的估计值:

式中: 
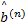
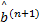

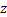

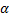

接收信号的表达式如式(8)所示, 载波相位 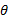
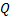
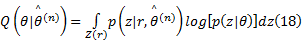
由式(17)可将后验概率 
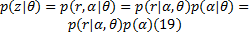
将式(17)和式(19)带入式(18)可得:

式中:最后一个等号右边第二项与相位 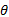
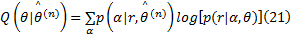
式中: 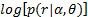

因传输信道为AWGN信道, 似然函数 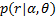
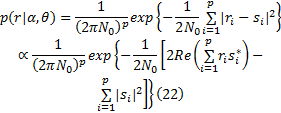
因此 

对于 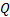
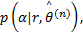
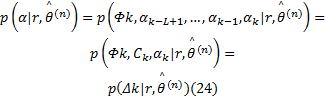
式中: 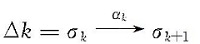
综合式(23)的对数似然函数和式(24)的后验概率表达式, CPM信号载波相位 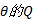
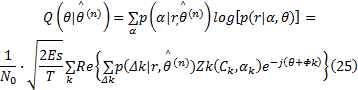
因此, 基于EM算法对CPM信号的载波相位进行估计时需要2种信息, 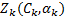
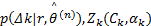

由EM算法原理, 在获得 
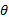
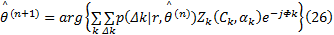
至此, 推导出了基于EM算法和CPM软解调的载波相位软同步算法, 该算法利用解调器输出的状态转移信息来辅助载波相位估计, 以迭代的方式获得接近最大似然的载波相位同步, 既避免了最大似然估计求解困难的问题, 又可获得较高的估计质量。
基于图2所示的系统模型对本文提出的CPM信号的载波相位软同步算法进行性能仿真, 仿真参数设置如下。采用的CPM信号类型为:进制数 
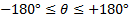
图3给出了载波相位估计的均方误差曲线, 作为对比, 同时给出修正克拉美罗限(MCRB)、传统的数据辅助估计(DA)的均方误差曲线, 其中, 载波相位的修正克拉美罗限为[15]:
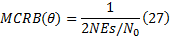
由图3可以看出, 当Eb/N0≥ 5 dB时, 载波相位软同步算法的均方误差估计性能逐渐接近MCRB, 与传统的DA方法性能相近。
图4给出了在多种相偏、不同信噪比条件下CPM信号的误码率性能, 由图4可见, 当Eb/N0≥ 5 dB时, 载波同步逐渐趋于收敛, 系统性能损失低于0.1 dB, 相位偏差对系统性能的影响得到抵消, 系统的误码率接近理想同步系统的性能。
图5给出了CPM信号在归一化信噪比为6 dB和8 dB条件下相位估计的范围。可以看到:相位未补偿时, 误码率受相位偏移影响较大, 使用本文算法对载波相位偏移补偿之后, 误码率性能得到改善; 该算法能有效估计的相位偏移范围是 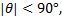
因同步困难, CPM信号的应用受到较大局限, 本文借鉴最新的码辅助同步思想, 基于最大似然准则, 将CPM信号的解调器与同步器联合, 利用解调器输出的软信息去辅助载波相位的估计, 从而达到载波相位同步的目的。当Eb/N0≥ 5 dB时, 相位估计误差接近MCRB, 系统的误码率性能损失低于0.1 dB, 可估计的相位偏移范围为 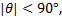
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|