作者简介:王宏志(1961-),男,教授.研究方向:数字信号处理及应用,图像处理,通信中的信号处理.E-mail:wanghongzhi@mail.ccut.edu.cn
结合维纳滤波器的光滑PL分块压缩感知恢复算法(BCS-SPL)可以去除图像分块压缩感知块效应,但是收敛速度慢,尤其是在低采样率条件下,为此将BCS-SPL算法与光滑0范数压缩感知算法(SL0)相结合提出一种基于光滑0范数分块压缩感知算法(BCS-SSL0PL)。通过对不同图像对比BCS-SPL和BCS-SSL0PL算法的恢复效果和恢复时间、信号恢复迭代次数,可以证明BCS-SSL0PL在较低采样率条件下能以较少的迭代次数,较快的恢复时间获得与BCS-SPL相当的恢复效果,而且与BCS-SPL相比,BCS-SSL0PL对不同的采样率恢复时间变化不大,方便于不同场合的应用。对比两种算法恢复图像的细节,BCS-SSL0PL算法还能改善低采样率条件下恢复图像的块效应。
The BCS-SPL algorithm, which combines the Wiener filter with PL compressive sensing signal recover algorithm, can overcome the blocking artifacts but its convergence speed is slow. To overcome the slow convergence speed of the BCS-SPL algorithm, especially on small measure rate, the BCS-SPL algorithm is combined with smooth L0 norm compressive sensing signal recovery algorithm, and a BCS-SSL0PL algorithm is proposed, which can speed up the image compressive sensing. The performance of the BCS-SSL0PL algorithm was compared with the BCS-SPL algorithm in terms of recover image quality, recover time and iteration times. Results show that the proposed BCS-SSL0PL algorithm surpasses the BCS-SPL algorithm that it can achieve the same recover quality with less time; it needs nearly the same time for different measure rate conditions; furthermore, it can improve the blocking artifacts on small measure rate conditions.
最近几年压缩感知信号处理问题得到了广泛的发展。压缩感知(Compressive sensing, CS)打破传统信号处理领域奈奎斯特采样定率[1, 2, 3]。压缩感知理论表明, 如果信号是稀疏的或者是可压缩的, 则信号能在低于奈奎斯特采样频率采样的条件下以高概率恢复出原信号。同时, 压缩感知理论框架下, 将信号采样和信号压缩两个步骤结合起来, 即信号采样之后就是压缩的信号。压缩感知算法主要包括三个方面, 信号稀疏变换、观测矩阵设计和恢复重构算法[4]。其中恢复重构算法直接关系到重构精度的大小, 运算时间的长短, 决定着CS理论是否切实可行。
传统图像压缩感知算法往往是将图像转换成一维信号, 但是图像信号转换成一维信号往往长度很大, 导致需要压缩感知的测量矩阵尺寸很大, 使得恢复过程占用巨大内存, 恢复速度缓慢。为了解决压缩感知在图像处理上的应用, L Gan[5]提出了分块压缩感知算法(Base-block CS, BCS)。BCS利用分块的思想解决图像信号占用内存巨大、恢复效果缓慢的问题。为了解决BCS算法分块带来的块效应, Fowler等[6, 7]提出一种BCS-SPL算法, 引入维纳滤波器的PL(Projected landweber, PL)算法作为信号恢复算法, 减少分块效应。但是BCS-SPL中采用的恢复算法是PL算法, 收敛速度慢, 特别是在低采样率条件下, PL算法迭代时间长, 迭代次数多, 使得维纳滤波器作用的次数多, 造成恢复图像容易模糊。为了解决BCS-SPL算法低采样率条件下恢复时间长的问题, 本文提出了一种结合光滑0范数(Smoothed L0, SL0)压缩感知恢复算法的加速分块压缩感知算法, 加快了信号收敛速度, 减少了迭代次数, 实现了算法加速。
假设原信号 
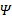

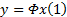
式中: 
原信号的稀疏性是压缩感知对信号的唯一要求。压缩感知信号恢复问题转换成寻找信号的一个最稀疏解问题[3]。 

但是求解最小0范数是一个NP-hard问题, 经过几年的研究, 学者提出了许多恢复算法。最著名的是基追踪算法(Basis pursuit, BP)[1]。BP算法将0范数凸优化的问题放宽到1范数, 通过1范数的凸优化问题的解代替0范数优化问题的解:

虽然BP算法恢复效果很好, 但是算法计算复杂度高, 信号恢复时间长, 因此之后又提出了许多以贪婪算法为基础的迭代算法。
图像压缩感知中, Gan[5]首先提出图像分块压缩感知BCS(Block-Base CS)。BCS主要思想是将原始图像分为较多尺寸相同的小图像块, 对这些图像块采用相同的观测矩阵, 同时, 在信号恢复端分别对这些图像块进行恢复, 组合成整幅图像。
图像 

式中: 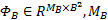
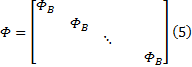
整个图像观测值 
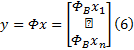
各个恢复图像块 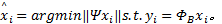
BCS算法虽然解决了图像压缩感知信号恢复占用内存巨大、恢复速度缓慢的问题, 但是由于分块操作时的恢复图像有明显的块效应。针对图像块效应, Fowler等[6]基于维纳滤波器的PL算法提出了BCS-SPL算法。
图像信号的恢复采用PL算法结合维纳滤波器对信号进行恢复, 同时去除因为分块产生的块效应。SPL算法处理过程如下[6]:
Function x(i+1)=SPL(x(i), y, Φ B, Ψ , λ )
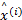
For each block j



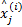

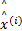

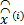
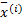
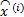
For each block j

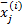
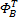

Fowler等[7]之后还结合近几年的压缩感知算法对BCS-SPL算法做了进一步的改进, 并将BCS-SPL算法推广到图像编码器的设计[8]以及视频压缩感知[9, 10]。
光滑0范数(Smoothed L0, SL0)[11, 12]是针对欠定系统 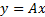
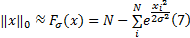
所以求信号最稀疏解转换成求解有约束最小化问题:
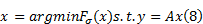
SL0算法采用最速下降法迭代求解最小化问题:

同时 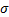
传统BCS-SPL算法虽然采用了结合维纳滤波器的PL算法作为图像重建算法。但是, 由于低采样率条件下PL算法收敛速度慢, 导致图像重建迭代次数过多, 维纳滤波器作用于图像的次数多, 使得重建的图像容易变得模糊。而SL0算法本身采用最速下降法逼近全局解, 收敛速度非常快, 重建时间短。为了减少低采样率条件下图像重建算法迭代次数, 本文结合SL0算法的优点对BCS-SPL压缩感知恢复算法进行改进。
从SPL处理过程可以看出, PL算法是对图像变换域直接做阈值收缩, 发现SL0算法也是对图像变换域进行处理, 因此先采用SL0算法的最速下降法对图像变换域进行一次最小值逼近:
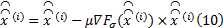
对用最速下降法逼近的最小值做阈值收缩处理:
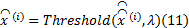
同时, 由于增加了一次最速下降法的逼近过程, 在做阈值收缩时收缩系数需要做适当的变化。SL0算法是获取图像变换域中的最稀疏解, 因此每次阈值收缩系数 

由式(12)可以看出, 当迭代获得的近似0范数逼近图像在变换域的稀疏度为 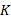

BCS-SSL0PL算法步骤如下:
Function x=BCS-SSL0PL(y, Φ B, Ψ )
ε =0.00001, max_iterate=200
σ min=0.00005, μ 0=4.3, λ 0=6, η =0.6
For each block j
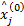

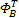

End for
e= 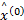
While e< ε and i< max_iterate
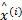
For each block j

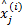
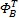
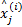
End For
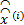
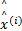



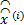
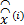
λ (i)= 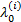
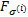
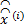
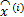
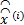
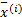
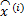
For each block j
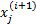
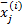


End For
e= 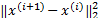
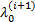
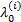
If σ (i)> σ min
σ (i+1)=γ σ (i)
Else
σ (i+1)=σ (i)
End If
End While
End Function
从上面的介绍可以看出, BCS-SSL0PL算法相对于BCS-SPL算法在于每次迭代增加一次最速下降法的最小值逼近步骤加速, 同时用逼近的近似0范数去控制收缩系数, 减少重建算法迭代次数, 加快了分块压缩感知算法重建速度。迭代次数的减少可以一定程度避免维纳滤波器的多次作用而使得图像变得模糊的问题。
选取不同的图像分别用BCS-SSL0PL算法和BCS-SPL算法对图像进行恢复。每幅图片的采样率为0.1~0.9, 每个采样率重复试验10次, 取平均值作为试验结果。图像稀疏变换选择DCT变换。试验中两种算法采用同一个采样矩阵和变换矩阵, 具体参数设置如上述BCSSL0PL算法所描述。
试验选取Lenna、Man、Peppers、Bridge四幅图像作为试验图像, 图像大小为512× 512。恢复图像信噪比如表1、表2所示。从恢复图像的信噪比可以看出, BCS-SSL0PL相对于BCS-SPL算法并没有多少提升, 效果相当。选取0.2采样率的Lenna和Peppers恢复图片对比两种算法恢复图像的局部细节, 如图1所示。可以看出, 对于Peppers图像, BCS-SSL0PL算法信噪比高于BCS-SPL算法, 且BCS-SPL算法可以明显看出块效应, 而BCS-SSL0PL算法则没有。而在Lenna图像, BCS-SSL0PL算法虽然信噪比没有BCS-SPL算法高, 但是恢复的视觉效果并不比BCS-SPL差, 同时也没有BCS-SPL算法恢复图像的块效应。
| 表1 BCS-SPL对应采样率恢复信噪比 Table 1 BCS-SPL recover image psnr for different meshement ration |
| 表2 BCS-SSL0PL对应采样率恢复信噪比 Table 2 BCS-SSL0PL recover image psnr for different meshement ration |
 | 图1 BCS-SPL与BCS-SSL0PL算法恢复细节比较Fig.1 Details comparison of recover images between BCS-SPL and BCS-SSL0PL |
两种恢复算法计算时间如图2所示。从恢复的时间可以看出, BCS-SPL算法对于不同采样率图像恢复时间有很大的变化, 但是BCS-SSL0PL算法对于不同采样率的恢复时间比较平稳, 变化不大。而且在0.1~0.5采样率条件下, BCS-SPL恢复算法都是比较长的, 基本上都在30~50 s左右, 无法应用于实时性要求高的场合。但是BCS-SSL0PL恢复算法的恢复时间远远小于BCS-SPL算法, 所有恢复时间都在12~18 s左右。
BCS-SPL算法中涉及对图像分块, 图像分块尺寸的大小对算法恢复精度、恢复速度都有影响。为了比较不同分块尺寸下两种算法的性能, 对512× 512的Lenna图像分别采用8× 8、16× 16、32× 32分块对两种算法进行测试。测试结果见表3。
从表3可以看出, 对于不同的分块尺寸, BCS-SSL0PL算法的恢复时间都比BCS-SPL算法减少30%以上。
| 表3 不同分块尺寸BCS-SPL与BCS-SSL0PL算法比较 Table 3 BCS-SPL and BCS-SSL0PL comparison with on different block size |
通过对基于光滑0范数的图像分块压缩感知算法的研究, 建立了BCS-SSL0PL的算法模型, 实现了分块压缩感知算法的加速, 同时避免了分块压缩感知算法在低采样速率情况下恢复图像的块效应, 且仍然能保证与原有BCS-SPL算法同等的恢复效果。试验过程中, 当采样率为0.1时, BCS-SSL0PL算法恢复效果不理想, 这是因为采样率过低, 计算得到的近似0范数和真实0范数有很大的误差, 最速下降法的最小值逼近陷入局部最小值。这个问题需要对不同的图像选取不同参数加以解决, 这些参数的选择也是下一步研究的问题。同时, 由于并不是所有的图像恢复效果都优于BCS-SPL算法, 所以对于BCS-SSL0PL算法的恢复精度也是下一步研究的重点。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|



