作者简介:康荣宗(1983-),男,博士研究生.研究方向:通信信号处理,压缩感知.E-mail:laok_169@163.com
针对模拟数字变换器(ADC)无杂散动态范围(Spurious free dynamic range, SFDR)性能评估受测量方法和测试参数限制,导致测量偏差较大的问题,分别从量化和采样两个角度出发,在对ADC的量化噪声谱分析的基础上,通过数学推导给出了理想的ADC在不同量化比特条件下的无杂散动态范围的理论上界。同时分析阐明了SFDR性能和输入信噪比之间的关系;并进一步分析了在不同采样频率条件下,ADC输出信号离散谱的特点及其对无杂散动态范围性能的影响,并结合傅里叶分析测试法验证了推导结果的正确性。
Spurious Free Dynamic Range (SFDR) measurement of Analog to Digital Converter (ADC) is restricted to the specified ADC parameters and matching test methods. In this paper, first, a theoretical analysis of approximate upper bound performance of ideal ADC with different quantization bits is carried out based on spectral analysis of quantization noise. Then, the relationship between the SFDR performance and the SNR of input signal under Additive White Gaussian Noise (AWGN) is illustrated. The effect of sampling on SFDR is also considered that the characteristic of discrete spectrum of ADC output and its influence on SFDR with different sampling rate is investigated. The mathematical deduction results are verified with FFT analysis test method.
无杂散动态范围(SFDR)是衡量ADC动态范围性能的重要指标。其定义是:当一个正弦信号输入到ADC时, 正弦信号的功率除以在ADC输出端信号频谱的最大寄生信号峰值功率[1]。这个指标是评价一个ADC在非常大的信号存在的情况下, 能够检测到非常小的信号的能力。在宽带接收设备中, ADC的SFDR是制约整个接收系统动态范围的关键因素, 因此对于ADC的无杂散动态范围性能参数的测试和研究很重要。
目前, 针对ADC动态范围的分析方法中, 大部分研究者主要针对实际的工程应用测试需求, 采用满幅度的正弦信号作为ADC的输入激励源, 对ADC输出的数据进行统计处理, 包括直方图统计[1]、正弦波匹配[2]、傅里叶分析[3]等, 但这些方法在具体的测试分析过程中由于受到采样样本数需求过大、测量参数较为单一、频谱泄漏和频谱混叠等因素的影响[4], 并不能得到精确的结果, 具有一定的局限性。另有一部分研究者从ADC的量化误差角度出发, 假定量化误差是在量化台阶内均匀分布且与输入信号无关的随机变量, 进一步得到ADC的无杂散动态范围为[5]:

式中: 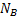
文献[6]将Dither噪声与输入信号相加后进行ADC量化, 减弱输入信号与量化噪声的相关性, 在一定程度上改善了ADC的SFDR性能, 但受Dither幅度的影响。此外, 将量化误差近似为均匀分布的假设是有一定条件的, 如文献[7]建立的量化理论认为如果输入信号的两维特征函数是带限的, 那么量化噪声就是与输入无关的白噪声, 这一条件是充分而非必要条件; 文献[8]进一步建立了充分必要条件, 认为如果输入信号的特征函数是一个 
本文从ADC的量化和采样角度出发, 首先基于ADC量化噪声谱的分析, 通过数学推导分别给出了在无噪和加性高斯白噪声条件下, 单音正弦信号激励的ADC的SFDR性能理论上界; 阐明了SFDR与输入信号的幅度、信噪比以及量化间隔等因素之间的关系; 进一步推导分析了多音正弦输入下ADC的量化噪声谱及其对SFDR性能的影响。最后, 结合傅里叶分析法, 分析了不同采样率条件下量化噪声谱的分布及其对SFDR性能的影响。
理想ADC主要包括采样和量化两个过程, 且在一般的情况下采样过程在量化过程之前, 为了分析问题的方便, 将这两个过程调换了顺序, 但并不影响分析的结果[11]。假定输入信号序列 
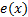
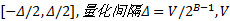
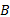
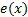
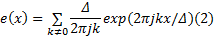
假设量化器的输入信号为:
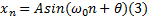
同时假设采样速率是输入正弦信号频率的整数倍。式(3)中: 
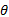

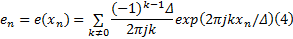
将式(1)代入式(2), 并利用如下Jacobi-Anger公式:

式中: 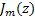
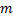

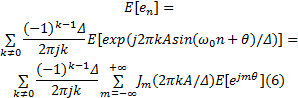
由于当 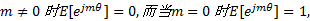

又因为 
利用上述推导方法可以进一步得到 

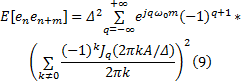
由于 

由上述推导可以看出, 正弦信号输入时的量化噪声是一个平稳随机过程, 当量化比特数增大时, 
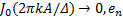

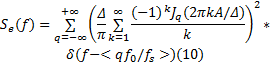
式中: 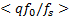
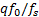
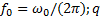
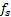
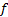
基于ADC量化过程的基本模型, 可以得到量化输出为:
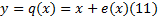
而输出的功率谱为:
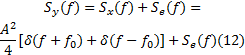
将式(10)代入到式(12), 可以得到:

通过上面的分析可知, 量化后的正弦信号的功率谱由一系列离散分量组成, 而根据双边谱和单边谱的关系, 可得到基波分量的输出幅度为:

而第 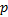
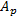
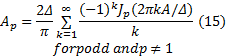
该结果与文献[14]一致, 只是推导过程和结论表达形式不同。
通过对式(14)(15)的计算和比较分析, 可以获得ADC量化输出的最大谐波分量 


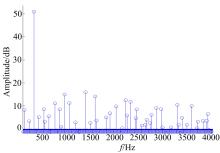
进一步利用Matlab对式(16)进行仿真分析, 图1给出了不同量化比特位数条件下的最大谐波分量位置。由于 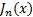
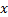
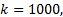

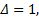

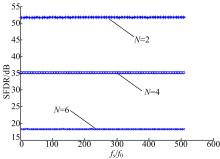
图2给出了通过式(16)并结合式(14)(15)和傅里叶分析法[13]得到的不同量化比特下ADC的SFDR性能, 可以看出理论值与仿真结果完全一致, 其中式(14)(15)的求和项数 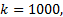
由此, 在一定量化误差范围内, 进一步利用最小二乘拟合可以得到理想ADC的SFDR性能和量化比特 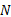
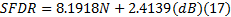
下面分析加性高斯噪声对于量化噪声谱的影响, 即假定输入信号为:
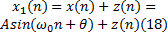
式中: 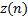
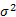
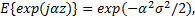
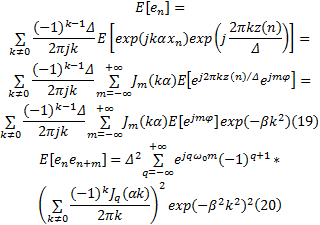
式中: 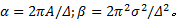
根据功率谱与自相关函数之间的傅立叶变换关系, 就可以得到量化噪声功率谱为:

因此, 加性高斯噪声条件下ADC输出的基频分量的幅值为:
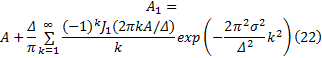
而第 

将式(22)(23)代入式(16), 可以得到高斯信噪比下的ADC的SFDR的具体表达式。图3给出了ADC的SFDR性能和 
结合上面的分析可知, 谐波分量的幅值及其ADC的SFDR性能依赖于 
下面分析多音正弦输入情况下, ADC的量化噪声谱的分布情况。首先考虑当输入为两个正弦信号的情况, 假设输入信号为:

式中: 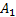
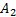


同样利用上述推导方法, 可以得到量化噪声的功率谱为:

式中: 

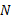
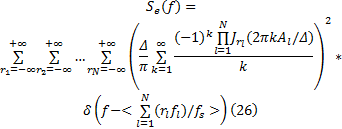
式中: 
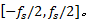
根据ADC的一般分析模型, 采样是量化之后必不可少的一个环节, 而采样后的信号以采样频率为周期在频谱上无限拓展。通过上面的分析, 可知激励信号经过ADC的量化之后, 特别是在量化比特大于3时, 其最大谐波分量的位置位于奈奎斯特区间之外, 采样率 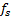
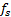
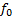
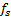
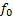
Case1 



Case2 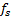
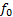

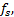
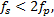
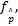

式中:Int表示将小数点后面的数字全部丢弃, 仅保留小数点之前的整数部分。
定义 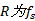




图6给出了当 

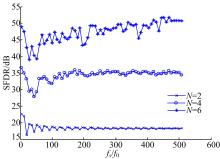
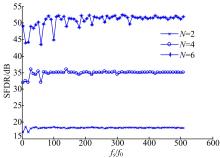
图7给出了在不同量化比特N=2、4、6的条件下, 不同采样频率的SFDR的分布情况。从图7可以看出由于欠采样引起的频谱镜像混叠作用, ADC的SFDR不再是一个恒定值。在采样率相对较低时, 在奈奎斯特频率范围内, 其镜像混叠作用明显, SFDR性能由于具体的采样倍数和谐波分量分布的影响而呈曲线变化趋势。随着采样率的不断提高, 量化噪声功率分布到更宽的频谱范围之内, 镜像混叠的作用相对减弱, 最后收敛于未考虑采样的情况。此外, 量化位数越小, 其各谐波分量的幅值越大, 但由于总的噪声能量不变, 使得谐波分量与基频分量的幅值相对差值越小, 则ADC的SFDR性能的收敛速度越快。
Case3 


式中:gcd表示最大公约数。
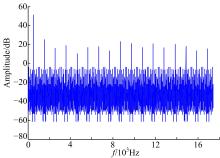
图8给出了该条件下的正弦信号输入的ADC的输出离散谱分布, 其中f0=5× 64 Hz, fs=128× 64 Hz, gcd(fs, f0)=64, 量化比特N=4。ADC量化采样后的信号重复周期为f's=128, 每个重复周期内包含了 

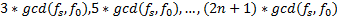
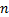
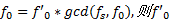
图9给出了 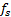
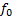
在ADC量化噪声谱分析的基础上, 首先从理论上推导给出了ADC的SFDR性能的数学表达式, 并给出了理想条件下SFDR的最小二乘拟合上界, 进一步分析了输入信号幅度、量化台阶、加性高斯白噪声、多音正弦输入等因素对其性能的影响, 为实际ADC性能的测试和系统的设计提供了理论依据。接着分析了采样因素对ADC的SFDR性能的影响, 结合Matlab仿真重点分析了采样率和输入信号频率在互为质数、具有最大公约数、整数倍等不同条件下的ADC输出离散谱和SFDR性能的变化趋势。从仿真结果及其分析可以看出, 在两个频率值互为质数时, 其SFDR性能稳定, 最有利于对ADC的SFDR性能进行测试, 而具有最大公约数下的性能好于整数倍的情况, 此外, 采样频率越大其性能越趋近于稳定值。当然, 采样频率、量化精度、输入信号幅度等因素在实际测试和应用中也受到具体器件性能和测试信号的制约, 在具体工程设计中需要综合考虑。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|