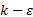作者简介:王靖宇(1976-),男,副教授,博士.研究方向:汽车空气动力学.E-mail:wangjy@jlu.edu.cn
应用计算流体力学方法,采用重叠网格的策略,对直道行驶的简化模型进行瞬态数值模拟研究,然后进行风洞试验验证。在此基础上,对弯道行驶状态下简化模型周围流场的瞬态气动特性进行了数值模拟,得到了弯道行驶状态下模型周围的流场分布和气动阻力系数等气动特性,并与直道行驶状态下的结果进行对比分析。结果表明:弯道行驶车辆受到了瞬态侧向力及横摆力矩的作用,并且随着转弯半径的减小,侧向力和横摆力矩急剧增大,行使速度的变化也会带来侧向力和横摆力矩的改变,从而影响车辆的行驶稳定性。本文为进一步研究弯道行驶车辆的瞬态气动特性提供了理论参考。
Computational Fluid Dynamics (CFD) simulation with overset grid is carried out to investigate the transient aerodynamic characteristics of the flow field around a simplified model of straight driving vehicle. Wind tunnel test is conducted to verify the CFD simulation results. Based on this, CFD simulation of the flow field around a turning vehicle is carried out. The aerodynamic drag coefficient and velocity vectors are obtained. The results are analyzed in contrast with the results of straight driving vehicle. The turning vehicle experiences a transient side force and a yawing moment, both of which sharply increase as the turning radius decreases. Both the side force and the yawing moment change with the vehicle speed, which would affect the vehicle stability. This study provides reference for further study of the transient aerodynamic characteristics of turning vehicle.
汽车在转弯行驶时, 周围的流场与直线行驶时有很大的差异, 转弯车辆会受到侧向力及横摆力矩的影响[1, 2], 因此, 采用传统的直线行驶状态下试验或模拟方法获得的气动载荷不能直接应用于弯道行驶状态下汽车的系统动力学计算和仿真, 否则将会影响计算结果的准确性。
本文采用重叠网格的方法, 在直线行驶瞬态计算结果的基础上, 对弯道行驶车辆的瞬态气动特性进行了数值模拟研究, 并讨论了弯道半径对行驶车辆气动特性的影响。本文研究结果也可为进一步的弯道会车研究提供一定的理论基础。
由于本文是研究运动物体的气动特性, 所以数值模拟中要采用动网格的方法。目前的动网格方法中, 弹簧网格法对于处理位移不大的直线运动比较适用, 而层铺滑移网格方法适用于大位移的直线运动。旋转滑移网格方法虽然可以解决一些旋转运动问题, 但要求运动区域与静止区域的网格计算域外形为圆柱域, 而且交界面边界要相对规则, 这种要求不利于解决超车或会车等复杂工况的数值模拟, 所以本文采用重叠网格方法来解决动网格的问题。
重叠网格是对任意相对位置、彼此重叠的计算域中的网格进行数值离散化处理的一种网格处理方法, 它被广泛应用于运动物体以及优化计算的研究。通常不需要对初始生成的网格进行修改, 这对标准化网格技术的应用带来了极大的方便。任何重叠网格都由包含整个计算域的主域和包含运动物体的从域组成。
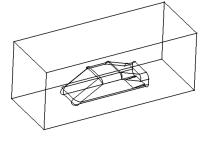
本文采用的计算模型为国际上通用的SAE阶背式1∶ 1模型, 尺寸如图1所示。SAE模型是非常简单的汽车形体模型, 仅对几个平面和棱角进行了倒角处理, 底部尾端设置有扩散器, 没有车轮和轮腔, 在汽车空气动力学的研究中获得了广泛的应用[3, 4]。
通过Catia软件建立模型, 模型的最大外边界尺寸为4200 mm× 1600 mm× 1200 mm, 离地间隙为200 mm。SAE模型周围的长方体区域为从域, 从域的外边界尺寸为8500 mm× 3250 mm× 3250 mm, 如图2所示。
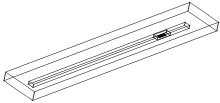
最终生成的模型如图3所示, 其中主计算域外边界尺寸为123600 mm× 24000 mm× 10500 mm, 主计算域中车辆行驶区域的尺寸为104750 mm× 3750 mm× 3750 mm, 车道前端距离入口8400 mm, 后端距离出口10450 mm, 车头距主计算域前端入口94200 mm, 车尾距主计算域后端出口25000 mm, 车尾距离计算域后端出口要有足够长的距离, 以保证车辆的尾流能够充分发展, 这样计算结果才能准确[5, 6]。
网格的划分对数值模拟的结果有较大的影响[7, 8], 本文利用STAR-CCM+进行trim网格的划分, 对于SAE模型, 底部扩散器特征线采用7.8125 mm的网格尺度, 模型其他部分的特征线使用15.625 mm的网格尺度, 模型表面最大网格尺度为31.25 mm, 边界层为10层, 生成的网格如图4所示。
从域边界处网格尺度为62.5 mm, 从域网格增长速度为8层增长一倍, 而且保证从域和主域重叠部分的网格应不少于4层。主计算域外边框采用500 mm的网格尺度, 同时将车道部分网格进行加密, 网格尺度为62.5 mm, 网格增长速度为10层增长一倍。最终生成1000万左右的网格。
主域和从域的边界条件如表1所示。
| 表1 主域和从域的边界条件 Table 1 Boundary condition of main field and secondary field |
设定从域的运动方式为直线运动:车速v=-22.22 m/s, 由车速及最小体网格尺度, 根据库朗数估算初始的时间步长为0.0002 s, 每个时间步进行5次迭代, 计算160个时间步长后改用0.002 s的时间步长进行计算。
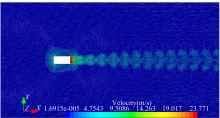
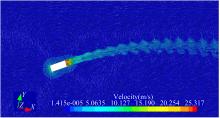
取总迭代步数后4000步的平均值做为计算结果, 得到直道行驶车辆的瞬态气动特性, 图5为某一时刻的 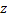
风洞试验在吉林大学汽车风洞实验室进行, 试验段尺寸为8 m× 4 m× 2.2 m, 地板为固定地板, 如图6所示。
瞬态数值模拟得到的气动阻力系数与风洞实验值非常接近, 差值在8%以内, 说明计算结果可靠性较好, 验证了瞬态直道计算方法的准确性。同时侧向力系数与横摆力矩系数都非常小, 说明车辆在直线行驶没有侧风的情况下, 侧向力和横摆力矩几乎为零, 车辆并不受侧向力和横摆力矩的影响[11]。
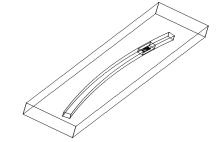
在瞬态直线行驶的基础上, 采用相同的网格设置和计算方案, 进行弯道行驶车辆的瞬态数值模拟, 研究弯道半径对行驶车辆气动特性的影响。根据国家相关法规的要求, 在满足交通安全的前提下, 弯道半径分别为400、200和100 m三种情况。弯道行驶的车辆运动方式为圆周运动, 为了保证车辆行驶时的瞬态切向速度相同, 弯道半径分别为100、200、400 m时, 车辆的行驶角速度分别为0.22、0.11、0.056 rad/s。图7为弯道半径为100 m时, 最终生成的计算域。
图8为弯道半径为100 m某时刻的 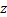
在弯道半径为100 m的情况下, 改变车辆的行驶速度, 分别模拟了速度 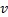
| 表2 计算结果 Table 2 Simulation results |
通过计算发现在弯道半径相同的情况下, 侧向力系数与横摆力矩系数并不会发生改变, 但侧向力和横摆力矩与速度的平方成正比, 所以侧向力和横摆力矩都急剧增大, 影响车辆的行驶稳定性。
3种不同弯道半径情况以及直线行驶工况的计算结果如表3所示, 其中CD为气动阻力系数。
| 表3 计算结果 Table 3 Simulation results |
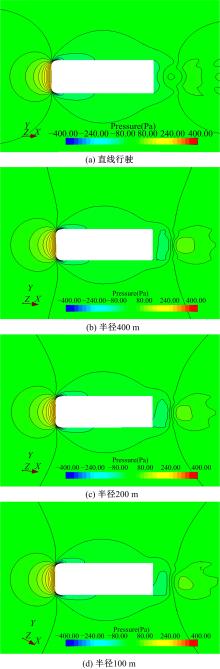
从表3可以看出, 在弯道行驶状态下, 气动阻力系数的数值几乎保持不变, 说明弯道半径对气动阻力系数并没有较大的影响。而对于侧向力系数和横摆力矩系数, 弯道行驶与直线行驶有了明显的区别。在直线行驶状态下, 两者都非常小, 几乎为零; 而在弯道行驶状态下, 侧向力系数和横摆力矩系数都明显增大, 并且随着弯道半径的减小, 弯道行驶车辆受到的侧向力也越来越大, 这会对车辆的操纵稳定性带来影响, 应该引起驾驶员的注意。如在山区公路等情况下, 弯道半径较小, 如果车速较快, 对车辆的安全行驶就会带来很大的影响, 尤其是在弯道会车的情况下, 更要考虑弯道半径及行驶速度的影响[12, 13]。
从图9(a)可以看出, 在直线行驶的情况下, 车身周围的压力分布是对称的, 所以车辆不会受到侧向力和横摆力矩的影响。当车辆转弯行驶时, 车头前部的压力在极小的瞬时并没有发生大的变化, 但左右两侧的压力不再是对称分布, 而且尾部的压力分布也发生了改变, 即使转弯半径很大的情况, 如图9(b)所示, 尾部的压力也不是对称分布, 说明车辆会受到侧向力和横摆力矩的影响。
随着转弯半径的减小, 如图9(c)(d)所示, 车辆左右两侧压力分布的不对称更加明显, 说明随着转弯半径的降低, 车辆受到的侧向力和横摆力矩会越来越大。车辆周围的压力分布变化是转弯车辆受到侧向力和横摆力矩的根源, 并导致降低车辆的行驶稳定性。
(1)弯道行驶车辆左右两侧的压力不再是对称分布, 所以会受到瞬态侧向力和横摆力矩的影响。
(2)弯道行驶车辆所受到的侧向力和横摆力矩随着转弯半径的减小而增大。
(3)在弯道半径不变的情况下, 行驶速度的增大会导致车辆受到的侧向力和横摆力矩急剧增大。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|