作者简介:杨聚芬(1988-), 女, 博士研究生.研究方向:交通信息采集、处理与应用.E-mail:yangjufenabc@126.com
为了进一步提高路网交通运行可靠性的在线分析效率,以减少信息存储空间、提高算法运行速度为切入点,借鉴图论中邻接矩阵的思想,提出了路网可靠度矩阵的概念。在此基础上,通过应用因子定理设计了路网交通运行可靠性在线分析的新方法。最后使用仿真数据对其进行了验证和对比分析。研究结果表明:本文方法在保证路网交通运行可靠性在线分析效果的同时,显著提高了运行效率,运行时间平均节省了92.72%。
In order to further improve the online analysis efficiency of traffic operating reliability of road network, a concept of reliability matrix of road network is proposed, which is based on the adjacent matrix method of graph theory. The aims to propose this reliability matrix are to reduce the information storage space and accelerate the running speed of the algorithm. On this basis, a new online analysis algorithm of traffic operating reliability is designed based on factor theorem. The algorithm is validated and comparatively analyzed using simulation data. The results show that the proposed algorithm can ensure the analysis effect of traffic operating reliability; meanwhile, it significantly reduces the running time by about 92.7% in average.
随着社会经济的发展, 汽车保有量快速增加, 导致交通事故频发、交通拥堵日益严重, 显著降低了道路交通运行的可靠性。因此, 对路网交通运行可靠性进行在线分析已成为交通系统可靠性研究领域的一个新课题。
已有的交通系统可靠性分析主要包括连通可靠性、容量可靠性和行程时间可靠性[1, 2]。由于这些可靠性分析都不能实时在线确定路网交通运行的可靠性水平, 因此, 难以满足动态交通管理的需要。
交通运行可靠性是指在规定的条件下和规定的时间内, 路段、路口或路网以规定的运行质量通过规定交通量的能力[3]。路网交通运行可靠性在线分析以动态交通数据为基础, 通过实时监测可靠度指标的变化, 在线确定路网交通运行的可靠性水平以及需要重点管理的路段和路口, 通过为动态交通管理部门提供更具有针对性的决策依据, 进一步降低路网交通运行失稳状态的发生概率、减少交通拥堵的持续时间。
文献[3]在提出交通运行可靠性概念的基础上, 构建了相应的可靠度指标, 并基于最小路集法设计了交通运行可靠性在线分析方法。该文献进一步拓展了交通系统可靠性分析的范畴, 能在线确定路网交通运行可靠性的水平及敏感的路段和路口, 有效地改善了动态交通管理决策的信息基础, 但在算法效率和时效性方面还存在较大的提升空间。
为此, 本文以文献[3]提出的交通运行可靠性概念及可靠度指标为基础, 借鉴路网结构表达的邻接矩阵思想, 构建了新的路网可靠度表达和存储方法, 并基于因子定理设计了新的路网交通运行可靠性在线分析方法。最后应用仿真试验对本文方法的效果和效率进行了对比分析。
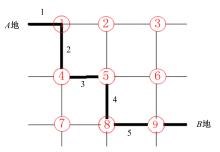
路网是由点、线相互交错组成的复杂网络, 其中, 点代表路口, 线代表路段, 如图1所示。
在图论中, 网络的表达与存储主要有邻接矩阵法、邻接表法和边集数组法。文献[3]运用邻接表法对路网进行表达和存储, 其优点是便于查找任一顶点的关联边及邻接点, 不足是由于需要与逆邻接表联合使用, 致使其占用的存储空间较大, 并导致以此为基础的路网可靠性分析计算量较大、耗时较长, 对交通运行可靠性在线分析的实时性具有不利影响。
为了减少路网存储的空间占用量以及后续的路网交通运行可靠性在线分析的计算量, 本文借鉴邻接矩阵法思想, 设计了路网可靠度矩阵的概念及其表达与存储方法。
邻接矩阵法[4]是利用二维数组 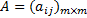
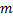


式中:当 
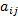
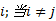



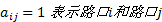


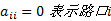
以文献[3]提出的分时可靠度指标为基础, 借鉴邻接矩阵的思想, 本文定义一种可靠度矩阵, 并将其作为路网交通运行可靠度表达与存储的新方法, 其中, 路网可靠度矩阵是指运用路口和路段的分时可靠度 
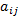

式中: 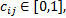
与邻接表法相比, 可靠度矩阵占用的存储空间较小, 且能够在表征路网连通性的同时体现路段和路口的分时可靠度水平, 为进一步改善路网交通运行可靠性在线分析的效率奠定了重要基础。
文献[3]将路网交通运行可靠性分析分解为特定路径的交通运行可靠性分析、特定OD对间子路网的交通运行可靠性分析和路网整体的交通运行可靠性分析三个层次。其中, 路网整体交通运行可靠性分析的基础是路网中所有OD对间子路网交通运行可靠性分析的结果。因此, 路网交通运行可靠性分析的本质是路网中任意OD对之间的端端可靠性分析。
目前交通系统中的端端可靠性分析大多采用枚举法和容斥原理法。文献[3]采用的是枚举法, 方法比较直观, 但计算量较大; 容斥原理法易于理解, 但容易导致较大的累计误差。已有研究表明[5, 6], 常应用于机械零部件可靠性分析的因子定理法可在一定程度上克服前两种方法的不足, 快速有效实现端端可靠度计算。因此, 为了改善路网交通运行可靠性在线分析的时效性, 本文在路网交通运行可靠度矩阵表达与存储的基础上, 结合路网自身特征, 引用因子定理法设计了道路网络交通运行可靠性在线分析新算法。
A.Satyanarayana和Mark K.Chang[7]最先将因子定理应用于网络的端端可靠性分析, 随后Fu-Min Yeh等[8]将因子定理应用到 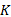
因子定理法[7]的基本思想是针对特定网络的任意节点对, 按照特定条件选择某个部件作为最优分解元, 考虑其可靠与不可靠两种状态对该节点对之间的端端可靠度矩阵进行分解降维, 反复选择最优分解元进行降维迭代, 直到将端端可靠度矩阵化简为一个由若干个二维子端端可靠度矩阵或最简子端端可靠度矩阵(不存在可行分解元)构成的多项式为止, 由此即可实现对端端可靠度进行快速估计。
对于由节点集 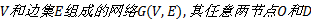
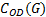
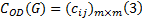
式中: 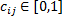
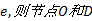
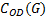

式中: 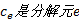
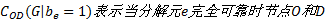
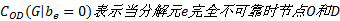
在子端端可靠度矩阵中, 对于非起始、终止节点 
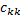
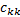

反复对各项子端端可靠度矩阵进行降维和分解处理, 直到每一个子端端可靠度矩阵为最简矩阵或者为二维矩阵, 即将端端可靠度矩阵化简为一个由二维子端端可靠度矩阵或最简子端端可靠度矩阵构成的多项式。基于此多项式, 即可按照常规方法计算出所分析 
在上述迭代分解过程中, 最优分解元是满足特定条件的可行分解元, 其选取结果对端端可靠度的估计效率具有重要影响。依据文献[5]、文献[11]和文献[12]的相关研究, 在端端可靠度矩阵或子端端可靠度矩阵中, 

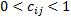
(1)对于 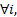
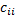
(2)对于 


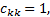
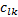
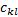
(3)对于 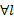
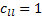


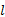
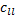
(4)当起始节点的可靠度为1时, 即端端可靠度矩阵或子端端可靠度矩阵的第一个对角元素为1时, 则该行和该列上所有非0且非1的元素所对应的部件为可行分解元。
(5)当终止节点的可靠度为1时, 即端端可靠度矩阵或子端端可靠度矩阵的最后一个对角元素为1时, 则该行和该列上所有非0且非1的元素所对应的部件为可行分解元。
对于可行分解元在可靠度矩阵中对应的元素 

式中: 
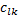
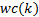

(6)取 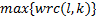

在道路交通网络中, 实际上并不存在固定的输入节点和输出节点, 出行者可以选择任何 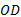



对于特定的路网, 基于因子定理的路网交通运行可靠性在线分析的基本思想是:首先任选一 
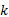
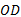
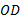


路网交通运行可靠性在线分析方法可动态追踪路网交通运行稳定性的演化过程, 实时指出路网系统的薄弱环节, 为交通管理者和出行者的动态决策提供更有利的信息支持, 有助于加快交通拥堵的疏散速度。
设路网 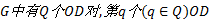
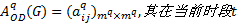
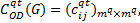
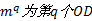

Step1 在 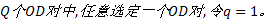
Step2 令第 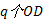
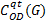
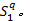
Step3 在待分解的可靠度矩阵集合 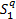

Step4 在 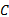
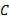
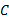
Step5 在 

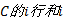

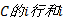


Step6 按照2.1节中的方法确定 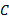
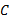
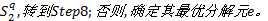
Step7 按照式(4)对 
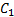
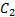
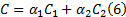
对 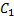

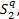
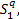
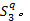
Step8 判断 

Step9 根据 
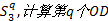


式中: 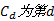
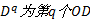
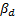
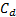

如果 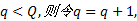
Step10 求当前时段 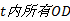
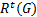
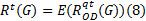
令 
为了保持可比性, 本文选用与文献[3]相同的实验环境与试验数据。
(1)分时可靠度对比
以采用文献[3]的算法进行各时段路网交通运行分时可靠度估计结果为基础, 计算本文算法估计结果的相对误差
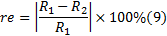
式中: 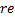


两种算法得到的试验路网分时可靠度及其相对误差如表1所示。
| 表1 两种算法的分时可靠度对比表 Table 1 Comparative table of analytic effect from two algorithms |
从表1可看出, 与文献[3]的算法相比, 本文算法对路网分时可靠度估计的平均相对误差为2.1%, 最大为7.69%, 最小为0。可以认为, 本文所设计算法在进行路网交通运行可靠性在线分析时可获得与文献[3]基本一致的效果。
(2)运行时间对比
以采用文献[3]算法进行各时段路网交通运行可靠度估计的计算时间为基础, 计算本文算法计算时间的节省百分比

式中: 
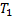
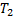
两种算法在路网分时可靠度估计时的计算时间及本文算法计算时间的节省百分比如表2所示。
| 表2 两种算法的运行时间对比表 Table 2 Comparative table of analytic efficiency from two algorithms |
由表2可看出, 与文献[3]算法相比, 本文算法运行时间的节省百分比平均为92.72%, 最大为99.45%, 最小为81.07%。可以认为, 本文方法能够显著提高路网交通运行可靠性在线分析的效率。
路网交通运行可靠性在线分析是交通系统可靠性研究领域的新课题, 对于改善动态交通管理决策的信息基础具有重要意义。针对已有成果运行效率偏低的问题, 本文借鉴邻接矩阵思想, 设计了路网可靠度表达与存储的新方法, 并设计了基于因子定理的路网交通运行可靠性在线分析方法。实证分析结果表明, 本文方法可在基本保持交通运行可靠度估计精度的同时, 显著降低在线运算的时间消耗水平, 可为进一步改善道路交通管理动态决策的及时性提供关键技术支持。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|