引用本文
赵丹, 邵春福, 岳昊, 李娟, 孟梦. 多方式诱导下基于出行链的随机用户平衡模型. 45(1): 82-88
ZHAO Dan, SHAO Chun-fu, YUE Hao, LI Juan, MENG Meng. Stochastic user equilibrium model based on trip chain analysis under multi-modal guidance. Journal of Jilin University Engineering and Technology Edition, 45(1): 82-88  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
多方式诱导下基于出行链的随机用户平衡模型
赵丹1,2, 邵春福1,2, 岳昊1,2, 李娟1,2, 孟梦1,2
1.北京交通大学 交通运输学院, 北京 100044
2.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室, 北京 100044
邵春福(1957-),男,教授,博士生导师.研究方向:交通规划, 交通安全, 智能交通.E-mail:cfshao@bjtu.edu.cn

作者简介:赵丹(1983-),女,博士研究生.研究方向:城市交通规划与管理.E-mail:08114188@bjtu.edu.cn

基金:国家自然科学基金项目(51178032, 11172035); “973”国家重点基础研究发展计划项目(2012CB725403); 中央高校基本科研业务费专项基金项目(2013JBM051); 国家“十二五”科技支撑计划项目(2013BAG18B01); 中国人民公安大学基本科研业务费项目(2014JKF1130)
摘要

为了评价多方式诱导信息对综合交通网络中交通流分配的影响,通过构建基于出行链的概率型随机用户平衡模型,并设计内嵌Monte-Carlo模拟的MSA求解算法,研究多方式诱导下组合出行方式选择、出行链费用和出行链结构的变化。求解过程中,引入超级网络理论,并基于超级网络进行流量分配。研究结果表明:多方式诱导信息使公共交通模式分担率增加5.63%,得到网络总收益为196.254,说明多方式诱导信息对引导出行者减少使用小汽车有显著效果,也有助于降低出行链费用,简化出行链结构。

关键词: 交通运输系统工程; 出行链; 随机用户平衡; 交通诱导信息; 组合出行方式
中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2015)01-0082-07
Stochastic user equilibrium model based on trip chain analysis under multi-modal guidance
ZHAO Dan1,2, SHAO Chun-fu1,2, YUE Hao1,2, LI Juan1,2, MENG Meng1,2
1.School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
2.Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Ministry of Education, Beijing 100044, China
Abstract

In order to evaluate the impact of multi-modal guidance information on the traffic assignment in the integrated transportation network, a trip-chain-based probit stochastic user equilibrium model was proposed to study the variations of travelers' choice of combined trip mode, trip-chain cost and trip-chain structure under the multi-modal guidance. A MSA algorithm with Monte-Carlo method embedded was presented to solve the model. In the model, travelers were divided into two groups by accepting multi-modal guidance information or not, and both groups make choices according to their own expected cost of trip chains. In the course of solution, hyper-network theory was introduced, and traffic flow assignment was carried out on the hyper-network. The results show that multi-modal guidance information helps to increase the mode split rate of public transport by 5.63%, and the network benefit reach 196.254. It can be confirmed that multi-modal guidance information contributes to encourage travelers to decrease the use of car, and reduce trip-chain cost and simplify trip-chain structure.

Keyword: engineering of communication and transportation system; trip chain; stochastic user equilibrium; traffic guidance information; combined travel mode
引言

国内外很多学者利用交通流分配模型研究交通信息的市场占有率、信息质量对出行行为及交通系统性能的影响, 研究表明:路网的不确定性导致了出行的延误成本[1, 2], 而信息服务对交通系统产生了正向影响[3, 4], 即随着信息的准确度和信息使用比例的在一定范围内的提高, 出行的不确定性降低, 交通系统的费用逐渐降低[5, 6]。但是, 上述研究中的交通信息多指道路交通流信息, 较少涉及公共交通信息领域; 并且是仅从单次出行的角度分析交通流分配情况及信息产生的影响[7, 8]。而实际出行中, 前次的出行和与之相连的下一次出行具有时间和空间上的承接关系, 前次出行的时间和目的地决定了下一次出行的出发时刻和路径选择, 仅研究交通信息对单次出行的影响是不全面的。因此, 有学者提出了基于出行链的交通分配模型, 如张伟华等[9]提出了基于出行链的弹性需求随机网络配流模型, Higuchi等[10]则建立了考虑共线性的多方式出行链交通分配模型。但是, 这些文献都没有考虑交通信息的影响, 将出行链交通分配模型与交通信息相结合的研究十分稀少。

本文在一种假设的“ 多方式诱导” 背景下, 从出行链的角度出发, 将出行者分为接受和不接受多方式诱导信息两类, 两类出行者根据各自对出行链的感知费用实现其选择行为, 通过建立随机用户平衡模型研究多方式诱导信息对综合交通网络中交通流分配的影响, 并分析出行者交通模式和出行链发生的变化。

1 多方式诱导下出行链费用分析

多方式诱导中“ 方式” 不仅指信息服务的媒介, 也暗含与多种交通方式相关的含义。总体上, 希望多方式诱导信息可以使出行链的全过程能够接受相关信息的辅助, 提高出行者选择方式、路径的正确率, 实现其出行费用的最小化。

1.1 模型假设

建立有向图G=(N, A)表示交通网络, 其中, N为节点集合, A为路段集合。定义a表示路段, a∈ A; ni 为驻点; 出行链记为c, c∈ C, C为可选出行链集合; ls 为连接出行链c中所有驻点的第s条可行路径, ls∈ Ω 。网络中存在三种交通工具, 记为R={auto, bus, metro}, 即小汽车、公交车和地铁, 三者组成五种交通方式, 记交通方式集合为{m|m=1, 2, 3, 4, 5}, 分别表示小汽车、公交车、地铁、公交车换乘地铁和小汽车换乘地铁。五种交通方式构成了三种交通模式:私人交通、公共交通和私人交通换乘公共交通(Park and Ride, 简称P+R换乘), m=1代表私人交通模型, m=2、3、4构成公共交通模式, m=5代表P+R换乘模式。

本文假设“ 多方式诱导” 提供三类信息:道路路段行程时间, 停车设施泊位情况, 公共交通工具等待时间, 其传播媒介包括交通广播、网络、车载导航、路侧信息提示屏、公交系统内部的视频装置等, 因此认为信息使用者占总体的比例(即信息的市场占有率)较高。分析出行链费用时, 主要基于以下假设:

(1)出行者可选交通方式齐全, 不考虑因受交通方式限制而导致只能选择某种交通工具的情况。

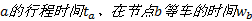
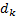
(2)出行者分为接受和不接受多方式诱导信息两类, 他们对路段 和在节点 的停车泊位寻找时间 的感知均存在误差, 这些误差均服从正态分布, 且接受者的感知误差更小。并且, 由于轨道交通线路独立, 认为其路段行程时间是固定的, 其路段行程时间的感知误差可以忽略。

1.2 出行链费用分析

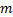
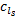
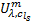
出行链可定义为由一系列驻点(指停留某处进行活动的地点)和路段构成的出行集合[11]。一般, 采用交通方式为 的出行链 的总费用 由确定项 和表示感知误差的随机项 构成, 即

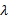
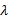
式中: =0表示不接受多方式诱导的出行者, =1为接受多方式诱导的出行者。

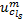
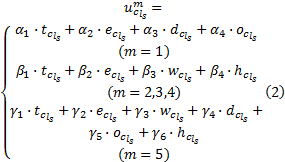
出行链总费用中的确定项 由构成其路径的路段、节点费用组成, 如式(2)所示:

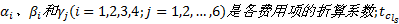
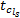
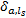
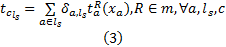
式中: 为路径行程时间; 为出行链中的停车泊位寻找总时间; 为等待公交车或地铁的总时间; 为使用交通工具产生的总经济成本; 为停车总费用; 为步行换乘消耗的总时间。

由出行链途经路段的行程时间构成, 令 为指示变量, 当路径 =1, 否则为0, 则

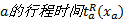
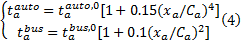
其中, 小汽车和公交车在路段 采用下面两个BPR(Bureau of public roads)函数计算:

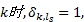
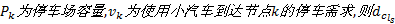
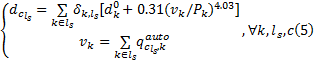
令 为指示变量, 当出行链经过节点 否则为0, 记 为自由流时寻找车位的时间, 的计算方法如式(5)所示:

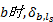
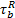
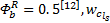
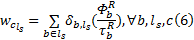
令 为指示变量, 当出行链路径经过节点 =1, 否则为0, 记 为节点 为与乘客到达分布特性及车辆间距相关的参数, 一般取 为:

根据式(2)中出行链总费用确定项的组成情况, 认为随机项 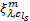中包含:

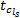
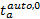
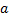
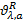
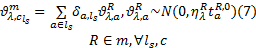
(1)对出行链行程时间 的感知误差 。由于地铁线路独立, 运行时间固定, 误差可以忽略; 令 和 分别为自由流时路段 上小汽车和公交车的行程时间, 设 则记 为出行链途经路段的行程时间感知误差 之和, 即

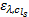
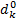
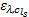
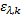
(2)使用小汽车出行时, 对停车泊位寻找时间 的感知误差 。令 为自由流泊位寻找时间, 设 , 则记 为出行链中包含的停车节点车位搜索时间感知误差 之和, 即

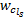
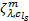
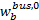
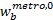
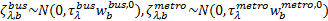
(3)使用公交车或地铁出行时, 对等车时间 的感知误差 。令 和 分别为自由流且非拥挤状态下的等待公交车和地铁的时间, 设 , 则记 为所有途经节点上等车时间的理解误差 之和, 即

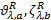
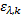
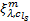
由于 和 独立并服从正态分布, 其线性和也服从正态分布。 表示为式(10):

式中:当出行链路径 并在该节点处停车时, 并在该节点处等车时, 否则为0。

2 随机用户均衡模型
2.1 模型建立

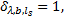
多方式诱导信息条件下, 出行者总是选择总费用最小的出行链, 依据随机用户平衡(Stochastic user equilibrium, SUE)的原理, 设 为不同类别出行者选择出行链 的概率, 则有:

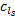
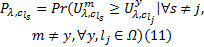
设具有出行链 则有式(12)(13)(14)成立:

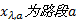
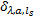
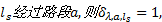
式(12)(13)(14)中: 的不同类型的出行者数量; 上的不同类型的出行者流量; 为指示变量, 若出行链路径 否则为0。

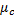
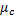
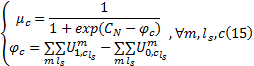
多方式诱导信息的市场占有率 对流量分配产生重要影响。设OD间出行需求 固定, 将Yang[13]的信息市场占有率 的计算公式引入模型, 如式(15)所示:

式中: 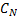为购买多方式诱导信息服务的价格; 为接受多方式诱导信息为出行者带来的收益。

根据市场占有率计算两类出行者的出行链流量, 如式(16)所示:

根据Sheffi和Powell[14]提出的与随机用户平衡等价极小值问题, 建立Probit型路径选择的出行链随机用户平衡数学规划模型, 如式(17)所示:

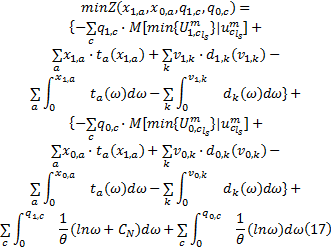
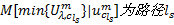
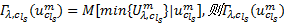
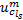
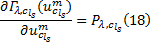
式中: 的最小出行费用的条件期望值, 令 需满足两个性质:一是该函数相对于 是凹的, 二是满足等式(18):

经证明, 式(17)与出行链随机用户平衡条件等价, 具体推导过程可参考文献[14]。

2.2 求解算法

连续平均法(Method of successive averages, MSA)是求解SUE问题的最有效算法之一。当MSA用于概率型的(Probit型)SUE问题时, 需进行双层迭代:一是内部“ 抽样/配流” 迭代; 二是外部平衡迭代。其中, 内部迭代通常采用Monte-Carlo模拟算法。本文设计的求解式(17)的算法步骤为:

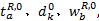
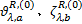
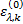
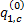
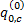
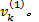
(1)初始化。设定市场占有率初值 确定 采用Monte-Carlo方法对两类出行者在自由流状态下的各项感知误差 和 进行抽样, 将 和 加载到网络上, 产生路段流量{ 停车流量 设置迭代次数L=1。

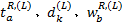
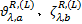
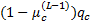
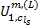
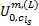
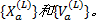
(2)更新出行链费用函数, 执行流量随机分配。确定各路段和节点的费用项, 如 等, 计算 采用Monte-Carlo方法随机抽取各项感知误差 和 得到总费用值 并将 和 分配到 和 最小的出行链上, 产生路段流量和停车流量的辅助值

(3)更新流量。 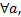令{ 计算

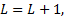
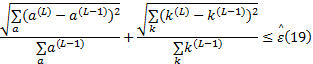
(4)收敛性检查。若满足收敛指标式(19), 则停止计算; 否则, 令 转步骤(2)。

式中:不等式左侧称为误差函数, 和 表示最后几次迭代的平均值。

3 算例分析

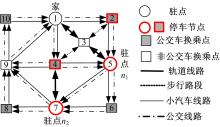
建立如图1所示的简化抽象综合交通网络, 表示从家出发依次经过驻点 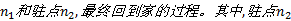为强制活动节点, 因此网络中至少存在两个OD对:(1, 7)和(7, 1)。图1中共有4个停车节点:2和4是小汽车换乘地铁的节点, 5和7为驻点停车场; 网络中各路段的参数见表1。

表1 路段参数 Table 1 Parameters of links

由于图1省略了进出交通网络的路段, 所以定义驻点属性时考虑了公交车、地铁的等车时间和小汽车泊位寻找时间的相关参数, 如表2和表3所示。

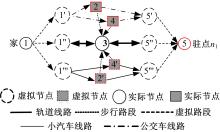
图1 基于出行链的综合交通网络Fig.1 Integrated transportation network based on trip chain

为了求解多方式交通流在网络中的分配情况, 通过增设虚拟节点和虚拟路段, 将小汽车和公交车分离, 建立超级网络。算例中流量加载和分配均基于超级网络进行。以在图1中“ 家→ 驻点n1” 所包含的路径和交通方式为例, 构造图2所示超级网络, 其他同理。图2中, 虚拟路段费用为0, 虚拟节点的参数与其对应的实际节点参数取值一致, 根据其所在线路的交通方式参照表2和表3进行定义。

表2 乘车节点处等车时间参数 Table 2 Parameters of waiting-time at boarding nodes
表3 停车节点处停车泊位寻找时间参数 Table 3 Parameters of searching-time at parking nodes

图2 “ 家→ 驻点n1” 的超级网络Fig.2 Hyper-network from home to stop n1

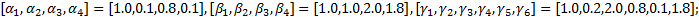
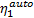
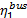
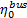
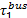
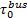
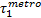
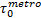
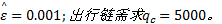
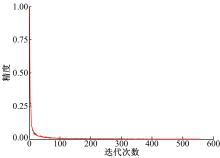
算例中, 设地铁票价为均一价2元, 公交车单位距离票价为阶段计价每10 km0.4元, 停车费见表3。其他参数取值分别为: 接受和不接受信息诱导的出行者感知误差的相关参数取值为: =0.4, =0.8, =0.6, =1, ρ 1=0.3, ρ 0=0.8, =0.5, =1.2, =0.2, =0.4, CN=1, =25%,

图3给出了算法的收敛性能。算法采用单步长迭代, 经过500多次迭代达到收敛标准。收敛时, 多方式诱导信息的市场占有率为31.17%。

图3 算法收敛图Fig.3 Convergence of algorithm

表4给出了均衡状态下, 接受和不接受多方式诱导信息的出行链流量分配结果, 以及5种交通方式的分担比例。可以看出, 无论是否接受多方式诱导信息, 使用小汽车完成出行链的交通方式划分率均为最高, 占总体的34.02%。比较两类出行者的选择情况, 发现接受多方式诱导信息的出行者更倾向于选择公共交通, 使用地铁和公交换乘地铁完成出行链的比例分别增加了6.35%和6.81%, 而小汽车、公交车和小汽车换乘地铁出行链的比例有所降低, 降低幅度分别为3.56%、7.53%和2.07%; 并且, 包含小汽车交通方式的私人交通模式和P+R换乘模式的分担率共下降5.63%, 而公共交通模式分担率则相应增加了5.63%, 说明多方式诱导信息可以促使出行者减少对小汽车的使用, 对引导私人交通转向公共交通有积极作用。

表4 多方式诱导信息对出行链交通方式划分率的影响 Table 4 Influence of multi-modal guidance information on trip-chain mode split rate%

表5列出了均衡状态下, 两类出行者的出行链平均费用差异。表5中的数值为每种交通方式对应的所有出行链路径费用的平均值。由表5可以看出, 接受多方式诱导信息后, 5种交通方式的出行链平均费用全部降低; 其中, 公交车出行链取得的收益最大, 达到0.067, 地铁出行链收益最小。原因在于:公交车的行程时间、等待时间等因素的不确定性最大, 不接受多方式诱导信息的出行者对上述因素的感知误差均大于其他交通方式。用每种交通方式的出行链费用平均收益乘以每种交通方式的流量分配结果(见表4), 得到网络总收益为196.254。

表5 多方式诱导信息对出行链平均费用的影响 Table 5 Influence of multi-modal guidance information on average cost of trip chain

表6列出了均衡状态下, 两类出行者的出行链结构特性差异。可以看出, 多方式诱导下, 包含驻点n1的出行链比例下降13.25%, 说明多方式诱导信息服务有助于简化出行链结构, 从而通过减少出行链中的出行次数, 取得减少出行总量的效果。

表6 多方式诱导信息对出行链结构的影响 Table 6 Influence of multi-modal guidance information on trip-chain structure
4 结束语

在多方式诱导的背景下, 从出行链的角度分析费用构成, 考虑出行者对不同类型和不同交通方式相关信息的感知误差, 建立基于Probit加载的随机用户平衡模型, 并运用内嵌蒙特卡洛(Monte-Carlo)模拟的MSA算法求解, 分析了多方式诱导信息对出行模式、出行链费用和出行链结构的影响。算例结果表明:多方式诱导信息服务有助于引导出行者减少对小汽车的使用, 并从私人交通转向公共交通模式; 出行者接受多方式诱导信息后, 各种交通方式的出行链平均费用全部降低, 网络总费用也随之下降; 并且, 接受多方式诱导信息的出行者更倾向于简化其出行链结构, 说明信息服务可以取得减少出行总量的效果。本文的一些参数是根据其他相关研究进行标定的, 对于实际的交通网络, 要根据实际数据标定参数。并且, 本文没有考虑小汽车与公交线路之间的影响, 今后的研究会将这一问题考虑在内。

The authors have declared that no competing interests exist.

参考文献
[1] Adler J L, Blue V J. Toward the design of intelligent traveler information systems[J]. Transportation Research C, 1998, 6(3): 157-172. [本文引用:1] [JCR: 2.006]
[2] Lo K H, Szato W Y. A methodology for sustainable traveler information services[J]. Transportation Research Part B, 2002, 36(2): 113-130. [本文引用:1] [JCR: 2.944]
[3] 姜桂艳, 郑祖舵, 白竹, 等. 拥挤条件下可变信息板交通诱导信息对驾驶行为的影响[J]. 吉林大学学报: 工学版, 2006, 36(2): 183-187.
Jiang Gui-yan, Zheng Zu-duo, Bai Zhu, et al. Simulation-based assessment of variable message signs route guidance information under congestion condition[J]. Journal of Jilin University (Engineering and Technology Edition), 2006, 36(2): 183-187. [本文引用:1] [CJCR: 0.701]
[4] Huang H J, Li Z C. A multiclass, multicriteria logit-based traffic equilibrium assignment model under ATIS[J]. European Journal of Operational Research, 2007, 176(3): 1464-1477. [本文引用:1] [JCR: 2.038]
[5] 吴文祥, 黄海军, 范景军. 交通信息对交通行为的影响和信息发布策略研究的一个新模型[J]. 系统工程理论与实践, 2008, 3(3): 144-150.
Wu Wen-xiang, Huang Hai-jun, Fan Jing-jun. A new model for studying impacts by traveler information systems on travel behavior and information release strategy[J]. System Engineering-Theory&Practice, 2008, 3(3): 144-150. [本文引用:1]
[6] Grotenhuis J W, Wiegmans B W, Rietveld P. The desired quality of integrated multimodal travel information in public transport: customer needs for time and effort savings[J]. Transport Policy, 2007, 14(1): 27-38. [本文引用:1]
[7] Li Z C, Lam W H K, Wong S C. Modeling park-and -ride services in a multimodal transport network with elastic demand [C]∥Transportation Research Record, 2007, 1994: 101-109. [本文引用:1] [JCR: 0.442]
[8] 孟梦, 邵春福, 曾靖静, 等. 停车换乘条件下组合出行模型及算法[J]. 吉林大学学报: 工学版, 2013, 43(6): 1465-1470.
Meng Meng, Shao Chun-fu, Zeng Jing-jing, et al. Model and algorithm of combined trip under park and ride[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(6): 1465-1470. [本文引用:1] [CJCR: 0.701]
[9] 张伟华, 隽志才, 倪安宁. 基于出行链的弹性需求随机网络配流模型[J]. 上海交通大学学报, 2009, 43(10): 1550-1554.
Zhang Wei-hua, Juan Zhi-cai, Ni An-ning. Trip-chain-based stochastic network equilibrium model with elastic demand [J]. Journal of Shanghai Jiaotong University, 2009, 43(10): 1550-1554. [本文引用:1] [CJCR: 0.411]
[10] Higuchi T, Shimamoto H, Uno N, et al. A trip-chain based combined mode and route choice network equilibrium model considering common lines problem in transit assignment model[J]. Procedia-Social and Behavioral Sciences, 2011, 20: 354-363. [本文引用:1]
[11] McGuckin N, Nakamoto Y. Trips, chains, and tours-using an operational definition[R]. Proceedings of National Household Travel Survey Conference Transportation, Washington D. C. , 2004. [本文引用:1]
[12] Lam W H K, Zhou J, Sheng Z. A capacity restraint transit assignment with elastic line frequency[J]. Transportation Research B, 2002, 36(10): 919-938. [本文引用:1] [JCR: 2.944]
[13] Yang H. Multiple equilibrium behavior and advanced traveler information systems with endogenous market penetration[J]. Transportation Research B, 1998, 32(3): 205-218. [本文引用:1] [JCR: 2.944]
[14] Sheffi Y, Powell W B. An algorithm for the equilibrium assignment problem with rand om link times[J]. Networks, 1982, 12(2): 191-207. [本文引用:1] [JCR: 0.645]