宋康(1987-),男,博士研究生.研究方向:汽车系统动力学.E-mail:bitsk@163.com
在1/4车辆模型的基础上建立7自由度人体-座椅-悬架模型。选取座垫加速度、悬架动挠度和车轮动载荷作为目标函数,根据参数灵敏度分析结果选择悬架和座垫参数作为设计变量。利用无量纲化消除多行驶工况对优化计算的影响,在此基础上建立了车辆行驶动力学性能多目标优化模型。选择带精英策略的非支配排序遗传算法(NSGA-II)对优化模型进行求解,得到了Pareto最优解集与Pareto前沿。优化结果显示:适当减小座椅座垫刚度并增大阻尼有助于改善乘坐舒适性并且几乎不影响其他性能;Pareto最优解集中的悬架刚度与阻尼呈线性正相关关系,这也决定了乘坐舒适性和悬架动挠度不可能同时达到最优设计;根据车轮动载荷的设计水平可以近似确定轮胎刚度。
A human-seat-suspension model with seven degrees-of-freedom was built on a 1/4 car model. The vertical acceleration, suspension work space and dynamic tire load were selected as the objective functions, and parameters of the suspension and seat cushion were selected as the design variables according to the results of parameter sensitivity analysis. Dimensionless method was introduced to make the optimization computation independent of the working conditions. Then a multi-objective optimization model was built to optimize the ride dynamic behavior of vehicle. Non-dominated Sorting Genetic Algorithm-II (NSGA-II) was employed for optimization computation and Pareto optimal set and Pareto frontier were obtained. Results show that seat cushion with small stiffness and large damping contributes to improve ride comfort without worsening other behaviors. In Pareto optimal set, the suspension stiffness is linearly directly proportional to suspension damping, which decides that optimal ride comfort and suspension work space can not be obtained simultaneously. Tire stiffness can be approximately determined based on dynamic tire load.
汽车的行驶动力学性能不仅直接关系到乘坐舒适性, 而且与操纵稳定性、安全性等性能密切相关。由于行驶动力学性能的各项常用评价指标之间相互矛盾, 因此, 在汽车设计中对各项性能进行权衡折中就成为必然的选择。随着优化技术的不断成熟及其在复杂机械系统设计中的成功应用, 汽车的优化设计问题吸引了越来越多的关注, 人们试图借助优化技术来实现汽车各项性能的全面提升。国外对汽车行驶动力学性能的优化已经开展了诸多研究。Alkhatib等[1]采用均方根值和绝对加速度灵敏度最小化的组合作为悬架优化的准则, 优化后的悬架对宽频激励具有良好的稳健性。Kuznetsov等[2]将人体的生物力学模型与1/4车辆模型相结合, 建立了人体-车辆-道路模型, 并借助该模型研究在指定的乘坐舒适性水平下悬架系统最优参数的确定。这些文献主要关注乘坐舒适性的优化, 并未全面考虑车辆的行驶性能。Gü ndo 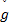
在经典的1/4车辆模型中, 通常采用车身加速度作为乘坐舒适性的评价指标。但是在实际的汽车中, 乘员是与带有弹性座垫的座椅直接接触, 某些车辆的座椅与车身之间设计有悬置装置, 并且人体自身也非刚体, 这些弹性、阻尼元素的引入使得直接采用车身加速度来评价乘坐舒适性并非十分准确。
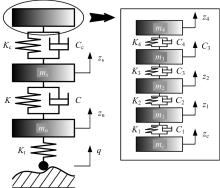
本文建立了7自由度人体-座椅-悬架模型, 力求更加准确地反映各弹性、阻尼元素对汽车乘坐舒适性的影响。人体模型包含4个部分, 从上到下依次为头部、上部躯体、下部躯体和大腿, 各部分相互之间以及人体与座垫之间均模拟为弹簧-阻尼连接; 座垫质量为mc, 刚度和阻尼分别为Kc和Cc。座椅通过导轨调节机构固定在车身上, 模型中简化为刚性连接, 其质量并入车身质量。座椅以下部分采用1/4车辆模型。完整的系统振动模型及相关参数表示在图1中。
首先建立该振动系统的运动方程, 以矩阵形式表示为:
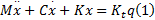
其中, 广义坐标向量:
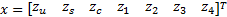
质量矩阵:

阻尼矩阵:
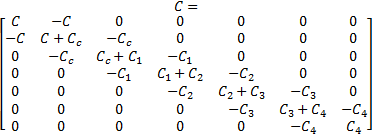
刚度矩阵:
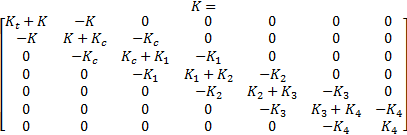
轮胎刚度矩阵:
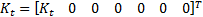
| 表1 系统模型参数值 Table 1 Values of system model parameters |
根据系统响应 x和路面激励q的傅里叶变换X(ω )和Q(ω ), 计算得到系统的频率响应函数矩阵H(ω )。H(ω )为7× 1阶列矩阵, 矩阵的第i个元素Hi (ω )(i=1, 2, …, 7)表示响应xi 对激励q的频响函数。
在构建优化问题时, 一般包括三个方面:合理制定目标函数, 正确选取设计变量以及建立二者之间的数学关系。
对于1/4车辆模型, 通常采用3个指标对行驶动力学性能进行评价, 即车身加速度, 悬架动挠度和车轮动载荷。由于本文建立的系统模型中引入了人体和座椅部分, 可以根据相关测试标准制定更加准确的指标以评价乘坐舒适性。根据GB/T4970-2009《汽车平顺性试验方法》, 测试中需要在座垫上方布置加速度传感器, 对照该模型可以认为此传感器布置于座垫mc处。如果忽略传感器与座垫之间的相互作用, 那么可以使用座垫mc的加速度来近似表示此加速度传感器的输出。因此, 本文采用座垫加速度、悬架动挠度和车轮动载荷的均方根值作为目标函数。下文中为表述方便, 在提及目标函数时不再特别指出均方根值。
目标函数的计算公式如下:
(1)座垫加速度(Vertical cushion acceler-ation, VCA)
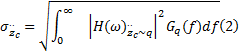
式中:频响函数 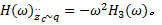
(2)悬架动挠度(Suspension work space, SWS)
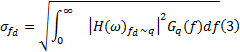
式中:频响函数 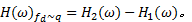
(3)车轮动载荷(Dynamic tire load, DTL)
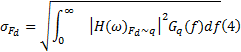
式中:频响函数 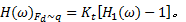
所制定的3项目标函数与悬架调校和座椅设计水平密切相关, 悬架和座椅的结构参数都可能选作设计变量。但是, 针对该优化问题作出如下假设:车身和底盘结构不发生变化, 各质量参数保持不变; 人体作为非优化对象, 所有相关参数均保持不变。因此, 模型中仅刚度和阻尼参数作为候选设计变量, 具体包括轮胎垂向刚度Kt、悬架刚度 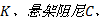
为了能够合理确定设计变量, 应用参数灵敏度分析技术研究各参数与目标函数之间的关系。由于各参数在数值上差别很大, 为了降低对优化计算产生的不利影响, 对各参数采用无量纲化处理, 即实际参与计算的设计变量为真实值与初始值的比值, 将所有参数的变化区间统一取为[0.5, 2.0]。
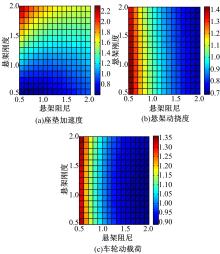
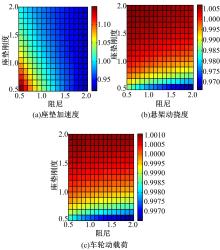
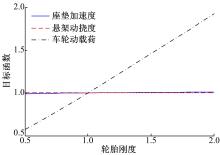
图2、图3和图4展示了各参数与目标函数之间的关系, 其中目标函数同样采用无量纲化的形式。
由图2(a)可以看出:当悬架刚度与阻尼同时取下限值时, 座垫加速度最小; 当悬架刚度取上限值而悬架阻尼取下限值时, 座垫加速度最大。另外, 当悬架刚度较小时, 阻尼的增加会增大座垫加速度, 而当悬架刚度较大时, 阻尼的增加会减小座垫加速度。图2(b)和(c)显示, 悬架阻尼对悬架动挠度与车轮动载荷有着十分明显的作用; 对于同一水平的阻尼值, 悬架刚度的变化对二者的影响不大。
由图3可以看出:座垫参数对座垫加速度的影响较为明显, 而对悬架动挠度和车轮动载荷的影响很小。
由图4可以看出:轮胎刚度与车轮动载荷近似呈线性关系, 而对座垫加速度与悬架动挠度几乎没有影响。
根据参数灵敏度分析的结果可以看出, 悬架参数的选择对目标函数的影响最大, 座垫参数主要对车辆的乘坐舒适性有影响, 而轮胎刚度则与车轮动载荷密切相关。根据分析结果决定, 悬架参数、座垫参数和轮胎刚度均选作设计变量参与优化计算。
在建立优化模型时需要考虑车辆不同行驶工况的影响。行驶工况变化的最直接作用在于改变系统的路面功率谱密度输入。已知时间频率 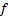
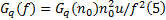
式中: 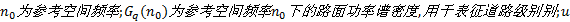
根据式(5)可以看出, 路面输入受到行驶车速 u和道路级别Gq (n0)的共同影响。既然汽车在行驶过程中不可避免地要出现行驶工况的变化, 那么在建模时就有必要考虑不同工况对优化计算所产生的影响。
假设汽车在A工况下的行驶车速为 u, 路面在参考空间频率n0 下的功率谱密度为Gq (n0), 此时设计变量与第i项目标函数之间的关系如下:
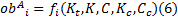
式中:计算得出的目标函数值 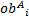
如果目标函数以无量纲形式进行表示, 那么无量纲化的新目标函数 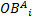
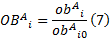
式中: 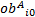
接下来考虑另一种工况B。假定汽车在B工况下的车速为 au, 路面在参考空间频率n0 下的功率谱密度为bGq (n0), 其中a和b都是无量纲的比例系数, 那么设计变量与第i项目标函数之间的关系将变为如下形式:
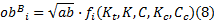
式中:计算得到的目标函数值 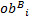
可以看出, 两种工况下的目标函数之间满足关系式:
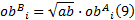
同样对B工况下的目标函数进行无量纲化, 处理之后的新目标函数 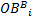
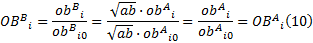
根据式(10)可以看出:虽然模型在B工况下计算得到的目标函数绝对量相对A工况变化了 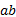
基于悬架的簧载质量偏频和阻尼比提出该优化问题的两个约束。统计结果显示[8], 悬架的偏频和阻尼比并不是随意确定的, 而是有一定的分布范围。前悬架偏频的分布范围为0.8~1.45 Hz, 后悬架偏频的分布范围为0.98~1.58 Hz, 阻尼比的分布范围为0.2~0.4。该车辆模型的偏频 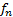
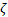
在完成上述问题的讨论后, 正式提出本文的优化模型。选择车速60 km/h, B级路面作为行驶工况, 5项设计变量的取值范围均为[0.5, 2.0], 优化计算中的设计变量值和目标函数值均采用无量纲化形式。多目标优化模型如下:
min 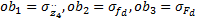
s.t. 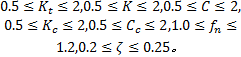
处理多目标优化问题的方法通常分为归一化方法(加权法)和非归一化方法。非归一化方法采用Pareto机制直接处理多个目标, 不需要进行加权处理。多目标遗传算法是最常用的非归一化方法之一, 可以一次性得到Pareto前沿。本文采用多目标遗传算法系列中带精英策略的非支配排序遗传算法(Non-dominated sorting genetic algorithm-II, NSGA-II)进行优化问题的求解, 该方法探索性能好, Pareto前进能力强。
由于多目标优化问题一般得不到绝对最优解, 因此计算的目的就是为了得到非劣解的集合, 即Pareto最优解集。图5为经过优化计算得到的Pareto最优解集, 以及Pareto最优解集在目标函数空间中的映射— — Pareto前沿。其中, Pareto最优解集分为两部分进行表示, 图5(a)表示悬架系统参数, 包括悬架刚度、悬架阻尼和轮胎刚度; 图5(b)表示座椅参数, 包括座椅刚度和座椅阻尼; 图5(a)和图5(c)中还同时给出了Pareto最优集和Pareto前沿在各坐标面上的投影。
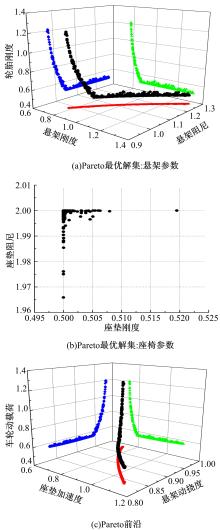 | 图5 多目标优化问题的Pareto最优解集及Pareto前沿Fig.5 Pareto optimal solver set and Pareto frontier of multi-objective optimization problem |
由图5可知:在设计变量空间中, Pareto最优解集中的悬架参数呈线型分布形式, 而座垫参数则呈聚集分布形式。在目标函数空间中, Pareto前沿也呈线型分布形式。
根据参数灵敏度分析结果可知, 座垫参数主要影响乘坐舒适性, 对悬架动挠度和车轮动载荷影响很小。因此, 当座垫具有低刚度、高阻尼属性时, 有助于提高乘坐舒适性并且几乎不损害另外两项性能。同时, 由于座垫参数的(稳定)聚集分布, Pareto前沿的分布形式主要受悬架参数的影响, 二者在各自的空间中均呈线型分布。
在悬架参数空间中的Pareto最优解集可以分为两部分:沿直线分布的部分对应轮胎刚度保持不变, 仅悬架刚度和阻尼发生变化; 沿曲线分布的部分对应三者同时发生变化。首先分析前一部分。由于轮胎刚度主要影响车轮动载荷, 对另外两项性能几乎没有影响, 因此, 当轮胎刚度取下限且保持不变时, 车轮动载荷性能达到最优, 这就对应了Pareto前沿中车轮动载荷性能保持不变的部分。另外, 根据Pareto最优解集在悬架刚度-悬架阻尼平面上的投影可以看出, 二者近似呈线性正相关关系, 同时增大或减小。当轮胎刚度保持不变, 悬架刚度和阻尼同时增大时, 根据参数灵敏度分析结果可知, 乘坐舒适性能将恶化, 而悬架动挠度性能将得到改善, Pareto前沿清楚地显示了该分析结果。接下来分析后一部分。在该部分中, 当轮胎刚度增大时, 悬架刚度和阻尼会同时减小。轮胎刚度的增大意味着车轮动载荷性能将会恶化, 悬架阻尼的减小意味着悬架动挠度性能将会恶化, 二者的变化趋势一致, 但是悬架刚度的减小却会改善乘坐舒适性能。另外, 由于悬架刚度和阻尼的变化关系相对固定, 这就决定了乘坐舒适性和悬架动挠度必然不可能同时达到最优, Pareto前沿在座椅加速度-悬架动挠度平面上的投影显示了该分析结果。
综上所述, 当由第一部分选择设计方案时, 车轮动载荷性能达到最优且保持不变, 在此前提下根据其他性能的设计要求确定悬架刚度和阻尼; 当由第二部分选择设计方案时, 车轮动载荷性能的变化范围很大, 但是在每个水平上都只与其他性能唯一对应, 这样确定的每组设计方案都对应各项性能完全不相同的组合。
(1)建模过程中引入人体和座椅部分与1/4车辆模型相结合, 根据汽车平顺性测试标准, 以座垫加速度来近似模拟布置于座垫上方的加速度传感器输出, 从而制定出更接近实际测试状态的乘坐舒适性评价指标。
(2)利用无量纲化消除多行驶工况对行驶动力学性能优化计算的影响, 优化建模时可以只选择一种典型工况作为代表即可。
(3)适当减小座椅座垫刚度并增大阻尼有助于改善乘坐舒适性并且几乎不影响其他性能; Pareto最优解集中的悬架刚度与阻尼呈线性正相关关系, 这也决定了乘坐舒适性和悬架动挠度不可能同时达到最优设计; 根据车轮动载荷的设计水平可以近似确定轮胎刚度。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|