作者简介:孙强(1987-),男,博士研究生.研究方向:车用油电混合动力技术.E-mail:sunqiangsdu@163.com
以环卫车运行工况为研究对象,通过对西安市环卫车运行工况的试验测量,利用两阶段聚类法构建西安市环卫车典型行驶工况。引入运动区间的概念用于描述运动学片段的瞬时特征,以运动学区间相关参数为特征参数对片段类内的片段进行第二阶段的聚类,实现对类内特征片段的提取和组合,完成典型行驶工况的构建。最后,通过与单次聚类法构建工况的对比,验证使用两阶段聚类法构建车辆瞬时行驶工况的合理性。对比结果表明:两阶段聚类法与传统单次聚类法相比,在速度分布、加速度分布以及速度-加速度联合分布上分别有59.4%、81.7%和22.4%的改进。
A two-stage clustering method is proposed to construct the driving cycle of garbage truck. In this method, first the concept of kinematics interval is put forward to describe segment's instantaneous characteristics, upon which an advanced hierarchical clustering is carried out. Second, proper segments are chosen from each category according to the results of the second stage clustering. Finally, the representative driving cycle is fitted out. The proposed method is applied to construct driving cycles of a typical garbage truck in Xi'an City. For comparison a driving cycle is also constructed using traditional clustering method, actual driving cycle is measured and error analysis is carried out. Results show that compared to the traditional clustering method, the two-stage clustering method can improve the probability distribution of speed by 59.4%, the probability distribution of acceleration by 81.7%, and the joint probability distribution of speed-acceleration by 22.4%.
汽车行驶工况是某一类车辆在特定时间、空间条件下的速度-时间历程, 主要用于确定车辆的油耗及排放测试, 是汽车工业一项共性核心技术[1, 2, 3, 4, 5, 6, 7]。在世界范围内, 被广泛使用的典型工况有:美国行驶工况(FTP75)、欧洲行驶工况(ECE15+EUDC)和日本行驶工况(JPAN10)[8, 9, 10, 11]。目前, 我国采用欧洲行驶工况作为测试循环[12], 但我国实际道路状况与欧洲存在着显著的差异, 研究符合我国交通特征的车辆行驶工况具有重要的意义。近年来, 国内学者对行驶工况进行了一系列研究并取得了一些成果:石琴等[3, 4]利用组合聚类法及FCM聚类法对合肥市实际道路工况进行研究并建立合肥市区的典型行驶工况; 杜爱民等[9]对上海市公交车行驶工况进行调查研究并构建了上海市公交车典型行驶工况; 庄继辉等[10]对天津市纯电动汽车道路行驶工况进行了研究, 构建了适用于天津市的纯电动汽车行驶工况; 李孟良等[11]结合天津市道路情况对行驶工况解析方法进行了研究; 黄万友[12]对济南市纯电动汽车道路行驶工况进行了研究并构建了济南市小型纯电动汽车行驶工况。
上述行驶工况的研究都遵循着如下流程:试验测量→ 原始数据获取→ 特征值分析→ 片段类别划分→ 代表片段抽取→ 典型工况合成。先前的研究都集中于特征值分析和片段类别划分两个步骤, 而在代表片段抽取阶段采用简单的处理方法, 如采用随机抽取[9, 13, 14, 15, 16]和基于片段类内全部特征值的抽取[3, 8, 10]。针对代表片段抽取阶段, 本文引入运动学区间的概念来描述运动学片段的瞬时特征, 采用运动学区间相关参数对每个片段类进行第二阶段的聚类, 并以聚类的结果作为依据进行代表片段抽取和典型工况合成。最后, 通过与传统方法构建工况的对比分析, 证明本文所提方法的有效性。
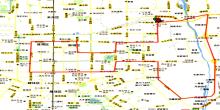
以28 t某型城市环卫车行驶工况为研究对象。线路选取结合西安市道路实际特点和环卫车工作特点, 综合考虑区域类型、道路类型、车流密度等因素, 最终选择图1所示的道路进行测试。
所选道路全程共42 km, 所经过的区域包括商业区、居民区、工业区等典型的环卫车工作区域, 所经过的道路包括主干道、次干道及外环路等典型道路。
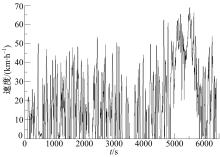
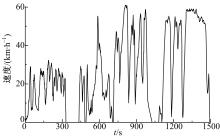
测量时间选取7∶ 00~10∶ 00, 14∶ 00~16∶ 00, 17∶ 00~19∶ 00三个时间段, 涵盖每天交通的高峰和低峰期。测量连续进行7天。工况参数测量和记录的频率为1 Hz。通过测量, 获取到涵盖792.3 km路程的12万组有效测试数据。图2为其中一次道路测试的实测工况。为对测试数据进行统一归类与分析, 需要对原始测量数据进行运动学片段划分、特征参数选取、特征参数计算及标准化等预处理。
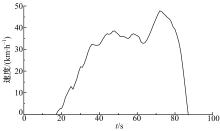
运动学片段定义为车辆从一次停车开始到下一次停车为止的运动[12]。图3为图2中的第22个运动学片段。运用Visual C++编程, 对原始测量文件进行划分, 最终获得1283个类似的运动学片段。
为准确地反映运动学片段的瞬时特征, 本文定义了运动学区间的概念, 并以运动学区间为基本单位将运动学片段进一步划分。运动学区间定义为:在同一个运动学片段内, 具有相同运动学参数的连续的时间片段。此处运动学参数包括速度 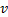
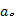
特征参数是运动学片段的评价准则[15, 16]。本文将特征参数分为如表1所示的整体特征参数和瞬时特征参数两大类:整体特征参数用于描述运动学片段整体特征量, 如片段时长、平均速度、加速时间等; 瞬时特征参数用于描述运动学片段瞬时特征量, 主要描述运动学区间相关参数, 如加速区间数、加速区间长度、加速区间长度标准差等。其中整体特征参数用于第一阶段聚类, 是划分片段类的依据; 瞬时特征参数用于第二阶段的聚类, 是代表片段抽取和组合的依据。
| 表1 描述运动学片段的特征参数 Table 1 Kinematic segment characteristic parameters |
特征参数确定后, 需要对1283个运动学片段分别求取其26个特征值, 该部分工作在Excel中利用VBA编程实现。最终获得一个1283× 26的特征参数矩阵 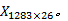
因不同参数的量纲不同, 其数值范围相差很大, 而这种由于变量各分量离散程度不同导致的差异不能反映数据本身的变化情况[15]。为消除这种影响, 对特征参数矩阵 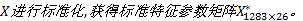
第一阶段聚类的目的是在整个样本空间的范围内以运动学片段的整体特征参数为依据对运动学片段进行分类。因其发生在道路片段类之间, 故将其称之为类间聚类分析。
本文利用统计分析软件SPSS对矩阵 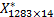
| 表2 各成分特征值、贡献率及累计贡献率 Table 2 Eigen values, contribution rates and cumulative contribution rates of each component |
研究表明[3, 16], 主成分累计贡献率达90%以上即可满足车辆实际行驶工况的开发需求。由表2易知, 取前5个主成分时累计贡献率即能达到91.89%。
按照聚类方法不同, 聚类分析又可分为:系统聚类法、动态聚类法、有序聚类法等[12, 14, 15]。这些方法中, 系统聚类法不要求对未分类数据有先验经验, 即无需确定初始分类数和初始聚类中心, 考虑到无法确定片段分类数和片段初始聚类中心, 本文选用系统聚类法对运动学片段进行分类。
利用SPSS, 采用系统聚类法, 以离差平方和作为样本相似性度量, 以2.1节中获得的5个主成分为分类参数, 对样本进行聚类分析。按照离差平方和的算法, 类间距为0或1时, 每个样本自成一类, 因此类间距的选择应大于1。为能详细描述不同分类间的差异, 本文选用离差平方和为2时的分类, 最终将1283个运动学片段划分为5类, 各分类特征值如表3所示。
| 表3 各分类整体特征参数值 Table 3 Overall characteristic parameters of each category |
对比表3中不同类别的特征参数值可以发现它们间存在显著的差异:类1, 片段数目少、片段持续长、平均速度和最高速度高, 该分类能反映所测路线中的外环道路工况; 类3, 片段数目多、片段持续时间短、平均速度和最高速度低, 该分类能反映环卫车在垃圾收集点工作或通过红绿灯时频繁短程移动的工况; 类2、4、5, 其特征参数值介于类1和类3之间, 片段数目多, 持续时间从69 s至177 s、平均速度从11 km/h到37 km/h, 属于典型的市区道路工况, 而这三类的之间差异则反映的是不同时间段或不同路段间道路状况的差异。
第二阶段聚类的目的是, 在同一个道路片段类内以运动学片段的瞬时特征参数为依据对运动学片段进行分类, 并以分类结果作为代表片段抽取的依据。因其发生在道路片段类之内, 故将其称之为类内聚类分析。具体过程以片段数最多的类5为例说明。
根据类内聚类分析定义, 类内聚类分析的特征参数应该是瞬时特征参数, 样本空间范围是类5内的样本。除特征参数及样本空间范围不同外, 该过程与2.1节所述一致, 前7个主成分特征值、贡献率及累计贡献率如表4所示。
由表4易知, 取前7个主成分时累计贡献率达到93.08%, 故选用前7个主成分来替代全部12个参数。
| 表4 各成分特征值、贡献率及累计贡献率 Table 4 Eigen values, contribution rates and cumulative contribution rates of each component |
同样地, 因为没有区分样本类别的先验经验, 此处也选用系统聚类法。聚类获得的可用分类数为 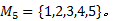
与类间聚类采用尽可能多的分类数不同, 类内聚类的最终分类数由可用分类数和可用区间数共同决定, 其中, 可用区间数由下式确定:
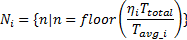
式中: Ni 为第i类可用区间数的集合; Ttotal 为合成路谱的总时长; η i 为第i类的分类时长与样本总时长之比; T avg_i为第i类的片段时长特征值, floor()表示对数值进行向下取整。
类1~类5对应的 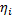
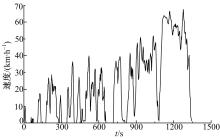
结合2.3节中对片段分类结果的分析和3.3节中运动学片段的抽取结果, 片段组合按以下顺序进行:频繁短行程工况(类3), 典型市区道路工况(类2、类4和类5), 城市外环道路工况(类1)。同一片段类内运动学片段组合顺序由表5中的抽取顺序(SPSS分类时确定)确定。组合成的代表工况如图4所示。
采用传统的单次聚类法, 以表1所示的26个特征参数为分类依据做主成分分析及聚类分析, 并随机抽取运动学片段组合成代表工况, 如图5所示。
4.2.1 基于速度、加速度分布的有效性分析
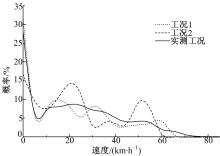
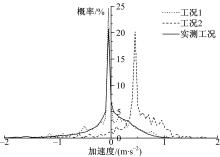
分别求得两阶段聚类法构建工况(以下简称工况1), 传统单次聚类法构建工况(以下简称工况2)以及实测工况的速度分布和加速度分布图, 如图6和图7所示。
对比图6和图7可知, 工况1在速度、加速度分布上比工况2更为接近实测工况。为定量描述速度分布的接近情况, 将求得的速度分布向量看做 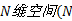
4.2.2 基于速度-加速度联合分布的有效性分析
车辆的运动状态由速度和加速度共同决定, 速度或加速度单独的分布无法全面描述车辆真实状态的差异, 为进一步描述3个工况中车辆所处状态的差异, 求得3个工况的速度-加速度联合概率密度分布如图8所示。
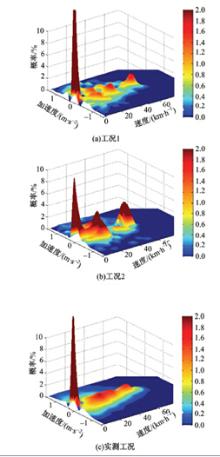 | 图8 三种工况速度-加速度联合概率密度分布图Fig.8 Speed-acceleration joint probability density distribution of three conditions |
对比3种工况联合概率密度分布图易知:实测工况概率密度分布最为均匀、连续; 工况1、工况2概率密度分布的趋势与实测工况基本一致, 但分布的均匀性及连续性上工况1更接近实测工况。为定量描述三者间差异, 分别求得工况1、工况2与实测工况的速度-加速度分布的欧式距离。求得的距离分别为5.9和7.6, 工况1与工况2相比, 在速度-加速度分布上有22.4%的改进。
引入运动区间的概念用于描述运动学片段的瞬时特性, 并以此为依据对运动学片段的抽取过程进行第二阶段的聚类分析。在西安市环卫线路的测量的基础上, 分别利用本文所提的两阶段聚类法和传统的单次聚类法提取代表工况, 并通过速度-加速度状态分布将两个合成工况与实测工况对比、分析, 检验本文所提方法的有效性。
速度-加速度状态分布的分析结果表明:本文所提的方法能显著提高构建路谱的速度-加速度分布情况, 与单次聚类相比, 在速度分布、加速度分布和速度-加速度联合分布上分别有59.4%、81.6%和22.4%的改进。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|