刘华胜(1987-),男,博士研究生.研究方向:交通运输系统规划.E-mail:liuhs12@mails.jlu.edu.cn
通过建立基于有效路径的双目标模型来解决接运线路设计问题。首先,运用复杂网络介数概念,在考虑城市拥堵的基础上定义有效路径作为接运线路设计的基础;以乘客出行时耗最小和运输效率最大为目标,同时考虑线路长度、非直线系数、线路运能等约束设计接运线路模型;借鉴“逐条布设,优化成网”思想,设计模型的具体求解步骤;最后,以长春市轻轨4号线作为接运对象进行实证分析。结果表明:在交通拥堵的情况下,该模型所设计的接运线路更能体现居民出行路径的选择策略。
A two-target model based on effective path is established to solve the Feeder Bus Network Design Problem (FBNDP). First, the effective path concept is defined on the basis of complex network betweenness considering urban traffic congestion, which is the basis of the design of feeder bus network. Taking into account the constraints such as the line length, non-linear coefficient, transport capacity etc., the two-target model is established, in which the minimization of passenger travel time and maximum of the transport efficiency are taken as the targets. Then referring to idea of "Combined Each Route, then Form the Network", the solution approach to the model is proposed. Finally, the model is applied to the Light Rail Transit 4 of Changchun. The results show that the feeder bus network designed by the model in the presence of traffic congestion can reflect the residents' travel selection strategy better.
接运公交是指以轨道交通接运乘客为主要功能的公共交通方式, 是常规地面公交系统的一部分, 与轨道交通线网共同组成轨道交通接运公交系统[1]。接运公交设计问题(Feeder bus network design problem, FBNDP)是确定包括接驳车站、线路经由、开行频率三部分内容的城市常规公交接驳线路方案[2, 3]。本文主要对接运网络设计问题进行研究。网络设计问题是指通过给定的交通需求、区域的拓扑特征、设置的目标和约束条件来确定一组适中的特定区域公交路线[4]。对于接运线路设计, 已有研究主要以运营者、乘客和社会成本最小为目标, 建立线路设计模型[5, 6, 7], 模型求解多以启发式算法为主[8, 9]。多数研究未考虑路网拥堵对线路布设的影响, 涉及企业运营目标多考虑成本因素, 忽视了公交公益性。本文在考虑城市道路拥堵的情况下, 提出基于有效路径的接运公交线路设计模型, 模型目标同时考虑了乘客及运营者因素, 给出了模型的具体求解步骤, 该模型可作为FBNDP方法的有效补充, 同时为城市公共交通一体化网络布局提供理论支撑。
对出行者而言, 其出行行为决策所考虑的重要因素是能否以最短时间到达目的地。当路网上个体数目较少, 网络交通流保持在自由流状态时, 最短路出行策略是有效的; 而对于大城市而言, 由于交通拥堵或流量限制, 最短路往往不是出行时间最短的路径, 通过交通量较大的路段或节点往往更容易产生交通拥堵进而引发网络级联失效, 个体就可能花费更多的时间来通过这个节点。而适当避开该类路段或节点, 选择有效路径则可能花费更少的出行时间, 并能保证出行时间的稳定性。常规公交运营具有“ 五定” 特点, 乘客一旦选择该线路则无法通过绕行来避免拥堵导致的出行成本增加, 尤其对于必须经过换乘才能到达目的地的乘客, 他们所考虑的更重要的因素是出行时间的稳定性。因此, 公交线路的布设应考虑适当避开拥堵现象比较严重进而容易发生级联失效的路段或节点。
介数是复杂网络理论中的重要概念, 分为边介数和点介数。节点的介数为网络中所有最短路径中经过该节点的数量的比例, 边的介数含义类似。介数反映了相应的节点或者边在整个网络中的作用和影响力。点i的介数Bi可由下式进行计算[10]:
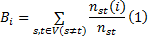
式中: nst 为连接点s和t的最短路径的数量; nst (i)为连接点s和t且经过点i的最短路径的数量; V为网络节点的集合。同理, 与节点 i 连接的边e(i)的介数Π (e(i))可由下式进行计算:
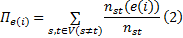
基于介数概念定义有效路径, 对于节点 s和t之间的路径P(s→ t):=s≡ x0, x1, …x (n-1), xn≡ t, L(P(s→ t):φ )为对于给定参数 φ 的s和t之间的阻抗, 记:

节点 s和t之间有效最短路径是使L(P(s→ t):φ )达到最小值的路径, 其中 φ 为参数, n为路径途经的不包括起点 s的个数, f(e(i)))为路段 e(i)的阻抗。
基于有效路径的定义, 当 φ =0时, 居民出行策略为传统的基于最短路的出行; 当 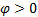
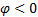
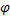
考虑分析问题需由简到繁, 在此对问题进行简化, 提出以下假设:①轨道交通线网、运能及发车间隔确定并已知; ②接驳线路布设所基于的公交网络状态为对现状公交线路优化调整后的公交网络, 即排除当前网络不合理造成的接运线路设计不合理因素; ③通过预测或调查, 全方式及公交客流需求OD已知, 轨道交通直接吸引的直达客流OD已知; ④公交站点为需求产生点, 即将公交站点作为客流始发和终到的目的节点, 不考虑乘客由起点和终点至公交或轨道交通停靠站消耗的时间; ⑤每一条公交线只连接一个轨道站点; ⑥一定时期内客流需求稳定, 不考虑其他因素导致的客流需求弹性。
公共交通具有公益属性, 所提供服务的目的是在能够维持正常运营的基础上满足居民的公交出行需求, 企业应该通过优化布设公交线路达到运输效率最大化而不是利润最大化, 以此来间接降低运营成本; 无论是否存在换乘, 所有出行者均希望在可接受的支付成本下, 以最快的速度到达目的地, 对于换乘者, 则希望尽量减少换乘次数和缩短由于换乘增加的出行时间, 同时保证出行时间的稳定性。因此设定接运线路设计目标如下:
(1)乘客出行时耗最小
定义1 乘客出行时耗最小化程度是乘客理想总出行时间与线路布设后乘客总出行时间的比值, 其中乘客理想总出行时间为所有OD对 (s, t)的乘客量Q (s, t)与(s, t)最短出行时耗d(s, t)乘积的总和; 线路布设后乘客总出行时间为乘客所有出行时耗, 包括站点候车时间 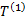
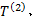
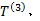
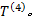
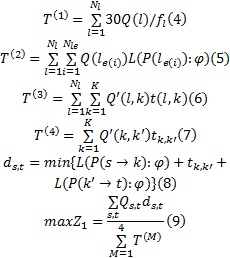
式中: Q(l)为线路l运送的客流量; Q(l e(i) )为线路l中e(i)路段的断面流量; fl为线路l的发车频率; L(P(l e(i):φ )为对于给定的参数 φ , 线路 l中e(i)路段的路径阻抗; Q'(l, k)为线路l的接运站与轨道交通站点k间的换乘量; t(l, k)为公交线路l的接运站与轨道交通站点k间的步行时间; 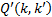
(2)运输效率最大
定义2 运输效率为换乘旅客周转量与所提供的运能之比, 计算公式为:
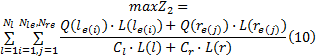
式中: L(l)、L(r)和L(le(i))、L(re(j))分别为公交l和轨道r线路长度和各自路段 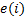
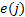
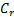
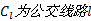
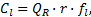
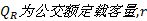
(1)线路长度
线路长度与城市规模、居民出行距离、公交运送速度等因素有关, 约束条件记为:
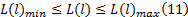
式中: 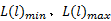
(2)线路非直线系数
线路非直线系数是指公交线路长度与该线路起点终点之间直线距离 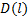
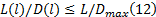
线路非直线系数 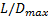
(3)站点停靠能力
通常情况下, 单位时间线路在站点停靠的车辆数不应超过站点 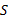
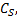
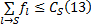
式中: 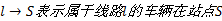
(4)线路断面不均衡系数
线路断面不均衡系数 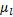
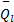
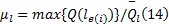
式中: 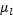
(5)公交线路客运能力
受实际投入的车辆规模限制, 常规公交线路最大断面客流量不能超过线路提供的运能, 记为:
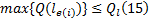
(6)轨道交通客运能力
轨道交通接运客流量不能超过该断面剩余客运能力, 记为:
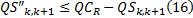
式中: 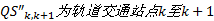
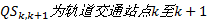
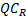
本文借鉴“ 逐条布设, 优化成网” 思想[1], 设计如下步骤进行模型求解:
Step1 道路网络初始化及求解有效路径参数 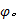
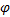
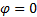
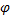
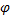
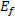

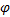
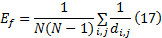
式中: di, j为研究时段内节点i和j间的最短出行时耗。
首先初始化所研究的网络并划分交通小区, 设定道路通行能力、通行速度等参数, 计算自由流通行时间T0, 通过调查获得区域内高峰小时全方式客流OD, 采用随机用户平衡分配法将OD分配到路网上, 得到各路段通行时间T1。根据文献[12], 取 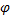

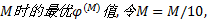
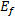

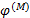
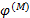
Step2 获取用于布设接运线路的OD矩阵。首先通过调查或预测获取研究范围内高峰时段的公交客流OD矩阵 

考虑到接驳线路布设前, 已存在部分公交线路与轨道交通站 k'形成自然接驳产生换乘客流, 因此应剔除该部分客流, 定义参数δ 'i, j如下:
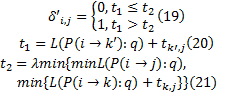
式中: 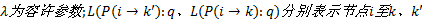
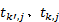
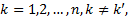
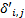
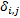
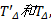
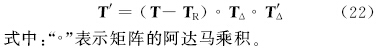
Step3 确定备选接运站及首末站。接运公交线路规划的关键是接运站点的选取以及接运路线的优化, 因此应首先确定备选站点集合。接运站点应选择潜在换乘客流量较大且有剩余载客容量的轨道站点。轨道交通站点 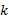
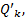
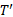
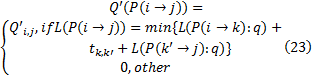
式中: Q'(P(i→ j))表示通过路径P(i→ j)的客流量, 则可求得加载到轨道交通站点k至k+1的断面潜在流量:
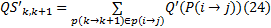
通过轨道直达运送客流矩阵以及原有换乘客流矩阵, 可得到轨道交通站点 k至k+1的背景断面流量QSk, k+1, 根据轨道交通运行情况得到最大断面运能 
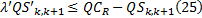
式中: 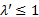
可以得到轨道交通备选接运站点集合 K', 对该集合中的站点进行分类, 对于有换乘场地的站点标记为k's。对常规公交站点设定如下集合:
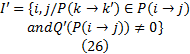
选择该集合中与轨道交通线路垂直距离最长和次长、且有预留用地的常规公交站点作为备选首末站, 此外接运区域内原有或预留的公交首末站或换乘枢纽也作为备选首末站, 共同组成集合 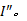
Step4 建立备选线路集。接运备选线路搜索中, 最短有效路径未必能满足单线路约束条件, 其次短路或者 
(1)对基于最优参数 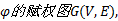
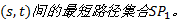
(2)在最短路径集合 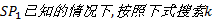
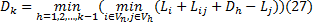
式中: 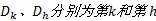
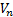
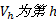
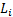
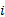
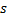
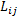
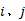
当次短路最短路长度超过线路长度约束时停止搜索, 由此构成 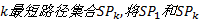
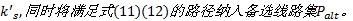
(3)将 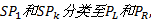
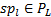
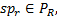
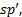

Step5 最优线路选择及OD矩阵更新。对于多目标最短路问题, 一般不存在单一的最优解, 而是一个Pareto解集。基于此, 本文设计如下算法求得满意路径:
(1)考虑式(13)~(16)的约束条件, 基于获取的OD矩阵, 计算所有备选线路集合Palt中的线路对应的目标函数值, 记 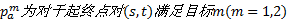
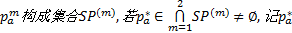
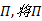
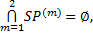
(2)记 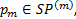
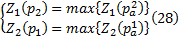
令目标 Z1值在区间[Z1 (p2), Z1 (p1)]的路径集合为Π ', 令目标Z2 值在区间[Z2 (p1), Z2 (p2)]的路径集合为Π ″, 则存在Π =Π '⋂Π ″≠ ∅, 将Π 中无路段重合的路径布设在网络中, 并在备选线路中剔除该路径, 转至第(3)步。
(3)对OD矩阵及剩余客运能力进行更新。每布设一条线路, 在原有OD中剔除该线路运送的客流量, 同时更新轨道交通剩余客运能力。
(4)转至第(1)步, 重新确定最优线路, 当所有首末站间都布设一条有效接运线路时, 算法停止。
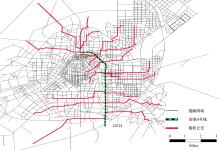
本文结合《长春经济技术开发区公共交通规划(2011-2020)》, 以长春轻轨4号线(火车站-车场)作为接运轨道交通进行实证分析, 长春轻轨4号线及周边公交线路情况见图1。
长春四环以内道路交通顺畅, 为简便运算, 四环以外有效路径参数φ 视为0, 即居民选择最短路出行。利用TransCAD构造长春市道路网络, 利用随机用户平衡法将高峰时段全方式OD客流矩阵分配到路网中, 得到各路段运行时间作为路段阻抗, 以带权重的有效路径作为阻抗搜索所有节点的最短有效路径, 计算参数φ 取不同值时的网络效率Ef和平均出行时间 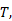
运用已有研究对原有公交线路优化, 基于最优φ 值通过获得高峰时段接运客流OD矩阵进行线路搜索, 获得符合模型目标及约束条件的接运线路, 由此得到基于有效路径的新增接运公交线网如图3所示。
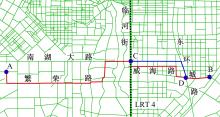
图3中接运公交为新增线路, 由图1可知长春市城区内线路较为成熟, 原有公交线路可起到接运中心城区客流的作用。剔除已有线路可运送的客流后得到的OD矩阵主要为满足城区外围至市中心的客流需求, 接运线路布设主要满足北部及南部新建区域客流需求, 是对原有公交网络的一种有效补充。由于受场地限制, 部分接运线路首末站不位于轨道交通站处, 而是选择现有线路首末站或城市外围节点作为首末站, 验证了备选线路中组合线路的可行性。选取某一接运线路说明所定义的有效路径对接运线路布设的影响, 如图4所示。
图4中“ A-C-D-B” 为接运公交线路, C为接运站点, 其中C-D段“ 南湖大路-东环城路” 路段为基于最短路布设的线路路径, “ 威海路” 路段为考虑有效路径所布设的线路路径, 上述两种情况下的公交线路分别定义为route1和route2。参数φ 取值为0和0.08时各线路运行参数如表1所示。
| 表1 不同φ 值下的接运线路运行参数 Table 1 Feeder bus operating parameters with φ |
由表1可知, 考虑最短路布设的公交线路长度低于基于有效路径布设的公交线路长度; 当φ =0时, route1的运行时间低于route2, 运送速度高于route2, 主要由于在不考虑拥堵情况下, 南湖大路的通行能力及设计通行速度高于威海路; 当φ =0.08时, route1的运行时间高于route2, 运送速度也急剧下降, 主要由于南湖大路及东环城路部分路段介数明显高于威海路路段介数, 造成路段有效权重较大, 即可认为这些路段发生拥堵的概率高于威海路, 因此计算出的有效路径长度高于威海路, 线路避开易发生拥堵的南湖大路和东环城路而选择途经威海路可以有效降低乘客出行成本, 线路布设更能体现居民实际出行策略。
运用复杂网络理论介数概念, 引入参数 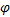
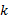
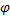
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|



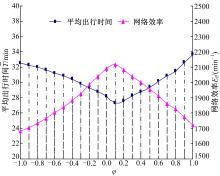
 随φ 变化趋势图
随φ 变化趋势图 with φ
with φ