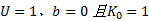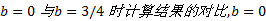朱福(1981-),男,实验师,博士研究生.研究方向:路基路面与岩土工程.E-mail: zhufu_1981@163.com
基于统一强度理论,考虑软土地基固结、中间主应力、静止侧压力系数对地基承载力的影响,推导出软土地基承载力计算公式,并应用于软土地区铁路路基填筑高度计算中,提出一种路堤临界填筑高度计算方法。用铁路工程路基填筑实例进行了验证,计算结果与工程试验结果吻合较好,可以为推算各阶段软土地区铁路工程路基填筑安全高度提供参考。
A new theoretical formula for soft ground bearing capacity is derived. This formula is based the unified strength theory, and the effects of consolidation, intermediate principal stress and the coefficient of lateral pressure are taken into consideration. According to this formula, an improved calculation method of the critical filling height of embankment is proposed. In addition, the calculation method is applied to railway subgrade filling test data to check its feasibility. The calculated results show reasonable good agreement with experiment results. The new formula may be used as the theoretical basis for determining the safe filling height at different phases of railway subgrade works.
在软土地区道路工程建设中, 路堤填筑高度是设计、施工与监理常遇到的问题。路堤填高的确定直接影响路基工程投资、施工进度, 此问题备受关注。国外学者Leroueil等[1, 2]进行了路堤填筑过程中软土地基的超静孔隙水压力和侧向变形的增长规律的研究, 分析了地基土屈服前后变形机理, 得出了基于变形控制的路堤临界填筑高度计算方法。Zdravkovic等[3]通过建立各向异性有限元模型, 分析了土体的各向异性对软土地基上路堤填筑高度的影响, 得出忽略土体的各向异性或凭借经验简单处理, 增加工程风险显著的结论。McGuire[4]研究了路堤荷载作用下桩处理后地基的变形特征, 提出了一系列不同桩径与空间排列方式下的路堤临界填筑高度。国内学者王铁行等[5]开展了多年冻土路堤临界高度的研究, 邓永锋等[6]开展了高速公路工程中动态临界填筑高度的应用研究, 江国勤等[7]分析了天然软土地基上路堤临界高度, 朱福等[8]提出了公路工程一种路堤临界高度计算方法。目前, 基于Mohr-Coulomb强度理论得出的地基承载力公式没有考虑中间主应力对强度的影响。俞茂宏[9]提出统一强度理论后, 一些学者把统一强度理论引入地基承载力计算中, 分析了中间主应力对地基承载力的影响作用, 拓宽了其应用范围。例如, 范文等[10]推导出基于统一强度理论的地基承载力公式; 王祥秋等[11]基于统一强度理论, 推导出了条形受荷地基承载力的计算公式。
综上所述, 国内外关于路堤填筑高度理论计算方法的研究较少, 考虑中间主应力对地基承载力与路堤临界填筑高度影响的研究更少。关于中间主应力、静止侧压力系数、软土地基固结对地基承载力与路堤填筑高度的综合影响的理论计算方法研究未见涉及, 为此, 本文在已有研究[8]基础上, 依据等代荷载法对路堤荷载进行了简化, 基于统一强度理论, 考虑软土地基固结、中间主应力、静止侧压力系数的效应, 推导出软土地基承载力计算公式, 进而提出一种改进的路堤临界填筑高度计算方法。
采用 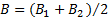
(1)任意一点 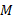
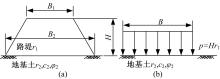
如图2(a)所示, 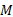

式中: r2 为路堤下地基土的重度; z为M点至地基顶面距离; K0为软土地基中土体的静止侧压力系数。
(2)任意一点 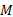
由文献[12]可知:弗拉曼推得的极坐标系下均布线性荷载作用下均质地基土中附加应力表达式为:
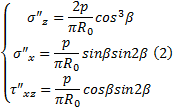
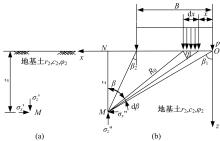
在极坐标系下, 如图2(b)所示, 从 M点到荷载边缘的连线与竖直线之间的夹角分别表示为β 1 与β 2, 其正负号规定为从竖直线MN绕M点顺时针旋转至连线时取正值, 反之取负值。因此, 图2(b)中的 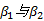
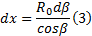
把式(3)代入式(2), 在荷载分布宽度 B范围内进行积分, 由此得到均布荷载p作用下M点的附加应力σ ″z表达为:
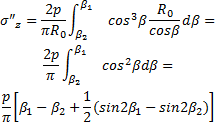
利用和差化积公式整理上式可得 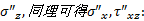
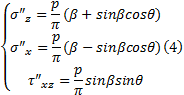
式中: 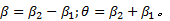
(3)任意一点 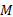
联立式(1)(4)可得 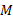
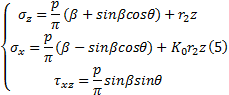
(1)任意一点 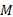
材料力学中关于主应力、法向应力、剪应力的关系式如下:
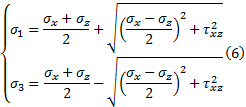
路堤中心线下应力最大, 将先达到屈服而破坏[8]。为便于推导, 仅考虑路堤中心线下地基土中应力计算(偏于安全)。由图2(b)中的几何关系与对称性得知: 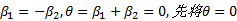
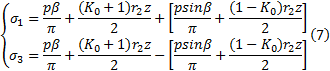
(2)任意一点 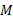
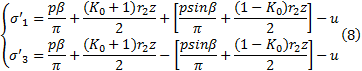
式中: 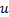
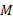
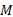
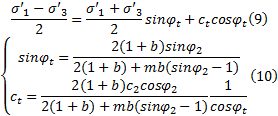
式中: b为统一强度理论参数; m为中间主应力参数^[13] ; c2 为黏聚力; φ 2 为内摩擦角; ct 为统一黏聚力; φ t为统一内摩擦角。
联立式(8)(9)得到塑性区的边界方程为:
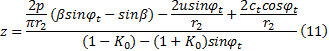
将式(11)对 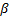
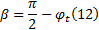
联立式(12)与式(11), 整理出塑性区最大开展深度zmax表达式为:
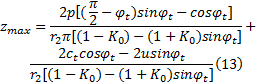
由土力学理论可知[12], 附加应力 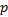
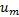
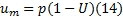
式中: 
采用 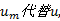
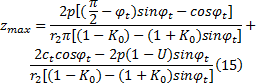
当zmax=0时, 可得软土地基临塑荷载pcr:
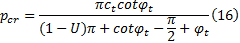
实际工程中, 经常以地基土体中出现一定深度的塑性区作为破坏准则[8, 12], 故取 zmax=B/4, 得软土地基临界荷载p1⁄4表达式为:
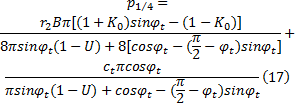
将 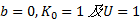
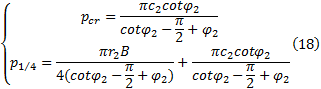
设路堤临界高度为 HB/4, 路堤填筑材料平均重度为r1, 则存在如下关系式:
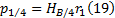
将式(17)代入式(19)整理后得:
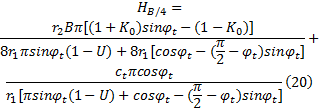
某铁路路基工程[14], 路堤顶宽度B1=10.8 m, 基底宽度B2=21.6 m, 路堤填土的重度为γ 1=17.5 kN/m3, 路堤填高至3.5~4.0 m发生坍滑。地基为软黏土, 地下水位与地面齐平, 地基土重度为γ 2=17.6 kN/m3, 三轴固结快剪测定得黏聚力c2=8 kPa, φ 2=13.5° 。
关于静止侧压力系数 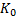
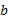
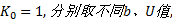
| 表1 不同b和U时临界荷载与路堤临界填高 Table 1 Calculation results of critical load and filling height of embankment of different values of b and U |
将表1数据与文献[14]中数据对比发现, 当b=3/4时, 本文的软土地基承载力及路堤临界填高的计算结果与文献[14]计算结果很接近。比较结果见表2。
| 表2 计算结果比较 Table 2 Comparison of calculation results |
(1)基于统一强度理论, 考虑软土地基固结、中间主应力、静止侧压力系数对软土地基承载力的影响, 进行了承载力计算公式的推求, 将推导的公式应用于铁路工程路基填高计算中, 提出一种改进的路堤临界填筑高度理论计算方法。
(2)推导的公式可以计算出不同固结度下的软土地基承载力和路堤填筑高度, 从而了解路基填筑施工过程中软土地基承载力的变化, 用以控制路基填筑时间与高度。
(3)将推导的理论公式应用于软土地区路基工程, 并与已有文献研究成果进行了对比, 验证了计算方法的可行性。
(4)软土地基因固结, 承载能力逐渐提高, 不仅发生在路基填筑阶段, 还会发生在施工后, 采用文中公式计算路堤填筑高度, 沉降是否会满足要求, 还需要进一步研究。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|