苏迎社(1963-),男,高级工程师,硕士生导师.研究方向:建筑工程设计.E-mail:2664482308@qq.com
在以往关于土拱效应研究的基础上,提出了土拱荷载传递比的概念,并建立了分析计算模型。通过土工离心机模型试验验证了Ito提出的排桩桩侧土压力的计算方法在深基坑疏排桩支护结构中的适用性,并基于该方法,结合一个疏排桩支护工程事例对土拱荷载传递比的影响因素作了比较全面的分析。研究结果表明:疏排桩支护结构中,桩间土拱效应不容忽视,通过土拱传递到排桩上的土压力最大可占到排桩承受的总土压力的60%以上;土拱荷载传递比随着桩间净距的增大近似呈指数形式减小,当桩间距相同时,桩径越大,土拱荷载传递比越小;当其他参数不变时,土拱荷载传递比随土体内摩擦角和土体黏聚力的增加近似呈指数形式增加。
Base on previous research on soil arching effect between adjacent piles, the concept of load transfer ratio of soil arching was proposed, and an analysis model was established. Through centrifuge model test, the Ito's calculation method of lateral pressure on pile was proved to be applicable to deep foundation supported with sparse row piles. Based on this approach, the influence factor of the load transfer ratio of soil arching was comprehensively analyzed with an assumed case of sparse row piles. Results show that the earth pressure passing to the pile by soil arching can account for over 60% of the total pressure on the pile. Therefore, soil arching effect between adjacent piles in sparse row pile retaining structure can not be ignored. The load transfer ratio of soil arching approximately exponentially decreases with the increase in pile space. When the pile space is constant the load transfer ratio decreases with the increase in pile diameter. In addition, if parameters are unchanged, the load transfer ratio exponentially increases with the cohesion and internal friction angle of the soil.
土拱现象最早是由Terzaghi于1943年的基于活动门试验[1]提出, 随后, Ladanyi[2], Wang[3]and Chen[4, 5]等先后通过理论、试验和数值模拟验证了桩间土拱效应的存在, 定性地分析了土拱的存在条件和土体参数对土拱效应的影响。
土拱效应是由于桩后土体发生不均匀位移而产生应力重新分布和传递的现象。作者通过阅读大量现有文献发现, 现有文献中研究较多的是土拱效应的存在条件和影响因素, 如极限桩间距研究[6, 7, 8, 9], 而对于排桩受到的桩侧土压力究竟有多少是通过土拱传递到排桩上的定量分析很少。基于此, 本文首先提出了土拱荷载传递比的概念, 并建立了土拱荷载传递比的计算模型; 然后基于离心机模型试验验证了Ito[10]提出的基于土塑性力学计算桩侧土压力方法对于深基坑疏排桩支护结构中的适用性; 最后通过一个工程事例基于Ito方法结合本文计算模型对疏排桩中土拱荷载传递比的影响因素进行了比较全面的分析。
对于疏排桩, 支护结构受到的土压力由于土拱作用引起重分布, 考虑土拱效应可将排桩支护结构分为4个区域, 如图1所示。
 | 图1 考虑土拱效应的排桩支护结构俯视图Fig.1 Top view of pile retaining structure considering the effect of soil arching |
图中, Ⅰ 区为拱前自由土体区; Ⅱ 区为土拱作用区; Ⅲ 区为拱后滑移土体区; Ⅳ 区为桩后土体区。设Ⅰ 区土体产生的土压力为 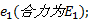

定义土拱效应荷载传递比λ 为经土拱传递到排桩上的土压力与排桩受到的总土压力之比:
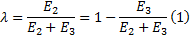
由于 E3 等于主动土压力Ea, 可通过朗肯主动土压力理论或者库伦主动土压力理论求出, 因此只要求出排桩上作用的总土压力(E2+E3), 即可求出土拱效应荷载传递比λ 。Ito和Matsui[10]曾将土和桩分别作为Mohor-Coulomb材料和刚性体, 考虑软弱土体从排桩间产生挤出的塑性变形, 利用土的塑性理论建立了位于边坡中排桩承受边坡滑动时的极限侧向土压力, 并利用室内模型试验进行了验证[10, 11]。本文利用Ito和Matsui的研究成果, 将其应用于疏排桩支护结构中土拱效应荷载传递比的分析。Ito和Matsui所提出的作用于排桩上的侧向土压力计算公式为:

式中: 




求出排桩桩侧总土压力后代入式(1)即可求出土拱效应荷载传递比 
古海东[12]通过离心机模型试验给出了疏排桩支护结构桩身内力与桩侧土压力的分布规律。试验用土取自上海杨浦区五角场的砂质粉土, 该土样的级配曲线如图2所示。
通过击实试验得到该土样的最优含水率为18%, 最大干密度为1.53 g/cm3, 对应的密度为1.8 g/cm3, 本次离心机试验制备含水率为18%的非饱和土, 土样的物理力学性质如下:比重为2.7, 含水量为18%, 密度为1.8 g/cm3, 固结不排水强度c=23 kPa, φ =34° 。在1g(g为重力加速度)状态下, 在净空为700 mm× 440 mm× 700 mm(高)的模型箱中完成模型制备。
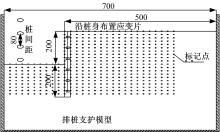
在填土前, 模型箱两侧用凡士林粘贴双层聚四氟乙烯薄膜以减小侧壁摩擦。模型中桩采用外径为20 mm, 内径14 mm的铝管, 桩内壁布置弯曲应变片, 桩表面打磨后外径为18 mm, 桩长为400 mm, 杨氏模量为70 GPa, 填土时将排桩预先埋入土中。整个支护结构模型简图见图3。
将制备好的离心机模型调入离心机吊篮进行模型固结试验(模型比例尺为60), 试验开始后离心加速度以10g为一级, 每级加速度下运转3 min, 最后在60g的离心加速度下运转36 min(相当于实际工程中的3个月), 固结完成的判断标准为模型地表沉降趋于稳定(因土样含水率较低, 无法通过空隙水压力传感器读数来判断固结是否完成)。固结结束后将模型箱调出, 开挖成高度为200 mm, 坡角为90° 的竖直基坑, 拆开模型箱侧壁, 在模型基坑侧面用长度为1 mm的彩色大头针布置标记点, 如图3所示。标记点布置完毕后重新组装模型箱, 然后将模型箱吊入离心机吊篮, 待模型箱中的位移传感器、土压力盒以及桩身应变片等接线通道调试完毕后, 开启离心机, 先在10g加速度下运转3 min, 观看离心机是否运转正常, 一切正常后从30g离心加速度开始以每5g为一级, 每级加速度下运转15 min, 如果模型在这一级加速度下破坏, 或者在期间的任意加速度下破坏, 试验即告结束。
离心机试验结果:基坑在离心加速度为55g时桩间土体发生塌落破坏, 塌落后桩间土体近似成土拱形, 最大拱高约为30 mm, 塌落后的支护结构如图4所示。
试验得出在不同离心加速度下疏排桩桩身弯矩、水平位移如图5所示。
 | 图5 不同离心加速度下的桩身弯矩和水平位移分布Fig.5 Bending moment and horizontal displacement distribution of pile under different centrifugal acceleration |
图6为根据Ito[10]计算方法编制MATLAB程序计算得出的本文离心机模型中不同离心加速度下的桩侧土压力和离心模型试验得出的桩侧土压力的对比曲线图。
由图6可知, 在基坑坑壁处采用Ito计算方法得到的桩侧土压力分布和离心机试验结果基本一致, 说明采用Ito计算方法计算基坑坑壁处的桩侧土压力是完全可行的。
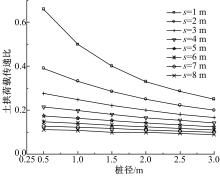
假定一疏排桩基坑支护工程事例, 基坑开挖深度为8 m, 桩长为16 m, 土层参数与上文保持一致, 分别取桩径 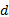
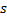
由图7可知:土拱荷载传递比随着桩间净距的增大整体上呈指数形式减小, 但是当排桩桩间净距为0时, 土拱荷载传递比为0, 说明密排桩时土拱效应不存在; 当桩间净距超过6 m以后, 土拱荷载传递比非常小(只有0.1左右), 说明当桩间距较大时土拱效应非常微弱, 土拱的存在有一个极限桩间距; 当桩间距相同时, 桩径越大, 土拱荷载传递比越小。
分别取排桩净间距 

由图8可知:土拱荷载传递比随着桩径的增大而减小, 桩间净距越小, 桩径对土拱荷载传递比影响越显著。
3.3.1土体内摩擦角的影响
取桩径为d=1 m, 桩间净距s=1 m, 土体黏聚力c=23 kPa保持不变, 依次取土体内摩擦角 
 | 图9 土体内摩擦角对土拱荷载传递比的影响Fig.9 Influence of internal friction angel of soil on load transfer ratio of soil arching |
由图9可知:当其他参数不变时, 土拱荷载传递比随土体内摩擦角的增大近似成指数形式增大, 随着土体内摩擦角的增加, 土拱荷载传递比增大的趋势越来越缓慢。
3.3.2 土体黏聚力的影响
取d=1 m, s=1 m, φ =20° 保持不变, 依次取土体黏聚力为0、5、10、15、20、25、30 kPa, 研究土体黏聚力对土拱荷载传递比的影响, 如图10所示。
由图10可知:当其他参数不变时, 土拱荷载传递比随土体黏聚力的增大近似成指数形式增大, 并且增大的趋势越来越缓慢。
(1)疏排桩支护结构中, 土拱效应不容忽视, 通过土拱传递到排桩上的土压力最大可占到排桩承受的总土压力的60%以上。
(2)密排桩时土拱效应不存在; 疏排桩土拱荷载传递比随着桩间净距的增大近似呈指数形式减小, 当桩间净距超过6 m以后, 土拱荷载传递比非常小(只有0.1左右), 说明当桩间距较大时土拱效应非常微弱, 土拱的存在有一个极限桩间距; 当桩间距相同时, 桩径越大, 土拱荷载传递比越小。
(3)当其他参数不变时, 土拱荷载传递比随土体内摩擦角和土体黏聚力的增大近似成指数形式增大, 并且增大的趋势越来越缓慢。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|