引用本文
李海锋, 郭小农, 罗永峰, 高轩能. 索支撑柔性摩天轮结构抗倒塌性能分析. 45(2): 406-413
LI Hai-feng, GUO Xiao-nong, LUO Yong-feng, GAO Xuan-neng. Collapse resistance behavior of Ferris wheel with stay cables. Journal of Jilin University Engineering and Technology Edition, 45(2): 406-413  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
索支撑柔性摩天轮结构抗倒塌性能分析
李海锋1,2, 郭小农3, 罗永峰3, 高轩能1
1.华侨大学 土木工程学院,福建 厦门 361021
2.福建省结构工程与防灾重点实验室,福建 厦门 361021
3.同济大学 建筑工程系,上海 200092

李海锋(1983-),男,讲师,博士.研究方向:大跨空间结构抗震性能.E-mail:lihai_feng@126.com

基金:国家自然科学基金项目(51278208)。福建省教育厅科研项目(JA13015)
摘要

研究了稳定索以某种模式失效时摩天轮结构的动力响应,考察是否会引起其他稳定索的连续失效,导致结构丧失侧向刚度而倒塌。通过动力分析得出,结构侧向位移和索力变化周期与该摩天轮结构的第一阶自振周期 T1相近,且稳定索失效后0.5 T1时,索回弹动力效应对摩天轮结构的影响最显著;稳定索在失效模式FM3-1(单侧3根稳定索失效)下,索回弹动力效应对摩天轮结构影响最大,且一侧稳定索最大索力达到64%的破断力,另一侧稳定索几乎处于松弛状态;在任一稳定索失效模式下,都不会造成其他稳定索的破断继而发生连续性破坏,此类大型柔性摩天轮结构具有抗倒塌性能。

关键词: 土木建筑结构; 摩天轮; 稳定索失效; 动力分析; 倒塌
中图分类号:TU391 文献标志码:A 文章编号:1671-5497(2015)02-0406-08
Collapse resistance behavior of Ferris wheel with stay cables
LI Hai-feng1,2, GUO Xiao-nong3, LUO Yong-feng3, GAO Xuan-neng1
1.College of Civil Engineering, Huaqiao University, Xiamen 361021, China
2.Key Laboratory for Structure Engineering and Disaster Prevention of Fujian Province,Xiamen 361021,China
3.Departments of Building Engineering, Tongji University, Shanghai 200092, China
Abstract

The dynamic responses of an actual Ferris wheel system induced by failure of some stay cables are investigated. Whether the failure of some stay cables can cause further failure of other stay cables, or lost of the lateral stiffness of the wheel, even collapse is discussed. Constructive results are obtained by means of dynamic analysis. The variation periods of the lateral displacement of the wheel and the stay cable force are almost equal to the first natural vibration period ( Tl) of the wheel. It is about half of Tl after the failure of the stay cables, the effect of the resilience of the failure stay cables on the dynamic behavior of the wheel becomes obvious and reach to an upper limit. The predominant failure model is the failure of three stay cables in one side at the same time. In this situation, the maximal tension force of the stay cables laying in one side reaches 64% of it breaking force; while the stay cables laying in the other side are almost in slack state. In conclusion, any specific failure mode of the stay cables would not cause the further failure of other stay cables, which might result in collapse of the wheel. Numerical results show that the collapse resistance of the Ferris wheel is strong enough.

Keyword: civil engineering structure; Ferris wheel; failure of stay cables; dynamic analysis; collapse
引言

摩天轮结构[1, 2]主要由轮盘系统和支撑系统两部分组成。轮盘结构类似于自行车轮, 轮缘常采用刚性桁架结构体系, 轮辐为柔性索体系, 通过对轮辐索施加预应力使轮盘结构成形并具有所需要的刚度。轮盘系统的荷载通过轴套传给由支架柱、芯轴系统和稳定索组成的支撑系统, 所有竖向荷载最终由支架柱传给基础。支架柱、芯轴系统和稳定索组成了摩天轮结构的抗倒塌体系。摩天轮结构主要依靠稳定索来保证支架系统的侧向稳定, 而稳定索索力的大小将直接影响摩天轮结构的侧向刚度, 计算表明, 当稳定索的预拉力达到索破断强度的20%~30%时, 摩天轮结构才具有足够的侧向刚度。若某一根稳定索突然失效, 摩天轮结构将承受稳定索回弹力的动力作用, 在此动力作用过程中, 有可能引起其他稳定索的超载并达到破断强度而破坏, 继而使摩天轮结构承受更大的索回弹力的动力作用。当摩天轮支撑系统一侧的稳定索全部失效时, 摩天轮结构将变为可变体系, 发生倒塌破坏。

随着美国911恐怖袭击中世贸大楼的倒塌, 各国对建筑结构的抗倒塌性能[3, 4, 5, 6]更为重视, 并进行了深入的研究。但国内外对摩天轮结构稳定索突然断裂可能引发整个结构倒塌破坏问题的研究鲜有涉及。本文研究大型柔性摩天轮结构的稳定索以某种可能的模式失效时结构的动力响应, 并考察是否会引起其他稳定索的连续性失效或破断, 进而研究导致摩天轮结构丧失侧向刚度的失效模式, 为摩天轮结构稳定索突然断裂的动力问题提供可靠的分析方法。本文研究内容和结果可为此类大型柔性摩天轮结构的设计分析提供必要的技术资料和设计依据。

1 分析模型

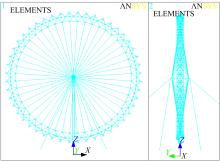
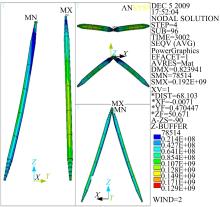
本文分析的摩天轮轮盘直径为183 m, 总高为208 m, 其结构系统由支架、稳定索、芯轴、轮盘系统组成。支架柱由4根双向倾斜的巨型圆管立柱组成, 单根立柱长约115 m。支架两侧各设置4根斜拉的稳定索, 每根索长约170 m, 初始预拉力为3000 kN, 最小破断力为12 795 kN, 两端分别固定于支架顶部和地面锚墩上。芯轴高度为108.25 m, 支承于支架柱顶。轮辐索48根, 每根索长约90 m, 初始预拉力为3300 kN。轮缘为呈倒三角形的桁架。采用ANSYS软件建立结构分析模型, 有限元模型如图1所示。

图1 ANSYS单元模型Fig.1 Diagram of ANSYS element model

采用瞬态动力分析方法[7]研究摩天轮结构在稳定索回弹力作用下的动力响应, 该分析方法采用完整的系统矩阵计算瞬态响应, 可考虑塑性、大变形等各类非线性[8, 9, 10]特性。瞬态分析的关键问题为积分时间步长选取、荷载步划分、初始条件确定以及阻尼设置。具体计算方法如下:

(1)积分时间步长选取

积分时间步长 不仅影响计算效率, 而且影响瞬态分析的精度和收敛性。结构动力响应为各阶模态响应的组合, 的设置应能够使计算结果包含对结构整体响应有较大贡献的最高阶模态。设 为对结构整体响应有较大贡献的最高阶频率, 则积分时间步长应满足 经数值分析可知, 本文计算模型中对结构整体响应有显著贡献的最高阶频率为0.9665 Hz, 综合考虑计算精度和计算效率, 本文选取的积分时间步长 为0.02 s。

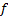
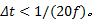
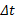
(2)荷载步划分

在瞬态动力分析中, 荷载随时间变化, 即荷载是时间的函数, 必须将荷载-时间关系划分为合适的荷载步。为了更加真实地模拟摩天轮结构在稳定索失效时的动力响应过程, 本文第一个荷载步为对轮辐索和稳定索施加相应的预应力以形成正常结构体系, 第二个荷载步为施加重力荷载, 第三个荷载步为施加风荷载等外荷载, 第四个荷载步为稳定索回弹力的动力荷载步。

(3)初始条件确定

结构体系的动力学方程为:

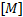
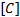
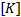
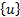
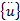
式中: 为质量矩阵; 为阻尼矩阵; 为刚度矩阵; 为节点位移向量; 为节点加速度向量; 为节点速度向量; 为节点荷载向量。

式(1)的求解需要两个初始条件, 即初始位移和初始速度。本文摩天轮结构的初始位移是由第三个荷载步求得的位移。初始速度为零, 是通过调整前三个荷载步作用的时间远远大于积分时间步长得到的。

(4)阻尼设置

阻尼机理[11, 12]非常复杂, 它与结构周围介质的黏性、结构本身的黏性、内摩擦耗能、地基土的能量耗散等有关。在计算分析时常采用瑞利(Rayleigh)阻尼, 即:

式中: 为质量阻尼系数; 为刚度阻尼系数。这两个阻尼系数可通过振型阻尼比计算得到, 即:

式中: 和 分别为结构的第 和第 阶固有圆频率; 和 分别为相应于第 和第 阶振型的阻尼比。

2 稳定索失效模式

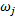
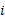
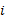
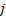
本文分析模型中稳定索的编号如图2所示, 其中1~4号索为左侧稳定索, 5~8号索为右侧稳定索。

图2 稳定索编号Fig.2 The number of stay cables

考虑垂直于轮面方向的不利荷载影响, 选取对稳定索最不利的荷载工况 (1.2┤DL+1.2PS+1.4WL)+FM进行分析, 其中DL为恒载, PS为索预拉力, WL为风荷载, FM为失效索的动力回弹作用。由于该摩天轮结构为对称结构形式, 风荷载WL仅取沿 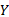轴正向的风荷载。

为研究摩天轮结构的抗倒塌性能, 本文选择多种稳定索失效模式进行数值分析。当风荷载沿 轴正向作用时, 左侧稳定索失效对摩天轮结构最不利。在设计稳定索失效模式时, 尽可能选择左侧稳定索失效的模式, 同时利用结构的对称性减少稳定索失效模式的数量。本文设计的稳定索失效模式如表1所示。

表1 稳定索失效模式 Table 1 Failure modes of stay cables
3 稳定索失效后结构的动力响应

为研究摩天轮结构的稳定索突然断裂是否会引起整个结构倒塌破坏, 本文详细分析了在失效稳定索回弹力的动力荷载作用下, 摩天轮结构侧向位移、未失效稳定索索力、支架柱受力状态的变化规律, 进而对摩天轮结构的抗倒塌性能进行评定。

3.1 结构侧向位移的变化规律

本文仅给出表1中典型失效模式FM1-1、FM2-1、FM2-5、FM3-1、FM3-3、FM4-1、FM4-2、FM5、FM6下摩天轮支架柱顶位置侧向位移 的变化规律, 如图3所示。

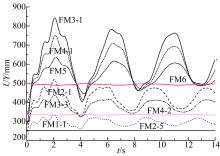图3 典型失效模式下支架柱顶位置侧向位移的变化规律Fig.3 Lateral displacement of the wheel structure nduced by some typical stay cables

分析摩天轮结构侧向位移的变化规律(图3)可得:

(1)在稳定索失效模式FM2-5、FM4-2、FM6下, 摩天轮支架柱顶位置侧向位移的动力响应均接近水平直线变化, 且稳定索失效越多, 结构的侧向位移越大。表明两侧失效稳定索数相同时, 索回弹力的动力效应相互抵消, 且稳定索失效越多, 结构的侧向刚度退化越严重。

(2)对该摩天轮结构进行固有自振特性分析后, 得出该摩天轮结构的第一阶自振周期T1为3.74 s。由图3可知, 结构侧向位移变化曲线的周期约为4 s, 与该摩天轮结构的第一阶自振周期相近。稳定索失效后2 s, 结构的侧向位移最大, 由于阻尼的作用, 结构侧向位移变化曲线的波峰随时间不断减小。表明稳定索失效后0.5T1时, 索回弹动力效应对摩天轮结构的影响最大。

为进一步比较稳定索失效模式对摩天轮结构的影响以及瞬态动力分析方法与普通静力求解方法的差别, 表2给出了各稳定索失效模式下两种方法所得的支架柱顶位置结构的最大侧移值。其中, 静力求解方法仅是将失效的稳定索从整体模型中除去后重新进行静力求解, 并未考虑失效稳定索回弹力的动力效应。动力放大系数的计算式为:

分析表2可得:

(1)稳定索失效模式FM3-1下, 支架柱顶位置结构的最大侧移值和动力放大系数均最大。表明在该失效模式下摩天轮结构的侧向刚度最小, 且失效稳定索的回弹力动力效应对结构的影响也最大。

(2)稳定索失效模式FM2-5下, 支架柱顶位置结构的最大侧移值和动力放大系数均最小。表明在该失效模式下失效稳定索的回弹力动力效应对结构的影响最小。

(3)当不同失效模式一侧失效的稳定索数相同时, 支架柱顶位置结构的最大侧移值相差不大, 表明同侧稳定索失效位置的变化对摩天轮结构的影响相对较小。

表2 支架柱顶位置结构的最大侧移值 Table 2 Largest lateral displacement of the wheel structure at the top of the column
3.2 未失效稳定索索力的变化规律

为考察稳定索以某种模式突然失效时, 摩天轮结构在失效稳定索回弹力的动力荷载作用下是否会引起其他稳定索的超载并达到破断强度而破坏, 本文重点分析了未失效稳定索索力的变化规律, 并与破断强度进行比较, 以判断其是否达到破断强度而破坏。

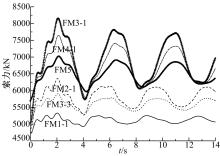
图4为典型失效模式FM1-1、FM2-1、FM3-1、FM3-3、FM4-1、FM5下左侧未失效稳定索索力的变化规律。各失效模式下左侧未失效稳定索的最大索力值列于表3。

图4 左侧未失效稳定索索力的变化规律Fig.4 Force responses of stay cables on the left side

表3 左侧未失效稳定索的最大索力 Table 3 Largest forces of stay cables on the left side

分析图4和表3可得:

(1)典型稳定索失效模式下, 左侧未失效稳定索索力增大, 且索力的变化规律与结构侧向位移的变化规律一致。即左侧未失效稳定索索力变化曲线的周期约为4 s, 与摩天轮结构的第一阶自振周期T1相近; 稳定索失效后0.5T1时, 左侧未失效稳定索的索力达到最大值, 且索力变化曲线的波峰随时间不断减小。

(2)在同一稳定索失效模式下, 左侧各根未失效稳定索的最大索力值几乎相等, 且索力的变化规律一致。

(3)稳定索失效模式FM3-1下, 左侧未失效稳定索索力增加最多, 索力最大值为8155 kN, 达到64%的破断力。表明该摩天轮结构在任一稳定索失效模式下均不会引起其他稳定索的连续性失效或破断, 该摩天轮结构具有抗倒塌性能。

(4)比较表2、表3中的动力放大系数可知:结构侧向位移的最大动力放大系数为37.84%, 而未失效稳定索索力的最大动力放大系数仅为18.6%。表明摩天轮结构的侧向位移对失效稳定索回弹力的动力效应更为敏感。

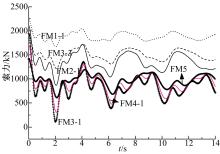
图5为典型失效模式FM1-1、FM2-1、FM3-1、FM3-3、FM4-1、FM5下右侧未失效稳定索索力的变化规律。各失效模式下右侧未失效稳定索的最小索力值列于表4。其中, 偏差的计算式为:

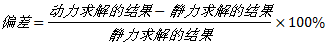
图5 右侧未失效稳定索索力的变化规律Fig.5 Force responses of stay cables on the right side

分析图5和表4可得:

(1)稳定索失效后, 右侧未失效稳定索索力将减小, 以致失效索回弹动力效应对右侧未失效索索力的影响较为显著, 其动力求解和静力求解的最大偏差高达87.2%。

(2)失效索回弹动力作用效应越大, 右侧未失效稳定索索力变化曲线越呈高频变化的趋势; 而失效索回弹动力作用效应越小, 右侧未失效稳定索索力的变化规律与结构侧向位移的变化规律越接近。

(3)在同一稳定索失效模式下, 右侧各根未失效稳定索的最小索力值几乎相等, 且索力的变化规律也基本一致。

(4)在稳定索失效模式FM3-1下, 右侧未失效稳定索索力最小, 仅为104 kN, 几乎处于松弛状态。

表4 右侧未失效稳定索的最小索力 Table 4 Smallest forces of stay cables on the right side
3.3 稳定索失效对支架柱的影响

摩天轮结构的竖向荷载最终均由支架柱传给基础, 支架柱的受力状态对摩天轮结构的抗倒塌性能影响较大。选取对摩天轮结构最不利的稳定索失效模式FM3-1作为分析工况。研究此稳定索失效模式下支架柱底反力及其应力分布的变化规律, 从而分析稳定索失效对支架柱的影响。

在稳定索失效模式FM3-1下, 柱底结点编号如图6所示, 支架柱底反力的变化规律如图7所示。表5给出了稳定索未失效计算模型和稳定索失效模式FM3-1下支架柱底的最大反力值及其差值。其中, 差值的计算式为:

图6 支架柱底结点编号Fig.6 Node number of the supporting column

分析图7和表5可得:稳定索失效模式FM3-1下右侧支架柱底反力增加, 而左侧支架柱底反力将减小。其中, 右侧44号结点位置处的支座反力增大最多, 达7.11%; 左侧43号结点位置处的支座反力减小最多, 达26.28%。总体来看, 失效稳定索回弹力的动力效应对支架柱的不利影响相对较小。

图7 支架柱底反力的变化规律Fig.7 Reaction force of the supporting column

表5 支架柱底最大反力值 Table 5 Largest reaction force of the supporting column

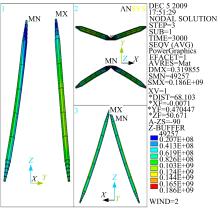
为进一步考察稳定索失效对支架柱的影响, 图8给出了稳定索未失效时支架柱的应力分布云图; 图9给出了稳定索失效模式FM3-1下支架柱应力最大时的应力分布云图。

图8 稳定索未失效时支架柱应力云图Fig.8 Stress distribution of the column in undamaged model

比较图8、图9可知:稳定索未失效时支架柱的最大应力为186 MPa, 在最不利的稳定索失效模式FM3-1下, 支架柱的最大应力仅增大到192 MPa, 支架柱仍处于弹性受力状态。表明失效稳定索回弹力的动力效应不会使支架柱发生破坏, 此类大型柔性摩天轮结构具有抗倒塌性能。

图9 FM3-1下支架柱应力最大时的应力云图Fig.9 Stress distribution of the column in FM3-1 model

4 结论

(1)两侧稳定索失效根数相同时, 索回弹力的动力效应相互抵消, 且稳定索失效越多, 结构的侧向刚度退化越严重。

(2)结构侧向位移和索力变化周期与该摩天轮结构的第一阶自振周期T1相近, 且稳定索失效后0.5T1时, 索回弹动力效应对摩天轮结构的影响最显著。

(3)稳定索失效模式FM3-1(单侧3根稳定索失效)下, 索回弹动力效应对摩天轮结构影响最大, 且一侧稳定索最大索力达到64%的破断力, 另一侧稳定索几乎处于松弛状态。

(4)失效稳定索回弹力的动力效应对支架柱的不利影响相对较小。

(5)在任一稳定索失效模式下, 都不会造成其他稳定索的破断继而发生连续性破坏, 此类大型柔性摩天轮结构具有抗倒塌性能。

The authors have declared that no competing interests exist.

参考文献
[1] 李海锋, 郭小农, 罗永峰, 等. 摩天轮结构的缺陷敏感性分析[J]. 结构工程师, 2010, 26(2): 24-30.
Li Hai-feng, Guo Xiao-nong, Luo Yong-feng, et al. Imperfection sensitivity analysis of ferris wheel structures[J]. Structural Engineers, 2010, 26(2): 24-30. [本文引用:1] [CJCR: 0.488]
[2] McNiven B, Dallard P. The singapore flyer and design of giant observation wheels[C]∥IStructE Asia-Pacific Forum on Structural Engineering: Innovations in Structural Engineering, Singapore, 2007: 2-3. [本文引用:1]
[3] Adam C, Jager C. Simplified collapse capacity assessment of earthquake excited regular frame structures vulnerable to P-delta[J]. Engineering Structures, 2012, 44: 159-173. [本文引用:1] [JCR: 1.713]
[4] 易伟建, 张凡榛. 钢筋混凝土板柱结构抗倒塌性能试验研究[J]. 建筑结构学报, 2012, 33(6): 35-41.
Yi Wei-jian, Zhang Fan-zhen. Experimental study on collapse performance of a RC flat plate frame structure[J]. Journal of Building Structures, 2012, 33(6): 35-41. [本文引用:1] [CJCR: 1.074]
[5] 张慎, 李霆, 杜新喜. 大跨空间网壳结构抗倒塌性能分析[J]. 建筑结构, 2010, 40(8): 22-26.
Zhang Shen, Li Ting, Du Xin-xi. Anti-collapse property analysis for long-span spatial latticed structures[J]. Building Structure, 2010, 40(8): 22-26. [本文引用:1] [CJCR: 0.5044]
[6] 李航, 马人乐, 陈俊岭. 河南省广播电视发射塔抗连续性倒塌分析[J]. 特种结构, 2008, 5(1): 40-43.
Li Hang, Ma Ren-le, Chen Jun-ling. Resisting progressive collapses ability of HeNan broadcast and television tower[J]. Special Structures, 2008, 5(1): 40-43. [本文引用:1] [CJCR: 0.1671]
[7] 王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007. [本文引用:1]
[8] 徐家初, 张勇. 爆炸冲击载荷作用下夹层开顶扁球壳的非线性动力稳定性分析[J]. 工程力学, 2011, 28(1): 150-156.
Xu Jia-chu, Zhang Yong. Nonlinear dynamic stability analysis of truncated sand wich shallow spherical shells subjected to explosive impacts[J]. Engineering Mechanics, 2011, 28(1): 150-156. [本文引用:1] [CJCR: 0.583]
[9] 林倩, 邓志恒, 刘其舟. 足尺钢桁架连梁抗震性能试验研究及非线性有限元分析[J]. 工程力学, 2012, 29(7): 256-263.
Lin Qian, Deng Zhi-heng, Liu Qi-zhou. Experimental study and nonlinear finite element analysis on the seismic performance of full-scale steel truss coupling beams[J]. Engineering Mechanics, 2012, 29(7): 256-263. [本文引用:1] [CJCR: 0.583]
[10] 陈常松, 苏龙, 颜东煌. 悬索桥索股架设全过程的非线性精确分析[J]. 西南交通大学学报, 2007, 42(1): 44-48.
Chen Chang-song, Su Long, Yan Dong-huang. Accurate nonlnear analysis of tower and cable in construction of main cable for suspension bridge[J]. Journal of Southwest Jiaotong University, 2007, 42(1): 44-48. [本文引用:1] [CJCR: 0.608]
[11] 焦常科, 李爱群, 王浩. 非线性阻尼动力方程的复合积分法[J]. 力学与实践, 2010, 32(4): 66-70.
Jiao Chang-ke, Li Ai-qun, Wang Hao. Composite implicit time integration method for dynamic equations with nonlinear damping[J]. Mechanics in Engineering, 2010, 32(4): 66-70. [本文引用:1] [CJCR: 0.235]
[12] 吕西林, 张杰. 钢和混凝土竖向混合结构阻尼特性研究[J]. 土木工程学报, 2012, 45(3): 10-16.
Lyu Xi-lin, Zhang Jie. Damping behavior of vertical structures with upper steel and lower concrete components[J]. China Civil Engineering Journal, 2012, 45(3): 10-16. [本文引用:1] [CJCR: 0.921]