引用本文
姜万录, 卢传奇, 朱勇. 基于HHT和模糊C均值聚类的轴向柱塞泵故障识别. 45(2): 429-436
JIANG Wan-lu, LU Chuan-qi, ZHU Yong. HHT and fuzzy C-means clustering-based fault recognition for axial piston pump. Journal of Jilin University Engineering and Technology Edition, 45(2): 429-436  
Permissions
Copyright©2015, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于HHT和模糊C均值聚类的轴向柱塞泵故障识别
姜万录1,2, 卢传奇1,2, 朱勇1,2
1.燕山大学 河北省重型机械流体动力传输与控制重点实验室,河北 秦皇岛 066004
2.燕山大学 先进锻压成形技术与科学教育部重点实验室,河北 秦皇岛 066004
朱勇(1986-),男,博士研究生.研究方向:故障信息诊断.E-mail:yzhu@ysu.edu.cn

姜万录(1964-),男,教授,博士生导师.研究方向:故障信息诊断.E-mail:wljiang@ysu.edu.cn

基金:国家自然科学基金项目(51475405).国家重点基础研究发展计划项目(2014CB046405).河北省自然科学基金项目(E2013203161)
摘要

提出了一种基于Hilbert-Huang变换(HHT)和模糊C均值聚类算法相结合的故障识别方法。利用HHT在处理非线性、非平稳信号方面的优势,对采集到的轴向柱塞泵泵壳振动加速度信号进行HHT处理。首先对信号分别进行经验模态分解(EMD)和集总经验模态分解(EEMD),结合短时最大熵谱分析选取对故障最为敏感的固有模态函数(IMF)分量,再对其分别进行二次分解。然后,采用本文提出的基于局部边际能量谱特征能量的方法求出故障特征向量。最后,采用模糊C均值聚类算法进行故障模式识别。识别结果表明:EEMD比EMD在迭代次数上大幅减少,故障识别准确率有了显著提高。

关键词: 流体传动与控制; 集总经验模态分解; 短时最大熵谱分析; 特征向量; 模糊C均值聚类
中图分类号:TH137 文献标志码:A 文章编号:1671-5497(2015)02-0429-08
HHT and fuzzy C-means clustering-based fault recognition for axial piston pump
JIANG Wan-lu1,2, LU Chuan-qi1,2, ZHU Yong1,2
1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control, Yanshan University, Qinhuangdao 066004, China
2.Key Laboratory of Advanced Forging & Stamping Technology and Science (Yanshan University), Ministry of Education of China, Qinhuangdao 066004, China
Abstract

A fault recognition method based on Hilbert-Huang Transform (HHT) and the fuzzy C-means clustering is proposed. This method takes advantages of HHT in processing nonlinear and non-stationary signals. The vibration acceleration signals collected from the axial piston pump housing are processed by HHT. First, the signals are treated by means of the Empirical Mode Decomposition (EMD) and the Ensemble Empirical Mode Decomposition (EEMD) respectively. Then, the Intrinsic Mode Function (IMF), which is most sensitive to faults, is chosen according to the short-term maximum entropy spectrum analysis, and the sensitive IMF is re-decomposed. Third, the fault characteristic vector is constructed based on the characteristic energy of the local marginal energy spectrum. Finally, the faults are recognized using the fuzzy C-means clustering algorithm. The results show that, compared with EMD, the interactive time based on EEMD is reduced greatly, and the fault recognition accuracy is substantially improved by the proposed recognition method.

Keyword: turn and control of fluid; ensemble empirical mode decomposition; short-term maximum entropy spectrum analysis; feature vector; fuzzy C-means clustering
引言

故障诊断实质上就是模式识别的过程, 包括故障敏感特征向量的提取和故障识别。与普通的旋转机械相比较, 轴向柱塞泵工作时既有旋转运动, 又有柱塞的往复直线运动, 传统的频谱分析对轴向柱塞泵的故障诊断效果不够理想, 因此如何找到敏感的故障特征就成了一个值得深入研究的问题。

希尔伯特-黄变换(Hilbert-Huang transform, HHT)是1998年由美国工程院院士黄锷首次提出[1], 由于在处理非线性、非平稳信号时有很好的效果, 目前在故障诊断领域得到了广泛应用。与传统的FFT相比, HHT把信号看成是由若干个固有模态分量(Intrinsic mode function, IMF)的叠加, 这些固有模态分量具有不同的特征尺度, 当轴向柱塞泵发生故障时, 这些特征尺度上的固有模态分量会发生变化, 有助于从中提取出敏感的故障特征。

研究发现, 通过对液压泵泵壳振动加速度信号进行HHT处理, 对选出的故障敏感固有模态分量进行Hilbert包络解调分析, 从频谱图中可以发现, 液压泵发生故障时, 多种故障的故障特征频率都与液压泵的转轴基频有关[2], 说明故障特征存在很强的相似性, 难以进行精确识别。研究表明[3], 一个发生故障的被诊系统, 其监测数据中往往包含各种复杂的模糊联系。采用模糊C均值聚类分析的方法, 先采集液压泵各种状态下的振动信号作为样本信号, 得到各种状态的标准模式, 然后加入待识别信号, 对它进行模糊C均值聚类分析, 根据模糊距离的分析与计算, 可以判别待诊状态以多大的隶属度属于某种故障, 从而识别故障。

本文提出一种基于HHT和模糊C均值聚类相结合的液压泵故障识别方法。首先对采集到的轴向柱塞泵的泵壳振动加速度信号分别进行经验模态分解(EMD)处理和集总经验模态分解(EEMD)处理, 得到一系列具有不同特征尺度的固有模态分量。通过短时最大熵谱[4]以及功率谱分析, 找到包含故障信息最丰富的分量, 然后再对其分别进行EMD和EEMD处理。按照基于局部边际能量谱[5]特征能量求取特征向量的方法, 分别求出经两种方法处理后的特征向量。最后, 采用模糊C均值聚类算法进行故障模式识别。

1 经验模态分解

HHT本质上是对信号进行平稳化处理, 就是对时间信号进行EMD处理。EMD处理后得到一系列IMF, IMF必须满足两个条件[6]:

(1)整个数据段上, 极值点的个数和过零点的次数必须相等或者相差最多不超过一个。

(2)任意时刻, 由局部极大值点形成的上包络线和局部极小值点形成的下包络线的平均值为零。

EMD本质上是一个筛分过程, 具体步骤如下:

对原始信号x(t), 如果它的上、下包络线的均值记为m1, 那么信号的第一个IMF可以按下式进行计算:

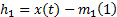
理想地, 如果h1满足IMF条件, 那么h1就是x(t)的第一个IMF。但是, 实际情况中往往需要多次重复筛分:

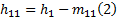
重复k次, 直到h1k满足IMF的条件:

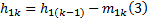
得到第一阶IMF, 记作c1:

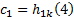
剩余信号记作r1:

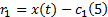
再将r1作为原始信号进行分解, 重复式(2)~(5), 可依次得到x(t)的n个满足条件的IMF分量:

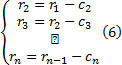
当分量cn或剩余量rn小于事先规定的一个阈值, 或者剩余量rn不能再提取出更多的固有模态函数时停止。此时, 信号x(t)被分解成n个固有模态函数ci和一个剩余量rn:

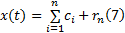
式中:剩余量rn代表了信号的平均趋势。

2 集总经验模态分解

针对EMD可能产生的模态混叠, 在EMD的基础上, 2009年黄锷又提出了改进后的算法, 也就是集总经验模态分解(EEMD)[7]。

EEMD是在EMD的基础上添加了高斯白噪声, 它把包含了信号和有界幅值的高斯白噪声的分量均值当做真实的IMF分量[8], 实质上是一种叠加了高斯白噪声的多次EMD处理。经过这一处理, 能够有效地消除模态混叠。EEMD的算法步骤如下[9]:

(1)初始化EMD执行的总次数M, 添加的白噪声的幅值系数为k, 令m=1。

(2)执行第m次EMD实验:在输入信号x(t)的基础上添加一随机高斯白噪声序列nm(t), 得到加噪的待处理信号y(t):

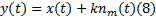
对信号y(t)进行EMD分解, 得到n个IMF分量, 用ci, m表示第m次实验得到的第i个IMF分量, i=1, 2, …, n。

如果m< M, 令m=m+1, 返回步骤(2)。

(3)对M次实验得到的每个IMF分量进行均值运算:

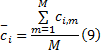
(4)输出 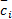作为EEMD的第i个IMF分量, i=1, 2, …, n。

添加的噪声对信号幅值的影响计算式为:

3 基于HHT和模糊C均值聚类的故障识别
3.1 特征提取

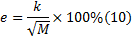
对式(7)中的每个固有模态函数ci(t)进行Hilbert变换得:

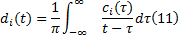
构造解析信号:

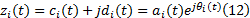
幅值函数:

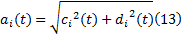
相位函数:

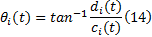
可以求出瞬时频率:

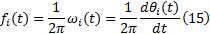
于是, 可以得出:

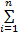
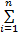
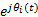
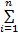
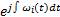
x(t)= ci(t)=Re ai(t) =

Re ai(t)

这里忽略了剩余量rn, Re表示取实部, 上式称为Hilbert谱, 记为:

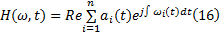
进一步定义Hilbert边际谱:

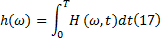
式中:T为信号的持续时间; H(ω , t)描述了信号的幅值随时间和频率的变化规律; h(ω )反映了信号的幅值随频率的变化情况。

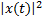
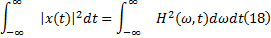
一般来说, 具有能量密度的含义, 那么H2(ω , t)也具有能量密度的意义。H2(ω , t)被称为Hilbert能量谱, 由能量守恒原理可以得到:

定义:

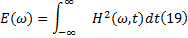
E(ω )被称为Hilbert边际能量谱。

信号经过EMD或者EEMD处理后, 得到一系列IMF分量, 选出涵盖信息最丰富的IMF分量后, 求出每个IMF分量的Hilbert谱, 记为Hi(ω , t), 则有:

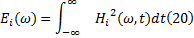
Ei(ω )被称为局部Hilbert边际能量谱。

由式(20)进一步定义基于局部Hilbert边际能量谱求出的特征能量:

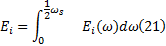
式中:i=1, 2, …, n; ω s为采样角频率。

以各IMF分量的特征能量占总特征能量的百分比构造特征向量, 即:

3.2 状态识别

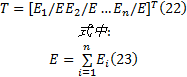
模式识别通常也被称为模式分类, 按照处理对象的性质和解决问题的方法, 又分为有监督的分类和无监督的分类。有监督的分类往往需要足够的先验知识, 无监督的分类又被称为聚类分析[10]。

聚类就是按照一定的要求或者规律对事物进行区分或者分类的过程, 在这一过程中, 没有关于分类的先验知识, 没有教师指导, 仅仅依靠事物之间相似性作为类属划分的准则。用模糊数学方法处理聚类问题称之为模糊聚类分析。模糊聚类分析目前应用最广泛的是基于目标函数的模糊聚类方法。其中又以模糊C均值聚类算法(Fuzzy C-means, FCM)理论最为完备。

FCM算法中, C是指将有限样本集{x1, x2, …, xn}划分为C类, 各个样本以一定的隶属度属于C个不同类。一般用μ ij表示第j(j=1, 2, …, n)个样本属于第i(i=1, 2, …, C)类的隶属度, μ ij应满足如下条件:

(1)μ ij∈ [0, 1], ∀ i, j。

(2) μ ij=1, 即任意一个样本对所有的聚类中心的隶属度之和为1。

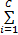
(3)0< 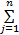μ ij< n, ∀ i, 每一类包含的样本个数在0和n之间。

模糊C均值聚类算法以类内加权平方误差和为目标函数:

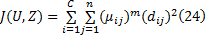
式中:U为初始隶属度矩阵; Z为聚类中心, Z=(z1, z2, …, zc); μ ij为隶属度矩阵元素; m为加权指数, m> 1; C为划分类别数; dij为样本点xj与第i类聚类中心zi的距离, 一般为欧氏距离, 计算公式为:

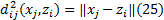
本文采用的是指定初始聚类中心的模糊C均值聚类算法, 先通过标准样本求出初始聚类中心, 然后将待检测样本组成的数据集使用FCM算法进行聚类分析, 从而进行模式识别。

3.3 本文算法的具体步骤

步骤1 对原始时域信号分别进行EMD处理和EEMD处理, 得到一系列固有模态分量, 结合短时最大熵谱和功率谱分析, 选出包含故障信息最丰富的一个IMF分量。

步骤2 对选出的IMF分量进行Hilbert包络解调, 对解调后得到的包络信号再次分别进行EMD处理和EEMD处理, 得到一系列IMF分量, 将前几个IMF分量相加进行重构, 计算重构信号与原信号的互相关系数以及占原信号的总能量比, 设定阈值, 选出构造特征向量的IMF分量。

步骤3 按照式(22)分别求出经过EMD和EEMD得到的特征向量。

步骤4 从数据集中选出一部分作为标准样本, 样本均值作为模糊C均值聚类算法的初始聚类中心, 余下的作为检测样本, 然后采用模糊C均值聚类算法进行模式识别。

4 诊断实例

诊断对象为某液压伺服系统中的斜盘式轴向柱塞泵, 型号为MCY14-1B, 柱塞数为7, 驱动电机额定转速为1470 r/min。试验时模拟正常、滑靴磨损、松靴、中心弹簧磨损、斜盘磨损5种状态, 采集泵壳振动加速度信号, 采样频率为50 kHz。在同一个系统压力20 MPa下每种状态采集3组数据, 每组数据采样时间为1.2 s。

在计算样本特征时, 每个样本截取其中时间长度为0.2 s的一段原始数据进行分析, 数据分析点数为10 000点。每种状态下从其中一组数据截取10段标准样本原始数据, 5种状态总共截取50段标准样本原始数据, 进行特征向量提取, 得到50个标准样本, 以这些标准样本的均值作为模糊C均值聚类的初始聚类中心。另外, 每种状态从另外两组数据中截取10段原始数据作为检测样本原始数据, 5种状态总共截取50段检测样本原始数据, 进行特征向量提取, 得到50个测试样本, 采用模糊C均值聚类算法进行模式识别。

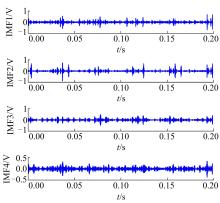
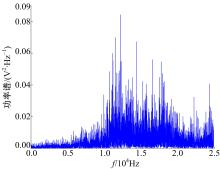
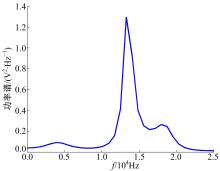
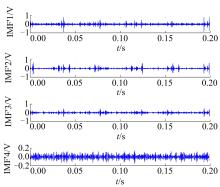
下面以滑靴磨损故障为例说明3.3节中步骤1~步骤3的样本特征向量提取过程。截取一段时间长度为0.2 s的滑靴磨损信号, 对时域信号进行EMD处理, 得到的前四阶IMF分量如图1所示。对IMF 1做功率谱分析, 如图2所示。对滑靴磨损信号做短时最大熵谱分析, 结果如图3所示。

图1 EMD处理后的前四阶IMFFig.1 Preceding four order IMFs after EMD processing

由图2和图3可以发现, IMF1共振明显, 所处的频率段与短时最大熵谱分析结果吻合, 因此选择IMF1进行分析。

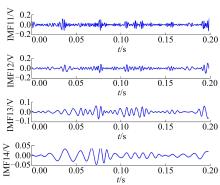
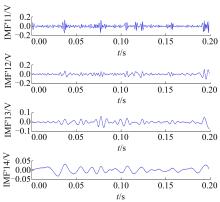
图2 IMF1功率谱Fig.2 Power spectrum of IMF1

图3 短时最大熵谱分析Fig.3 Short-term maximum entropy spectrum analysis

对IMF1进行Hilbert包络解调, 然后降低采样频率至2 kHz, 对降低采样频率后的包络信号再次进行EMD分解, 得到一系列IMF分量, 选取的前四阶分量为IMF11~IMF14, 结果如图4所示。

图4 二次EMD处理后的IMF11~IMF14Fig.4 IMF11~IMF14 after second EMD processing

选取前4个IMF分量相加进行重构, 计算得出重构信号与原信号的互相关系数为0.9675, 重构信号能量占原信号总能量百分比为94.76%, 说明前四阶IMF分量的重构信号含有原信号绝大部分信息, 因此选择前四阶分量构造特征向量。

采取与前述EMD相同的处理过程对滑靴磨损信号进行EEMD处理, 得到的前四阶IMF如图5所示。

图5 EEMD处理后的前四阶IMFFig.5 Preceding four order IMFs after EEMD processing

对IMF1再次进行EEMD处理, 选取的前四阶IMF分量为IMF11~IMF14, 结果如图6所示。

图6 二次EEMD处理后IMF11~IMF14Fig.6 IMF11~IMF14 after second EEMD processing

同理, 计算得出重构信号与原信号互相关系数为0.9742, 重构信号能量占原信号能量百分比为97.44%, 因此也选择前四阶分量构造特征向量。

在计算特征向量的过程中, 先求出每种状态各10个标准样本的4维特征向量, 5种状态共得到50个标准样本的4维特征向量, 以标准样本均值作为模糊C均值聚类算法的初始聚类中心; 再求出每种状态各10个测试样本的4维特征向量, 5种状态共得到50个检测样本的4维特征向量。表1、表2分别为经过EMD、EEMD处理得到的样本初始聚类中心和部分检测样本。

表1 EMD处理得到的初始聚类中心及部分检测样本 Table 1 Initial clustering center and partial test samples obtained by EMD processing

表3、表4分别为经过EMD、EEMD算法得到的对50个检测样本的分类识别结果。表1~表4中Ⅰ 、Ⅱ 、Ⅲ 、Ⅳ 、Ⅴ 分别代表正常、滑靴磨损、松靴、中心弹簧失效以及斜盘磨损5种状态。

表2 EEMD处理得到的初始聚类中心及部分检测样本 Table 2 Initial clustering center and partial test samples obtained by EEMD processing

表3、表4中数字代表检测样本的编号, 1~10代表正常状态, 11~20代表滑靴磨损, 21~30代表松靴, 31~40代表中心弹簧失效, 41~50代表斜盘磨损。黑体数字代表识别正确的样本编号。模糊C均值聚类算法对检测样本进行分类过程中的迭代次数如下:EMD算法为45次, EEMD算法为20次。

表3 EMD处理后模糊C均值聚类结果 Table 3 Fuzzy C-means clustering results after EMD processing

从表1和表2可以看出:经过EEMD处理得到的样本同类之间波动性比EMD处理得到的样本要小, 同类样本之间聚类效果好, 异类样本之间区分度大。

表4 EEMD处理后模糊C均值聚类结果 Table 4 Fuzzy C-means clustering results after EEMD processing

从表3可以看出:50个样本中能够准确识别出来的样本只有24个(黑体数字), 尤其是中心弹簧失效全部误分, 总体识别准确率只有48%。

而从表4可以看出:50个样本中, 仅有3个(11, 16, 17)滑靴磨损样本误分为斜盘磨损样本, 识别准确率提高到94%。

5 结论

(1)通过短时最大熵谱以及功率谱分析, 准确地找出了包含故障信息最敏感的IMF分量。再对该分量进一步使用EMD和EEMD进行处理, 对二次分解得到的IMF分量进行重构, 通过计算重构信号与原信号的互相关系数和占原信号能量百分比, 能够从分解出来的IMF分量中选取对故障敏感的IMF。

(2)模糊C均值聚类算法识别结果表明:本文提出的特征向量能够准确地反映轴向柱塞泵的故障特征, 证明了特征向量的提取方法的有效性。

(3)识别结果对比表明:利用EEMD方法处理数据的故障确诊率高于用EMD方法处理数据的故障确诊率。

(4)EEMD处理得到的特征向量比EMD处理的波动性小, 同类样本之间聚类效果好, 异类样本之间区分度大。在采用模糊C均值聚类算法对样本进行聚类过程时, 利用经EEMD处理所得数据进行聚类需要的迭代次数明显少于利用经EMD处理所得数据进行聚类的迭代次数。

The authors have declared that no competing interests exist.

参考文献
[1] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proc R Soc Lond A, 1998, 454(1971): 903-995. [本文引用:1]
[2] 卢传奇. 基于HHT和模糊C均值聚类的液压泵故障诊断研究[D]. 秦皇岛: 燕山大学机械工程学院, 2012.
Lu Chuan-qi. Research on HHT and fuzzy c-means clustering based hydraulic pump fault diagnosis[D]. Qinhuangdao: College of Mechanical Engineering, Yanshan University, 2012. [本文引用:1] [CJCR: 0.3302]
[3] 张邦礼, 尹朝东, 曹龙汉. 柴油机故障诊断中的遗传与模糊C均值混合聚类分析算法[J]. 计算机工程与应用, 2002(3): 254-256.
Zhang Bang-li, Yin Chao-dong, Cao Long-han. Clustering by hybrid genetic/C-means algorithm in fault diagnosis for diesel engines[J]. Computer Engineering and Applications, 2002(3): 254-256. [本文引用:1]
[4] 诸葛起, 路甬祥. 用振动信号检测柱塞泵松靴故障[J]. 振动、测试与诊断, 1989, 9(3): 11-15.
Zhuge Qi, Lu Yong-xiang. Plunger pump loose boots fault detection based on vibration signal[J]. Journal of Vibration, Measurement & Diagnosis, 1989, 9(3): 11-15. [本文引用:1]
[5] 雷亚国. 基于改进Hilbert-Huang变换的机械故障诊断[J]. 机械工程学报, 2011, 47(5): 71-77.
Lei Ya-guo. Machinery fault diagnosis based on improved Hilbert-Huang transform[J]. Journal of Mechanical Engineering, 2011, 47(5): 71-77. [本文引用:1] [CJCR: 0.544]
[6] 雷达, 钟诗胜. 基于奇异值分解和经验模态分解的航空发动机健康信号降噪[J]. 吉林大学学报: 工学版, 2013, 43(3): 764-770.
Lei Da, Zhong Shi-sheng. Aircraft engine health signal denoising based on singular value decomposition and empirical mode decomposition methods[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(3): 764-770. [本文引用:1] [CJCR: 0.701]
[7] Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. [本文引用:1]
[8] 张玲玲, 骆诗定, 肖云魁, 等. 集合经验模式分解在柴油机机械故障诊断中的应用[J]. 科学技术与工程, 2010, 10(27): 6745-6749.
Zhang Ling-ling, Luo Shi-ding, Xiao Yun-kui, et al. Application of EEMD in fault diagnosis of diesel engine[J]. Science Technology and Engineering, 2010, 10(27): 6745-6749. [本文引用:1] [CJCR: 0.2471]
[9] Lei Y G, He Z J, Zi Y Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery[J]. Mechanical Systems and Signal Processing, 2009, 23(4): 1327-1338. [本文引用:1] [JCR: 1.913]
[10] 王连锋, 宋建社, 朱昱, 等. 基于模糊聚类分析的证据组合[J]. 系统工程与电子技术, 2013, 35(1): 113-119.
Wang Lian-feng, Song Jian-she, Zhu Yu, et al. Systems evidence combination based on fuzzy clustering analysis[J]. Engineering and Electronics, 2013, 35(1): 113-119. [本文引用:1]