顾天奇(1983-),男,博士研究生.研究方向:智能精密制造.E-mail:gutianqi2011@126.com
基于移动最小二乘法构造了一种新的封闭离散点拟合方法。该方法利用移动最小二乘法基于点的拟合原理,在离散点之间定义拟合点,划分支持域半径,实现了支持域有序的划分方式。基于封闭离散点的几何特征,提出一种新的权值确定方法,该方法通过构造一个与弦长有关的点,赋予支持域内各点的权值,使临近点的权值变化逐步衰减,实现了拟合曲线的局部逼近。利用提出的封闭曲线拟合方法对叶片截面形线离散点进行拟合,验证了该方法的有效性。
A new curve fitting method based on moving least square is constructed for closed discrete points. According to the moving least square theory, the fitting point is obtained between discrete points and the influence domain with defined radius is determined in order. Considering the geometric features of discrete points, a new approach to determine the weights of neighbor points is proposed for the local approximants by constructing a point associated with the chord length, which makes the weights of neighboring points vary decreasingly. The discrete points of blade-section profile are fitted and the results confirm and validate the proposed fitting method.
一直以来, 曲线重构的方法都是几何造型中重要的研究课题之一。20世纪80年代, Fritsch等[1, 2]针对有序离散点提出了用分段三次曲线进行曲线插值的方法; Passow等[3]研究了用样条函数进行曲线重建的方法, 后来Lavery等[4]提出一种多尺度样条拟合数据点的方法。最小二乘法拟合是最早用于曲线曲面重构的方法。然而, 对具有复杂几何特征的离散点进行拟合不具备局部逼近的性质, 重建的曲线并不能够反映出原始离散点的形状。1981年, Lancaster等[5]提出一种新的曲面拟合方法— — 移动最小二乘法(Moving least square, MLS), 该方法可看作是标准最小二乘法的推广形式。与传统的最小二乘法相比, 移动最小二乘法建立拟合函数不是采用传统最小二乘法的完备多项式, 而是由一个与自变量有关的系数向量和完备多项式基函数构成, 且利用具有紧支性的权函数在划分支持域的同时, 也对离散点赋予了一个权值, 使拟合曲线具有局部逼近的性质。后来, 移动最小二乘法成为无网格方法构造形函数的重要方法之一, 在无网格方法中得到了广泛的应用。近年来, 国内外学者对移动最小二乘法做了大量的研究。Mukherjee等[6]改进了移动最小二乘法, 便于无单元Galerkin方法处理边界条件; 陈美娟等[7]以带权的正交函数作为基函数, 避免了病态方程组的求解问题; 程玉民等[8, 9, 10, 11]提出了复变量移动最小二乘法及其相应的弹性力学复变量无网格方法。但是, 针对叶片等封闭曲线曲面, 移动最小二乘法传统的支持域划分方式和权值确定方式难以实现重构。本文提出一种新的支持域划分方式与权的赋值方式, 以叶片截面形线离散点为算例, 实现了封闭离散点的曲线拟合, 证明了该方法的有效性。
将拟合函数表示为如下形式:

式中: 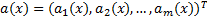
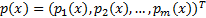
线性基: 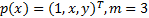
二次基: 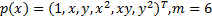
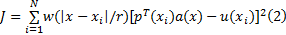
式中: N为支持域内的离散点数; r为划分的支持域半径; w(s)(s=|x-xi |/r)为权函数, 一般w(s)应有以下的特点:
(1)当 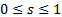
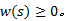
(2)在[0, 1]中单调递减且连续可导。
(3)当 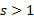
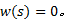
式(2)写成矩阵形式为:
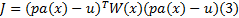
式中: 
基于最小二乘原理求得:
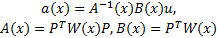
代入式(1)得出函数 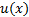
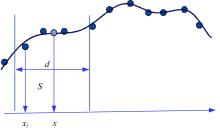
移动最小二乘法通过构造具有紧支性的权函数将拟合区间进行局部区间划分及权的赋值, 在支持域内利用最小二乘法确定局部拟合的系数, 从而实现全局拟合, 其原理如图1所示。其中, S为拟合点与离散点的投影距离; d为支持域半径。
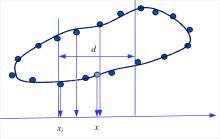
移动最小二乘法支持域传统的划分方式是基于向 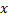
针对封闭离散点的这一特点, 本文在相邻的离散点之间确定 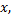
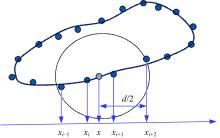
从图3可以看出:通过这种方式, 可以确定性地选择支持域内的点数, 而支持域的半径可由支持域内与 
移动最小二乘法利用具有紧支性的权函数对支持域内的点分配权值, 权的大小与 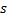
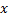
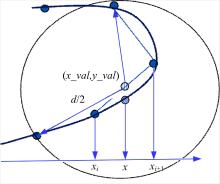
从图4可以看出:基于 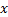
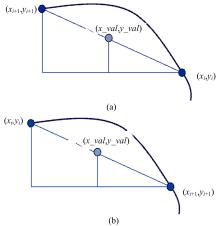
在两临近离散点xi 与xi+1 之间定义x, 取通过两点直线上的一点(x_val, y_val), 令x_val=x, 支持域内各点的权值w(s(xi))由该点到各点的距离决定, 且:
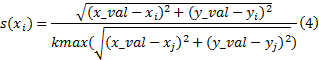
式中: 
支持域半径的选择与支持域内离散点到点(x_val, y_val)的距离有关, 合理地选取k值能够保证支持域内各点的权值w(s(xi))在权函数的衰减区, 控制曲线局部逼近的程度。从图5可以看出, 此种权的赋值方式与拐角处离散点的几何特征有关, x支持域内沿着离散点两个方向的临近点权值呈现逐步衰减的趋势, 保证了拐角处拟合曲线的逼近性质。在这里, 需要确定 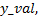
针对图6的两种情况, 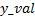
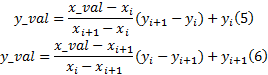
本文以叶片截面形线的离散点为例进行曲线拟合, 算法程序利用MATLAB软件实现。该数值算例的参数为:
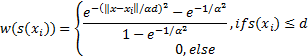
式中: 
(2)线性基函数: 
(3)支持域内点数:N=4。
(4)系数:k=10。
(5)离散点数:n=199。
该算法程序的流程如下:
(1)读取叶片截面形线的离散点。
(2)在离散点间定义 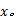
(3)对每一个 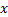
a.确定 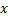
b.确定 
c.计算 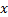
d.计算 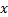
(4)结束循环, 连接节点值, 形成拟合曲线。
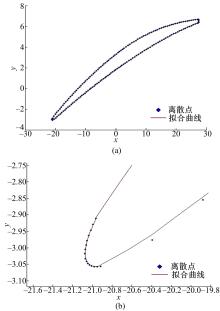
根据本文提出的支持域划分方式以及权值确定方式对叶片一条截面形线的离散点进行拟合, 结果如图8所示。对叶片较薄部分的截面形线离散点进行拟合, 结果如图9所示。叶片在靠近边缘处较薄,
截面形线拐角处离散点的几何特征呈现急剧的变化, 这要求拟合方法具有很好的逼近性。
该方法通过设置不同的参数(如基函数、权函数、支持域内点数等), 可以调整曲线的平滑性以及曲线逼近的程度。与样条函数相比, 该方法采用低阶基函数就可以实现良好的逼近效果, 且操作简便灵活、易于实现。
用移动最小二乘法进行曲线拟合时, 不需要事先确定拟合函数的类型, 由于紧支权函数的引入, 在不需要分段拟合的情况下具备局部逼近的性质, 能够很好地反映离散点的几何特征。本文提出一种基于移动最小二乘原理的封闭离散点拟合方法。该方法在相邻离散点之间定义 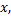
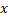
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|