王晓燕(1975-),女,博士研究生.研究方向:数控机床可靠性.E-mail:wlfn2005@163.com
基于大量故障数据分析,对故障链类型进行分类。利用子系统相关故障率、相关系数和独立故障率之间的关系,建立了复杂系统故障相关系数模型,并以实例验证。本文解决了多系统复杂相关关系的相关系数计算问题,完善了相关系数理论体系,对精确可靠性设计、优化维修计划具有重要意义。
The degree of interaction between dependent systems determines the error between the theory reliability and field reliability. So the dependent coefficient between the dependent systems is an important reference for design reliability and distribution reliability. However, the existing method can only estimate the dependent coefficient of a simple chain which includes two systems. In this work, the interaction in failure chains is classified after investigating large amount of failure data. Based on the types of failure chains, a model of dependent coefficient for complex system is developed using the function relationships among the dependent failure rate, independent failure rate and dependent coefficient of subsystems. A case study is carried out to verify the developed model. Results show that the model can estimate the dependent coefficient of a complex system, and improve the theory. It is very important to more precisely design the reliability growth and to optimize the repair and maintenance schedules.
机械装备相关故障的存在造成了其固有故障率的变化, 可靠性设计与分配阶段若忽视了子系统之间的故障相关性, 则可靠性的设计值必然与生产实际发生值存在误差。系统故障中有3种最典型的相关故障:串联故障、负相关故障和共因失效[1, 2]。本文讨论的是这3种相关故障以外的另一种相关故障形式— — 相互作用故障(Interactive failures, 简称I.F), 如某个部件A在发生故障时会加速或导致部件B的故障的发生, 有时这种破坏作用是相互的。这种相互作用的结果导致了故障系统的故障率上升, 上升的幅度与子系统之间相互影响的程度有关。子系统之间相关的程度称之为相关系数[3, 4]。关于相关系数研究的文献较少, 仅有的文献也因为研究模型的不同, 估算方法迥异。各个计算方法和模型均在一定程度上实现了相关系数的求解, 但都存在着一定的理论局限。主要的估算手段有:①数理统计法[5], 利用相关故障发生率作为相关系数, 样本采集数量的多少决定了相关系数的变化, 误差较大。②试验法[3], 利用试验手段验证模型并计算相关系数。该方法针对性较强, 且实现成本较高, 不具有普遍推广性。③主观赋值法[6, 7], 有经验的专家对相关系统之间的相关程度打分, 计算综合评分值作为相关系数。该方法主观性较强, 且赋值误差较大。④Copula函数法[8, 9, 10], Copula函数描述的是变量之间的相关性, 将变量联合累积分布函数同变量边缘累积分布函数连接起来的函数, 可利用子系统的相关故障数据计算出子系统之间的相关系数, 这个相关系数是共同且唯一的。该方法计算较为复杂, 且不能明确子系统之间的相互作用关系和作用方向, 因此模型无法实现多系统之间错综复杂的多个相关系数的计算。⑤窄界理论法[11, 12, 13], 利用相关子系统的主要故障模式的功能函数计算相关系数, 该方法只适合于零部件本身的多模相关, 由于无法确定多系统之间主要故障模式的功能函数的相关关系, 因此很难实现多系统之间的相关系数的计算。⑥故障率法[4], 利用相关子系统之间故障率的关系式推导出相关系数。文献[4]仅仅给出了简单的两个相关子系统之间的相关系数的计算, 多系统之间的复杂相关关系没有进一步推导。这6种研究方法中, 方法④和方法⑥更适合于多系统中相关关系的研究, 但是两种模型对相关系数的计算均局限于两两相关系统。本文针对以上方法的局限, 对多系统相关形式进行了大量的故障数据分析研究, 对相关故障链进行了种类划分, 针对不同的故障链形式利用相关故障率与独立故障率和相关系数之间的关系, 在掌握I.F故障数据变化的特征的条件下, 提出假设条件, 建立了基于故障链的复杂系统故障相关系数的求解模型。
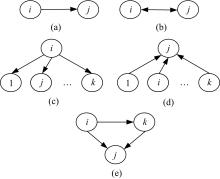
由机械装备的故障数据统计分析可知, 对故障子系统来说, I.F的相关关系分为影响与被影响两种形式, 根据包含的相关子系统数量和作用形式主要存在如下5种相关故障链, 如图1所示。
图1中, (a)为单向相关, 是I.F类型中的基本单元, 只存在子系统 

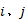

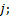

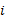
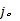
对大量故障数据统计分析发现, 具有相关故障的子系统 
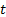
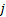
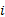
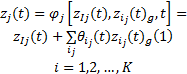
式中: 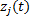
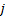



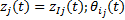
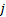


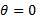
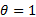
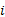
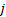
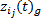
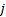
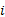
公式(1)为子系统 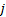


基于故障链的相关系数的求解分为以下3种情况讨论:
(1)相关类型为简单单向, 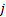
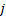
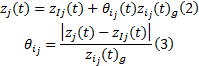
由于相关子系统 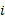
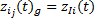
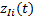
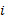
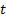
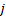
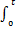
(2)相关类型为多系统单向相关, 如图1(d)所示, 故障终点 
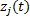

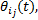
假设① 子系统 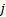
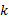
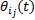
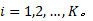

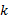

式中: 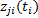
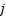
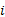


假设② 子系统 
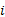
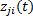
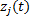
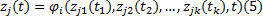
以图1(d)的关系形式为例, 子系统 
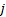


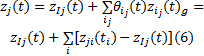
(3)相关类型为多系统复杂相关, 如图1(b)(e)所示, (b)可视为(e)的特例, 

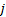

由式(4)可推导出:
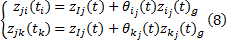
式中: 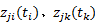
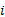

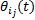
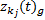




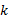
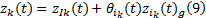
由于 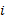
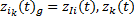
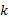
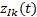


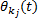
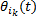
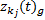
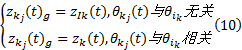
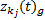
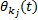
至此, 对于复杂系统的I.F类型的相关关系的相关系数计算模型体系得以建立。
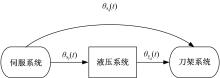
本文以某型号数控机床3个子系统之间的复杂相关关系为例。数据来源于某同一型号175台机床13个月的生产故障跟踪记录。图2为该型号数控机床的3个子系统之间的某相关关系图, 箭头的指向为被影响系统, 三者之间相关故障类型为复杂的相关故障链类型。伺服系统为相关故障起点, 不受其他系统作用。其中, 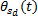
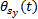
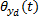
表1为该型号机床3个子系统生产现场故障间隔时间的跟踪记录值, 包含了3个子系统相关故障数据。
| 表1 子系统故障间隔时间 Table 1 Time between failures of subsystems |
设 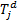

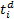
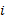


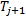
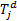

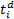
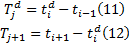
机床的各个子系统排除相关故障, 在正常标准的生产状态下其故障率为其本身固有的独立故障率, 可靠性函数符合威布尔分布。
伺服系统为:
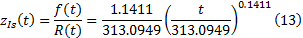
液压系统为:
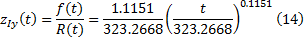
刀架系统为:

对图2中的3个子系统的相关关系分析以求得刀架系统的综合故障率为例, 根据式(1), 刀架系统的综合故障率 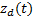

式中: 
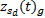

3个子系统的综合故障率由生产现场收集到的故障数据建模得到。
伺服系统为:
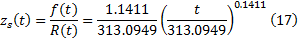
液压系统为:
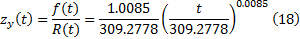
刀架系统为:
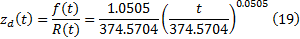
根据式(4), 将式(16)分解成刀架系统分别与伺服系统和液压系统的分故障率模型如下:
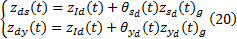
式中: 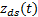
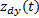
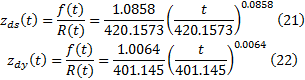
由式(20)可得:
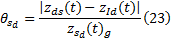
由于伺服系统为故障起点, 所以有:
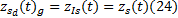
将故障率模型(13)(15)(21)代入方程(23), 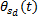
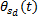
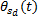
由式(20)可得:
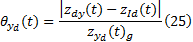
式中: 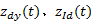
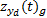
液压系统对刀架系统的相关故障与伺服系统-液压系统的故障链相关, 即伺服系统对液压系统的相关系数 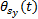


将故障率模型(15)(18)(22)代入式(25), 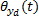
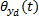
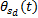
至此, 对于任何错综复杂的相关关系, 只要满足对同一子系统的所有直接相关关系的相关系数线性无关的条件, 由以上创建的求解模型就可以计算出复杂系统中相关故障的相关系数。
(1)以相互作用的相关故障为研究对象, 总结出其在数控机床故障中存在的五种故障链类型, 基于此建立了此种相关故障类型的相关系数计算模型体系。
(2)复杂相关故障链中相关系数的计算模型的成立建立在两种假设基础之上, 即对同一子系统的所有相关故障关系之间互相独立, 并且综合故障率与分故障率成函数关系。
(3)本文研究成果拓展了故障相关性研究领域, 创建了相关系数计算模型体系, 使精确预测、设计多系统之间相关运动的可靠度成为可能, 并为后续制定、优化机械设备维修保养提供了理论依据。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|