立铣加工系统包括刀具、刀柄、主轴、主轴箱以及其他结构, 其动力学特性主要指刀柄安装刀具后刀尖点位移导纳。由于主轴、主轴箱等结构复杂, 存在结合部等原因, 一般难以精确建立其解析或有限元模型, 因此采用解析方法或有限元软件进行刀尖点位移导纳预测的结果一般准确性较差^{[1, 2]}。近几年, 学者们采用导纳综合子结构法(RCSA)^{[3, 4, 5]}研究立铣加工系统的建模及动态特性预测。将刀柄和主轴、主轴箱以及其他结构作为一个子结构, 通过试验方法测试获得其位移导纳。刀具子系统因为结构简单可采用有限元方法分析获得其位移导纳, 然后将试验获得的刀柄子结构位移导纳和有限元方法获得的刀具子结构位移导纳进行耦合, 求解立铣加工系统的刀具刀尖点位移导纳。

立铣加工系统中包含主轴、刀柄的部分一般不经常变化, 而安装进刀柄的刀具则根据加工需要发生变化。Schmitz等^[3]首先采用导纳综合子结构方法将刀具和刀柄等进行结合。刀柄、刀具的模型采用单点结合, 结合节点具有横向位移和弯曲自由度。单点结合模型虽然结合点少, 但是每个节点有2个自由度, 需要研究弯矩和横向力的双重作用。目前已证明了在单点结合模型中忽略节点的转角自由度, 而仅考虑节点横向位移的子结构方法不能准确预测结构的耦合导纳^{[6, 7, 8, 9]}。但是, 刀柄子结构的转角的测量和弯矩的施加在工程上实现目前仍存在困难, 因此通过试验测试获得刀柄子结构位移导纳难以实现。针对上述问题, Park等^[10]提出一种通过2次锤击法测试间接求解刀柄子结构与转角和弯矩相关的位移导纳函数的方法。但是这种方法求解过于复杂, 测试中的噪声等引起的误差将导致求解失效。Movahhedy^[11]提出两点结合模型, 采用有限元方法证明两点结合模型与到点结合模型在求解结构固有频率和阵型的问题具有相同的效果。两点结合模型在每个结合点只考虑横向位移自由度, 避免了转角和弯矩引起的分析和测量问题, 模型具有一定的先进性。

本文将刀柄与主轴及其他部件看做一个子结构, 称作刀柄子结构, 把刀具本身当做刀具子结构。在Movahhedy提出的模型基础上, 采用导纳综合法求解了刀柄、刀具两点结合后刀尖点位移导纳的理论表达式。最后, 进行了算例研究, 与有限元仿真结果进行对比验证了两点结合导纳综合法的预测准确性。

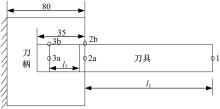
刀柄子结构与刀具子结构两点结合模型如图1所示。刀柄与主轴相连, 将主轴箱、主轴和刀柄看做一体。刀柄和刀具子结构在两个单点相互结合。铣床的主轴一般径向刚度远小于轴向刚度, 加工过程中振动形式主要为主轴、刀柄和刀具组成系统的横向弯曲振动。因此可将主轴、刀柄和刀具等看作梁结构。刀柄子结构上的结合点定义为2b和3b, 刀具子结构上的结合点定义为2a和3a。刀柄上2b和3b之间的距离与刀具上2a和3a之间的距离相等。刀具刀尖点定义为1点。刀柄和刀具的结合部以两对结合点之间的两对弹簧-阻尼单元相连接。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 刀柄、刀具子结构两点结合模型Fig.1 Two points coupling model of holder and tool

如图2所示建立坐标系, 定义刀柄和刀具子结构上的位移导纳为

式中: x_i 为i点的横向位移; f_j 为作用在j点的横向力。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 刀柄、刀具两点无阻尼柔性结合Fig.2 Simplified model of holder-tool

定义刀柄和刀具结合后刀具刀尖点原点位移导纳为 H₁₁, H₁₁=X₁/F₁。其中, X₁为整体结构刀具刀尖点的横向位移, F₁为整体结构刀具刀尖点的横向力。

首先考虑刀柄与刀具无阻尼两点柔性结合情况, 由力平衡条件得:

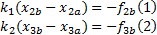
由兼容条件得:

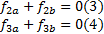
另外, 有:

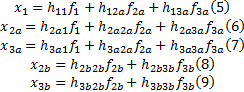
将式(6)(8)和式(7)(9)分别代入式(1)得:

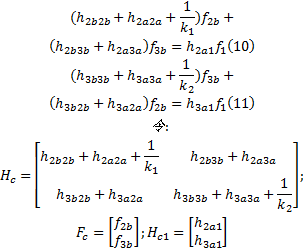
则式(10)(11)可改写为:

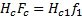
令 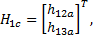式(5)可写为:

若考虑黏性阻尼柔性结合, 则图2中点2a、2b和点3a、3b之间分别由一个线性弹簧和黏性阻尼单元组成。线性弹簧的刚度分别为 则点2a、2b和点3a、3b之间刚度 定义为:

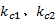
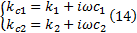
式中: i为虚数单位; ω 为频率。

将式(14)代入式(13)中可得包含阻尼项的刀尖点位移导纳函数的表达式。弹簧刚度 k₁ 、k₂, 黏性阻尼系数c₁ 、c₂值与刀柄刀具连接方式有关系。文献[7]研究了采用系统辨识技术获得结合部参数的方法。

采用遗传算法进行参数辨识, 变量个数共4个, k₁, c₁, k₂, c₂ 。由式(6)可知, 为了辨识参数, 必须事先获得R₁₁, R_12a, R_2a1, R_2a2a, R_2b2b 以及H₁₁ 。

进行模型辨识之前, 采用梁理论或有限元方法获得 R₁₁, R_12a, R_2a1, R_2a2a位移导纳。铣刀柄位移导纳函数R_2b2b 和H₁₁通过试验方法获得。各位移导纳是关于频率的函数, 测试和理论分析获得的导纳函数必须具有相同的维数, 并且频率的间距相同。

优化目标函数的输入是位移导纳数组 R₁₁, R_12a, R_2a1, R_2a2a, R_2b2b 和H₁₁ 以及频率向量w。输出为优化目标。

由式(6)得优化目标为 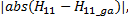其中 表示取向量的模。编码方式采用实数编码, 种群个数可取为20。

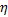
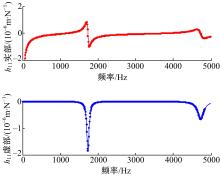
为验证方法的正确性, 采用可精确建模的刀柄和刀具进行建模和分析。刀柄为直径24 mm的圆柱, 长80 mm, 刀具安装孔直径为12 mm, 深为35 mm。刀柄弹性模量为200 GPa, 密度为7800 kg/m³, 泊松比为0.3, 阻尼因子 为0.02。刀具直径为d=12 mm, 弹性模量为200 GPa, 密度为7800 kg/m³, 泊松比为0.3, 阻尼因子η =0.02, 长度为175 mm, 插入刀柄内部部分长度l₂=28 mm, 剩余部分长度为l₁=147 mm, 如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 刀具结合处尺寸Fig.3 Dimension of the tool and holder

基于有限元分析软件Ansys按照图2所示建立刀柄模型。刀柄长为80 mm, 刀具安装孔与刀柄直径相同, 均为12 mm。刀柄有限元模型采用beam188梁单元, 分两段建立模型。有限元模型总共包含15个单元, 在其最左端(非刀具安装端)约束位移和转角自由度。分别在2b点和3b点进行激励, 在0~5000 Hz进行谐响应分析, 获得位移导纳h_2b2b, h_3b2b, h_2b3b, h_3b3b, 其中h_3b2b如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 位移导纳h3b2bFig.4 Displacement receptance h3b2b

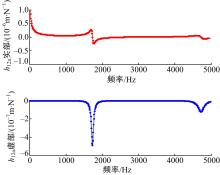
同样, 基于Ansys软件使用Beam188单元建立刀具的有限元模型, 刀具模型共计25个单元。建立模型时保证在刀具子结构上的两个节点2a和3a分别与刀柄子结构上的节点2b和3b具有相同的轴向坐标。分别在刀具子结构1、2a、3a点施加力, 在0~5000 Hz范围内进行谐响应分析。获得位移导纳h₁₁, h_2a1, h_3a1, h_12a, h_2a2a, h_3a2a, h_13a, h_2a3a, h_3a3a, 其中h₁₁和h_12a如图5、图6所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 位移导纳h11Fig.5 Displacement receptance h11

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 位移导纳h12aFig.6 Displacement receptance h12a

刀具与刀柄连接简化为2个弹簧阻尼单元, 利用遗传算法工具箱Gatool, 设定优化参数个数为4, k₁、k₂初值范围为[10⁷ 10¹⁴], c₁和c₂值的范围为[0 100], 经过50次优化后获得的参数如下:k₁=k₂=1× 10¹² N/m; c₁=c₂=0.35 Ns/m。

由有限元方法获得刀具子结构和刀柄子结构的各位移导纳, 利用Matlab软件编写程序, 按照式(13)计算刀具子结构和刀柄子结构结合后整体结构刀尖点位移导纳h₁₁。其中刀具刀柄结合部按式(14)计算其复刚度。

为验证文中方法预测结果的准确性, 使用Ansys软件按图3中几何尺寸建立刀具刀柄整体有限元模型, 刀具与刀柄子结构的结合采用两个Combine14单元, 单元属性如下:k₁=k₂=1× 10¹² N/m; c₁=c₂=0.35 Ns/m。由本文方法计算得到的刀具安装后刀尖点位移导纳如图6所示。

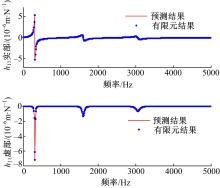
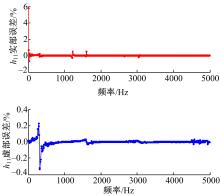
由图7可知, 采用两点结合导纳综合方法获得的整体刀尖点位移导纳与有限元方法建立的刀柄刀具整体模型分析获得的位移导纳几乎一致, 能够准确获得前三阶固有频率。为了分析两种方法获得的位移导纳的差别, 计算两种方法的相对误差, 如图8所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 预测结果对比Fig.7 Comparison of the FEA and analytical method

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 理论预测误差Fig.8 Error of the analytical prediction

由图可知, 两者相对实部误差最大为6%, 此时频率接近零赫兹, 当频率稍大于1 Hz时, 实部相对误差为0.7%。虚部相对误差最大为0.33%。

如图9所示, 采用丹麦B& K公司的3560B硬件采集系统及Pulse振动信号测试分析软件, 美国PCB公司三轴加速度传感器PCB356A24, 模态力锤PCB086C01, Z7030铣床等组成试验装置。铣床刀柄型号为莫氏3号弹簧夹套。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 试验装置Fig.9 Test equipment

45号钢待测件直径为12 mm, 长度为147 mm, 材料密度为7.8× 10³ kg/m³, 弹性模量为200 GPa, 泊松比为0.3, 阻尼比为0.02, 插入刀柄部分长度均为24 mm。

采取试验的方法获得刀柄的位移导纳h_2b2b, h_3b2b, h_2b3b, h_3b3b, 然后利用分量分析法识别刀柄的模态质量、模态刚度、模态阻尼。然后再利用这3个参数拟合出h_2b2b, h_3b2b, h_2b3b, h_3b3b的理想位移导纳曲线。其中h_2b2b的试验结果和拟合结果如图10所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 h2b2b的拟合结果Fig.10 Fitting results of h2b2b

由于刀具在试验过程中使用的是理想模型, 所以仍然采用有限元的方法获得刀具子结构的位移导纳h₁₁, h_2a1, h_3a1, h_12a, h_2a2a, h_3a2a, h_13a, h_2a3a, h_3a3a。

由有限元方法获得的刀具子结构和分量分析法拟合刀柄子结构的各位移导纳, 利用Matlab软件编写程序, 按照式(13)计算刀具子结构和刀柄子结构结合后整体结构刀尖点位移导纳h₁₁。其中刀具刀柄结合部按式(14)计算其复刚度, k₁=k₂=1× 10¹² N/m, c₁=c₂=0.35 Ns/m。

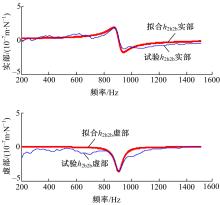
采取试验的方法获得刀具与刀柄结合后整体结构刀尖点位移导纳h_11new, 与两点结合导纳综合法获得的刀尖点位移导纳h₁₁进行比较, 比较结果如图11所示。由图可知, 文中所提方法与试验结果有很好的一致性。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 试验与理论结果对比Fig.11 Comparison of experimental and theoretical results

针对立铣加工系统刀具子结构和刀柄子结构结合部提出一种两点结合动力学模型。采用导纳综合法研究了两点结合模型的刀尖点位移导纳计算公式。利用Ansys软件进行刀具子结构和刀柄子结构位移导纳分析, 导出位移导纳数据。通过Matlab软件编写两点结合导纳综合法程序, 获得了刀尖点位移导纳函数。

用Ansys软件建立了刀具子结构和刀柄子结构整体有限元模型, 分析获得了刀尖点位移导纳函数。与两点结合导纳综合法分析结果进行比较并计算了两者相对误差, 结果表明, 在关注频率范围内相对误差最大为0.7%。在Z7030铣床上进行了试验研究, 用锤击法测试获得的刀尖点位移导纳和两点结合模型的导纳综合法获得的位移导纳有很好的一致性。