宋宝玉(1958-),男,教授,博士生导师.研究方向:摩擦学,机械故障诊断.E-mail:sby@hit.edu.cn
为了准确识别转速波动的斜齿轮早期故障特征,提出了基于光电编码器等角度采样的角度域同步平均降噪与阶次分析相结合的故障诊断方法。首先基于时域同步平均原理提出了角度域同步平均算法,采用光电编码器作为外触发器对时域信号进行等角度采样,然后将重采样信号在角度域内进行同步平均,消除与给定频率无关的周期信号和随机噪声的干扰,再利用阶次分析提取故障特征,最后通过斜齿轮点蚀故障诊断试验验证了该方法的有效性。
In order to accurately identify the early fault feature of helical gear, a new diagnosis algorithm is proposed based on the angular domain synchronous average and order tracking analysis. First, employing the concept of time domain synchronous average, an algorithm of angular domain synchronous average is put forward to reduce the noise interference. Using optical encoder as the external trigger, the vibration signals is angular domain are obtained by resampling the vibration signals of time domain according to the encoder pulse. By angular domain synchronous average processing, the irrelevant periodic signals and noise interference are reduced. Then, the fault features of helical gear rotating at low speed are extracted by the order tracking analysis. Experiment results of pitting fault diagnosis verify the effectiveness of the proposed algorithm.
斜齿轮具有传动平稳、低噪声和承载能力大等优点, 被广泛地应用于机械传动装备中。但是低速工况下的斜齿轮早期故障诊断较为困难。当斜齿轮在低速条件下运转时, 轮齿表面的局部故障产生的振动冲击能量较小, 由于受到轴和轴承等旋转部件的振动干扰, 其故障特征很难被提取到。另外, 齿轮早期故障通常发生在单个齿面或者很少的齿面上, 只有当故障轮齿在啮合位置才能产生很小的振动冲击, 所以齿轮的早期故障特征很容易被正常轮齿的振动和环境噪声所淹没。目前, 针对齿轮早期故障诊断的方法主要通过抑制噪声提高信噪比达到提取微弱特征的目的, 常用的有小波降噪[1, 2]、随机共振[3]、循环平稳解调、卡尔曼滤波[4]等多种方法。虽然这些方法在抑制噪声干扰、提高信噪比方面取得了较好的效果, 但很难有效地滤除信号中的无关周期分量, 而且在齿轮传动系统中由轴承、轴等其他旋转部件形成的周期性噪声干扰不可忽略。时域同步平均技术也称相干检波, 是旋转和往复机械故障诊断中一种非常有效的预处理方法, 可以消除随机噪声和与给定频率无关的周期信号, 提取与给定频率有关的周期分量, 能够在强噪声背景下工作, 提高分析信号的信噪比[5, 6], 而且对故障特征信号几乎没有任何削弱和抑制作用, 在齿轮、轴承等旋转机械早期故障诊断中得到了广泛应用[7]。
在实际工作过程中, 齿轮箱转速受载荷和电流的影响会存在一定的波动, 从而使等时间间隔采集到的时域信号呈现较强的非平稳特征, 特别是在升、降速阶段尤为明显, 因此直接利用传统的时频分析技术进行频谱分析往往会产生频率混叠现象, 很难准确提取到故障特征信息[8]。目前针对非平稳信号的分析处理方法很多, 常见的有短时傅里叶变换、Gabor小波变换、Winger-Ville分布和阶次分析等。而齿轮、轴承等旋转机械局部缺陷引起的故障所产生的振动特征与轴的旋转速度密切相关, 所以阶次分析技术在齿轮故障诊断应用中更具优势[9]。
针对强噪声背景下的低速斜齿轮的实际工况, 本文将角度域同步平均与阶次分析相结合, 提出了基于角度域同步平均和阶次分析的齿轮故障诊断方法, 并将其应用于低速斜齿轮点蚀故障诊断中。基于时域同步平均原理提出了角度域同步平均算法, 等角度采样可以将非平稳的时域采样信号转变为角度域里的周期平稳信号, 再对其进行同步平均可以克服时域同步平均算法对恒定转速要求的限制, 有效地抑制了随机噪声和无关周期分量的干扰, 极大地提高了信噪比。而且, 将角度域同步平均降噪与阶次分析相结合, 可以解决阶次分析不适于多分量、强噪声背景下的故障特征提取的问题。试验结果表明, 该方法可以在强噪声背景下准确地提取到低速斜齿轮早期故障振动信号特征。
基于时域同步平均的数学思想, 提出了角度域同步平均的概念。角度域同步平均是从噪声干扰中提取与给定频率(如齿轮旋转频率)相关的周期性信号的过程, 不仅可以降低系统噪声干扰, 而且可以消除与被诊断对象非同周期的周期信号。
假定角度域信号 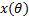
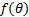
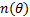
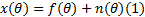
以信号 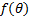
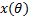
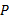
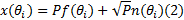
再对 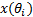
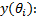
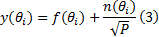
此时, 输出的白噪声信号是原来输入信号 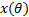
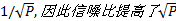
旋转机械由于局部故障引起的振动与转速密切相关, 为此产生了阶次分析技术。阶次的定义为参考轴每转内发生的循环振动次数, 阶次与对应振动频率和转速的关系可表示为[10]:
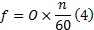
式中: 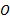
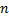
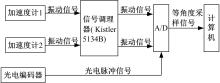
阶次分析的实质是将旋转机械在时域内的非平稳振动信号通过等角度采样转变为角度域内的平稳信号, 通过对角度域内的平稳信号进行阶次分析反映与参考轴的转速相关的振动特征。阶次分析的关键技术是实现阶次跟踪, 即等角度采样, 目前常用的阶次跟踪方法有:基于硬件式阶次跟踪技术、基于转速脉冲的阶次跟踪技术和计算阶次跟踪技术。本文所采用的是基于光电编码器的硬件式阶次跟踪, 具有实时性好、准确度高的优点。阶次分析的数据采集系统如图1所示。光电编码器安装在故障齿轮主轴末端, 并随齿轮主轴的转动而同步旋转。光电编码器内轴每转过一个相同的角度将产生一个高低相间的矩形脉冲信号, 将该信号输入到数据采集卡的外触发引脚进行外触发采样。采集卡会在光电编码器输出的矩形脉冲信号的上升沿对应时刻对加速度信号进行采样, 实现等角度采样。
设等角度采样每转采样点数为Z, 总采样点数为N, 则等角度采样间隔Δ θ =2π /Z, 所采集到的振动信号在角度域内为平稳信号, 满足离散傅里叶变换要求, 有:
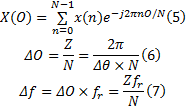
式中: 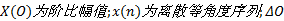
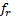
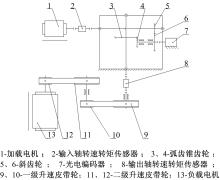
试验装置为英国诺丁汉特伦特大学先进设计制造工程中心提供的齿轮箱故障诊断测试系统, 其试验台结构简图如图2所示。试验齿轮箱由两级传动组成, 斜齿轮5(齿数为23)和6(齿数为82)构成一级传动, 弧齿锥齿轮3和4组成齿轮箱的二级传动。齿轮箱输出端有两级齿形带升速结构。其中, 带轮9和10构成一级升速, 带轮11和12为二级升速。加载电机是13, 试验台的驱动电机和负载电机通过直流母线构成一个电封闭系统。转速转矩传感器2和8可获取转速和转矩数据。其中, 转速转矩传感器2安装在高速输入轴端, 转速转矩传感器8安装在输出轴端。试验系统的加载和速度调节是以转速转矩传感器2记录的数值为基准数据进行调整。光栅编码器7安装在故障斜齿轮6的主轴端, 作为A/D板的外触发器实现等角度采样。
试验中振动测点布置如图3所示。其中, 加速度计1安装在输入轴轴承座处的齿轮箱体上, 加速度计2安装在斜齿轮8的轴承座上方的齿轮箱体上。
为验证该方法的有效性, 分别在单个齿面点蚀面积比率为30%和75%两种工况条件下进行了斜齿轮故障诊断试验研究, 如图4所示。试验中, 设定齿轮箱输入轴转速为750 r/min, 输入轴转矩为8 N/m。由于驱动电机和负载电机通过直流母线构成电封闭系统, 回路中电流的损失导致输入轴转矩在0.2 N/m范围内存在微小波动, 进而使转速也产生了微小波动。为对比不同采样方式的测试效果, 分别采用了等时间间隔采样和等角度采样两类测试方法。角度域采样频率为3600 Samples/r, 采样长度12转。时域采样频率为20 kHz, 采样时间为3.5 s。
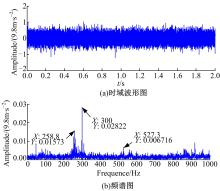
当斜齿轮单个齿面点蚀面积为30%时齿轮箱振动信号的时域波形和频谱如图5所示。图5(a)显示, 时域波形是随机信号, 不具有明显的周期性特征, 其频率成分如图5(b)所示, 存在258.8、300、527.3 Hz的峰值, 而故障特征频率成分并不突出。由图5(b)可知, 对所采集到的时域信号直接进行频谱分析很难提取到齿轮的早期故障特征。图6为单个齿面点蚀面积为30%时齿轮箱振动信号的希尔伯特包络谱图, 图中并不能清晰地显示斜齿轮的早期故障特征频率。在工程应用中, 由于齿轮箱负载变化而引起转速产生较大波动时, 其振动信号具有较强的非平稳特征, 通过传统的时频分析方法进行处理时会产生频率模糊现象, 很难对其故障情况做出准确判定。
 | 图6 30%点蚀故障振动信号希尔伯特包络谱图Fig.6 Envelop spectrum of vibration signal when the fault of helical gear is 30% pitting fault |
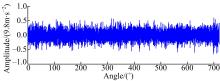
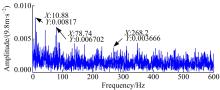
当斜齿轮单个齿面点蚀面积为30%时齿轮箱振动信号的两个周期的角度域波形如图7所示。由图7可知, 原始角度域波形不具有明显的周期性特征。图8是经过角度域同步平均处理后的角域波形, 30° 和390° 存在两个幅值较大的脉冲, 与采样周期数恰好相符。对比图7和图8不难发现, 角度域同步平均方法能够明显提高信噪比, 在不削弱故障特征信号的前提下, 极大地抑制了噪声干扰。
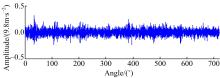 | 图8 30%点蚀故障角度域同步平均后角度域波形Fig.8 Angular domain waveform of helical gear with 30% pitting fault after angular domain synchronous average processing |
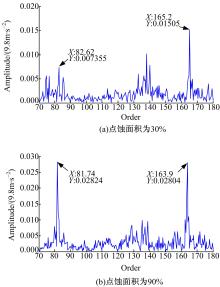
图9是齿轮无故障时齿轮箱振动信号经过角度域同步平均处理后的阶比细化谱。图10是斜齿轮单个齿面点蚀面积为30%和90%时角度域信号经过同步平均处理后的阶比细化谱。图10(a)显示, 在阶次为82.62和165.2处有清晰的峰值, 分别对应着故障齿轮1倍和2倍啮合阶次, 说明该图能够准确地反映故障齿轮的啮合情况。在图10(a)中同时存在138 Hz的峰值, 该频率处的峰值为噪声信号对应的峰值。角度域同步平均降噪效果直接取决于平均次数, 平均次数越高, 降噪效果越好, 但是随着平均次数的增加, 试验时间和数据处理计算量也随之增加, 本文中平均次数为6次, 所以不能完全消除噪声。图10(b)显示, 由于点蚀面积增加, 同一工况下在故障齿轮的啮合阶次处的峰值明显增大。由以上的分析结果可见, 图10能够如实地反映故障齿轮的啮合状态, 说明本论文所提出的方法能够准确提取到低速斜齿轮的故障特征。
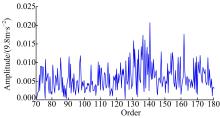 | 图9 正常齿轮角度域同步平均后阶比细化谱Fig.9 Refined angular domain waveform of helical gear without fault after angular domain synchronous average processing |
(1)斜齿轮在低速条件下运转时, 轮齿表面的局部早期故障产生的振动冲击能量较小, 故障特征不明显, 很容易被正常轮齿的振动和环境噪声所淹没。角度域同步平均方法能够有效消除随机噪声以及与给定频率无关的周期信号, 提高分析信号的信噪比。
(2)在实际工作过程中, 齿轮箱转速受载荷和电压的影响会存在一定的波动, 从而使等时间间隔采集到的时域信号呈现非平稳特征, 直接利用传统的时频分析技术进行频谱分析, 往往会产生频率混叠现象, 阶次跟踪方法通过对信号进行等角度采样在很大程度上能够消除频率混叠现象, 明显改善了分析效果。
(3)本文将角度域同步平均和阶次分析的故障诊断方法相结合, 能够有效地解决转速波动造成的频率混叠和阶次分析不适合在强噪声背景下工作的问题。试验结果表明, 该方法能够准确提取到低速旋转斜齿轮的早期故障特征。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|